Матрицалық ойындардың таза және аралас стратегиялық шешімдерін табу әдістері


Қазақстан Республикасы Білім және ғылым министрлігі
Ы. Алтынсарин атындағы Арқалық мемлекеттік
педагогикалық институты
Жаратылыстану және ақпараттандыру факультеті
Тақырыбы: Матрицалық ойындардың таза және аралас стратегиялық шешімін табу .
Орындаған: Кабдуалиева А.
Тексерген: Утельбаева А .
Арқалық 2009 ж
Үйлесімді шешімдер теориясының бір мәселелері - шешімді белгісіз шарттарда қабылдау. Шешімдердің негізделуі үшін ойындар теориясында қарастырылатын арнайы математикалық тәсілдер ойлап табу. Ойындар теориясында жас математикалық дисцеплиналар қатарына жатады. Ойынның пайда болуы 1944 жылы Нейман мен Моргенштерна «Экономикалық ұстаным және ойын теориясы » атты монографиясының жарық көруімен байланысты. Кейінірек ойын теориясы тәжірибелік маңызы бар математикалық жеке бағытқа айналып кетті.
Ойын теорииясы бұл қатысушының қалауы және мақсатты әрекетті жолмен орналасатын математикалық модельдер теориясы. Қатысушы қалауының қарама қарссы қақтығысушылар даулы жағдайға әкеліп соғады. Осындай жағдайда сипатттау қажетттілігі, өз кезегінде, мақсатты дауға қатысушының мінез құлығының рационалды ұсынысын қаратыру болып келетін ойын теориысының тууына әкеліп соқты.
Тәжірибелік даулы жағдайдың сараптамасы кезінде көптеген ұсақ факторлардың нәтижесінде пайда болатын қиындықтарды жеңу үшін жағдайын қарап моделін құрастырады. Мұндай модел ойын деп аталады. Ойынның модельде даулы жағдайы бір ережелер бойынша дамып отырады.
Ойын нәтижесінің белгісіздігі үш топқа бөлуге болады:
- Ойын ережесінің ерекшеліктері оның дамуында нәтиженің алдын ала айту мүмкіндігінің болмауы. Мұндай түрдің белгісіздігінің көзі комбинаторикалық, ал сәйкес ойындар комбинаторикалық деп аталады.
- Белгісіздіктің келесі бір көзі кездейсоқ факторлардың әсер етуші болып келеді. Барысы кезінде себептер нәтижесінде белгісіз болып келетін ойындар құмар ойындар деп аталады.
- Белгісіздіктің үшінші көзі қарсылық іс қимыл жайлы оның стратегиясы жайлы дәл мәндердің жоқтығы болып табылады. Ойынның бұл түрі стратегиялық деп аталады.
Мысал
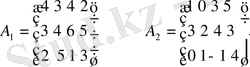
Шешімі
Осылайша
Сонымен, егер матрицаның ерлі нүктесі болса, онда ойын шешімі белгілі. Әрбір ойыншы өзінің үйлесімді стратегиясын қолданады.
Матрицалардың ерлі нүктесі жоқ ойындар шешімін табу сұрағы туындайды. Бұл ойындарда
Шарты орындалатын
Сәйкесінше В ойыншы үшін
Ойындар теориясының негізгі теориялары бар: кез келген соңғы ойынның кем дегенде бір шешімі болады және ол шешім аралас стратегия аумағынан болуы мүмкін.
Үйлесімді стратегияны пайдалану ойын құнына тең
Ойыншылардың үйлесімді стратегиясы үшін
А ойыншысының Х* оптималды стратегиясын қолдануы оның В ойыншысының қандай да іс қимылын
қатынасы тән .
Жалпы алғанда матрицаның ерлі нүктесі жоқ ойын шешімі
Қолданушы стратегиялар деп төлемді марица элементтерінің бірдей мәндері сәйкес келетін стратегияларды айтамыз. Егер
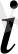 стратегиясы А ойыншы үшін негізгі деп аталады. Егер матрицаны
стратегиясы А ойыншы үшін негізгі деп аталады. Егер матрицаны
Матрицаның көлемдігін оны қатары мен бағаны бойынша бөліктер соммасы тең келетін кішкентай матрицаларға бөлу арқылы қысқартуға болады. Онда таза стратегиялар орнына матрицаға бөліктері аралас стратегиялар енгізіледі. Аралас стратегияларға сәйкес матрица бөліктері аралас стратегияға біріктірілетін таза стратегиялар санына сәйкес бөлшектер соммасын бөлу арқылы орындалады. Егер аралас стратегиялар үйлесімділер қатарына жататын болса, онда осы қатарға кіретін таза стратегиялардың қолданылу мүмкіндіктерін өзара тең.
Қатар және баған бойынша бөлшектер соммасы теңдеудің шарты орындалатын кішкентай
Алынған матрицаның ерлі нүктесі бар.
А ойыны үшін
Осылайша
- матрицаның ерлі нүктесі бар жоқтығын тексеру;
- егер ерлі нүкте болмаса, қайталанушы және негізгі стратегияларды жою үшін қатар және баған бөлшектерін өзара салыстыру;
- таза стратегиялардың белгілі бір тобын аралас стратегиялармен алмастыру үшін матрицаны кіші матрицаларға бөлу мүмкіндігін қарастыру керектігін ұмытпаған жөн.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz