Математикалық нобайлау (модельдеу) таным үрдісінде: түрлері, деңгейлері және қолдану мүмкіндіктері


УДК. 512. 2. 378
МАТЕМАТИКАЛЫҚ НОБАЙЛАУ- ТАНЫМ ҮРДІСІНДЕ
Жұмабаев Қ. Ж.,
Жұмабаев М. Ж.
Жұмыста математикалық нобайлаудың түрлері мен типтері келтірілген және олардың таным үрдісінде пайдалану мүмкіндігі көрсетілген. Мәтінді есептердің шешу алгоритмі келтірілген.
Ақпараттық-коммуникациялық технологияны пайдалану қажеттігі өмір талабынан туындап, математикалық модельдер құра алу және құрылған модель негізінде алға қойылған есепті шеше алу мүмкіндіктерін дамыту қазіргі кезеңде ерекше маңызды мәселелердің бірі болып отыр. Құбылыстар мен процестерді оқып үйренуде, өндіріс пен ғылымда есептеу техникасының кеңінен қолданылуы модельдей білу іскерлігі мен дағдыларын қалыптастыру қажеттігін туғызуда[1] . Сондықтан қазіргі кезде есептің математикалық моделін құру, яғни нобайлай алу мәселелері көкейкесті мәселелердің бірі болып табылады.
Математикалық модельдер кез-келген жүйенің құрылымдық өзгерістерін сандық түрде нақты көрсете алатындықтан ғылым мен тежірибеде кеңінен қолданылады. Мұндай модельдер білім беру жүйелерінің тиімді жұмыс істеуін бағалауда, сонымен қатар оның дамуын болжалдау мен жобалауға да қажетті. Алайда, таным процесінің мәнісі модельдеумен тығыз байланысты екеніне қарамастан олар оқу үрдісінде әлі де орнымен пайдаланыла алмай келеді.
Модель, оны нобай деп баламалап атап та жүр, шын мәнісінде, кез-келген кәсіптік танымдық жүйе, үрдіс немесе құбылысты танудың басты әмбебап ұғымы.
Модель мен модельдеу - нақты мәселеден (есептен ) оның шешішіне апаратын негізгі ұстын (көпір) . Математикалық модель модельденуші жүйенің құрылымы мен ішкі логикасына бойлап енуге мүмкіндік береді.
Модель -обьект немесе обьектінің сипаттамасы, басқаша айтқанда белгілі бір жүйені оның қандайда бір қасиеттерін зерттеу үшін басқа жүйемен алмастыру. Кез-келген модель белгілі бір гипотезалар, шарттылықтар негізінде құрылады. Обьектіні матетатикалық жүйемен көрсете отырып, обьектінің математикалық моделін аламыз. Модельдер нысанына қарай танымдық, прагматикалық және құралдық болып табылады.
Танымдық модель - білімді үйлестіру мен таныту, ескі мен жаңа білімді ұштастыру құралы. Ол, әдетте шындыққа лайықталған теориялық модель.
Прагматикалық модель - нақты іс-әрекеттерді ұйымдастыру тәсілі, жүйені басқару үшін мақсаттарды айқындау. Шындық қандай да бір прагматикалық модельге лайықталады. Прагматикалық модель қолданбалы болып табылады.
Құралдық модель - танымдық немесе прагматикалық модельдерді құру, зерттеу және пайдалану тәсілі.
Танымдық модельдер ақиқаттағы болмысты көрсетсе, ал прагматикалық, ақиқатта болмаса да қажетті, орындалуы мүмкін қатынастар мен байланыстарды танытады.
Модельдеу деңгейіне қарай:
-эмпирикалық - эмпирикалық фактілер, бағыныштылықтар негізінде ;
-теориялық - математикалық сипаттау негізінде ;
-аралас, жартылай эмпирикалық- эмпирикалық бағыныштылық пен математикалық сипаттаудан құралған болуы мүмкін;
Модельдеу (нобайлау) мәселесі үш сатыдан тұрады :
- Модельді құру (бұл саты модель құрудың нақты алгоритмі болмағандықтан, мейлінше формальдығының төмендігімен сипатталады) .
- Модельді зерттеу (бұл саты формальданған, әртүрлі модельдерді зерттеу әдістері бар) .
- Модельді қолдану (құрылымдылығымен қатар нақтылығымен сипатталады ) .
Қазіргі кезде ғылыми және педагогикалық зерттеулер жүргізуде, яғни зерттеу объектілерін оқып үйренуде, оларды біліп тану үрдісінде математикалық модельдерді қолданудың ролі артып отыр[2] . Табиғаттағы шындық процестердің сызықтық емес жүйелерін модельдеу арқылы ақиқатты тану, таным үрдісінің кеңеюіне және білім берудің артуына мүмкіндік береді.
Модельдеудің негізгі типтерін келтірейік :
Статикалық модель . Статикалық модельде уақыт мөлшері қолданылмайды. Ол уақыттың әрбір үздігіндегі қалыпты көрсетеді. Мысалы, Ньютонның екінші заңы Ғ=ma. Бұл заң салмағы m болатын материалдық нүктенің а үдеуімен қозғалысының статикалық моделі. Бұл модель уақыт өлшеміне тәуелсіз.
Динамикалық модель . Бұл модельде параметрлер арасында уақыт өлшемі есептеледі. Мысалы, S=gt 2 / 2 формуласы дененің еркін түсуіндегі жолының динамикалық моделі.
Дискреттік модель . Бұл модельде уақыттың дискретті сәттеріндегі зерттелінетін құбылыстың сипаттамасы көрсетіледі. Мысалы, S=gt 2 / 2 формуласымен t=0, 1, 2, …, 10 (сек) уақыттарындағы жолдарды есептесек, онда S 0 =0, S 1 =g/2, S 2 =2g, …, S 10 =50g моделі, мәндері алынады. Демек, t=0, 1, 2, …, 10 (сек ) мәндерінде S t =gt 2 /2 моделі, S 0 =0, S 1 =g/2, S 2 =2g, …, S 10 =50g сандық реттілігі, дененің еркін құлауының дискреттік моделі болып табылады.
Үздіксіз модель . Бұл модель белгілі бір уақыт аралығындағы уақыттың барлық сәттеріндегі жүйенің өзгеруін сипаттайды. Мысалы, S=gt 2 / 2, 0<t<100 моделі (0; 100) уақыт аралығында үздіксіз модель болып табылады.
Имитациялық модель . Бұл модельде, ондағы бірнеше немесе барлық параметрлерін өзгерту арқылы обьтектінің даму мүмкіндіктерін зерттейді немесе сынайды. Мысалы, кәсіпорында екі түрлі тауар (1және2), х 1 және х 2 көлемінде өндірілсін. Ал а 1 және а 2 тауар бірлігінің құны болса, онда тауардың жалпы құны S= a 1 x 1 +a 2 x 2 қатысы түрінде сипатталады. Мұндағы S-кәсіпорын өндірген барлық өнімнің жалпы құны. Бұл модеьді S жалпы құнды өндірілетін тауар көлемі мәнінің қалайда өзгеруіне байланысты айқындауға болатын имитациялық модель деп атауға болады.
Детерминантты модельде әрбір алғашқы параметрлер жиынтығында белгілі бір анықталған параметрлер қайталанып келіп отырады. Егер олай болмаса модель детерминантты емес, яғни стохастикалық (кездейсоқтық) деп аталады. Жоғарыда келтірілген модельдер детерминантты. Егер S=gt 2 / 2, 0<t<100 моделінде жел екпіні р-кездейсоқтық параметрін ескерсек, онда S(p) =g(p) t 2 /2, 0<t<100 құлаудың стохастикалық моделі болып табылады.
Теориялық- жиындық моделі қандай да бір жиын мен оның элементтері арасындағы қатыстылық арқылы өрнектеледі. Мысалы, X={Мұхтар, Мұрат, Айнұр, Гүлнұр, Сәкен, Шоқан} жиыны мен Мұхтар - Айнұрдың жолдасы, Гүлнұр -Мұраттың жұбайы, Сәкен- Мұхтар мен Айнұрдың баласы, Шоқан- Гүлнұр мен Мұраттың баласы, Мұхтар мен Мұраттың отбасылары бір- бірімен достық қатынаста берілсін. Онда у жиыны мен санамаланған у қатынастары екі дос отбасының теориялық- жиындық моделі ретінде қолданыла алады.
Логикалық модель предикаттармен, логикалық функциялармен өрнектеледі. Мысалы, z= x ^ y ^ x ^ y, p = x ^ y екі логикалық түрдегі функция жиыны бір разрядтты қосқыштардың математикалық моделі ретінде қолданыла алады.
Ойын моделі . Ойынға қатысушылар (жеке тұлғалар, каолициялар) арасындағы белгілі бір ойын ситуацияларын суреттейді.
Алгоритмдік модель дамуды, функциялауды айқындайтын қандай да бір алгоритм немесе алгоритмдер кешені.
Тілдік, лингвистикалық модель формальді тілдік жүйе немесе құрылым арқылы беріледі. Оларды кейде вербальді, синтаксистік және т. б. деп те атай береді. Мысалы, жол жүру ережелері- көлік пен жаяу адамдардың жолда қозғалуының тілдік, құрылымдық моделі.
Геометриялық модель геометриялық бейнелер мен обьектлер арқылы беріледі. Мысалы, түзу сызық- сандық ось моделі.
Моделдердің бұдан бөлек визуальды натурлық, клеткалық-автоматтық, фрактальді (мысалы, контур жиынтығы) типтері бар.
Модель латын сөзі, аудармасы «өлшем, мөлшер» деген мағынаны білдіреді. Математикалық модельдеу дегенде біз табиғатпен қоғамда болып жатқан құбылыстардың, яғни зерттеліп отырған процестердің математикалық теңдеулер мен теңсіздіктер немесе математикалық формулалар арқылы өрнектеледі деп түсінеміз. Қандай да бір құбылыстың «математикалық моделі» құрылды дегенде сол құбылыстың өту процесі математикалық тілде жазылды деп түсініледі. Мысалы, ғарыштық кемелердің кеңістікте белгілі бір сызық -орбита бойынша ұшуын математикалық модельдеу арқылы есептер шығарған, математикалық модельде қолданбалы есептерді шешудегі негізгі құрал болып табылады. Сондай-ақ, экономикалық есептердің моделдерін құру арқылы олардың тиімді шешімдерін анықтайды.
Табиғат тану ілімдерінің көптеген мәселелері математикалық нобайлаудың көмегімен шешіледі. Физиканың, геометрияның және механиканың т. б. ғылымдар саласында көптеген есептерді шешу дифференциалдық теңдеулерге келтіріледі. Дифференциал теңдеулер оңайлықпен құрыла бермейді. Дифференциал теңдеулерді құрудың әмбебап әдісі жоқ. Дифференциалдық теңдеулерді құруда туындының геометриялық және механикалық мағыналары пайдаланылады. Мысалы, қисыққа жанама жүргізу есебі т. б. [3, 4] . Мынандай есеп қарастырайық. Екі стакан кофе бар. Кофеге сүтті құйып 10 минут жауып қойғанмен, 10 минутта жауып қойып содан кейін сүтті құйған жағдайлардың қайсысында кофе ыстығырақ болады? деген есепті қарастырайық. Мұнда екі жағдайда да стаканның бетін жауып қоюдың уақыттары бірдей. Физикалық заңдылықтарды, ондағы тұрақтылық коэффиценттерін ескере отырып, дифференциал теңдеу құруға болады, яғни есептің математикалық нобайын жасайды. Нәтижесінде дифференциалдық теңдеу алынады. Алынған дифференциалдық теңдеуді шешіп, жылу өткізгіштік коэффиценттерді т. б. физикалық тұрақтыларды және температураны ескеру арқылы есептеу жүргізгенде алдымен жауып қойып, 10 минуттан соң сүт құйылған кофе ыстығырақ болатындығы алынады [4] .
Математикалық модельдеу биологияда, химияда, экологияда, астрономияда, медицинада және әскери ғылымдарда да кеңінген қолданылады. Салмақсыздық туралы есепті матеамтикалық нобайлау арқылы шешеді. Жерді айналып жүрген космос кораблінің жылдамдығы
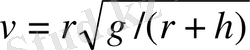 болғанда кабина ішіндегі адам салмақсыздық жағдайда болады екен. Мұнда r-жердің радиусы, h-корабльдің жер бетінен ұшу қашықтығы, g-жер бетіндегі ауырлық күшінің үдеуі. Космосқа кеңістік кемелерін ұшырар алдында, оның ұшу траекториясын, жерден көтерілу орбитасын, егер жерге қайтадан оралатын болса, оның қону мүмкіндіктерінің есебі математикалық нобайлау арқылы жүзеге асырылады.
болғанда кабина ішіндегі адам салмақсыздық жағдайда болады екен. Мұнда r-жердің радиусы, h-корабльдің жер бетінен ұшу қашықтығы, g-жер бетіндегі ауырлық күшінің үдеуі. Космосқа кеңістік кемелерін ұшырар алдында, оның ұшу траекториясын, жерден көтерілу орбитасын, егер жерге қайтадан оралатын болса, оның қону мүмкіндіктерінің есебі математикалық нобайлау арқылы жүзеге асырылады.
Мектеп бағдарламасында да математика, физика, химия, т. б. пәндернде есептерді шешуде модельдеу процесі кеңінен қолданылады[5] . . Математика курсында мәтінді есептерді алгебралық әдіспен шешу математикалық модельді пайдаланудың бір түрі болып табылады. Мәтінді есептерді шешу мынандай сатылардан тұрады:
1. Есептің шарты бойынша ізделінді шамаларды белгісіздермен белгілеу.
2. Белгісіз шамалар мен берілген шамалар арасындағы байланыстарды табу, яғни теңдеулер мен теңсіздіктерді жазу.
3. Мәселедегі шамалар мен ізделінетін белгісіздердің қандай математикалық шарттарды қанағаттандыратынын анықтау.
4. Құрылған теңдеулер мен теңсіздіктер шешулерінің қойылған мәселенің мазмұнына толық сәйкес келетіндігін анықтау.
Келтірілген екінші сатыда есептің математикалық теңдеуі жазылады, ал үшінші сатыда қателікті анықтау мүмкіндігі жүзеге асырылады. Төртінші саты құрылған модельдің қойылған есептегі мәселеге сәйкес келуін, яғни мәселенің және мазмұнның модельде толық қамтылғандығын анықтауға мүмкіндік береді. Математикалық модельдер және модельдеу көптеген есептерді шешіп, олардың қолдану аясын анықтауға мүмкіндік береді.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz