Әдістің бірінші нұсқасы

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 3 бет
Таңдаулыға:

Лаграндждын кобейткиш адиси

Әдіс негізгі 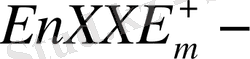де 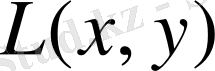Лаграндж функциясының ерлі нүктесін 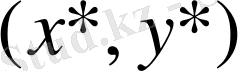табуды. Интеграциялық процестер құру .

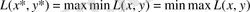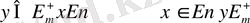
қатынасына сүйенеді.

Әдістің бірінші нұсқасы. Бұл Эрроу мен Гурвиц ұсынған әдістің мәні 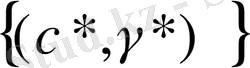іргелерінің

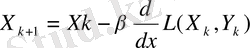
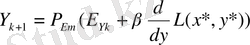
формуласы бойынша құруда

дегі V нүктесінің проекциясын білдіреді.

Осылайша, 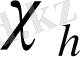нүктелері х ауыспалысы бойынша 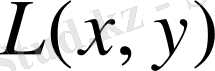формуласының шартсыз азаюы мәселесін шешу үшін градиентті төмендеу әдісімен құрылса, 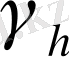нүктелері = 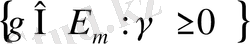көбейтіндісінің у ауыспалысы бойынша <(x, y) функциясының өсу мәселесін шешу үшін градиент проекциясы әдісімен құрылады.

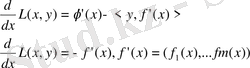
болғандықтан, көрсетілген процесс қарапайымдылығымен көзге түседі, ал тегі жобалау бөлшекті түрде жүзеге асырылады.

Өкінішке орай, бұл әдіс градиенттік төмендеу әдісі сияқты, градиент проекциясы әдісінің де ұқсастығын кепілдік берілген жағдайда да талап етілген ұқсастық пен қамтамасыз ете алмайды.

Бұған 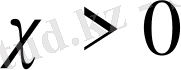оң таңбалы жартылай осіндегі біркелкі төмендеу мәселесінің танымал бөлшекті мысалы куә.

Әдістің екінші нұсқасы. Бұл нұсқа алдыңғыдан әрбір интеграция кезінде 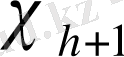кезекті нүктесін 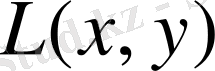функциясының х ауыспалысы бойынша толығымен төмендеуі нәтижесінде алу ұсынысымен ерекшеленгенде:

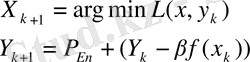
Бұл нұсқада ұқсастың градиент проекциясы ұқсастығы туралы 10. 2. 5., 10. 2. 6 теоремалар дәлелденген шарттарда орын алды.

Соңғы он жылда Лагранж модификацияланған функцияларын құру кезінде жасалған математикалық бағдарламаудың мәселе шешудің сандық әдіске арналған жұмыстары көбейді.

Лагранждық модификацияланған функция әдісі Лагранж көбейткіштері әдісі қолданудың кеңінен таратуға мүмкіндік береді және өзінің мақсаты ретінде ерлі нүкте іздеудің есептеу барысының өнімділіг арттыруыды қарастырады.

Лагранждық модификацияланған функцияларын құру келесі көзқарастарымен негізделеді.

ф(х) функциясының төмендеу мәселесі үшін әлдебір х көбейтіндісінде E _n+m кеңістігінде анықталған 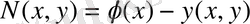функциясын құрамыз.

Мақсатты қарап шығып ерекше функцияларға арналған бірнеше өзгергіштердің экстремумі ізделінеді бірақ барлық анық облыстары жол ал жиында қанағаттандырғанда - Функция шартқа 2= f ( x, y ) х дәлелдері және қайсының g шартына( х, ) =, қанағаттандырады шешіміне байланысты аталады.

Анықтама . Егер нүкте минимумның g шартына (х ) =, не барлық нүктелердің артынан ( х, ) орындалатын теңдік. ( x 0, шартты нүктемен 0) аталады .

Экстремен шартты табу қарапайым тәсілімен ең функция сумасы екінің өзгергіштердің функция экстремум біреуін өзгергіштің G байланыстары теңдеу мүмкін береді.

Жалпы оқиғасында шартты экстремум іздеп табуына арналған Лагранжа . көбейткіштерінің әдісі үшеудің функцияны қарап шығамыз өзгергіштердің ( x, y, ) = f ( x, y +) [ g ( x, y ) - C ] .

Мынау функция Лагранж функциясымен аталады.

Теорема . Егер нүкте ( xо, уо ) z функциялары шартты экстремум нүктесімен келеді = f ( х, ) g шарты жанында ( х, ) =, онда функциялары экстремум нүктесімен келеді сондай мағына, нүкте бар болады ( x, y, ) .

Сайып келгенде, функция шартты экстремумі табуына арналған шарт жанында жүйе шешімін табуы

Оқиғада, егер сан өзгергіштердің көбірек екінің, жасай алады және байланыс бірнеше теңдеуінің . Сәйкесті мына оқиғада болады және Лагранж бірнеше көбейткішінің шартты экстремум жеткілікті шарттары осында анықтап қарамаймыз . Тек қана белгілеп қоямыз, не көптегендерді жалғыз мақсаттарда Лагранж функция сын нүктесі болады және тек қана емес жергіліктіге, сонымен қатар шарттыға немесе барынша толыққа айналады.

Сондай экономикалық мақсаттардың шешімі жанында шартты экстремум табу мақсаты қолданылады, табу сияқты қорлардың тарату құнды қағаздардың үйлесімді таңдау және т. б.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.