Қисық сызықты қозғалыс: жанамалық жылдамдық, қисықтық радиусы және үдеудің нормальдық пен тангенциалдық құрамалары


 Қисық сызықты қозғалыс.
Қисық сызықты қозғалыс.
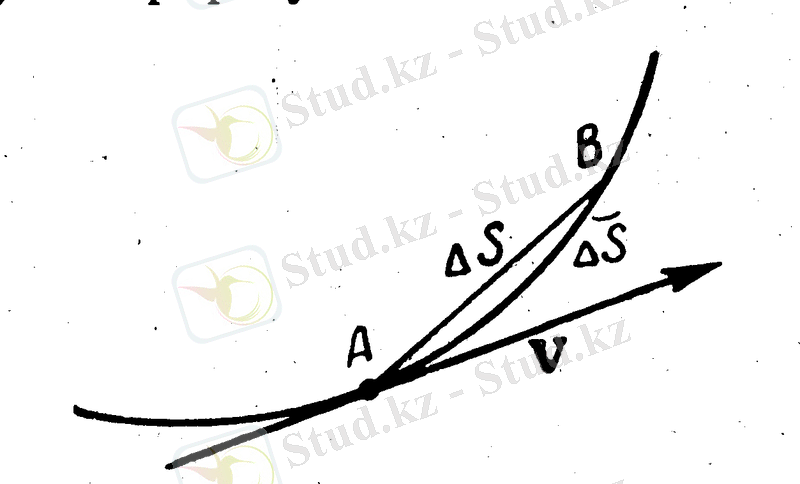
Егер материялық нүкте қозғалғанда ашылатын сызық, яғни оның траекториясы қисық сызық болып келсе, оңда қозғалыс қисық сызықты қозғалыс деп аталады. Қисық сызықты қозрғалыс кезіндегі жылдамдық векторын анықтау үшін бір аз уақыт аралығын алып қарастырайық; осы аз уақыт аралығында материялық нүкте азғаңа доғалық жол Аз жүреді. Егер біз уақыт аралығын шексіз азайта берсек, онда А5 доғасы шексіз кішірейе береді де, өзінің шегінде, оны керіп тұрған А5 хордасымен беттесіп кетеді. Қисық Сызықты қозғалыс ақырында шексіз кішкене участокта түзу сызықты қозғалыспен дәл келеді. Сондықтан қисық сызықты қозғалыстың берілген А нүктесіндегі жылдамдығының сан мәні мынаған тең болады:
және
 шамаларының араларында мынадай байланыс бар екендігі мәлім:
шамаларының араларында мынадай байланыс бар екендігі мәлім:

 Жазық сызықтың бір
А
нүктесіндегі
қисықтық дөңгелек
деп, Ш нүктесі мен оған шексіз жақындатылған В және В
2
нүктелерінен өтетін шеңбердің шектік орнын айтады (1-суретте қисық тұтас сызы С-пен, қисықтық дөңгелегі үздік-үздік сызықпен сызылған) . Қисықтық дөнгелегінің радиусы қарастырып отырған қисықтың А нүктесіндегі
қисықтың радиусы,
ал сол дөңгелектің центрі осы
А
нүктесі үшін қисық сызықтың
қисықтығының центрі
болады.
Жазық сызықтың бір
А
нүктесіндегі
қисықтық дөңгелек
деп, Ш нүктесі мен оған шексіз жақындатылған В және В
2
нүктелерінен өтетін шеңбердің шектік орнын айтады (1-суретте қисық тұтас сызы С-пен, қисықтық дөңгелегі үздік-үздік сызықпен сызылған) . Қисықтық дөнгелегінің радиусы қарастырып отырған қисықтың А нүктесіндегі
қисықтың радиусы,
ал сол дөңгелектің центрі осы
А
нүктесі үшін қисық сызықтың
қисықтығының центрі
болады.
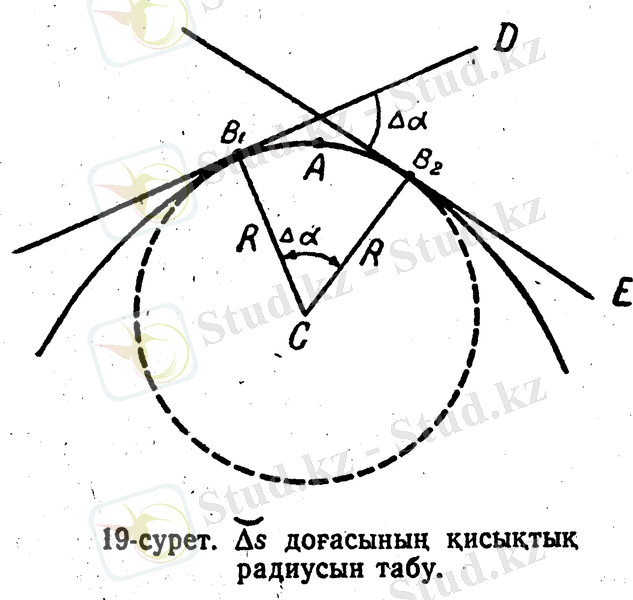
В
1
А және В
2
нүктелерінен өтетін шеңбердің В
1
және В
2
нүктелерін бастыра
В
1
D
және В
2
D жанамаларын жүргізейік. Осы жанамаларға түсірілген В
1
С және В
2
С нормальдары шеңбердің радиустары болады да, сол шеңбердің С дентрінде қиылысады. В
1
С және В
2
С нормальдарының арасындағы бұрышты
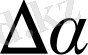 деп белгілейік; ол, әрине, В
1
D және В
2
С жанамаларының арасындағы бұрышқа тең болады. (2) формула бойынша:
деп белгілейік; ол, әрине, В
1
D және В
2
С жанамаларының арасындағы бұрышқа тең болады. (2) формула бойынша:
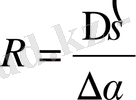 ,
,
мұнда
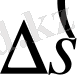 арқылы
арқылы
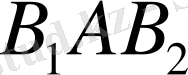 дөңгелеік доғасы белгіленген. Егер
дөңгелеік доғасы белгіленген. Егер
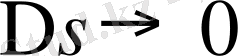 болса, онда жоғарыда айтылғандай, шеңбердің радиусы қисықтың
А
нүктесіндегі қисықтық радиусын береді. Сонымен, қисықтың қисықтық радиусы мынаған тең:
болса, онда жоғарыда айтылғандай, шеңбердің радиусы қисықтың
А
нүктесіндегі қисықтық радиусын береді. Сонымен, қисықтың қисықтық радиусы мынаған тең:
Ал R-дің кері шамасы сызықтық берілген нүктедегі қисықтығы болады:
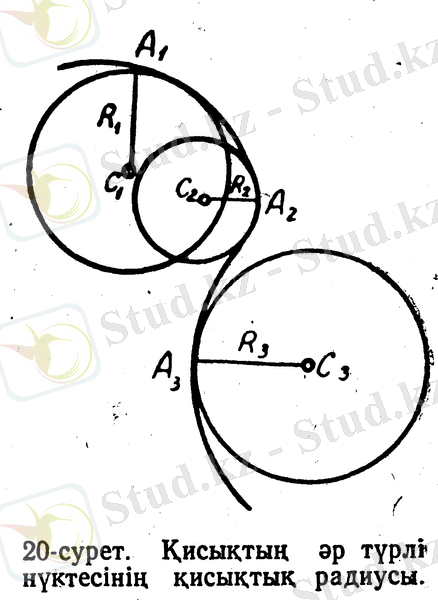
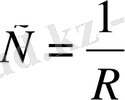
20-суреттен қисық жазыңқы болып келген А 1 нүктесіндегі қисықтық радиусының ұзын, ал қисық көбірек иілген А 2 нүктесіндегі қисықтық радиусы R 2 - қысқа екендігі көрініп тұр. Қисықтың А 1 мен А 2 нүктелеріндегімен салыстырғанда дөңесі басқа жаққа қарап кеткен А 3 нүктеде қисықтық центрі де қисықтың екінші жағында жатыр.
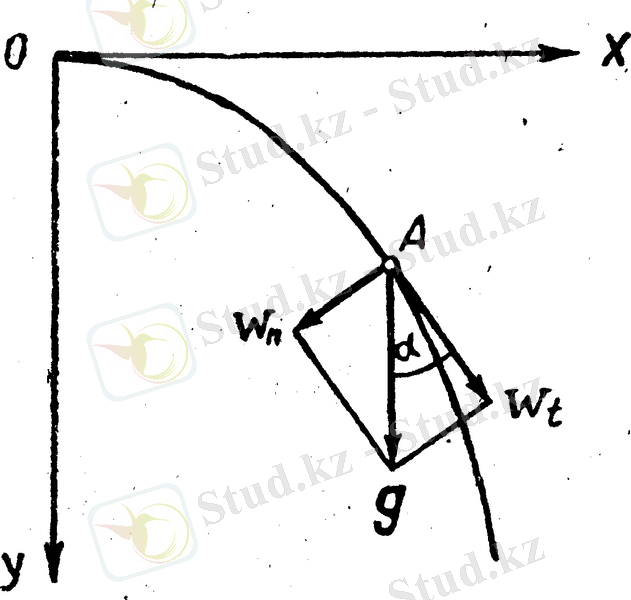
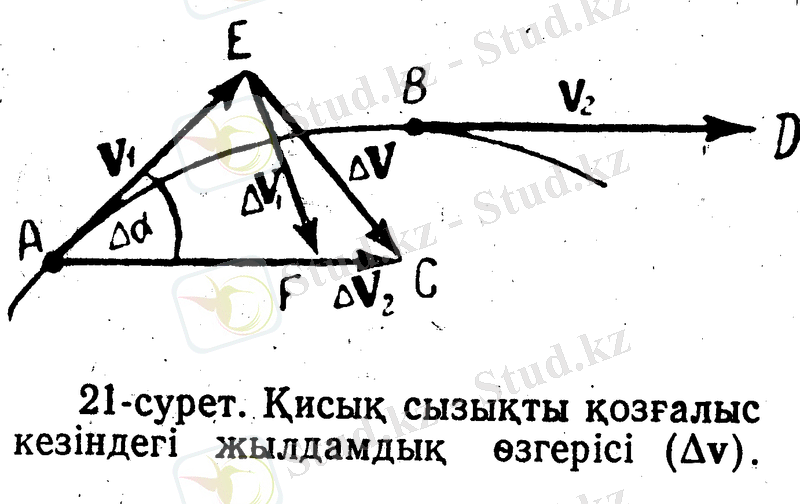 Енді жазық қисық бойымен бір қалыпты қозғалмаған дененің үдеуіне толығырақ тоқталайық. Қисықтың
А
нүктесіндегі жылдамдық векторы
v
1
,
В
нүктесіндегі жылдамдық векторы болсын (21-сурет) . векторының шамасын да, болғанда да
v
1
векторынан басқа.
А
нүктесінен бастап
АС
кесіндісін жүргізейік, ол векторын кескіндейтін
ВD
кесіндісіне әрі тең, әрі параллель болсын. Сонда мен
v
1
векторларының айырмасына тең
ЕС
кесіндісі
АВ
жолының бойындағы жылдамдықтың
Енді жазық қисық бойымен бір қалыпты қозғалмаған дененің үдеуіне толығырақ тоқталайық. Қисықтың
А
нүктесіндегі жылдамдық векторы
v
1
,
В
нүктесіндегі жылдамдық векторы болсын (21-сурет) . векторының шамасын да, болғанда да
v
1
векторынан басқа.
А
нүктесінен бастап
АС
кесіндісін жүргізейік, ол векторын кескіндейтін
ВD
кесіндісіне әрі тең, әрі параллель болсын. Сонда мен
v
1
векторларының айырмасына тең
ЕС
кесіндісі
АВ
жолының бойындағы жылдамдықтың
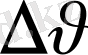 өзгерісін көрсетеді.
В
нүктесің
А
нүктесіне жақындата берсек, дененің А нүктесінен
В
нүктесіне баруына кететін
өзгерісін көрсетеді.
В
нүктесің
А
нүктесіне жақындата берсек, дененің А нүктесінен
В
нүктесіне баруына кететін
 уақыт аралығы да нольге ұмтылатын болады. Сонда формула бойынша
А
нүктесіндегі үдеудің өрнегі табамыз:
уақыт аралығы да нольге ұмтылатын болады. Сонда формула бойынша
А
нүктесіндегі үдеудің өрнегі табамыз:
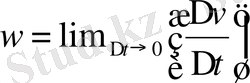
АС-нің бойымен АF=v
1
кесіндісін салайық және
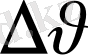 -ні
-ні
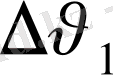 және
және
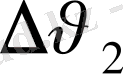 құраушыларына жіктейік. Сонда
құраушыларына жіктейік. Сонда
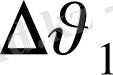 жылдамдықтың бағыты жағынан өзгергенін,
жылдамдықтың бағыты жағынан өзгергенін,
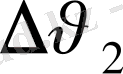 жылдамдықтың шама жағынан өзгергенін сипаттайды,
жылдамдықтың шама жағынан өзгергенін сипаттайды,
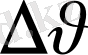 =
=
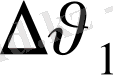 +
+
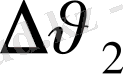 ал болады; енді
ал болады; енді
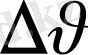 -нің осы мәнін
w
үдеуінің өрнегіне қойсақ, мынау шығады:
-нің осы мәнін
w
үдеуінің өрнегіне қойсақ, мынау шығады:
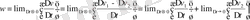 .
.
Мұндағы қосудың бәрі векторлық қосу. Мына шама
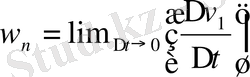
жылдамдықтың тек бағыты жағынан өзгергенін сипаттайтын үдеудің құраушысы болады.
АЕ
мен
АС
арасындағы бұрышты
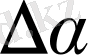 деп белгілейік; салу бойынша бұл
v
1
мен
v
2
жылдамдықтарының арасындағы бұрыш, ендеше ол қисықтың
А
және
В
нүктелерінде жүргізілген жанамалардың арасындағы бұрыш болады. 21-суреттен
деп белгілейік; салу бойынша бұл
v
1
мен
v
2
жылдамдықтарының арасындағы бұрыш, ендеше ол қисықтың
А
және
В
нүктелерінде жүргізілген жанамалардың арасындағы бұрыш болады. 21-суреттен
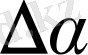 бұрышы кішкене болғанда былай жазуға болатынын көреміз:
бұрышы кішкене болғанда былай жазуға болатынын көреміз:
ЕF=АЕ-
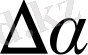 Equation. 3
,
Equation. 3
,
ал
ЕF=
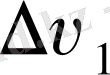 Equation. 3 AЕ =
Equation. 3 AЕ =
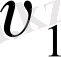 Equation. 3, ендеше
Equation. 3, ендеше
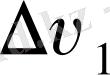 Equation. 3 =
Equation. 3 =
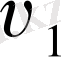 Equation. 3
Equation. 3
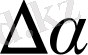
Осы өрнегін пайдалана отырып, (3) формула бойынша үдеудің құраушысының сан мәнін табамыз:
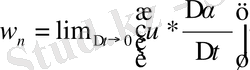 .
.
Шек белгісінен соңғы шаманы
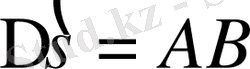 доғасының ұзындығына көбейтеміз және бөлеміз; сонымен қатар t > 0 болса,
доғасының ұзындығына көбейтеміз және бөлеміз; сонымен қатар t > 0 болса,
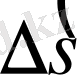
 ескеріп, осы өрнектерді пайдаланып,
w
п
мәнін табамыз:
ескеріп, осы өрнектерді пайдаланып,
w
п
мәнін табамыз:
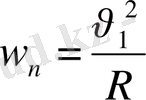 ,
,
мұндағы
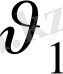 - дененің
А
нүктесіндегі жылдамдығы, R- қисықтың сол нүктедегі қисықтық радиусы. Ең ақырында,
- дененің
А
нүктесіндегі жылдамдығы, R- қисықтың сол нүктедегі қисықтық радиусы. Ең ақырында,
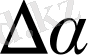 - 0 болса,
АЕF
- 0 болса,
АЕF
 90°, олай болса
90°, олай болса
 векторы қисықтық
А
нүктесінен жүргізілген жанама бойымен бағытталған
векторы қисықтық
А
нүктесінен жүргізілген жанама бойымен бағытталған
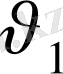 жылдамдығына нормаль болады. Сонымен, бағыты жағынан -
жылдамдығына нормаль болады. Сонымен, бағыты жағынан -
 - мен дәл келетін үдеуі жылдамдыққа нормаль (перпендикуляр) болып орналасады және берілген нүктеде қисықтық центріне қарай бағытталады екен. Осыған сәйкес толық үдеудің w
n
бөлігі
нормаль үдеу
немесе
центрге тартқыш үдеу
деп аталады. Осы айтылғандардан үдеудің екінші бөлігінің де бағытын опоңай анықтай аламыз; шындығында, егер
- мен дәл келетін үдеуі жылдамдыққа нормаль (перпендикуляр) болып орналасады және берілген нүктеде қисықтық центріне қарай бағытталады екен. Осыған сәйкес толық үдеудің w
n
бөлігі
нормаль үдеу
немесе
центрге тартқыш үдеу
деп аталады. Осы айтылғандардан үдеудің екінші бөлігінің де бағытын опоңай анықтай аламыз; шындығында, егер
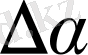
 0 болса,
АС
кесіндісі бағыты жағынан
v
1
-ге жуықтайды; олай болғанда
0 болса,
АС
кесіндісі бағыты жағынан
v
1
-ге жуықтайды; олай болғанда
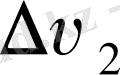 Equation. 3, сондықтан w
t
де,
v
1
жылдамдығы бағытталған түзудің бойымен, яғни қисықтың
А
нүктесінде жүргізілген жанаманың бойымен бағытталады. Соңдықтан үдеудің w
t
бөлігі
жанамалық
немесе
тангенциал үдеу
деп аталады.
Equation. 3, сондықтан w
t
де,
v
1
жылдамдығы бағытталған түзудің бойымен, яғни қисықтың
А
нүктесінде жүргізілген жанаманың бойымен бағытталады. Соңдықтан үдеудің w
t
бөлігі
жанамалық
немесе
тангенциал үдеу
деп аталады.
Қорыта келгенде былай деуге болады: қисық сызықты қозғалыстың толық v i үдеуін құраушы екі үдеуге:
1) жылдамдықтық шама жағынан өзгеруін сипаттайтын тангенциал үдеуге,
2) жылдамдықтыц бағыты жағынан өзгеруін сипаттайтын нормаль үдеугз жіктеуге болады. Сонда
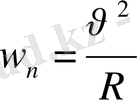
мұндағы R- траекторияның берілген нүктедегі қисықтық радиусы. v - дененің сол нүктедегі жылдамдығының мәні; нормаль үдеу қисыққа түсірілген нормаль бойымен (қисықтық центріне қарай) бағытталады.
Тангенциал үдеу:
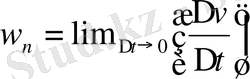 ,
,
мұндағы
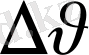 - жылдамдық векторынын сан мәнінің өзгерісі; тангенциал үдеу қисыққа жүргізілген жанама бойымен бағытталады. Әрине, нормаль үдеу w
n
мен тангенциал үдеу w
t
тангенциал үдеу өз ара
перпендикуляр
болады. Сондықтан w толық үдеудің сан мәні мынаған тең:
- жылдамдық векторынын сан мәнінің өзгерісі; тангенциал үдеу қисыққа жүргізілген жанама бойымен бағытталады. Әрине, нормаль үдеу w
n
мен тангенциал үдеу w
t
тангенциал үдеу өз ара
перпендикуляр
болады. Сондықтан w толық үдеудің сан мәні мынаған тең:
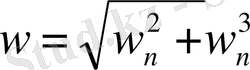 .
.
Толық w үдеуі векторының бағыты не w мен қисықтық радиусы арасындағы
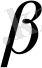 бұрышы арқылы, не w мен жанама арасындағы
бұрышы арқылы, не w мен жанама арасындағы
 бұрышы арқылы анықталады:
бұрышы арқылы анықталады:
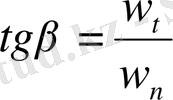 ,
,
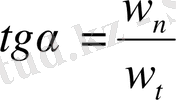
Дене қисық бойымен бір қалыпты қозғалғанда w t = 0 және w=w n сонымен, бір қалыпты қисық сызықты қозғалыста тангенциал үдеу нольге тең, ал толық үдеу нормаль үдеумен дәл келеді және траекторияның әрбір нүктесінде траекторияға жургізілген нормальдің бойымен қисықтық центріне қарай бағытталады. Бұдан, осы жағдайда жылдамдық шама жағынан тұрақты бола тұрса да, оның бағыты ұдайы өзгеріп отыратындығы көрінеді.
Осы шығарылған формулалар жазық қисық бойымен болған қозғалысқа жатады, бірақ талдап қорыта келіп, оларды жазық емес қисық бойымен болған қозғалысқа да қолдануға болады.
Табиғатта да, техникада да траекториялары түзу сызық емес, қисық сызық болып келетін қозғалыстар өте жиі кездеседі. Бұл қисық сызықты қозғалыстар. Планеталар мен Жердің жасанды серіктері - ғарыш кеңістігінде, ал Жер бетінде - барлык, транспорттар, машиналар мен механизмдердің бөлшектері, өзен сулары, атмосферадағы ауа және с. с. қисық сызықты траекториямен қозғалады.
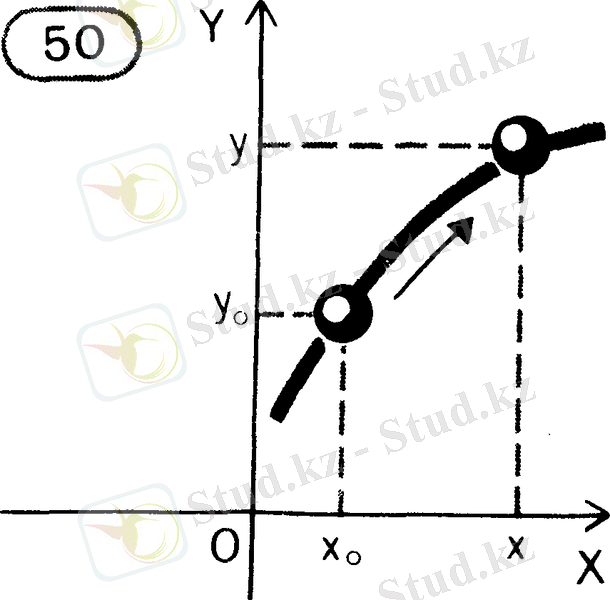
Қисық сызықты қозғалыс түзу сызықты қозғалыстан гөрі күрделірек. Мұндай қозғалыста дененің тек бір ғана координаты өзгереді деуге болмайды. Мысалы, егер қозғалыс жазықтықта болса, онда 50-суреттен көріп отырғанымыздай, қозғалыс кезінде екі координат: х пен у өзгереді. Қозғалыс бағыты, яғни жылдамдық векторының, демек, үдеу векторының бағыты үнемі өзгеріп отырады. Жылдамдық пен үдеудің модульдері өзгере алады. Осының барлығы қисық сызықты қозғалыстың түзу сызықты қозғалыстан гөрі күрделі екендігін көрсетеді.
ҚИСЫҚ СЫЗЫҚТЫ ҚОЗҒАЛЫС КЕЗІНДЕГІ ОРЫН АУЫСТЫРУ ЖӘНЕ ЖЫЛДАМДЫҚ
Түзу сызықты козғалыс кезінде жылдамдық векторының бағыты әрқашан да орын ауыстыру векторымен бағыттас болады. Қисық сызықты козғалыс кезіндегі жылдамдық пен орын ауыстырудың бағыттары туралы не айтуға болады?
Хорда бойымен орын ауыстыру. қайсыбір қисық сызыкты траектория берілген. Дене осы траекторияның А нүктесінен В нүктесіне қарай қозғалады дейік. Сонда дененің жүріп өткен жолы- АВ доғасының ұзындығы, ал оның орын ауыстыруы - АВ хордасы бойымен бағытталған вектор.
Енді біз жылдамдық әрдайым орын ауыстыру векторы бойымен бағытталады деп айта алмаймыз. А мен В нүктелерінің арасынан бІрнеше хордалар жүргізейік және дене осы хордалар бойымен козғалады деп есептейміз. Олардың әрқайсысында дене түзу сызықты қозғалады және жылдамдық векторы хорданың, яғни орын ауыстыру векторының бойымен бағытталады.
Лездік жылдамдық жанама бойымен бағытталады. Енді түзу сызықты бөліктерді әлдеқайда қысқарақ етіп алайық. Олардың әрқайсысында жылдамдық векторы бұрынғысынша хорданы бойлай бағытталады. Бірақ бұл сынық сызық біркелкі жатық қисыққа көбірек ұқсас екені көрініп түр.
Сондықтан түзу сызықты бөліктердің ұзындығын одан әрі кішірейте отырып (әрине, олардың санын көбейтіп), біз оларды нүктеге жақындатып жиырамыз, сонда сынық сызық біркелкі жатық қисыққа айналады. Бұл қисық сызықтың әрбір нүктесінде жыдамдық сол нүкте арқылы қисық сызыққа жүргізілген жанама бойымен бағытталады
Дененің қисық сызықты траекторияның кез келген нүктедегі лездік жылдамдығы траекторияның осы нүктесіне жүргізілген жанама бойымен бағытталады.
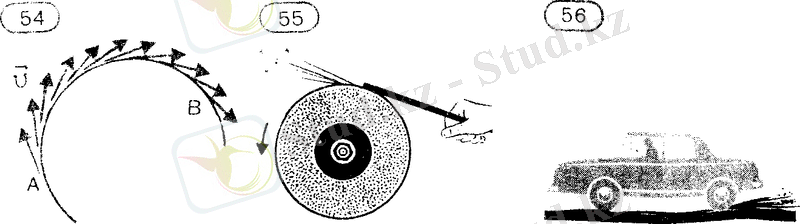
Қисық сызықты қозғалыста нүктенің жылдамдығы шынында да жанама бойымен бағытталғандығына, мысалы, қайрақтың жұмысын бақылап көз жеткізуге болады. Егер айналып тұрған қайрақ тасқа болат шыбықтың ұшын баса қойсақ, тастан шығып шашыраған қызған бөлшектер ұшқын тәрізденіп
көрінеді. Бөлшектер тастан бөлініп шықкан кезде қандай жылдамдық алса, сондай жылдамдықпен ұшады. Ұшқындардың шығу баратыны , болат шыбықтың тасқа тиіп тұрған нүктесінде, шеңберге жүргізілген жанамамен дәл келетіні суреттен айқын көрінеді. Сазға батқан автомобильдің доңғалағы астынан ұшатын саз балшық та шеңберге жанама бойымен ұшады.
Сөйтіп, дененің лездік жылдамдығы қисық сызықты траекторияның әрбір нүктелерінде, көрсетілгендей, түрлі бағыт алады. Жылдамдык модулі траекторияның барлық жерінде бірдей болуы немесе нүктеден нүктеге өзгеруі мүмкін.
Тіпті жылдамдық модулі өзгермесе де, бәрібір тұрақты деуге болмайды. Өйткені жылдамдық - векторлық шама. Ал векторлық шамалар үшін модуль мен бағыт екеуі де бірдей маңызды шамалар. Сондықтан жылдамдық модулі түрақты болған жағдайдың өзінде қисық сызықты қозгалыс әрқашан да үдемелі болады. Біз тек осындай қисық сызықты қозғалысты - жылдамдық модулі бойынша түрақты кисық сызықты қозғалысты қарасты-румен ғана шектелеміз. Оны бір қалыпты қисық сызықты қозғалыс деп атайды. Мұндай қозғалыста үдеу тек жылдамдықтың бағытының өзгеруімен ғана байланысты. Бүл үдеу қалай бағытталған және неге тең?
Қисық сызықты қозғалыс - шеңбер доғасы бойымен қозғалыс. Қисық сызықты қозғалыста жылдамдықтың бағыт бойынша өзгеруі, әрине, траекторияның пішініне байланысты болады. Ал қисық сызықтардың түрлері сансыз көп. Бірақ қозғалыстың әрбір жеке қисық сызықты траекторияларының бәрін бірдей қарастыра бермейміз.

Қайсыбір күрделі қисық сызықты траектория көрсетілген. Бұл суреттен, қисық сызықты траекторияның жеке бөліктері, шамамен шеңбер доғасы екені көрініп түр, олар пунктирмен кескінделген. Мысалы, КL бөлігі - бұл радиусы кішкене шеңбер доғасы, ЕҒ - бұл радиусы үлкен шеңбердің доғасы.
Сонымен, кез келген қисық сызықты траектория бойымен өтетін қозғалысты шамамен қайсыбір шеңбер доғалары бойымен болатын қозғалыс ретінде қарастыруға болады. Сондықтан қисық сызықты бір қалыпты қозғалыстарда үдеуді табу мәселесі дененің шеңбер бойымен бір қалыпты қозғалғандағы үдеуін іздестіруге тіреледі.
ШЕҢБЕР БОЙЫМЕН БІР ҚАЛЫПТЫ ҚОЗҒАЛҒАН ДЕНЕНІҢ ҮДЕУІ
Шеңбер бойымен бір қалыпты қозғалған дененің қозғалысы, жылдамдық модулі өзгермесе де - бұл үдемелі қозғалыс. Енді біздің мақсатымыз осы үдеудің қалай бағытталатынын және оның неге тең болатынын айқындау.
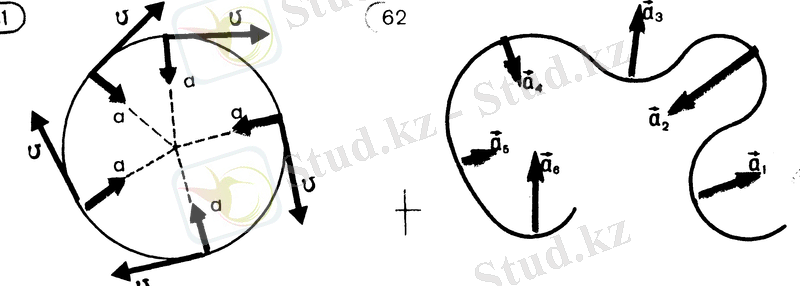 Үдеу векторы центрге бағытталған.
Үдеудің
Үдеу векторы центрге бағытталған.
Үдеудің
теңдігімен анықталатыны белгілі. Ықшамдау үшін жылдамдықтың екі мәнінің айырмасын, яғни оның
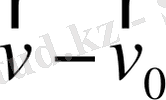 өзгеруін
өзгеруін
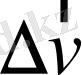 арқылы белгілейік. Сонда
арқылы белгілейік. Сонда
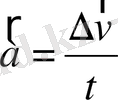
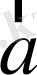 векторы
векторы
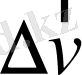 векторы сияқты бағытталатыны айқын, өйткені уақыт t - скаляр шама.
векторы сияқты бағытталатыны айқын, өйткені уақыт t - скаляр шама.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz