Комплекс сандарға кіріспе: анықтау, операциялар және тригонометриялық форма


Алгебраның бастамасы теріс сандарды енгізумен, яғни бүтін сандар жүйесін қарастырудан және оны одан әрі барлық бөлшек сандар мен бүтін сандар жиынтығынан тұратын райионал сандар жүйесіне кеңейтуден басталады.
Рационал сандар жүйесін кеңейту иррационал сандарды енгізумен байланысты. Барлық рационал және барлық иррационал сандар жиынтығынан тұратын жүйе нақты сандар деп аталады.
Элементарлық алгебра курсының соңына қарай нақты сандар жүйесі қарастырылады. Комплекс сандардың енгізілу себебі, кейбір нақты коэффициентті квадрат теңдеулерді нақты сандар жиынында шешуге мүмкін еместігінен туындаған. Мысалы,
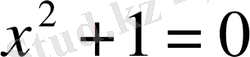 (1)
(1)
Сонымен, нақты сандар жүйесін (1) теңдеудің түбірлері болатындай сандар жүйесіне дейін кеңейтуіміз керек.
Жаңа сандар жүйесін кеңейту үшін керекті материалдар ретінде, біз жазықтықтағы нүктелерді аламыз. Нақты сандарды түзу бойын толтырып бейнелеуге болатын. Енді біз жазықтықтың барлық нүктелерін бейнелей алатын сандар жүйесін анықтағымыз келеді.
Жазықтықта тік бұрышты координаталар жүйесі анықталған болсын. Жазықтық нүктелерін
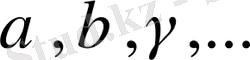 әріптерімен белгілеп және абциссасы a, ординатасы
b
болатын
a
нүктені
a=(a, b)
деп белгілеуге келіселік. Егер
әріптерімен белгілеп және абциссасы a, ординатасы
b
болатын
a
нүктені
a=(a, b)
деп белгілеуге келіселік. Егер
a=(a, b)
және
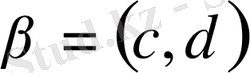 екі нүкте берілсе, онда олардың
қосындысы
деп абциссасы
а+с
және ординатасы
b+d
болатын нүктені алалық, яғни
екі нүкте берілсе, онда олардың
қосындысы
деп абциссасы
а+с
және ординатасы
b+d
болатын нүктені алалық, яғни
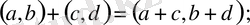 (2)
(2)
ал көбейтіндісі деп абциссасы a*c-b*d және ординатасы a*d+b*c , яғни
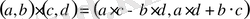 (3)
(3)
нүктесін алалық.
Осы жолмен жазықтықтың барлық нүктелері үшін екі алгебралық операция анықтадық. Бұл операциялар нақты сандар жүйесіндегі немесе рационалл жүйесіндегі тәріздес коммутативтік және олар үшін кері операциялар - алу және бөлу (нольге бөлуден өзге) анықталған.
Сонымен, біз жазықтықтың нүктелеріне бейнеленетін бұл сандар үшін операциялар (2), (3) формулаларымен анықталатын сандар жүйесін құрдық. Бұл сандар жүйесі комплекс сандар жүйесі деп аталады.
Енді квадраты-1-ге тең, теңдеудің (1) түбірі бола алатын комплекс санды ізделік. Мысалы, ордината осінде жататын (0, 1) санының квадратын (3) формуламен есептесек, онда:
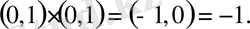
Бұл нүктені
i
деп белгілелік яғни
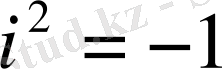
Енді
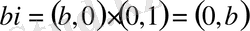 және
және
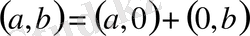 және
және
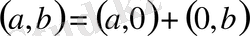 екенін ескерсек, онда
екенін ескерсек, онда
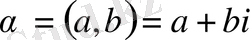
 комплекс саны үшін
а
саны нақты бөлігі, ал
bi
-жорымал бөлігі делінеді.
комплекс саны үшін
а
саны нақты бөлігі, ал
bi
-жорымал бөлігі делінеді.
a+bi және a-bi комплекс сандары түйіндес деп аталады.
Комплекс сандарға амалдар қолдану
- Қосу, көбейту, алу және бөлу. a+biтүрінде жазылған комплекс сандарды қосу, көбейту, алу және бөлу төмендегіше орындалады:
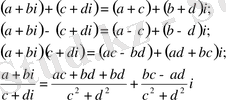
Мысалдар.
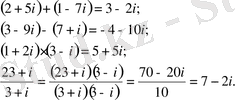
- Комплекс санды тригонометриялық түрде жазу.
- Нүктенің жазықтықта орналасуын пляр координаталары арқылы да анықтауға болатыны белгілі. Бұл жағдайдаrсаны а комплекс саныныңмодулідеп аталып, деп белгіленеді, албұрышыаргументідеп аталып, деп белгіленеді.
және
. Сонда кез келген a=a+bi комплекс саны үшін
немесе
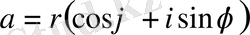
Бұл жазылу комплекс санның тригонометриялық түрде жазылуы деп аталады.
Тригонометриялық түрде жазылған екі комплекс санды көбейтіп көрелік:
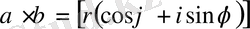
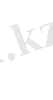
Тригонометриялық түрде жазылған екі комплекс санды көбейтіп көрелік:
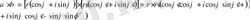
немесе
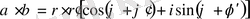 (5)
(5)
Яғни көбейтіндінің модулі модулдердің көбейтіндісіне , ал көбейтінідінің аргументі аргументтердің қосындысына тең . Бөлгенде керісінше болатынын көреміз.
Комплекс саннан түбір табу
1.
Муавр формуласы
.
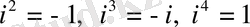 және (5) ережені ескеріп,
а
санын оң бүтін
n
дәрежеге шығарсақ
Муавр формуласын
және (5) ережені ескеріп,
а
санын оң бүтін
n
дәрежеге шығарсақ
Муавр формуласын
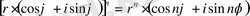 (6)
(6)
аламыз. Мысалы,
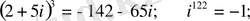
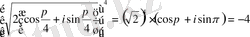
Муавр формуласынан
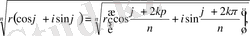 (7)
(7)
мұндағы, k=0, 1, 2, …n-1.
Мысалы:
1)
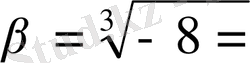
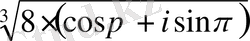
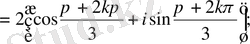
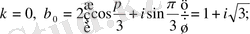
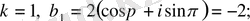
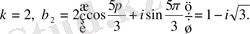
2)
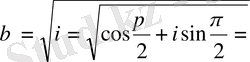
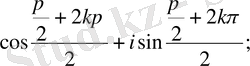
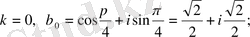
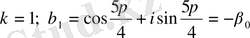
2 . Бірдің түбірлері . 1 санынан n-ші дәрежелі түбір таба білу маңызды деп есептеледі. 1=cos0+isin0 теңдігін (7) формуланың көмегімен 1-дің n -ші дәрежелі түбірдің мына формуламен
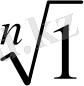
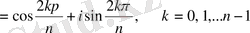 (8)
(8)
табамыз.
Егер а санының n-ші дәрежелі бір түбірін білсек, онда қалған түбірлерін осы түбірді 1 санының дәрежелі түбірлеріне көбейту арқылы тауып алуға болады.
Мысалы, 1 санының кубтық түбірлері мынадай:
1,
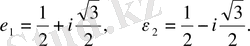
Ал -8 санының кубтық түбірлерінің бірі -2.
Комплекс сандарды геометриялық кескіндеу
Тік төртбұрышты координат жүйесіндегі жазықтықты қарастыралық. Әрбір z=x+iy комплекс санына жазықтықтың координаттары х пен у болатын бір ғана нүктесі сай келеді. Сөйтіп, жазықтықтың нүктелерін комплекс сандар деп айтуға болады. Бұл жағдайда жазықтықтың өзін комплекс жазықтық деп айтуға болады, ал z -ті осы жазықтықтың нүктесі дейді.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz