Кездейсоқ шама үлестіру функциясы: дискретті, үздіксіз және аралас түрлері мен қасиеттері


Кездейсоқ шамаларды қарастырғанда, дискретті және үздіксіз шамалардың болатынын айттық. Сондықтан дискретті кездейсоқ шамалардың үлестіруімен қатар үздіксіз кездйесоқ шамалардың да үлестіруін қарастырамыз.
Кездейсоқ шаманың үлестіру функциялары. Кездейсоқ шама үздіксіз болғанда,
 мәніндегі оқиғалар ұғымын пайдаланбайды, мұның орнына
мәніндегі оқиғалар ұғымын пайдаланбайды, мұның орнына
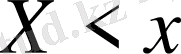 теңсіздігін алады. Мұндағы х - айнымалы шама. Бұл теңсіздікті, кездейсоқ шама Х - тен кіші болатын барлық мүмкін мәндерді қабылдайды деп айтылады, яғни
теңсіздігін алады. Мұндағы х - айнымалы шама. Бұл теңсіздікті, кездейсоқ шама Х - тен кіші болатын барлық мүмкін мәндерді қабылдайды деп айтылады, яғни
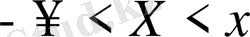 . Сөйтіп, оның ықтималдығын
. Сөйтіп, оның ықтималдығын
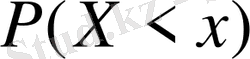 түрінде жазады.
түрінде жазады.
Бұдан кездейсоқ шама Х-тің қабылдайтын мәндерінің ықтималдығы х айнымалысы мәніне байланысты екенін көреміз. Сондықтан бұл ықтималдық Х-тің кейбір функциясы болады, оны
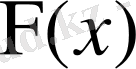 деп белгілесек, онда
деп белгілесек, онда
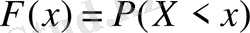 немесе
немесе
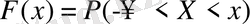 (1) болады. Бұл функцияның үлестіру функциясы немесе үлестірудің интегралдық функциясы, немесе кездейсоқ шама үлестіруінің интегралдық заңы, немесе кездейсоқ шамаықтималдықтарының үлестіру функциясы деп атайды. Бұл функция әрі, дискретті, әрі үздіксіз кездейсоқ шамаларды сипаттайды.
(1) болады. Бұл функцияның үлестіру функциясы немесе үлестірудің интегралдық функциясы, немесе кездейсоқ шама үлестіруінің интегралдық заңы, немесе кездейсоқ шамаықтималдықтарының үлестіру функциясы деп атайды. Бұл функция әрі, дискретті, әрі үздіксіз кездейсоқ шамаларды сипаттайды.
Х дискретті кездейсоқ шама болса, онда ол шекті немесе саналымды шексіз мәнді қабылдайды және оның әрбір
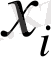 мәніндегі ықтималдық
мәніндегі ықтималдық
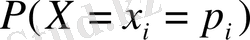 болады. Сондықтан
болады. Сондықтан
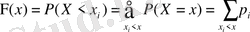
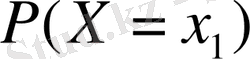 символы
символы
 теңсіздігінің барлық мүмкін мәндері үшін алынды деп ұғылады. (1) өрнегі
теңсіздігінің барлық мүмкін мәндері үшін алынды деп ұғылады. (1) өрнегі
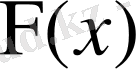 туралы барлық информацияны толық береді. Бұл функция графигі суретте Х-тің қабылдаған дербес х
1
, х
2
. . . х
n
мәндері үшін келтірілді.
туралы барлық информацияны толық береді. Бұл функция графигі суретте Х-тің қабылдаған дербес х
1
, х
2
. . . х
n
мәндері үшін келтірілді.
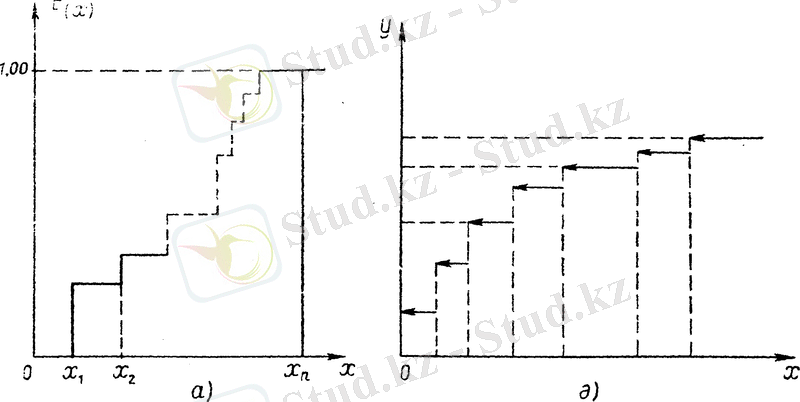
Графикте бұларға сәйкес
 ықтималдықтары вертикаль кесінділер қосындысына тең. Бұл кесінділер (х, 0) нүктесінен өтетін ордината осіне параллель түзуден сол жаққа орналасқанын байқауға болады.
ықтималдықтары вертикаль кесінділер қосындысына тең. Бұл кесінділер (х, 0) нүктесінен өтетін ордината осіне параллель түзуден сол жаққа орналасқанын байқауға болады.
Графикті біртұтас қарастырса, онда үлестіру функциясы баспалдақты, үзілісті болып кездейсоқ шаманың (Х-тің) іргелес жатқан
 және
және
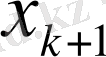 мәндерінен жасалған әрбір аралықта тұрақты болуын байқаймыз. Мұның секірмелі нүктелері - х
1
, х
2
. . . х
n
. Секірме шамасы сәйкес
мәндерінен жасалған әрбір аралықта тұрақты болуын байқаймыз. Мұның секірмелі нүктелері - х
1
, х
2
. . . х
n
. Секірме шамасы сәйкес
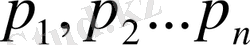 ықтималдықтарына тең. Сонымен, бұл нүктелерде
ықтималдықтарына тең. Сонымен, бұл нүктелерде
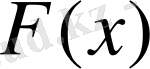 мәні нөлге тең болады. х
n
нүктесінен оңға қарай
мәні нөлге тең болады. х
n
нүктесінен оңға қарай
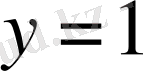 түзуімен дәл келеді, сөйтіп
түзуімен дәл келеді, сөйтіп
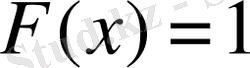 болады. Мұнда
болады. Мұнда
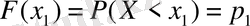
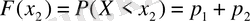

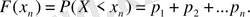
Былайша айтқанда, бұл функцияны кумулятивтік функция деп те атайды, яғни бұл - өзіне дейінгі мәндердің өз мәнімен қосылуынан құрылған функция.
1 - мысал. Лоторея ұтысынң үлестіру таблицасы бойынша үлестіру функциясын анықтап және графигін сызу керек.
 Шешуі:
Шешуі:
 болсын, ал есептің шарты бойынша Х теріс таңбалы мәнді қабылдамайды, сондықтан Х-тің мәні
болсын, ал есептің шарты бойынша Х теріс таңбалы мәнді қабылдамайды, сондықтан Х-тің мәні
 - ден кіші болуы мүмкін емес, олай болса,
- ден кіші болуы мүмкін емес, олай болса,
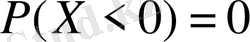 , өйткені мүмкін емес оқиға ықтималдығы нөлге тең. Демек,
, өйткені мүмкін емес оқиға ықтималдығы нөлге тең. Демек,
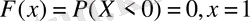 , болса, онда
, болса, онда
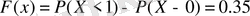 , яғни
, яғни
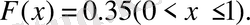 Сондай - ақ
Сондай - ақ
 болғанда
болғанда
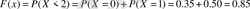 , яғни
, яғни
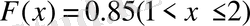 .
.
 болғанда
болғанда
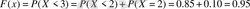 , яғни
, яғни
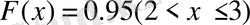 .
.
 болғанда
болғанда
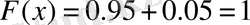 , яғни
, яғни
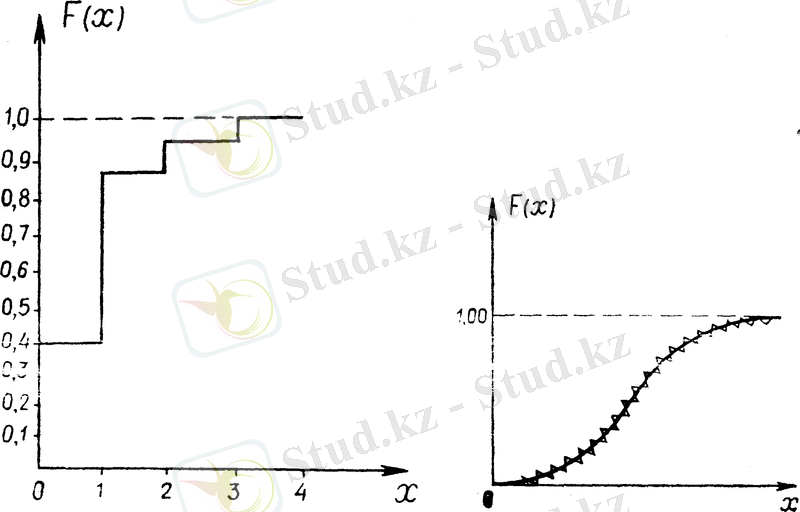
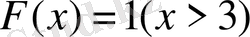 . Мұның графигі:
. Мұның графигі:
Бұл үлестіру функциясының графигі баспалдақты сынық сызық. Дискретті кездейсоқ шаманың әрбір мәні
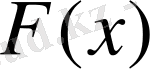 секірімі Х-тің ықтималдығына тең. Осы мысалдан дискретті кездейсоқ шаманың үлестіру функциясы бойынша оның үлестіру заңын қалпына келтірудің қиын еместігін байқаймыз.
секірімі Х-тің ықтималдығына тең. Осы мысалдан дискретті кездейсоқ шаманың үлестіру функциясы бойынша оның үлестіру заңын қалпына келтірудің қиын еместігін байқаймыз.
Жалпы
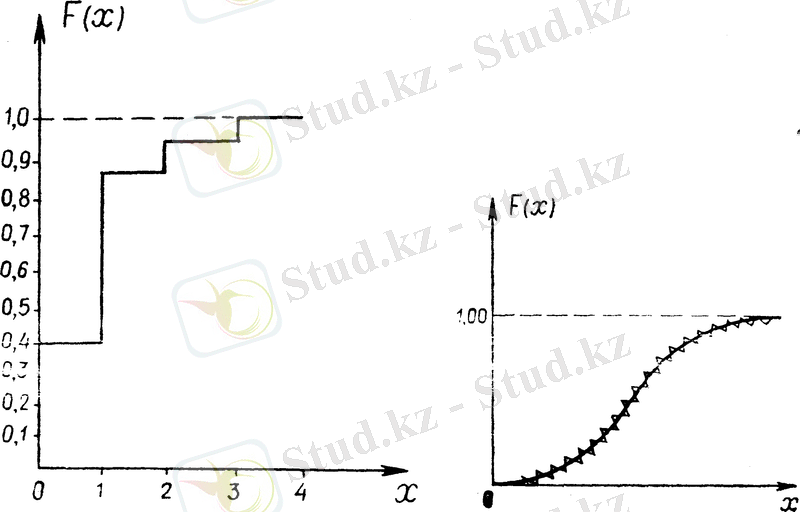
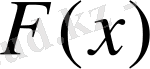 функциясының барлық секірмелері қосындысы 1-ге тең. Ал кездейсоқ шаманың қабылдайтын мүмкін мәндерін арттыра берсек, олардың арасындагы интервалы кеми береді де, секірме саны арта түседі, бірақ ол секірмелер шамасы азая түседі. Сөйтіп, баспалдақты қисық жатық бола отырып кездейсоқ шама үздіксіз кездейсоқ шамара бірте-бірте жақындай түседі де,
кумулятивтік функция
үздіксіз үлестіру функциясына жуықтайды. Жалпы үздіксіз кездейсоқ шаманың үлестіру функциясы болып нүктеде үздіксіз болады.
функциясының барлық секірмелері қосындысы 1-ге тең. Ал кездейсоқ шаманың қабылдайтын мүмкін мәндерін арттыра берсек, олардың арасындагы интервалы кеми береді де, секірме саны арта түседі, бірақ ол секірмелер шамасы азая түседі. Сөйтіп, баспалдақты қисық жатық бола отырып кездейсоқ шама үздіксіз кездейсоқ шамара бірте-бірте жақындай түседі де,
кумулятивтік функция
үздіксіз үлестіру функциясына жуықтайды. Жалпы үздіксіз кездейсоқ шаманың үлестіру функциясы болып нүктеде үздіксіз болады.
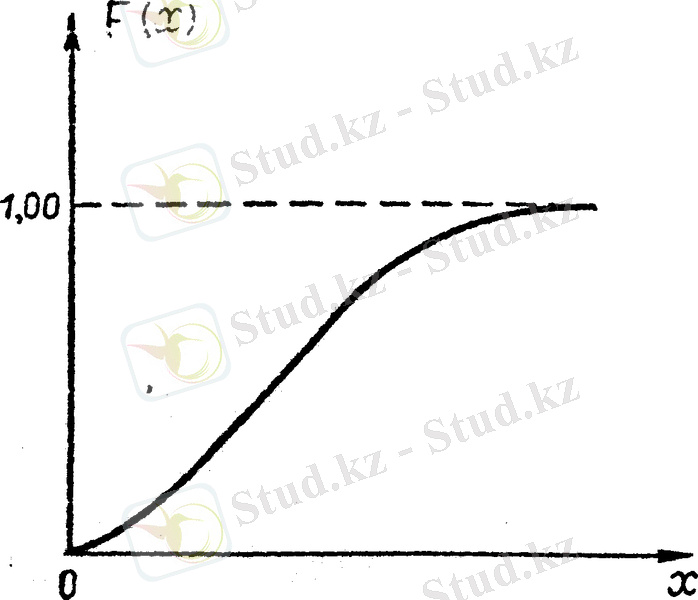
Ал бұл екі кездейсоқ шамадан басқа үшінші түрдегі шама аралас кездейсоқ шама деп аталады. Бұл жағдайда кездейсоқ шаманың мүмкін мәндері кейбір аралық үздіксіз, оны біртұтас толтырады, бірақ үлестіру функциясы оның барлық нүктесінде үздіксіз емес, яғни кейбір нүктеде үзіледі. Сонымен, аралас кездейсоқ шаманың үлестіру функциясы секірме саны саналымды саннан артық емес, бөлікті-үздіксіз функция екен көреміз. Мұның үлестіру функциясын
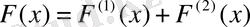 түрінде жазуға болады.
түрінде жазуға болады.
Мұндағы
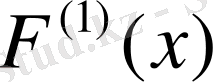 үздіксіз дифференциялданатын функция,
үздіксіз дифференциялданатын функция,
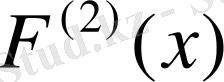 нүктесінен солға қарай жатқан секірмелер қосындысы.
нүктесінен солға қарай жатқан секірмелер қосындысы.
Сөйтіп, аралас кездейсоқ шаманың үлестіру фунциясы дискретті және үздіксіз кездейсоқ шамалар түрлерін біріктіріп отыр, яғни бұл жағдайда
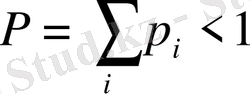
қатар үлестірумен
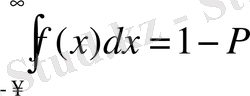
Болатын теріс емес, интегралданатын функция
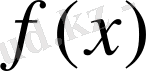 - ті қамтиды. Сонда
- ті қамтиды. Сонда
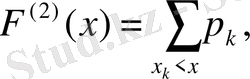
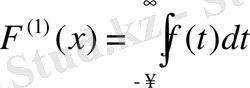
болады. Соңғы қосынды
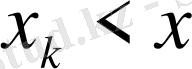 теңсіздігі орындалатын
теңсіздігі орындалатын
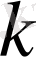 - ның барлық мәнінде алынғанын білдіреді. Бұдан
- ның барлық мәнінде алынғанын білдіреді. Бұдан
 шек алынса, онда
шек алынса, онда
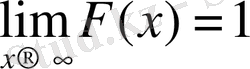 болады. Өйткені
болады. Өйткені
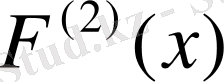 қосындысы Р-ға, ал
қосындысы Р-ға, ал
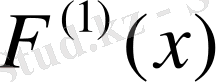 интегралы 1-Р - ға тең.
интегралы 1-Р - ға тең.
Дискретті, үздіксіз және аралас кездейсоқ шамалардың үлестіру функцияларының жазылуы бірізді болу үшін және үлестіру функцияларына қолданатын операцияларды формальдау үшін
 , болғанда, 1-ге тең,
, болғанда, 1-ге тең,
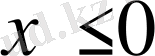 болғанда, 0-ге тең болатын бірлік функция
болғанда, 0-ге тең болатын бірлік функция
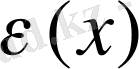 -ті енгізеді. Сонда дискретті кездейсоқ шама үшін
-ті енгізеді. Сонда дискретті кездейсоқ шама үшін
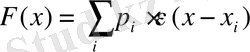
аралас кездейсоқ шама үшін
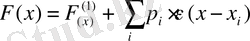
болады. Ал дельта функциясын пайдаланып ықтималдық тығыздығын да бірізді жазуға болады.
Үлестіру функциясының қасиеттері:
Дискретті және үздіксіз кездейсоқ шамаларды сипаттайтын үлестіру функцияларының қасиеттерін келтірейік.
1° - қасиет.
х-тің әрбір мәнінде
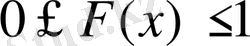 болады.
болады.
Дәлелдеуі:
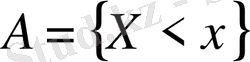 дейік. Ал
дейік. Ал
 болғандықтан,
болғандықтан,
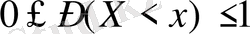 болады.
болады.
2° - қасиет.
Кездейсоқ шама Х-тің үлестіру функциясын аргументінің теріс теріс емес, кемімейтін функциясы болады, яғни
 болғанда,
болғанда,
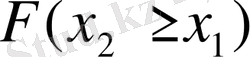 .
.
Дәлелдеуі:
 болса,
болса,
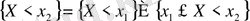 . Мұнда
. Мұнда
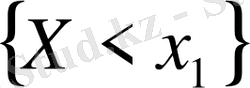 және
және
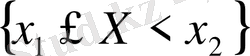 оқиғалары үйлесімсіз. Олай болса,
оқиғалары үйлесімсіз. Олай болса,
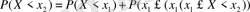 .
.
Бұдан
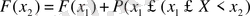
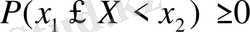 ,
,
Демек,
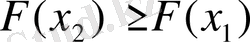 ,
,
3° - қасиет
.
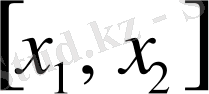 аралығындағы мәндерді қабылдайтын кездейсоқ шама Х-тің ықтималдығы осы интервалдығы
аралығындағы мәндерді қабылдайтын кездейсоқ шама Х-тің ықтималдығы осы интервалдығы
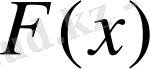 функциясының өсімшесіне тең, яғни
функциясының өсімшесіне тең, яғни
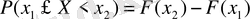
4° - қасиет
.
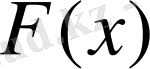 функциясы
функциясы
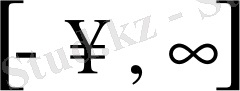 аралығының кез келген
аралығының кез келген
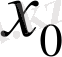 нүктесінде сол жағынан үздіксіз, яғни
нүктесінде сол жағынан үздіксіз, яғни
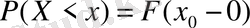
5° - қасиет
. Егер
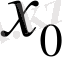 нүктесінде жинақталатын өспелі емес
нүктесінде жинақталатын өспелі емес
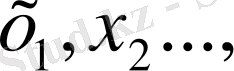 тізбегі берілсе, онда
тізбегі берілсе, онда

6° -қасиет.
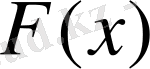 функциясының секірмелі саналымды жиыннан артық болмайды.
функциясының секірмелі саналымды жиыннан артық болмайды.
7° -қасиет.
Егер Х кездейсоқ шамасы
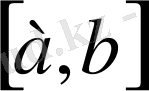 аралығындағы барлық мәндерді қабылдаса, онда х-тің а-дан кіші барлық мәндерінде
аралығындағы барлық мәндерді қабылдаса, онда х-тің а-дан кіші барлық мәндерінде
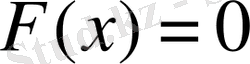 , ал
, ал
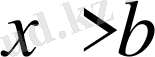 мәндерінде
мәндерінде
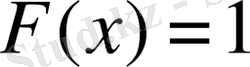 .
.
8° -қасиет.
Егер кездейсоқ шама
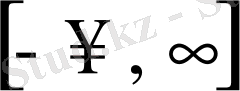 аралығындағы кез келген мәнді қабылдаса, онда мына теңдіктер орындалады.
аралығындағы кез келген мәнді қабылдаса, онда мына теңдіктер орындалады.
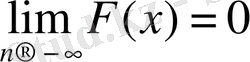
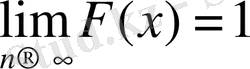
9° -қасиет.
Үздіксіз шаманың әрбір жеке мәніндегі ықтималдығы 0-ге тең. Яғни
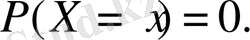 Бұны былай деп атауға болады.
Бұны былай деп атауға болады.
 нүктесі
нүктесі
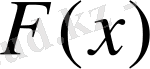 -тің үздіксіздік нүктесі болса, онда
-тің үздіксіздік нүктесі болса, онда
 оқиғасының ықтималдығы
оқиғасының ықтималдығы
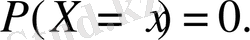 тең.
тең.
Осы келтірілген 9 қасиет негізінде үздіксіз кездейсоқ шамаға мынадай анықтама беруімізге мүмкіндік туады. Егер х-тің әрбір мәнінде
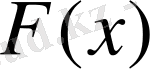 үлестіру функциясын үздіксіз деп айтады.
үлестіру функциясын үздіксіз деп айтады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz