Кванттық механика негіздері: шексіз потенциалдық шұңқыр, туннель эффектісі, операторлар, де-Бройль толқындары және спин


Тақырыбы: Шексіз терең потенциалдық шұңқырдағы бөлшек туралы есеп .
Лекция жоспары:
- Шексіз терең потенциалдық шұңқырдағы бөлшек туралы есеп.
- Бөлшектердің потенциалдық тосқауылдан өтіп кетуі.
1. Айталық элементер бөлшек бір өлшемді шексіз терең шұңқырдың ішінде қозғалыста болсын. Бөлшектің қозғалысы x осінің бойымен бағытталсын (1 -сурет) . Сонда бөлшектің қозға-
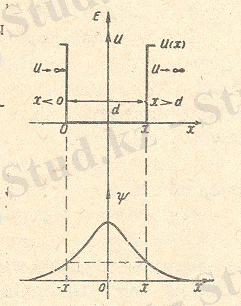 лысы қабырғалары
x=0
және
x=d
шектелген тік бұрышты потенциалдық шұңқырдың ішінде болуына сәйкес оның потенциалдық энергиясы шұңқырдың ішінде 0-ге тең
U=0
ал, координаталары
x<0
және
x>d
болатын сыртқы жақтарындағы потенциалық энергияның мәндері шексіздікте өседі,
лысы қабырғалары
x=0
және
x=d
шектелген тік бұрышты потенциалдық шұңқырдың ішінде болуына сәйкес оның потенциалдық энергиясы шұңқырдың ішінде 0-ге тең
U=0
ал, координаталары
x<0
және
x>d
болатын сыртқы жақтарындағы потенциалық энергияның мәндері шексіздікте өседі,
 .
.
Сөйтіп, бөлшек қабырғалары шексіз потенциалдық шұңқырдың
сыртындағы энергияның мәні ішіндегі энергиядан әлдеқайда
көбірек болады.
Бөлшек х осінің бағытымен қозғалыста болғандықтан, ψ
функциясы осы бір координатқа тәуелділігі бойынша сәйкес
Шредингер теңдеуін осы бөлшек қозғалысы үшін мынаны
жазуға болады.
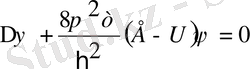 (1)
(1)
мұндағы
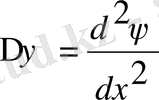
Егер бөлшек потенциалдық шұңқыр ішінде десек, яғни
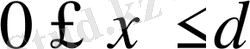 болса, онда (1) -ші теңдеу мына түрде жазылады (U=0)
болса, онда (1) -ші теңдеу мына түрде жазылады (U=0)
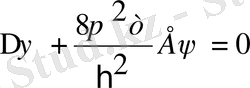 (2)
(2)
- теңдеудің жалпы шешуі болып мына өрнек есептеледі
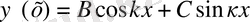 (3)
(3)
мұндағы В және С - тұрақты шамалар.
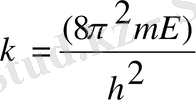 (4)
(4)
Бұдан бөлшектің кинетикалық энергиясы
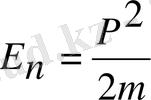 оның потенциалдық шұңқырдан шы-ғып кетуіне жеткіліксіз болса, онда
x=0
және
x=d
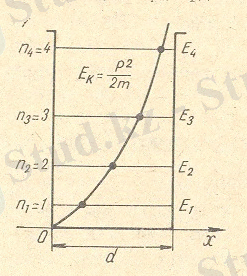
болғанда ғана толқындық функцияның мәні нөлге айналады (2-ші сурет) . Олай болса,
x=0
болғанда
оның потенциалдық шұңқырдан шы-ғып кетуіне жеткіліксіз болса, онда
x=0
және
x=d
болғанда ғана толқындық функцияның мәні нөлге айналады (2-ші сурет) . Олай болса,
x=0
болғанда
 болып (3) -ші теңдеудің оң жағын-дағы екі мүшесі де нолге айналады. Сонда В+С = 0 болар еді де, В = - С. Сөйтіп функцияның мә-ні мынадай түрге келеді:
болып (3) -ші теңдеудің оң жағын-дағы екі мүшесі де нолге айналады. Сонда В+С = 0 болар еді де, В = - С. Сөйтіп функцияның мә-ні мынадай түрге келеді:
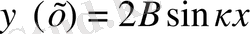 . Ал
x=d
болса, онда
. Ал
x=d
болса, онда
 де,
де,
 (
п=1, 2, 3 . . .
)
(
п=1, 2, 3 . . .
)
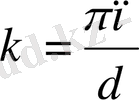 енді осы
енді осы
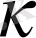 - ның
- ның
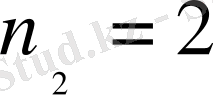 мәнін қойып, мына өрнекті аламыз.
мәнін қойып, мына өрнекті аламыз.
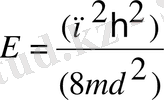 (5)
(5)
Сөйтіп потенциалдық шұңқыр ішіндегі бөлшектің толық энер-гиясының мәні болмай, тек п 2 саны сәйкес белгілі бір мәндері ғана бола алады (5) формуладағы п бөлшектің энергиясы квантталғандығын көр-сетеді. Егер п шамасы-ның белгілі бір сан мәндерін қою арқылы потен-циалдық шұңқыр ішіндегі бөлшектің энергетикалық деңгейлерін
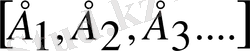 анықтауға болады. (2-ші сурет) мұндағы
п
- бөлшектің энергетикалық деңгейле-рін сипаттайтын кванттық сандарда бөлшектің қандай кванттық күйде екендігін көрсетеді. Олай болса, кванттық санның мәніне сәйкес оның кинетикалық энергиясының (Е
к
) мәндері де өзгеріп отырады.
анықтауға болады. (2-ші сурет) мұндағы
п
- бөлшектің энергетикалық деңгейле-рін сипаттайтын кванттық сандарда бөлшектің қандай кванттық күйде екендігін көрсетеді. Олай болса, кванттық санның мәніне сәйкес оның кинетикалық энергиясының (Е
к
) мәндері де өзгеріп отырады.
2.
Кванттық механика бөлшектің классикалық механикадағы макро бөлшектің принциптік айырмашылығы ерекше көрінетін құрылыс олардың жолындағы потенциалдық тосқауылдан ол кездескен кездегі «тәртібі» L классикалық бөлшекті қарастырсақ оның жалпы энергиясы Е тосқ-ауылдың биіктігі U<0 болса, бөлшек 1-ші аймақтан 2-і аймаққа өтіп кете алмайды. Ал электрон E<U
0
қарастырсақ оған тән де Бройль толқыны болады. Толқынның таралуына ешқандай кедергі болмайды, ол тосқауылдың шекарасында толық шағылады да, толқынның бір бөлігі 1-ші аймақ-тан 2-ші аймаққа өтіп кетуі мүмкін. Басқаша айтқанда, электрондардың тосқауылдың 2-ші жағын-да кездестірудің белгілі бір мүмкіндігі бар. Міне бұл классикалық механика мен кванттық меха-никаның тұжырымдарының негізгі айырмашылықтарының бірі. Әрбір көрсетілетін аймақ үшін
Шредингер теңдеуін
жазамыз
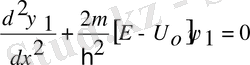 мұндағы U
0
=0 болғандықтан 1-ші аймақ-тағы бөлшектің теңдеуінің формуласы былай жазылады:
мұндағы U
0
=0 болғандықтан 1-ші аймақ-тағы бөлшектің теңдеуінің формуласы былай жазылады:
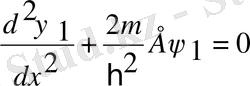 (1)
(1)
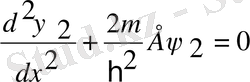 (2)
(2)
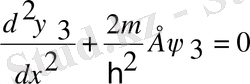 (3)
(3)
1-ші және 3-ші аймақ
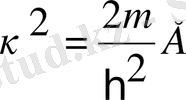 ,
2-ші аймақ
,
2-ші аймақ
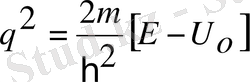
болады деп алып, осы 3 аймақ үшін Шредингер теңдеуінің шешімін былайша жазамыз:
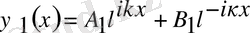 (4)
(4)
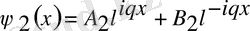 (5)
(5)
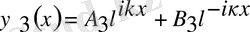 (6)
(6)
мұндағы А 1 - сол жақтан тосқауылға түскен толқынның амплитудасы.
В 1 - тосқауылдан шығатын 1-ші аймақтағы толқынның амплитудасы.
А 2 - тосқауыл арқылы 2-ші аймаққа өткен толқынның амплитудасы.
В 2 - тосқауыл ішінде, 2-ші аймақтағы шығылған толқынның амплитудасы.
А 3 - 3-ші аймаққа өткен толқынның амплитудасы.
В 3 - аймақта шағылған толқынның амплитудасы.
Графикте көрсеткендей 2-ші аймақтағы толқын
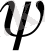 функциясы нольге тең емес, ал 3-ші ай-мақтағы де Бройль толқындарының жиіліктері 1-ші аймақтағы толқынның жиілігімен бірдей, тек амплитудасы кіші. Міне сонымен кванттық механика заңдары жаңа кванттық құбылысқа әкелді. Бұл құбылысты
туннельдік эффект
деп атайды. Туннельдік эффекті сипаттау үшін тосқауылдың мөлдірлігі деген шама енгізілген:
функциясы нольге тең емес, ал 3-ші ай-мақтағы де Бройль толқындарының жиіліктері 1-ші аймақтағы толқынның жиілігімен бірдей, тек амплитудасы кіші. Міне сонымен кванттық механика заңдары жаңа кванттық құбылысқа әкелді. Бұл құбылысты
туннельдік эффект
деп атайды. Туннельдік эффекті сипаттау үшін тосқауылдың мөлдірлігі деген шама енгізілген:
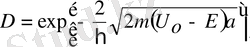 (7)
(7)
Тақырыбы: Физикалық шамалардың операторлары .
Лекция жоспары:
- Оператор туралы түсінік. Физикалық шамалардың операторлары.
- Энергияның операторы. Кинетикалық және потенциалдық энергиялардың операторлары.
- Гамильтон операторы.
- Оператор түріндегі Шредингер теңдеуі.
1.
Біз осыған дейін Шредингер теңдеуін біліп келдік. Шредингер теңдеуімен энергияның мүмкін мәндерін анықтауға және бөлшектің толқындық функциясын анықтауға болады. Меха-никада энергияны табумен шектелуге болмайды. Импульс координаттарын және импульс мо-ментін табу керек. Бұл шамаларды Шредингер теңдеуінен таба алдмаймыз. Сондықтан физика-лық шамаларды анықтайтын басқа теңдеу табу керек. Егер кванттық механикаға оператор қол-данатын математикалық аппаратты енгізсе басқа физикалық шамалар үшін теңдеуді қалай құру керек екендігі түсінікті болар еді. Оператор деп - бір функцияның көмегімен екінші функцияны алатын математикалық амалды акйтады.
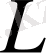 - оператордың белгіленуі. Кванттық механикада сызықтық оператор ғана қолданылады. Екі функцияның қосындысына әсері сол функциялардың әрқайсысына әсердің қосындысы арқылы анықталатын операторды
сызықтық
деп атайды.
- оператордың белгіленуі. Кванттық механикада сызықтық оператор ғана қолданылады. Екі функцияның қосындысына әсері сол функциялардың әрқайсысына әсердің қосындысы арқылы анықталатын операторды
сызықтық
деп атайды.
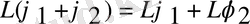 ;
;
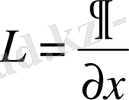 болсын,
болсын,
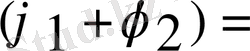
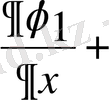
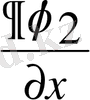 сызықтық операторлар. Көбейту операторлары:
сызықтық операторлар. Көбейту операторлары:
 ;
;
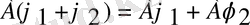 бұл да сызықтық, интеграл операторла-ры да, сызықтық логарифм мен дәреже көрсеткіш операторлары сызықтық емес.
бұл да сызықтық, интеграл операторла-ры да, сызықтық логарифм мен дәреже көрсеткіш операторлары сызықтық емес.
Екі оператор
коммутативті
деп аталады. Егер оларды кез келген функцияға қолдану нәти-жесі олардың қолдану ретіне тәуелді болмаса. Екі операторды қарастырамыз оларды φ функциясына қолданамыз.
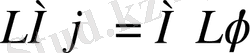 ;
;
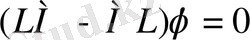 . Егер екі нәтижеде тең болса, онда олар коммутативті φ - кез келген функция, сондықтан жақша нольге тең.
. Егер екі нәтижеде тең болса, онда олар коммутативті φ - кез келген функция, сондықтан жақша нольге тең.
 - коммутативтік шарты.
- коммутативтік шарты.
Кванттық механикада операторлық түрге ауысқан кезде мына түрде жүреді.
- Классикалық механиканың әрбір физикалық шамасына кванттық механикада операторларды сәйкестендіріп алады. Бұл оператор оператордың өздік мәні берілген физикалық шамасын мүмкін мәні болатындай етіп таңдап алынады. Физикалық шаманың мәні айқын болғандықтан міндетті түрде өздік мәні айқын өз-өзіне түйіндес операторды қабылдау керек.
- Операторларды классикалық механикада физикалық шамалардың арасындағы қатынас та сондай болатындай етіп таңдап алу керек. Физикалық шаманың операторлары классикалық механиканың сол әріптерімен белгіленеді.
Мысалы:
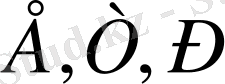 т. б. Классикалық механикада барлық физикалық шамалар координаттың және импульстің функциясы түрінде беріледі. Мысалы: Е (x, y, z, P), U(x, y, τ),
т. б. Классикалық механикада барлық физикалық шамалар координаттың және импульстің функциясы түрінде беріледі. Мысалы: Е (x, y, z, P), U(x, y, τ),
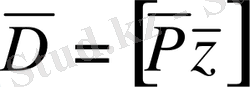 импульс моменті.
импульс моменті.
Егер импульстің проекциясы үшін және координата үшін операторды да тапсақ, онда қалған операторды сәйкестілік принципі бойынша табуға болады.
2
.
де Бройль толқыны берілген энергияның күйін сипаттайды, яғни де бройль толқыны энергия үшін оператордың өздік функциясы болады:
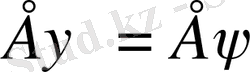 қандай амал қолдану керек? Уақыт бойынша дифференциалдаймыз. Сонда
энергияның операторы
қандай амал қолдану керек? Уақыт бойынша дифференциалдаймыз. Сонда
энергияның операторы
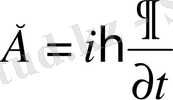 .
.
Кинетикалық энергияның операторы . Кинетикалық энергияның классикалық функциясы мына түрде болатын:
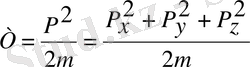
Сәйкестілік принципі бойынша операторлар арасындағы қатынас физикалық шамалар арасындағы қатынастай болады:
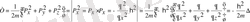 .
.
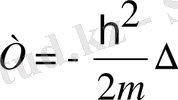
Потенциалдық энергия операторы
Потенциалдық энергия үшін жалпы теңдеу жазуға болмайды. Гормониялық осцилятор үшін потенциалдық энергияның формуласын жазайық:
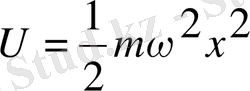 ;
;
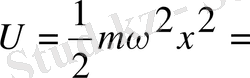
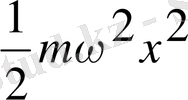 ; Потенциалдық энергияның операторы:
; Потенциалдық энергияның операторы:
3.
Классикалық физикада Гамильтон функциясы деп бөлшектің импульсі мен координа-талары арқылы өрнектелген толық энергияны айтады. Бір бөлшектің толық энергиясы кинети-калық және потенциалдық энергияларының қосындысына тең:
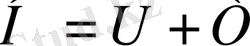
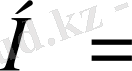
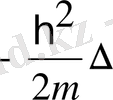
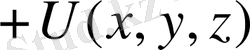

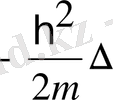
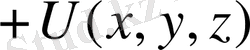 , осыдан
, осыдан
4.
Шредингер теңдеуін мына түрде жазамыз :
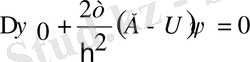 енді осыны
енді осыны
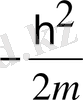 - ге көбейтелік, сонда:
- ге көбейтелік, сонда:
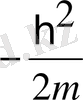
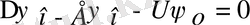
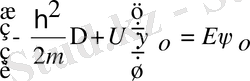
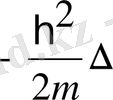
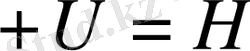 екенін ескерсек, сонда
екенін ескерсек, сонда
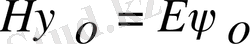
оператор түріндегі Шредингер теңдеуі. Бұл формуланы
 формула-сымен салыстырамыз. Сонда Шредингер теңдеуі Гамильтон операторының өздік функциясы мен өздік мәнін іздейді.
формула-сымен салыстырамыз. Сонда Шредингер теңдеуі Гамильтон операторының өздік функциясы мен өздік мәнін іздейді.
Тақырыбы: Де Бройль толқыны .
Лекция жоспары:
- Де Бройль гипотезасы.
- Де Бройль толқынының фазалық жылдамдығы
- Де Бройль толқынының дисперсиясы.
Жарық дегеніміз толқындық (интерференция, дифракция, поляризация), әрі корпускулалық (кванттық) қасиетке (фотоэффект, Комптон эффектісі) ие болатын өте күрделі процесс. Жарық толқындары ұзын болған кезде жарықтың толқындық қасиеті басым болады, оның кванттық қасиеті аз болады. Ал толқын ұзындығы қысқарған сайын кванттық қасиеттері әлсіз байқалады.
Жарықтың энергиясы, импульсі, массасы фотонда жинақталады. Бұл жарықтың кванттық қасиетін сипаттайды.
Француз физигі де Бройль (1924ж. ) корпускалалық-толқындық дуализм тек фотонға ғана тән емес, ол заттарды құрайтын бөлшектерге электрондарға тән болады деген болжам ұсынды.
Біртекті электрондар ағыны бар болсын, оның энергиясы Е, импульсі Р, тығыздығы тұрақ-ты
n=const
болсын. Мұндай электрондардың қозғалысын бейнелейтін толқындық функцияны қалай құраймыз. Фотон үшін:
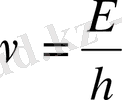 ;
;
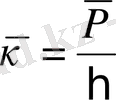 ;
;
 ~
~
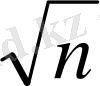 .
.
мұндай қатынас электрон үшін де орынды:
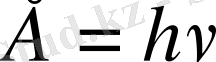 ;
;

Біртекті электрондардың ағынын бейнелейтін толқын монохроматты, жазық және тұрақты амплитудасы болу керек. Элементар бөлшектің қозғалысын сипаттайтын толқындық функция ψ арқылы белгіленеді.
 мұндағы:
мұндағы:
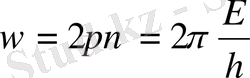 .
.
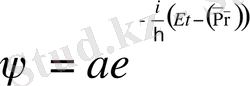 - бұл формула де Бройль толқыны деп аталады.
- бұл формула де Бройль толқыны деп аталады.
Де Бройль толқыны кеңістікте толқын заңдарымен таралады. Егер жолында кедергі кездестірсе, онда ол майысады (огибает) . Де Бройль гипотезасын айтқан кезде бірден қабылданған жоқ. Барлығы да электрондар - бөлшектер олар механика заңдарына бағынады деп айтылған. Де Бройльдың гипотезасын бекіту, қолдау керек болады. Ең жақсы дәлел олардың толқындық қасиетке ие екендігі болады. Электрон үшін дифракция құбылысы байқалу керек, сондықтан да осы құбылысты бақылайтын тәжірибе бақылаушы керек болады.
2. Әрбір толқын фазалық жылдамдықпен сипатталынады. Фазалық жылдамдық - бұл толқын фазасының жылдамдығының ауысуы. Толқын ұзындығы:
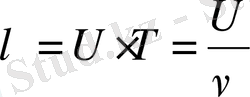 мұндағы:
U
- фазалық жылдамдық
мұндағы:
U
- фазалық жылдамдық
 фазалық жылдамдықты мына параметрлер арқылы жазуға болады: Е және Р;
фазалық жылдамдықты мына параметрлер арқылы жазуға болады: Е және Р;
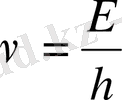 ;
;
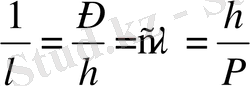 . Орнына қойсақ
. Орнына қойсақ
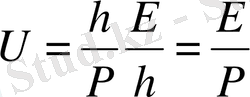 . Салыстырмалық теория бойынша
. Салыстырмалық теория бойынша
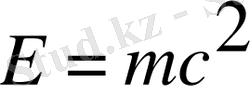 ;
;
 ;
;
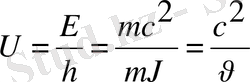 немесе
немесе
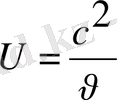 - фазалық жылдамдық.
- фазалық жылдамдық.
 , сондықтан
, сондықтан
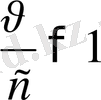 онда
онда
 электрон үшін
электрон үшін
 фотон үшін фазалық жылдамдық
фотон үшін фазалық жылдамдық
 .
.
Материяның ешқандай түрі жарық жылдамдығынан үлкен жылдамдықпен қозғала алмайды. Ал фаза жарық жылдамдығынан үлкен жылдамдықпен қозғалады. Де Бройль толқыны материалды емес, бірақ толқын материяның қозғалыс заңын береді.
3. Дисперсия - бұл толқынның құрамдас бөлігіне бөлінуі. Ол белгілі бір ортада ғана орынға ие болады. Мысалы, вакуумде дисперсия жоқ кезінде, фазалық жылдамдық жиілікке тәуелділігін табайық. Бұл байланыс де Бройль толқынының дисперсиясын береді
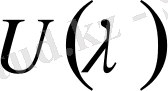 . Фазалық жылдамдық:
. Фазалық жылдамдық:
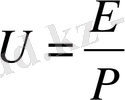 (1) .
(1) .
Бұл формуланы түрлендірелік
 (2) . Импульсін энергия арқылы жазамыз салыстыр-малық теорияда дәлелденеді:
(2) . Импульсін энергия арқылы жазамыз салыстыр-малық теорияда дәлелденеді:
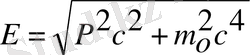
Кванттық теорияға келтіреміз:
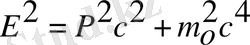 осыдан Р-ны табамыз:
осыдан Р-ны табамыз:
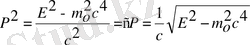 (3)
(3)
(3) - ші өрнекті (1) - ші өрнекке қойсақ:
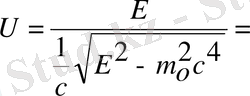
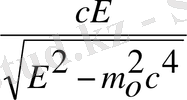 Е-ге бөлсек,
Е-ге бөлсек,
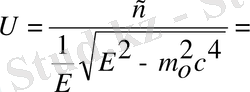
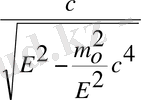
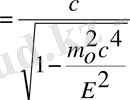 .
.
(2) -ші өрнекті ескерсек:
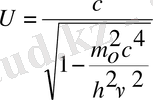
Бұл формуладан U ν-ға тәуелді екені көрінеді. ν -дан басқа барлық шамалар тұрақты.
Тақырыбы : Қозғалыс интегралы.
Лекция жоспары:
- Қозғалыс интегралы.
- Эренфест теоремасы.
1.
Егер оператордан алынған туынды нольге тең болса, онда оператор
қозғалыс интегралы
деп аталады.
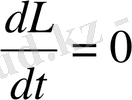 онда,
онда,
 - қозғалыс интегралы. Оператордың толық туындысы:
- қозғалыс интегралы. Оператордың толық туындысы:
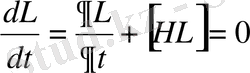 (1)
(1)
Егер оператор уақытқа тәуелді болмаса, онда
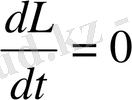 ;
;
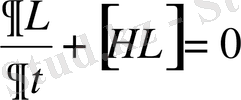 қозғалыс интегралының Пуассон жақшасы нольге тең.
қозғалыс интегралының Пуассон жақшасы нольге тең.
 -
-
 және
және
 операторының комутантымен анықталады. Егер H, L операторлары коммутативті болса, онда уақытқа айқын тәуелсіз кез келген L шамасы қозғалыс интегралы бола алады.
операторының комутантымен анықталады. Егер H, L операторлары коммутативті болса, онда уақытқа айқын тәуелсіз кез келген L шамасы қозғалыс интегралы бола алады.
Қозғалыс интегралының түрі бөлшек қозғалатын күшті күшпен өрістің табиғатына тәуелді. Еркін бөлшек үшін күш функциясы:
 . Сондықтан
. Сондықтан
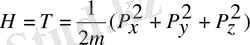
Классикалық механикадағы сияқты қозғалыс интегралы, яғни сақталатын импульс болып табылады.
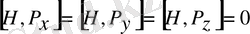 - қозғалыс интегралы сақталатын шама.
- қозғалыс интегралы сақталатын шама.
Импульс моментінің операторының қасиетін қарастырған кезде:
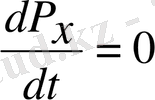 ,
,
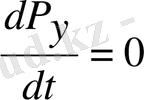 ,
,
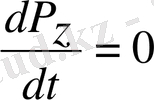
 және
және
 коммутативті екенін көрдік. Сондықтан
коммутативті екенін көрдік. Сондықтан
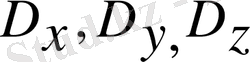 - қозғалыс интегралдары.
- қозғалыс интегралдары.
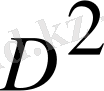 - импульс моментінің операторының квадраты да қозғалыс интегралы болып табылады:
- импульс моментінің операторының квадраты да қозғалыс интегралы болып табылады:
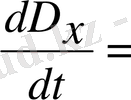
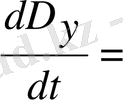
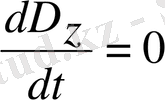 .
.
Егер (1) - ді Гамильтон операторына қолдансақ:
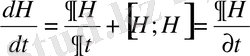 . Егер
. Егер
 уақытқа айқын тәуелді болмаса уақытқа тәуелді емес күш өрісіндегі толық энергия қозғалыс интегралы болады.
уақытқа айқын тәуелді болмаса уақытқа тәуелді емес күш өрісіндегі толық энергия қозғалыс интегралы болады.
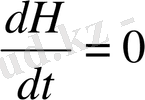 осы формула кванттық механикада энергияның сақталу заңын өрнектейді.
осы формула кванттық механикада энергияның сақталу заңын өрнектейді.
2. Координатаның және импульстің өзгеру заңын уақыт бойынша табамыз. Импульс және координата уақытқа айқын тәуелсіз шамалар болып есептеледі. Сондықтан оператордың уақыт бойынша алынған туындысы Пуасонның кванттық жақшасы арқылы өрнектейді.
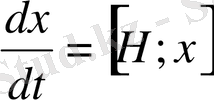 ,
,
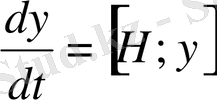 ,
,
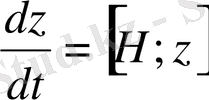 (1)
(1)
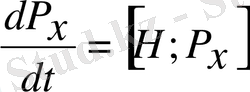 ,
,
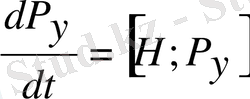 ,
,
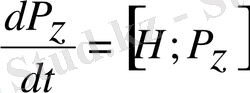 (2)
(2)
Бұл операторлық теңдеулер Гамильтонның классикалық теңдеумен сәйкес, сондықтан да
Гамильтонның кванттық теңдеуі
деп аталады. Классикалық механикада теңдеудің 1-ші тобы жылдамдықпен импульс арасындағы байланысты тұрақтандырады, ал 2-ші топ импульстің уақыт бойынша өзгерісін өрнектейді. Гамильтонның кванттық теңдеуі де осындай мәнге ие бұған көз жеткізу үшін Пуассон жақшасы айқын шешу керек. Гамильтон операторын проекция арқылы өрнектейік:
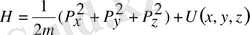


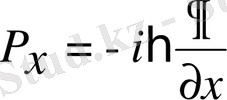 ;
;
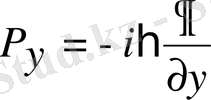 ;
;
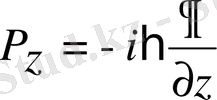
Бұл өрнектерді (1) -ші және (2) -ші формулаларға қойып:
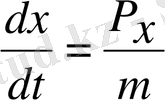 ;
;
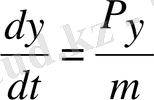 ;
;
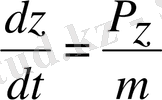 жылдамдықтың операторы импульстің операторын бөлшектің массасына бөлгенге тең.
жылдамдықтың операторы импульстің операторын бөлшектің массасына бөлгенге тең.
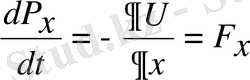 ;
;
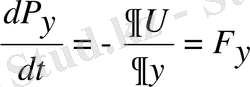 ;
;
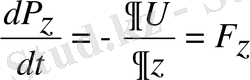 .
.
Импульс операторынан уақыт бойынша алынған туынды күш операторына тең. Егер
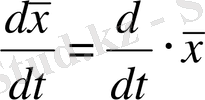 шамасының орташа мәнін есептесек ашылған түрде алатынымыз:
шамасының орташа мәнін есептесек ашылған түрде алатынымыз:
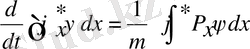 ;
;
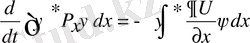
Бұл өрнектер Эренфест теоремасы деп аталады.
Тақырыбы : Таңдау ережесі.
Лекция жоспары:
- Таңдау ережесі.
- Гормониялық осцилятор үшін таңдау ережесі.
1. Система ψ і күйде болсын және оның энергиясы Е і . Бұл система ψ к күйге ауыссын және Е к энергияға ие болсын. Ауысу ψ і → ψ к ; Е і > Е к . Егер мұндай ауысулар бар болса, онда энергия айырымы қайда кетеді?
Бұл энергия айырымы сәулеленеді
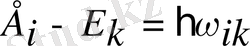 мұндағы:
мұндағы:
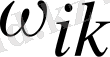 -
і
- ден
к
-ға көшкендегі сәулеленудің жиілігі. Егер мұндай ауысу бар болса, онда
-
і
- ден
к
-ға көшкендегі сәулеленудің жиілігі. Егер мұндай ауысу бар болса, онда
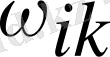 спектрде байқалуы керек. Егер бұл ауысулар жиі болса, онда спектр сызықтары ашық (күшті), ал сирек болса, онда спектр сызықтары әлсіз, сипаттайтынын көреміз. Энергияның мәнін біле отырып сызықтардың ин-тенсивтілігін есептеуге болмайды. Ауысу ықтималдығы белгілі болса, онда спектр сызық-тарының интенсивтілігін есептеуге болады.
N
i,
E
i
деңгейінде электрон орналассын атомдар саны
Е
к
деңгейіне ауысатын атомдар ғана
спектрде байқалуы керек. Егер бұл ауысулар жиі болса, онда спектр сызықтары ашық (күшті), ал сирек болса, онда спектр сызықтары әлсіз, сипаттайтынын көреміз. Энергияның мәнін біле отырып сызықтардың ин-тенсивтілігін есептеуге болмайды. Ауысу ықтималдығы белгілі болса, онда спектр сызық-тарының интенсивтілігін есептеуге болады.
N
i,
E
i
деңгейінде электрон орналассын атомдар саны
Е
к
деңгейіне ауысатын атомдар ғана
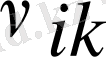 жиілігін сәулелендіреді сызықтық интенсивті-лігі:
жиілігін сәулелендіреді сызықтық интенсивті-лігі:
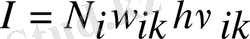 . Мұндағы
. Мұндағы
 - ауысу ықтималдығы
Е
к
энергиясына ие атомдар саны ста-тистика заңы мен анықталады. Егер
- ауысу ықтималдығы
Е
к
энергиясына ие атомдар саны ста-тистика заңы мен анықталады. Егер
 -ң мүмкін барлығын алсақ спектрдің кейбір жиілік-тері көрінбейді. Мұны былай түсіндіруге болады. Егер спектрде қандай да бір жиілік байқал-маса, онда оның ауысу ықтималдығы нольге тең екенін, ал қандай ауысудың ықтималдығыноль-ге тең емесін білу керек. Бұл қандай ауысулар мүмкін екендігін, қандай ауысулар мүмкін емес-тігін білдіреді. Өрістің кванттық теорияда ауысу ықтималдығы қорытылады. Ықтималдық мынаған тең екенін көрсетуге болады:
-ң мүмкін барлығын алсақ спектрдің кейбір жиілік-тері көрінбейді. Мұны былай түсіндіруге болады. Егер спектрде қандай да бір жиілік байқал-маса, онда оның ауысу ықтималдығы нольге тең екенін, ал қандай ауысудың ықтималдығыноль-ге тең емесін білу керек. Бұл қандай ауысулар мүмкін екендігін, қандай ауысулар мүмкін емес-тігін білдіреді. Өрістің кванттық теорияда ауысу ықтималдығы қорытылады. Ықтималдық мынаған тең екенін көрсетуге болады:
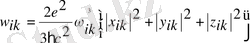
мұндағы
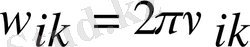
Егер ауысудың барлық матрицалық элементтері нольге тең болса, ауысу ықтималдығы нольге тең болады. Егер бір матрицалық элемент нольден өзгеше болса, матрицалық элемент кванттық санға тәуелді.
2. х осімен қозғалатын гормониялық осциляторды қарастырайық. у және z координаттары жоқ болсын. Таңдау ережесі 1-ші матрицалық элемент үшін алынды:
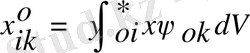
Гормониялық осцилятор үшін
х
-тең ξ-ге . Сондықтан
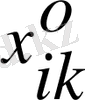 матрицалық элемент орнына
матрицалық элемент орнына
 матрицалық элементті іздейміз.
матрицалық элементті іздейміз.
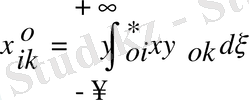 (1)
(1)
Гормониялық осцилятор функциясын интегралдаймыз:
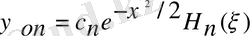
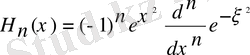
Функция заттық, сондықтан
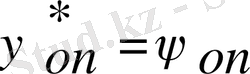 сонда
сонда
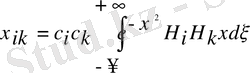 (2)
(2)
Полиномның біреуін анық емес түрде қалдырамыз. Ал олардың біреуін анық түрде жазамыз. Сонда
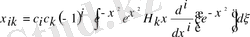 (3)
(3)
Бөліктеп интегралдаймыз, сонда

Мұндағы: 1-ші нольге тең осындай бөліктеп интегралдау і рет орындаймыз. Әрбір интегралдап шыққан мүше нольге тең. і рет интегралдағаннан кейін
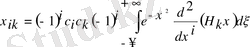 (5)
(5)
(-1)
і
- таңбаға байланысты қойылады.
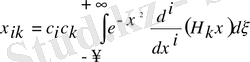 (6)
(6)
Керісінше істеуге де болады. Н
к
полиномы анық түрде, ал Н
і
анық емес түрде жазамыз. Сонда (6) формула
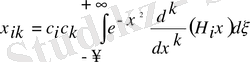 . (6
/
)
. (6
/
)
(6) формуланы қарастырайық. (6) формуладағы өрнекті дифференциалдаймыз.
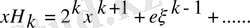 бұл өрнекті
і
рет дифференциалдаймыз. Полиномдағы үлкен мүше
бұл өрнекті
і
рет дифференциалдаймыз. Полиномдағы үлкен мүше
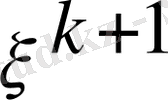 . Нөльді алу үшін
і≤к+1
егер бұл теңсіздік орындалмаса онда біз нольді аламыз (6
/
) формуланы қарастырайық. Мұнда полиномдағы үлкен мүше
. Нөльді алу үшін
і≤к+1
егер бұл теңсіздік орындалмаса онда біз нольді аламыз (6
/
) формуланы қарастырайық. Мұнда полиномдағы үлкен мүше
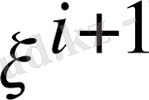 . Оны
к
рет дифферен-циалдау керек. Ноль болмау үшін мына теңсіздік орындалуы керек:
к ≤ і +1
2 теңсіздік алдық. Теңсіздікті шешеміз
к-1≤
і≤к+1
ноль болмау үшін бұл 3 жағдайда болуы мүмкін.
. Оны
к
рет дифферен-циалдау керек. Ноль болмау үшін мына теңсіздік орындалуы керек:
к ≤ і +1
2 теңсіздік алдық. Теңсіздікті шешеміз
к-1≤
і≤к+1
ноль болмау үшін бұл 3 жағдайда болуы мүмкін.
1) і=к+1 2) і=к 3) і≤к-1
1)
і=к; (
6
)
формула
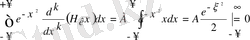
ξ кк =0 сондықтан і=к
2)
i=k+1
;
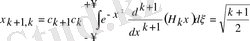 (7)
(7)
3)
і≤к-1;
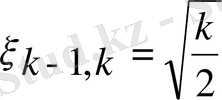 (8) . (7) мен (8) -ді бір формулаға біріктіруге болады.
(8) . (7) мен (8) -ді бір формулаға біріктіруге болады.
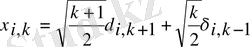 δ
ік
=1
болғанда
к=i
болады.
δ
ік
=1
болғанда
к=i
болады.
δ
ік
=0
болғанда
к
 i
болады.
i
болады.
i -бастапқы күйдегі кванттық сан, k - соңғы күйдегі кванттық сан.
Қорытынды: кванттық сан +1 ден -1-ге дейін өзгеретін кездегі ауысулар мүмкін болады.
Гормониялық осцилятордың энргетикалық деңгейінің схемасын салайық. (1-сурет) .
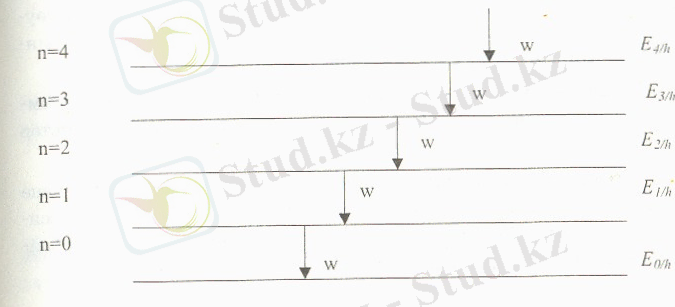
1-сурет. Гормониялық осцилятордың энергетикалық деңгейлері.
Көрші деңгейлермен ауысу болады. Ауысу кванттық сан 1-ге дейін азайғанда сәулелену болады. Кванттық сан 1-ге өскенде ауысуда жұтылу болады. Осцилятор бір ғана ω жиілігінде жұтылады және сәулеленеді.
Тақырыбы: Спиндік функциялар
Лекция жоспары:
- Спиндік функциялар.
- Паули теңдеуі.
Кванттық механикада спиннің күйі екі шамамен сипатталады. Бұлар спиннің кез келген бағыттағы проекциясы және спиннің квадраты. Спиннің квадраты барлық электрон үшін бірдей болады. Сондықтан біз айнымалы S z - ті ғана айтуға болады, яғни 3 айнымалымен қатар электронның ауырлық центрін анықтайтын тағы бір айнымалы S z пайда болады. Оның үшеуі электронның ауырлық центріне, ал 4-сі S z спиніне жатады. Сонда спиндік функция ψ=ψ(x, y, z, S z )
Егер функция уақытқа тәуелді болса
ψ=ψ(x, y, z,
S
z
t)
. Спиндік айнымалы тек екі мәнге ие сондықтан бір функцияның орнына 2-ші функция аламыз
ψ
1
=ψ(x, y, z, +
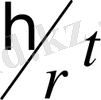 ), ψ
2
=ψ(x, y, z, -
), ψ
2
=ψ(x, y, z, -
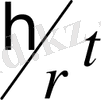 )
. Бұл функцияларды бір бағандағы матрица түрінде жазуға болады. Түйіндес функцияны бір қатардағы матрица түрінде келесідей жазамыз:
)
. Бұл функцияларды бір бағандағы матрица түрінде жазуға болады. Түйіндес функцияны бір қатардағы матрица түрінде келесідей жазамыз:
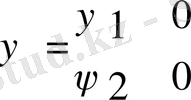
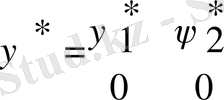
ψ
1
және ψ
2
функциясы әртүрлі болады, егер спині мен ауырлық центрінің қозғалысы арасындағы байланыс шын болса, мұндай байланыс спиннің магнит моментінің электронның ауырлық центрінің қозғалысын туғызатын тоқ магнит өрісімен әсерін сипаттайды. Бұл әсер спектр сызықтарының мультиплетін сипаттайды. Егер спектр структуралық мультиплетін ескерсек, онда
ψ
1
(x, y, z,
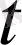 ) = ψ
2
(x, y, z,
) = ψ
2
(x, y, z,
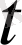 )
=
ψ(x, y, z,
)
=
ψ(x, y, z,
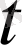 )
аламыз. Спині бар бөлшектің қозғалысын сипаттайтын толқындық функцияны ескеру үшін ондағы айнымалыларды алу керек.
)
аламыз. Спині бар бөлшектің қозғалысын сипаттайтын толқындық функцияны ескеру үшін ондағы айнымалыларды алу керек.
ψ(x, y, z,
S
z
t)
=
ψ(x, y, z,
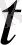 ) S
α
(S
z
)
) S
α
(S
z
)
S
α
(S
z
) -
спиндік функция деп аталады. α белгісі бөлшектің спинінің күшін көрсетеді және екі мәнді қабылдайды:
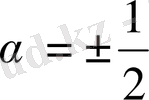 . Алғашқы мәні
. Алғашқы мәні
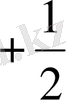 спиннің проекциясы
спиннің проекциясы
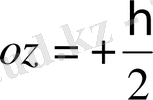 бағытын көрсетеді, ал 2-ші
бағытын көрсетеді, ал 2-ші
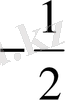 мәні спин проекциясы
мәні спин проекциясы
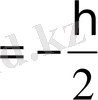 S
z
аргументін S
α
функциясын тәуелсіз айнымалы сияқты қарауға болады, ол да екі мән қабылдайды:
S
z
аргументін S
α
функциясын тәуелсіз айнымалы сияқты қарауға болады, ол да екі мән қабылдайды:
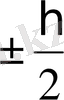 сонда
сонда
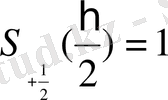 ;
;
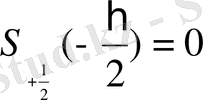
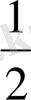 күйде 2 функция болуы мүмкін. Сонда
күйде 2 функция болуы мүмкін. Сонда
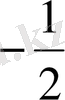 күйде
күйде
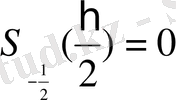 ,
,
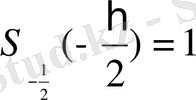 .
.
Келтірілген спиннің толқындық функциясы
S
α
(S
z
)
ортогональдық және нормалау қасиетіне ие. Кез келген спин операторының әсерінің нәтижесін есептейік:
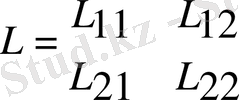
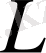 операторы ψ(ψ
1
ψ
2
) функциясынан жаңа φ(φ
1
φ
2
) функцияны жасайды. Ереже бойынша:
операторы ψ(ψ
1
ψ
2
) функциясынан жаңа φ(φ
1
φ
2
) функцияны жасайды. Ереже бойынша:
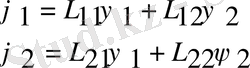
2. Кванттық механиканың негізгі теңдеуіне операторлық түрде жазалық
 (1) .
(1) .
 Гамильтон операторы. Егер спинді ескерсек осы спин үшін онда гамильтон операторына түзету енгізу керек. Система магнит өрісінде χ орналассын. Бұл системаның спиндік магнит моментін М
(S)
бар болсын. Осы моменттің арқасында электрон магнит өрісінде қосымша потенциалдық энергия алады, ол энергия дипольдік магнит энергиясына тең:
Гамильтон операторы. Егер спинді ескерсек осы спин үшін онда гамильтон операторына түзету енгізу керек. Система магнит өрісінде χ орналассын. Бұл системаның спиндік магнит моментін М
(S)
бар болсын. Осы моменттің арқасында электрон магнит өрісінде қосымша потенциалдық энергия алады, ол энергия дипольдік магнит энергиясына тең:
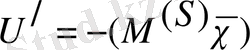 . Егер магнит өрісін z осі бойынша бағыттасақ, онда
. Егер магнит өрісін z осі бойынша бағыттасақ, онда
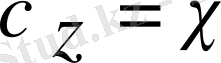 ,
,
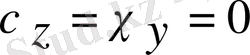 ,
,
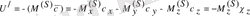 . Гамильтон операторын мына түрде береміз:
. Гамильтон операторын мына түрде береміз:
 (2) мұндағы
(2) мұндағы
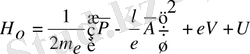 -Гамильтон операторы. Спинді ескергенде электромагниттік өрістегі зарядталған бөлшектің қозғалысы үшін: енді бұған потенциалдық энергияны қосу керек. Ол былай анықталады:
-Гамильтон операторы. Спинді ескергенде электромагниттік өрістегі зарядталған бөлшектің қозғалысы үшін: енді бұған потенциалдық энергияны қосу керек. Ол былай анықталады:
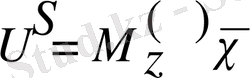 мұндағы:
мұндағы:
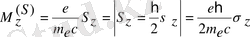 сондықтан
сондықтан
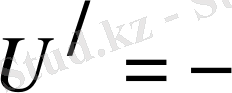
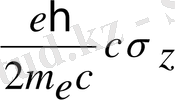 . Бұл операторды (2) формулаға енгізу керек.
. Бұл операторды (2) формулаға енгізу керек.
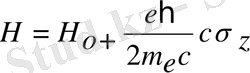 (3) . (3) -ші өрнекті (1) ші өрнекке қоямыз.
(3) . (3) -ші өрнекті (1) ші өрнекке қоямыз.
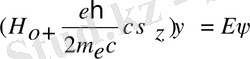 - бұл өрнек Паули теңдеуі деп аталады. Мұндағы
- бұл өрнек Паули теңдеуі деп аталады. Мұндағы
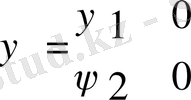
Сондықтан Паули теңдеуі екі теңдеудің жиынын құрайды. Мұнда толқындық функция ψ 1 және ψ 2 кіреді. Теңдеудің сол жағында матрица бар, сондықтан Гамильтон операторы матрицаны сипаттайды.
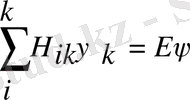
Бұл формуладан Паули теңдеуінің анық түрін анықтаймыз. Ол үшін белгілерге мән береміз.
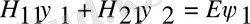
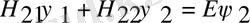 (4)
(4)
Бірлік матрицаның түрі
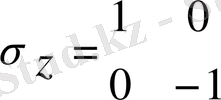
мұндағы:
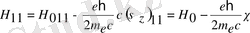
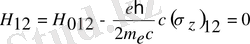
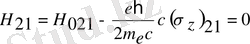
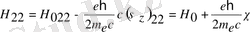
Бұл формулаларды (4) -ке қоямыз
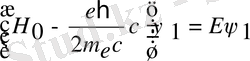 Паули теңдеуінің анық түрі.
Паули теңдеуінің анық түрі.
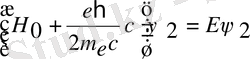
Тақырыбы: Ажырамаушылық принципі .
Лекция жоспары :
- Ажырамаушылық принципі.
- Симметриялы және антисимметриялы күйлер.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz