Физикадан шығармашылық есептер

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 34 бет
Таңдаулыға:

Қазақстан Республикасының білім және ғылым министрлігі
Ы.Алтынсарин атындағы Арқалық Мемлекеттік Педагогикалық институты

Мазмұны:
Кіріспе.
I тарау.
Есеп шығарудың теориялық негіздері.
§1.1 Физикадан есеп шығарудың маңызы , мәні .
§ 1.2. Әр түрлі типтегі есептерді шығару жолдары.
§ 1.3. Физикадан шығармашылық есептер.

II тарау.
Физика есептерін шығаруда индукция әдісін қолданудың
әдістемелік
негіздері.
§ 2.1. Орта мектепте физика есептерін шешуде индукция әдісін
пайдалану.
§ 2.2. Физика есптерін шығару әдістерін жетілдіру түрлері.

III тарау.
Практикалық іс – тәжірибе.
§ 3.1.Идеал газ күйінің теңдеуі.
Қорытынды.
Пайдаланылған әдебиеттер.
Қосымша материалдар.

Кіріспе.
Қазіргі педагогика ғылымының алдында тұрған міндет , оқушыларға
белгілі бір білім жүйесін беріп қана қоймай , олардың әрқайсысының
шығармашылық қабілетін айтарлықтай дамыту болып табылады.
Қазіргі физиканы оқыту әдістемесі оқушының танымдық қызметі мен ойлау
жүйесінің арақатынасын айқындай түсуде. Ол оқушының дербестігін ,
танымдық қажеттілігімен , интелектуальдық ойлау мүмкіндіктерін
қалыптастырады.
Мектеп курсында физикадан есеп шығару – оқу жұмысының қажетті
элементі. Мектептегі физика пәнін оқытудың негізгі мендеттеріне
оқушыларға білім жүйесін меңгертіп қоймай , олардың логикалық ойлау
қабілетін қалыптастыру жатады. Сонымен қатар , оқытудың аса маңызды
міндеттерінің бірі ғылыми зерттеулерде қолданылатын әдістер туралы
түсінік беру , бұл әдістерді меңгеруге жәрдемдесу болып табылады.
Физика есептерін шешудің үлкен білімділік , дамытушылық , тәрбиелік
мәні бар екендігі бәрімізге мілім. Мазмұны бай , терең білімге
лайықтап құрылған , кішігірім ғылыми проблема тәрізді есептерді
шешіп , есеп мазмұнында келтірілген физикалық құбылыстарды жан – жақты
талдап , оның ерекшеліктеріне тоқталып , тиісті баға беру әдістемелік
жағынан ұтымды болады.
Мектеп оқушыларының бақылау мен аналогия , индукция , тәжірибеге
арналған есептер оқцшылардың эвристикалық қабілетін дамыту үшін
маңызы зор.
Менің дипломдық жұмысымның негізі , физика есептерін шешуде
индукция әдісін қолдану жолдары.
Зерттеу объектісі - индукция әдісін физика есептерін шешуде
қолдану жолдары.
Зерттеу мақсаты - индукция әдіс – тәсілін физика сабағында
қолданудың тиімді жолдарын анықтау.
Жоғарыда көрсетілген жұмыстың мақсатына жету мынадай
міндеттер қойылады :
1) Есеп шығарудың бір тәсілі - индукция тәсілін физика
сабақтарында қолдану жолдарын анықтау.
2) Сабақтарда индукциялық тәсілді қолданудың жүйесін ұсыну.
3) Индукциялық тәсілді қолданудың тиімділігін тексеру
жөнінде педагогикалық эксперимент өткізу.
Осы көрсетілген есеп шығару жетісдірілген әдісті (
Индукция әдісі , т. б. ) пайдаланудан біздің дипломдық жұмысымыздың
маңыздылығы шығады.

I – тарау. Есеп шығарудың теориялық негіздері.
§1 .1. Физикадан есеп шығарудың маңызы мен мәні.

Оқыту , мұғалімнің ерекше бағдарлы мақсат көздейтін қызметі
ретінде , оқушыларды біліммен , іскерлікпен , дағдылармен және
оларды танымдық , творчестволық қабілетпен қаруландыратын кең
мағынасындағы тәрбиенің біртұтас маңызды бөлігі болып табылады.
Оқу практикасында физикалық есеп деп , жалпы жағдайда логикалық
ой қорыту , матеметикалық амалмен физика заңдары және әдістері
негізіне сүйенетін , эксперимент көмегімен шешілетін өте зор емес
проблеманы атайды.
Есептер қандай да бір нақты жағдайда болып өтетін
құбылыстарға физикалық заңдылықтарды қолдануды талап ететін
жаттығулар үшін материал береді. Сондықтан олардың әрқайсысы
оқушылардың білімін нақтылауда , далпы эаңдардың түрлі көрінісін көре
білуде , дамытуда үлкен маңызы бар . Мұндай нақтылаусыз
білімдердің практикалық бағасы болмайды. Есептер шешу физикалық
заңдылықтарды тереңірек және берік меңгеруге , логикалық ойлаудың
дамуына , ұғымды және инициативалы болуға , ерік және қойылған
мақсатқа жетудегі табандылыққа көмегін тигізеді , физикаға
қызығушылығын оятады , өзіндік жұмыс дағдыларын бойына сіңіруге
көмектеседі және өзіндік ой қорытуда бірден – бір құрал болып
табылады.
Есептер шешу процесінде кейде сабақта жаңа ұғымдар мен
формулалар енгізуге , оқып үйренілетін заңдылықтарды түсіндіру ,
жаңа материалдың мазмұнына жақындата түсуге болады.
Физикалық есептің мазмұны оқушылардың табиғат пен техника
жөніндегі білім шеңберФизикалық есептің мазмұны оқушылардың табиғат
пен техника жөніндегі білім шеңберін кеңейтеді , оларды практикада
қолдана білуге үйретеді. Оқушылар есептерді шығарғанда тікелей
физикадан алған білімдерін қолдану қажеттілігімен кездеседі ,
теория мен практиканың байланысын тереңірек сезінеді.
Есеп шығару - қайталауды , пысықтауды және оқушылардың алған
білімдерін тексерудің бірден - бір құралына жатады.
Физика есептерін шешу дегеніміз нені білдіреді ? Бір
қарағанда бұл сұрақ оңай болып көрінуі мүмкін : есепті шешу
дегеніміз - оның жауабын табу . Бірақ ойлай келе , есептің жауабын
табу , оны шешуге жатпайтындығына көз жеткізуге болады , өйткені ,
жауап көбіне алдын - ала белгілі , есепті шешпей -ақ оқулықтың
немесе есеп кітабының соңғы парақтарынан табуға болады.
Есепті шешу – тек қана оның жауабын тауып қою ғана емес , одан
гөрі маңыздырақ , күрделірек нәрсе.
Физикалық есепті шешу барысын неден тұратындығына көз жеткізу
үшін , келесі есептердің шешуін табайық ( қарастырайық ) :
Есеп 1. Материялық нүктенің үдеуі
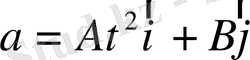
заңымен өзгереді. Мұндағы А=2 мc2 , B=3 мc2 . Егер материялық
нүктенің уақыт t0=0 болғандағы бастапқы жылдамдығы V0=0 және
радиус – векторы r0=0 , болса , онда t уақыт өткеннен кейін оның
координаттары бас нүктесінен қашықтығын анықиаймыз :
Берілгені :

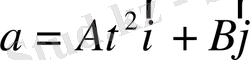
A= 2 мc2
B = 3 мc2
t0=0 , V0=0 , r0=0
t= 1c
__________________________
r = ?

Шешуі : есептің шарты бойынша нүктенің r= r(t) қозғалыс заңы
анықтап , сол бойынша t= 1c болғандағы шамасын табуымыз
керек. Ол үшін әуелі үдеудің өрнегінен жылдамдықты тауып
алу керек , сонда немесе . Соңғы теңдікті есептің
шарты бойынша берілген үдеудің өрнегімен салыстырып :
(1)
болатынын көреміз . (1) өрнекті интегралдау нәтижесінде
Х және У осьтері бойындағы проекцияларын аламыз :

(2) Бастапқы жылдамдықтары t0=0 болғанда Vx=0 , Vy=0
болғандығын еске алсақ , онда С1=1 және C2= 0 екендігін
анықтаймыз , ендеше (2) өрнекті былай жазамыз :
, (3)
Осы (3) өрнекті интегралдау нәтижесінде мынаны анықтаймыз :
, (4)
Жоғарыдай бастапқы шартты еске алсақ С3=0 , С4=0 болып
шығады. Олай болса қозғалыстың теңдеуі мына түрге келеді :
(5)
(5) өрнектен t= 1с болғандағы шамасының модулін
табамыз:
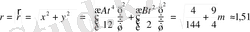м.
Физикалық есепті шешу дегеніміз - есептің шарттарын және
шешу барысында аралық нәтижелерін қолдана отырып , ақырғы
қорытындысында есептің талабын қанағаттандыратын физиканың жалпы
теориялық жайларының (анықтамаларының т.б. ) тізбегі мен
математикалық операцияларды табу.
Әрине , бұл анықтама физикалық есепті шешу барысының ең
маңызды жерлерін көрсетеді. Есепті шешу барысында басқа да
көптеген жұмыстарды орындауға тура келеді , мысалы , санақ системасын
, координаталар системасын таңдау , құбылыстың системасын жасау (құру)
және т. б.
Әрбір сәтті құрылған есептерді шешуді қарастыру , өнер табу
мен ғылыми жаңалық ашудың сан алуан қиын да , әрі қызықты
жолдарын үйретуге арналған ұтымды методикалық әдістердің қарарына
жатады.
Физикалық есептерді шешу – оқушылардың ойлау мен шығармалық
қабілетін дамытатын басты құралдардың бірі. Көп жағдайда
құбылыстарға байланысты проблемалық жағдайлар , физикадан есептер
шығару барысында туады да, бұл оқушылардың пәнге деген
белсенділігін , қызығушылығын арттырады. Сонымен бірге физикалық
есептерді жүйелі түрде шығарта отырып , оқушылардың алған білімін
тексеруге және де еске түсіруге болады. Сондықтан физикалық
есептерді жүйелі шығарып отыруға мұғалім баса назар аудару қажет.
Көрнекті әдіскер Д. Пойя : есеп шығара білу - бұл
практикада қалыптасатын өнер - деген еді. Расында суда жүзу
туралы қанша көп оқығанымен , суда жүзіп көрмей , жүзуді үйрену
мүмкін емес . Демек , есептерді де жүйелі түрде шығармай ,
теорияны жақсы меңгеру мүмкін емес. Алайда , мынаны еске
сақтаған жөн : есепті шығарып қана қою мақсат емес , ең бастысы
есеп шығара отырып , физикалық білімдердің жаңа сатысына көтерілу
, белгілі бір мақсатты жинақтап , ойлануға үйрену. Қорыта айтқанда
, мазмұны қарама - қайшылықтар мен конфликтілік жағдайларға
лайықтап құрылған есептерді шешу , оқушыларды ой алғырлығына
тәрбиелеп , инемен құдық қазғандай ғылым жолына түсуге
көмектесері сөзсіз.
Физикадан есеп шығару – оқу жұмысының қажетті элементі.
Есептер шығару физикалық заңдарды тереңірек және берік меңгеруге,
логикалық ойлаудың дамуна, ұғымдылық , инициативалы болуға , ерік және
қойылған мақсатқа жетутегі табандытыққа себі тиеді., физикаға қызығушылығын
оятады, өзіндік жұмыс дағдыларын бойына сіңіруге көмектеседі және өзіндік
ой қорытуда бірден – бір құрал болып табылады.
Есептер шығару – қайталауды , пысықтауды және оқушылардың білімін
тексерудің маңызды құралы.
Шығару тәсілдеріне қарай сандық есеп , сапалық есеп , эксперименттік
есеп деп бөлінеді. Солардың біреуі ретінде өз тәжіребемнен мысал
келтірейін. Анықтап айтқанда , қатты денелердің қысымы тақырыбына VIII –
сыныпта есептер шығару мәселесіне тоқталамын.
Сандық есептер.
№1. мұз 8 Н\см қысымға шыдайды. Массасы 3000 кг , тіреу ауданы 800 см
автомобиль осы мұздан өте ала ма?
А . Жоқ ; Б. Ия; В. Дұрыс жауабы жоқ.
№2. Мыналардың қайсысы көп қысым түсіреді ? Массасы 60 кг , тіреу
ауданы 160 см адам ба , әлде массасы 10 т шынжыр табанының тіреу ауданы 2м
шынжыр табанды трактор ма?
А. Адам, Б. Трактор ; В. Екеуі де бірдей қысым түсіреді.

Сапалық есептер.
№3. Адам еденде тыныш тұрғанда біршама қысым түсіріп тұрады. Сол
қысымды екі есе көбейту үшін не істеу керек ?
А. Ол үшін секіру керек
Б. Қосымша жүк көтеру керек. В. Ол үшін бір аяқпен тік тұру керек,
себебі ауданды 2 есе кішірейтсек , қысым екі есе артады.
№5 Қысым дегеніміз не?
А. Дененің бетіне перпендикуляр бағытта әсер етуші күш ; Б. Берілген
дененің Жерге тартылу күші; В. Жердің тертылу салдарынан тіреуішке түсетін
күш.
№6. қысымның формуласын тап.
А. Р=mg ; Б. F= gm ; B. P =FS

Эксперименттік есеп.
Үстел үстінде тығыздығы белгілі кірпіш тасы жатыр. Тастың үстелге
түсіретін қысымын табу керек. Оның айдағы салмағы мен массасы қандай болмақ
?
Өлшеулер : тастың ұзындағын енін , биіктігін сызғыш арқылы
анықтаймыз.
Есептеулер : өлшенген үш шаманың көбейтіндісі бойынша көлемді ,
ұзындығы мен енінің көбейтіндісі бойынша ауданды есептейміз.
Белгілі тығыздық пен көлемді көбейту арқылы тастың массасын
анықтаймыз. Массасы 9,8 Hкг –ға көбейту арқылы қысым күшін табамыз.
Қысымды табу үшін қысым күшін тіреу тіреу ауданына бөлеміз.
Тастың айдағы салмағы Жерге қарағанда 6 есе кем, ал ал массасы Айда
өзгермейді.
Жауаптары : 1А,2Б,3В,4А,5В
Күнделікті сабақтарда есептерді шығарудың осындай тиімді тәсілдері
оқушылардың физика пәніне деген қызығушылығын арттырады.

§1.2. Есептер классификациясы және әртүрлі типтегі есептерді
шығару жолдары.

Физика есептері мазмұны және дидактикалық мақсаттарына сай
алуан түрлі . Оларды түрлі мазмұндағы көптеген есептер үшін
неғұрлым типтік қасиеттерін бейнелейтін әртүрлі бейнелеріне қарай
классификациялауға болады.
Бқл мәселені қарастырғанды есептерді классификациялау , басқа
ғылыми ұғымдар сияқты , әртүрлі белгілеріне қарай , классификациялау
мақсатына қарай жүзеге асыру керек . Атап айтқанда , есептер былай
классификациялануы мүмкін :
- ондағы информацияның берілу тәсілі бойынша;
- шығарудың негізгі тәсілі - есепте қойылған сұрақтың
жауыбын алу бойынша ;
- мазмұнына , бағытына , сұрақты зерттеу тереңдігіне , шешу
әдістеріне және т. б. байланысты.
Мазмұнына қарап есептерді , ең алдымен , олардың физикалық
материалына байланысты болу керек. . Есептер механика , молекулярлық
физика , электродинамика есептеріне бөлінеді . Мұндай бөлудің шартты
болуы , есептің талабында физиканың бірнеше бөлімінен мағлұматтар
пайдалануына байланысты .
Есептер абстракциялы және нақты мазмұндағы есептерге бөлінеді.
Абстрактылы есептердің ерекшелігі - оларда маңызсыз детальдер әсерін
тигізбейтін , физикалық маңызы анық көрінеді . Нақты есептер
ерекшелігі – айқын көрінерлігімен , өмірмен тығыз байланыстылығында .
Техника , өнеркәсіптік және ауылшаруашылықтық , өндіріс ,
транспортпен байланыс туралы материалдар жинақталған есептерді
политехникалық есептер деп атайды .
Политехникалық есептердің мазмұны , зерттеліп отырған
программалық материалмен тығыз байланыста болуы керек . Қарастырылып
отырған техникалық обьект немесе құбылыс , әдетте , ауылшаруашылығында
кең қолданылуы қажет . Есепте машиналар , процестер туралы шынайы
деректер және іс жүзінде кездесетін сұрақтар қойылуы керек.
Техникалық есептер мазмұнымен ғана емес , сонымен қатар түрімен ,
қалпымен өмірде кездесетін жағдайларға барынша сәйкес болуы керек .
Бірқатар есептер тарихи тұрғыдағы мәліметтерге йе : классикалық ,
физикалық , тәжірибелер , жаңалықтар немесе тарихи аңыздар туралы
есептер . Мұндай есептерді тарихи мазмұнды есептер дейді.
Кейбір жағдайда бірқатар есептерді шығарғанда жалпы тұрғыдан
айқындау мақсатында немесе шешудің алгоритмін құруды , есептерді
шығару тәсілдері бойынша классификациялау ыңғайлы . Есептерді онда
қамтылған информация бойынша классификациялай отырып , біз есептердің
шартының айтылу тәсіліне басты назар аударамыз.
Физикалық есептерді айтылу тәсіліне қарай , негізінен төрт түрге
бөлінеді : текстілі , эксперименттік , графиктік және сурет есептер .
Сұрақты зерттеу тұрғысында олардың әрқайсысы сандық ( немесе есептеу
) сапалық ( сұрақ есептер ) болып бөлінеді . Сонымен қатар есептің
негізгі түрлерін қиындық дәрежесіне қарай :оңай және қиын , жаттықтыру
есептері мен шығармашылық есептер және басқа да типтерге байланысты
бөуге болады.
Физиканы оқыту процесінде текстілі есептер жиірек пайдаланылады.
Бұл есептер шартты сөзбен берілген , дәлме - дәл , әрі олардың
шарттарында физикалық тұрақтылардан басқа барлық қажетті мәліметтер
бар есептер .
Шығару тәсіліне қарай оларды сұрақ есептер және есептеу
есептері деп бөледі .
Сұрақ есептер – бұл шығару кезінде қандай да бір физикалық
құбылысты түсіндіреді .( есептемеуду орындамай ) немесе белгілі бір
жағдайда құбылыстың қалай өтетіндігіне болжам жасауды қажет ететін
есептер . Мұндай есептерді шешу кезінде есептеулер жүргізілмейді.
Әдетте , мұндай есептер мазмұнында сан мәліметтері болмайды .
Есептеулердің болмауы оқушылардың назарын физикалық мәніне назар
аударуға мүмкін- дік береді.
Қойылған сұрақтарға жауаптарды негіздеу қажеттіг і , оқушыларды
пайымдауға , физикалық заңдардың мәнін тереңірек ұғынуға үйретеді.
Енді осы сұрақ – есептерге мысалдар келтірейік :
1) Сүрінген адам неге алдыға қарай құлайды ?
2) Киімді қаққанда шаңнан тазаруы қандай құбылысқа негізделген ?
3) Балтаны саптаудың қандай әдістері бар ? Олар қандай құбылысқа
негізделген ?
Үш есепте де инерция құьылысы орын алады , сондықтаан оқушылар
бұл есептерді кезінде , ой қорыту жүйесін жасағанда , берілген
құбылыстарды түсіндіретін физикалық заңға сүйенеді . Қарастырылып
отырған жағдайларға бұл Ньютонның бірінші заңы – инерция заңы , оның
формуласын оқушылар есепті шешу барысында қайталаулары қажет .
Инерция заңын қолдана отырып , сүрінген адам аяқтары бір
кедергіге ұсталатындықтан тоқтайды да , ал денесінің басқа мүшелері
инерциямен қозғала беретіндіктен алдыға құлайды деп ой қорытады .
Осыған ұқсас жолмен басқа да есептердің де сұрақтарына жауап береді
.
Сұрақ есептерде физикалық формулармен көрсетілген әртүрлі
тәуелділіктер де қолданылуы мүмкін .
Мысалы :
4) қандай әдіспен адам еденге түсірілген қысымды 2 есе көбейте
алады ?
Алдымен болып жатқан құбылыстың физикалық маңызына талдау
жасайды . Есепте қысым жайында сұралады , ал қысым Р қысым күші Ғ
модулінің сол күш әсер ететін S ауданға қатынасымен анықталады . Яғни
P=FS
Осыдан қысым қысым күшіне ғана емес , ауданға да байланысты
өзгеретіндігін көреміз .
Сондықтан , біріншіден , сол ауданға түсетін қысым күшін
екі есе арттырсақ , қысым да екі есе көбейеді . Мұны адамның өз
салмағындай жүкті қолға алып , көз жеткізуге болады . Бірақ екінші
мүмкіндік те бар , ол тірек ауданын екі есе кішірейту . Бұл үшін
адамға бір аяққа тұрса жеткілікті . Тепе - теңдік бұзылмас үшін ,
тұрған адам тұрысын сәл өзгертеді .
Сұрақ есептерді шығару есептің графиктік материалына байланысты ,
әдеттегідей ауызша орындалады . Жауаптар суреттермен де берілуі
мүмкін .
Сұрақ - есептер мен сурет -есептер тығыз байланысқан . Бұларда
сұраққа жауап ауызша болатын суретін салу талап етіледі . Мұндай
есептерді шығару оқушылардың зейінін , бақылағыштығын , т.б. дамытуға
көмектеседі.
Оқушыларда сұрақ - есептерді саналы тұрғыда шығару дағдысын
тәрбиелеу үшін , мұғалімнің олармен белгілі бір жұмыс жүйесі және
ойластырылған оқыту әдістемесі болуы керек . Есепті дұрыс таңдап
алдудың да маңызы зор. Есептің алғашқы кездерінде оқушылардың өз
тәжірибесінен белгілі құбылысқа немесе фактілерге беру туралы
ұсынылатын есептер дұрыс болады. Мұндай есептерден оқушылар өмірмен
байланысты көреді . Есептерді таңдап алуда мектептің айналасындағы
өндірістің сипатын және жергілікті жағдайларды ескерудің маңызы зор .
Сұрақ есептерді шығару үш кезеңнен тұрады : шартын оқу , есептің
анализі , шешуі .
Есеп мазмұнын анализдеу негізінде , ең алдымен оқушылар берілген
тақырыптан белгілі ортақ заңдылықтарды пайдаланады , осыдан кейін
есептегі айтылған құбылыс нақты қалай түсындірілуі тиіс екенін
айқындайды . Сұрақ есептерде шарттың анализі негізделген керекті
жауаппен тығыз байланысты .
Сандық есептер . Бұл есептерде қойылған сұрақтардың жауабын
есептецлерсіз алуға болмайды . Мұндай есептерді шығарғанда сапалық
анализ де қажет , бірақ оны процесті қандай да бір сандық
сипаттамаларды санау арқылы сапалық анализбен толықтырады. Сандық
есептер қиындығына қарай жай және күрделі болып бөлінеді.
Жай есептер деп , күрделі емес , анализбен жай есептеулерді қажет
ететін , әдетте , екі амалмен шығарылатын есептер түсініледі . Мұндай
есептерді шығару енді ғана оқып үйрекнілген заңдылықтарды нақтылау
үшін қажет. Олардың неғұрлым оңайларын ауызша шығаруға болады.
Сандық есептерді шығару үшін түрлі : арифметикалық , алгебралық ,
геометриялық , графиктік тәсілдер қолданылады.
Есеп шығарудың арифметикалық тәсілінде арифметикалық амалдар
қолданылады және есептеуі де шамамен есеп шығарғандағыдай. Мектептерде
қазіргі қолданылып жүрген көшкенімен , есептерді арифметикалық
тәсілмен шығару ,негізінен VII класта , кейде VIII кластарда да болады.
Бұл алгебраны оқып үйренуді бұрын тек VII кластың екінші жарты
жылдығында бастауға байланысты еді. Жаңа программаға көшумен байланысты
бұл мәселелерді шешу де өзгеруі мүмкін.
Есептерді шығарудың алгебралық тәсілі формулалармен теңлеулерді
қолданумен шектеледі.
Геометриялық тәсілде -геометриялық теоремалар , ал графиктік тәсілде
– графиктер пайдаланыланы.
Текістілі есептердің қатарына абстрактылы есептерді жатқызуға
ьолады , бұл күнделікті өмірде бақыланған құбылыстар мен процестер сөз
болатын есептер , өндірістік – техникалық мазмұнды есептер және
ақырында тарихи мазмұнды есептер. Кейде текстілі есептердің қаиарына
қызықты есептер делінетін ерекше топтағы есеептер жатады.
Есептердегі эксперимент түрліше қолданылады.
1) Кейбір жағдайда демонстрациялық үстелде жүргізілген
тәжірибеден немесе оқушылардың өздері орындаған тәжіребелерінен
есепьтер шығаруғы қажетті мәліметтерді тауып алады. Бұл жағдай – есепті
тәжірибесіз шығаруға болмайды.
2) Тағы бір жағдайларда есептің шартында көрсетілген
мәлімет- ге сүйеніп ,есепті тәжірибесіз де шығаруға болады. Мұндай
жағдайда есепте айтылған құбылыстар мен процестерді иллютрациялау үшін
немесе шешудің дұрыстығын тексеру үшін пайдаланады. Бірақ , егер
эксперимент тек қан есепті тексеру ұшін қолданылса , ондағы есепті
эксперименттік деп атау дұрыс болмайды.
Эксперименттік есепті шығару процесінді оқушылардың бақыла-
ғыштығы дамытылыда , приборлармен жұмыс істеудегі дағдылары
жетілдіріледі. Мұнда оқушылар физикалық құбылыстар мен заңдылықтар-
дың мәнін тереңірек танып біледі.
Күрделі сандық еспетерді шығару сабақта , әдетте , мына
элементтерден құралады :есептіің шартын оқу , шартты қысқаша жазу оны
қайталау , суретін , схемасын немесе чертежін салу , есептің физикалық
мазмұнын анализдеу және оны шығару жолдарын айқындау , шешу жоспарын
құру және жалпы түрдегі шешуін тексеру.
Күрделі есептерді келтірілген схемасын щқушылардың онің мазмұны мен
шығару барысын біртіндеп жан – жақты ойластыруын қамтамасыз етеді.
Есептерді шешуінің алгоритмдік деп аталатын түрі шешудің белгілі
осы арнайы жасалған , көрсетілген амалдарды ретімен орындайды. Бірақ бұл
тәсілді қолдану мектептерде кең қолдану тапқан жоқ , өйткені , алго-
ритмдердің көп санын жасау оларды еске сақтау керек болды.
Қазіргі кезде мектептердің барлық түріне қолдануға келетін ,
оларды шешудің жолын көрсететін физикалық есептердің шешуінің жалпы
әдістерін жасауға әрекеттер жүріп жатыр.
Физикалық есептердің шешуінің әртүрлі әдістерімен оқушыларды нақты
есептерді шешу барысында таныстыру керек. Физикалық заңдылықтарға
сүйене отырып , сандық есептерді шешудің жолы бар , әйтсе де
матаматикалық операцияларға тәуелді шешу тәсілдері бар. Олар :
алгебралық , математикалық , геометриялық , тригонометриялық , графикалық
тәсілдер.
Физикалық есептерді алгебралық тәсілмен шығаруды қарастырайық:

Есептерді бұл тәсілмен шешкенде формулаларды пайдалануды ,
алгебралық теңдеулерді құрай отырып , шешеді. Алгебралық тәсілдің
қолданылуының ең қарапайым түрі – да йын формуланы пайдаланып шешу.
Одан күрделірек есептерде ізденуді , тәуелділікті бірнеше формула
немесе теңдеулерді пайдаланып анықтайды.
Қазіргі кезде физика есептерін шешудің келесі әдістері
жинақталып, жалпы қабылданған : аналитикалық ,синтетикалық ,
аналитикалық – синтетикалық . бұл әдістер есептерді шешу кезінде
жасалынатын ойлау актілерінің сипаты мен тізбегін айқындап көрсетеді.
Есептердің шешуінің негізгі әдістерін және ойлау қызметінің
оларға сәйкесті түрлерін схемалық түрде көрсетуге болады. (1- сурет)
Есептердің кейбір түрлерін шешу барыснда , әдіскерлер ерекше бөліп
көрсетпесе де , аналогия деп аталатын әдіс өз жемісін береді.

Таза түрдегі аналитикалық және синтетикалық әдістер өте сирек
кездеседі , ал көбірек қолданылатын әдісі - бұл аналитикалық -
синтети- калық.
Жоғарыда келтірілген шешу әдістеріне бір қатар мысалдар
келтірейік .
Аналиттикалық әдіс .
Бұл әдісті қолдану барысында есептің талабынан ізделінді шама
бөліп алынады , содан кейін аналитикалық ой толқысы физикалық заңдар
немесе формулалар көмегімен қарастырылып отырған құбылыс немесе
процестің қандай шамалары ізделінді шамамен өзара байланысқандығы
айқындалады. Осыдан соң аралық шамаларды қарастырамыз , есептің
шартында олар анықталған ба , жоқ па ? Егер олар анықталмаған болса
, алдындағы характеристикалармен функциональді байланысқан басқа
шамаларды пайдалану процесін олар есеп шарттында берілгенге шейін
жалғастырамыз.
Біздің жағдайда аналитикалық ой талқылау тізбегі төмендегідей
болып көрсетілуі мүмкін :
1) Кабина троспен бірқалыпты үдемелі түсіп келеді. Қорытынды :
қозғалыс бағыты төмен қарай бағытталған , қозғалыс үдеуі
тұрақты.
2) Кабинаға төмен қарай бағытталған ауырлық күші әсер
етеді, тростың керілу күші (жоғары қарай
бағытталған ) . Қорытынды : кабинаның үдемелі қозғалысы
көрсетілген күштердің тең әсерлі күшімен анықталады.
3) Ньютоннның III – заңы бойынша үдеу кабинаға әсер ететңін
күштердің тең әсерлі күші пен оның массасы m арқылы
анықталады. Қорытынды : , одан
, сөйтіп ізделігді шама

4) Айқын берілмеген аралық шама үдеу - бір
қалыпты үдемелі қозғалыс заңынан табылады : жолдың қозғалыс
уақыты мен үдеуінен функциональді тәуелділік :
формуласымен анықталады. Осыдан :
,
бұл жерде - уақыт.
5) күштердің әсерлерінің және удеу бағытын ескере
отырып , мына түрдегі алгебралық теңдеуін ( физикалық есептің
математикалық моделін ) шығарамыз :
,
мұнда ізделінді шама есептің шартында
берілген шамалармен функциональді байланысқан.

2- сурет.

Жоғарыда келтірілген есептің шешімінің схемалық аналитикалық
әдісін граф – схема түрінде көрсетуге болады , мұнда шамалар -
төбелері , ал сол төбелер арасында функциональды өзара байланыстың бар
екендігін көрсететін түзу кесінділер - доғалары (қырлары) болып
табылады. егер шамалар есептің шартында белгісіз болса , (берілмеген )
, граф – схеманың төбелері тік төртбұрыш және де сол шамалар есеп
текстінде айқын берілген немесе айқын берілмеген түрде көрсетілген
жағдайда асты сызық тік төртбұрыш ретінде берілген.
Синтетикалық әдіс .
Бұл әдісті қолдану кезінде алдымен есептің объектілерінің
шамалары арасындағы аралық тәуелділіктер орнықтырылады , содаң соң олар
мен ізделінді шама арасындағы тәуелділіктер табылады (синтезделеді) .
Есептіің шешуінің мұндай әдісі барысында ізделінді шаманы есептің
шарттарында берілген шамалармен байланыстыратын қажетті формула
табылғанға дейін щамалар арасындағы әртүрлі функ- циональді
тәуелділіктер сыналып көрсетіледі.
Синтетикалық әдіс - шешу жоспарының алғашқы ізделінуі барысын өте
адвокатты түрде көрсетеді , шешіп отырған адамның ойы есептің талабын
қанағаттандыратын жолдарды іздеумен сан – саққа жүгіреді.
Есеп №1. есепті синтетикалық әдіспен шешу басқаща ой қорыту
тізбегімен жүзеге асады.
1. лифт кабинасы бірқалыпты үдеумен қозғалады, сондықтан :

Есептің шарттарында лифт қозғаласының шамалары айқын түрде
көрсетілген - S пен t ( жол мен уақыт ) , формуласы негізінде
үдеудің шамасын анықтауға болады , ол ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.