Дөңес программалау: дөңес және ойыс функциялар, дөңес жиындар мен Лагранж функциясының негіздері


Дөңес программалау
Дөңес программалау - математикалық программалау бөлімі. Мұнда мүмкін облыстарды анықтайтын бүтін функция және функция дөңес болып келеді .
Дөңес жиын-жиын өзіне тиісті екі нүктемен қатар, оларды қосатын кесіндіден тұрады.
Анықтама1: Егер кез келген екі нүкте xl, х2 үшін және
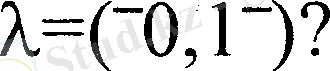
 теңдігі орындалса, онда дөңес жиынында берілген f(xl, . . . , xn) функциясы Дөңес деп аталады.
теңдігі орындалса, онда дөңес жиынында берілген f(xl, . . . , xn) функциясы Дөңес деп аталады.
Анықтама 2: Егер кез келген екі нүкте xl, х2 үшін және кез келген А үшін
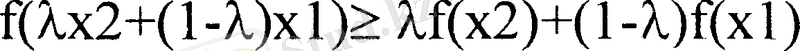 теңсіздігі орындалса, онда дөңес жиынында берілген f(xl, . . . , xn) функциясы ойыс д. а.
теңсіздігі орындалса, онда дөңес жиынында берілген f(xl, . . . , xn) функциясы ойыс д. а.
Анықтама 3: Шарттың жүйелілігі gi(xi) <bi, мұндағы
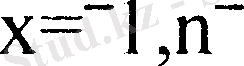 А4: Егер f(xl, . . . , xn) фунцкиясы дөңес (ойыс), ал
А4: Егер f(xl, . . . , xn) фунцкиясы дөңес (ойыс), ал
 функциясы дөңес болса,
Дөңес программалау есебі
деп аталады.
функциясы дөңес болса,
Дөңес программалау есебі
деп аталады.
Анықтама 5: Лагранж функциясы дегеніміз:
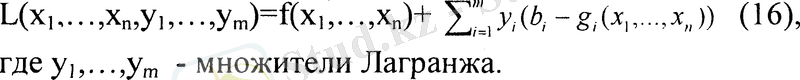
Мақсаттық функциясын ықшамдау мақсатында мүмкін ( x ) оңайлатылған шек қоюлар және мүмкін облысын М -әрімен белгілейміз. Осындай шек қоюлардың бірі Дөңестік шарты деп аталады.
Егер кез келген х 1 и х 2 нүктелері және [х 1 , х 2 ] кесіндісін қосатын барлық нүктелер М көпмүшесіне тиісті болса, М көпмүшесі Евклид кеңістігінде Дөңес деп аталады.
Осы анықтамадан тікелей шығатыны, кез келген дөңес көпмүшелердің қыиылысуының өзі дөңес болып табылады. Бұл қасиеттің қажеттілігі мына шарттарға байланысты. Айта кетеітн болсақ, алдында атып өткендей, мүмкін мәндер облысы әдетте мына теңдік пен теңсіздік арқылы беріледі.
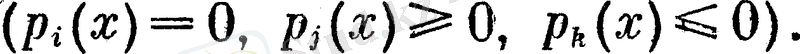 Мұндай жүйе дөңес көпмүшені анықтайтынын білу үшін, берілген әрбір мүшелері тедік пен теңсіздіктермен берілген облыстың дөңес болып келуі. Бұл әдіс сызықтық программалауда да кеңінен қолданылады және
Мұндай жүйе дөңес көпмүшені анықтайтынын білу үшін, берілген әрбір мүшелері тедік пен теңсіздіктермен берілген облыстың дөңес болып келуі. Бұл әдіс сызықтық программалауда да кеңінен қолданылады және
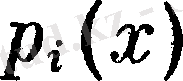 функциясы мынадай түрде болады:
функциясы мынадай түрде болады:
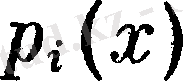
 , х нүктесінің координаталары мен барлық коэфициенттері, яғни
, х нүктесінің координаталары мен барлық коэфициенттері, яғни
 және
және
 тұрақты.
тұрақты.
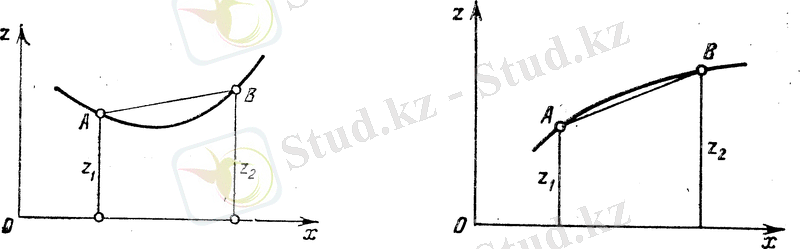
Егер функция М дөңес көпмүшесінде анықталып, және кез келген х 1 және х 2 нүктелерінде күпмүшелері f(x) функциясының кез келген х бөлігіндегі [х 1 , х 2 ] сызықтық функциядағы f(x 1 ) және f (х 2 ) нүктелерінің мәндері артпаса, кез келген М f(x) функциясы дөңес немесе анығырақ айтсақ, төменге қарай дөңес болады
Басқаша айтқанда, егер «үстінде» және «жоғары» сөздерін пайдаланып, ось бойындағы кесінді
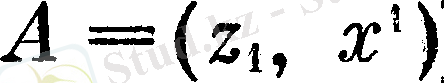 мен
мен
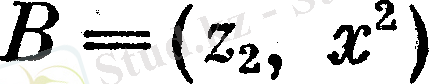 нүктелерін кеңістікте
нүктелерін кеңістікте
 координатасында
координатасында
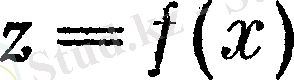 функциясының ең жоғарғы нүктесінде орналасады деп айтуға болады.
функциясының ең жоғарғы нүктесінде орналасады деп айтуға болады.
n=1 шамасы үшін 1-сурет көрсетілген. Жалпы алғанда
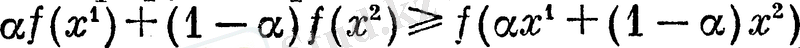 теңсіздігімен
теңсіздігімен
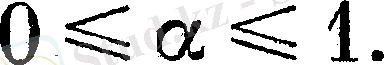 мәндерінде сипатталады.
мәндерінде сипатталады.
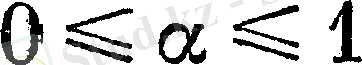 мәнінде
мәнінде
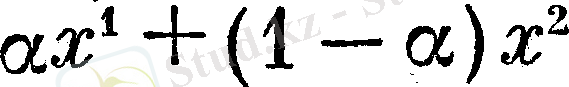 функциясы
функциясы
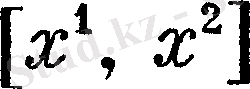 нүктелерінде әр түрлі мәндерге ие болатынын көруге болады. Көрсетілген теңсіздіктен табатынымыз, кез келген сызықтық функция дөңес болып табылады.
нүктелерінде әр түрлі мәндерге ие болатынын көруге болады. Көрсетілген теңсіздіктен табатынымыз, кез келген сызықтық функция дөңес болып табылады.
Егер келтірілген анықтамадағы
 теңсіздігін
теңсіздігін
 теңсіздігіне алмастырсақ, онда ойық функцияның анықтамасын аламыз. Ал бұл дегеніміз, яғни жоғарыға қарай дөңес дегенді білдіреді.
теңсіздігіне алмастырсақ, онда ойық функцияның анықтамасын аламыз. Ал бұл дегеніміз, яғни жоғарыға қарай дөңес дегенді білдіреді.
Қорытындылай келе, айтарым, кез келген сызықтық функция дөңес және сол сияқты ойыс болып табылады.
Шыққан дөңес және ойыс функциялардан олардың үзіліссіз екенін табу оңай. х нүктелерінен тұратын
 дөңес функциясы үшін, мұндағы
дөңес функциясы үшін, мұндағы
 а- тұрақты шама, яғни дөңес көпмүше болып табылады және шектелген көпмүше. Дәл сондай ойыс
а- тұрақты шама, яғни дөңес көпмүше болып табылады және шектелген көпмүше. Дәл сондай ойыс
 функциясы үшін
функциясы үшін
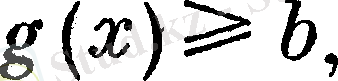 теңсіздігі орындалады, мұндағы b - тұрақты шама. Егер
теңсіздігі орындалады, мұндағы b - тұрақты шама. Егер
 және
және
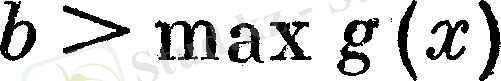 болған жағдайда, бұл көпмүшелер бос болуы мүмкін. Бірақ, бұл көпмүшелер дөңес және ойыс болып қала береді.
болған жағдайда, бұл көпмүшелер бос болуы мүмкін. Бірақ, бұл көпмүшелер дөңес және ойыс болып қала береді.
Алынған облысты деңгейлік облыстар деп атау келісілген, ал олардың шекарасын гипержоғары деңгей (п = 2 тең болса, сызықтар, ал п = 3 төбелер) . Қарастырлып отырған функциялар
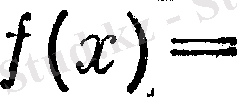
 және
және
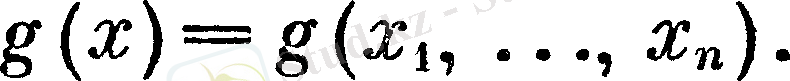
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz