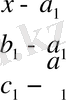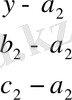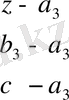Векторлар, түзулер, жазықтықтар және екінші ретті қисықтар мен беттер: глоссарий, теңдеулер және есептер


Глоссарий
Вектор.
- Вектор деп бағытталған кесіндіні атайды.
- вектордың ұзындығы немесе модулі деп оның бас нүктесі мен ұшының ара қашықтығын атайды жәнедеп белгілейді.
- Бір түзудің бойында немесе параллель түзулерде жататынжәневекторлар коллинеар деп аталады жәнетүрінде белгілейді.
- Егер кеңістіктегі үш вектор бір жазықтықта немесе параллель жазықтықтарда жатса, онда оларды компланар деп атайды.
- векторыныңсанына көбейтіндісі деп
- модулі
- векторымен бағыттас, алболсавекторына бағыты қарама-қарсывекторын атайды.
-
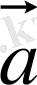 векторының
векторының
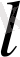 осіндегі проекциясы (пр
осіндегі проекциясы (пр
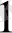
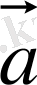 ) деп
) деп

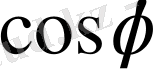 (мұнда
(мұнда
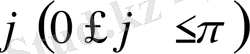 -
-
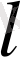
осінің оң бағытымен
вектор бағытының арасындағы бұрыш санын атайды.
-
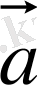 және
және
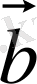 векторларының скаляр көбейтіндісі деп олардың модульдері мен олардың арасындағы бұрыш косинусына көбейтіндісіне тең с санын атайды
векторларының скаляр көбейтіндісі деп олардың модульдері мен олардың арасындағы бұрыш косинусына көбейтіндісіне тең с санын атайды
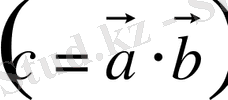 .
.
-
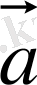 және
және
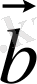 векторларының перпендикулярлық шарты:
векторларының перпендикулярлық шарты:
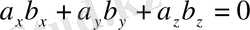 .
.
-
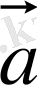 және
және
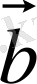 векторларының векторлық көбейтіндісі деп келесі үш шартты қанағаттандыратын
векторларының векторлық көбейтіндісі деп келесі үш шартты қанағаттандыратын
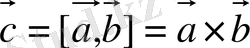 векторларын айтады:
векторларын айтады:
1.
 векторының модулі
векторының модулі
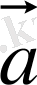 және
және
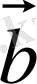 векторларының модульдері мен осы екі вектор арасындағы бұрыш косинусының көбейтіндісіне тең:
векторларының модульдері мен осы екі вектор арасындағы бұрыш косинусының көбейтіндісіне тең:
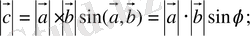
2.
 - әрбір
- әрбір
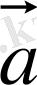 және
және
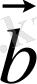 векторларына ортогональ, яғни ол
векторларына ортогональ, яғни ол
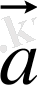 және
және
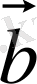 арқылы өтетін жазықтыққа перпендикуляр;
арқылы өтетін жазықтыққа перпендикуляр;
3.
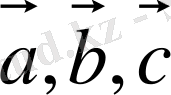 векторларының аралас көбейтіндісі деп
векторларының аралас көбейтіндісі деп
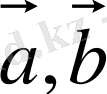 векторларының
векторларының
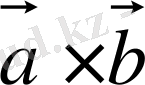 векторлық көбейтіндісі мен
векторлық көбейтіндісі мен
 векторының скаляр көбейтіндісін атайды.
векторының скаляр көбейтіндісін атайды.
Жазықтықтағы түзу.
-
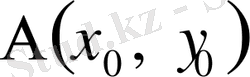 нүкте арқылы өтетін және
нүкте арқылы өтетін және
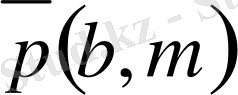 бағыттаушы векторымен анықталатын түзуінің теңдеуі:
бағыттаушы векторымен анықталатын түзуінің теңдеуі:
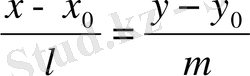
-
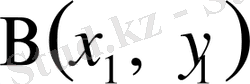 және
және
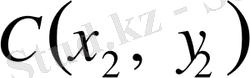 нүктелер арқылы өтетін түзудің теңдеуі:
нүктелер арқылы өтетін түзудің теңдеуі:
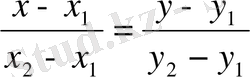 немесе
немесе
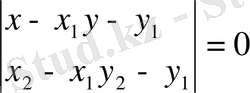
- Түзудің парамеррлік теңдеуі:
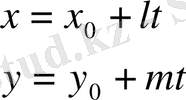
- Түзудің жалпы теңдеуі: Ax+By+C=0
- Түзудіңнориальдық теңдеуі:
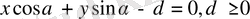
-
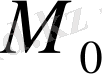 нүктесінен
нүктесінен
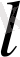 түзуіне дейінгі
түзуіне дейінгі
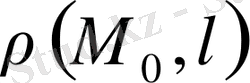 ара қашықтық:
ара қашықтық:
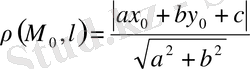
- Түзулердің перпендикулярлық шарты:
- Түзулердің параллельдік шарты:
Жазықтық.
- Жазықтықтың жалпы теңдеуі:
- Жазықтықтың параметрлік теңдеуі:
- Бір түзудің бойында жатпайтын үш нүкте арқылы өтетін жазықтықтың теңдеуі
- Нүкте және нормаль вектормен берілген жазықтықтың теңдеуі:
- Жазықтықтың жалпы теңдеуі:
- Жазықтықтардың арасындағы бұрыш:-
егер
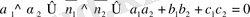
егер
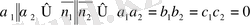
Кеңістіктегі түзу.
- Түзудің канондық теңдеуі:
- Түзудің параметрлік теңдеуі:- (t - параметр)
- Түзулердің арасындағы бұрыш:
Егер
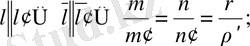
Егер
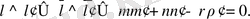
- түзу мен жазықтықтың арасындағы бұрыш:
Егер:а)
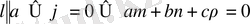
б)
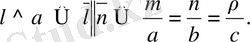
Екінші ретті алгебралық сызықтар.
- Дөңгелек конусты оның төбесіне өтпейтін жазықтықпен қиғанда пайда болған қисықты конустық қима деп атайды.
Екінші ретті алгебралық сызықтар.
- Дөңгелек конусты оның төбесіне өтпейтін жапайда болған қисықтыконустық қимадеп атайды.
- Эллипстің канондық теңдеуі:
- Гиперболаның канондық теңдеуі:
Екінші ретті алгебралық беттер.
- Екінші ретті бет
(алгебралық бет) деп аффиндік координаттар жүйесінде координаттары екінші ретті алгебралық теңдеуді

(мұнда
 - нақты сандар,
- нақты сандар,
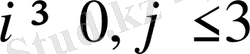 ) қанағаттандыратын кеңістіктегі нүктелер жиыны.
) қанағаттандыратын кеңістіктегі нүктелер жиыны.
- Егер беттегі әрбір М нүктесімен бірге М нүкте арқылы өтетін және берілген
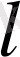 түзуге параллель болатын түзу осы бетте жататын болса, онда мұндай бет
цилиндрлік бет
деп аталады.
түзуге параллель болатын түзу осы бетте жататын болса, онда мұндай бет
цилиндрлік бет
деп аталады.
- Үш осьті эллипсоид:
- Бір қуысты гиперболоид:
- Екі қуысты гиперболоид:
- Эллипстік параболоид:
- Гиперболалық параболоид:.
1.
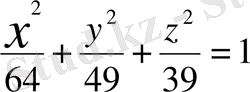
 эллипсоидының бас қималарын, бас осьтерін және төбелерін табыңыз.
эллипсоидының бас қималарын, бас осьтерін және төбелерін табыңыз.
(Жауабы: Оху:
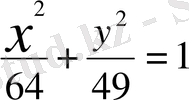 ) .
) .
2. М (2, 0, 1) нүктесінен өтетін және Оху жазықтығын
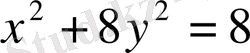 эллипсінің бойымен қиятын эллыипсоидтың канондық теңдеуін табыңыз. (Жауабы:
эллипсінің бойымен қиятын эллыипсоидтың канондық теңдеуін табыңыз. (Жауабы:
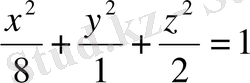 ) .
) .
3.
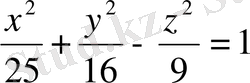 бір қуысты гиперболоидтың жорамал осьтерін, координаталар жазықтықтарындағы қималарын, төбелерін, нақты және жорамал жарты осьтерін табыңыз. (Жауабы: Oz-жорамал осі,
бір қуысты гиперболоидтың жорамал осьтерін, координаталар жазықтықтарындағы қималарын, төбелерін, нақты және жорамал жарты осьтерін табыңыз. (Жауабы: Oz-жорамал осі,
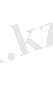
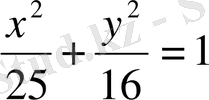 Oxy жазықтығымен қимасы,
Oxy жазықтығымен қимасы,
 (-5, 0, 0),
(-5, 0, 0),
 (5, 0, 0),
(5, 0, 0),
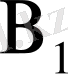 (0, -4, 0),
(0, -4, 0),
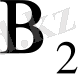 (0, 4, 0) - төбелері;
a
=5, b=4) .
(0, 4, 0) - төбелері;
a
=5, b=4) .
4.
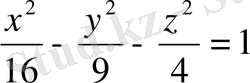 екі қуысты гиперболоидтың бас қималарын, нақты және жорамал жарты осьтерін табыңыз. (Жауабы: Oxy:
екі қуысты гиперболоидтың бас қималарын, нақты және жорамал жарты осьтерін табыңыз. (Жауабы: Oxy:
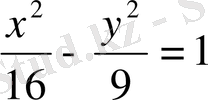 ; Oxz&
; Oxz&
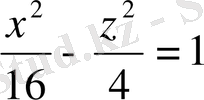 a
=4 - нақты жарты осі; b=3, c=2 - жорамал жарты остері) .
a
=4 - нақты жарты осі; b=3, c=2 - жорамал жарты остері) .
Төменде берілген беттердің түрлерін анықтап сызбасын салып көрсетіңіз:
5.
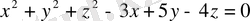
6.
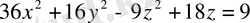
7.
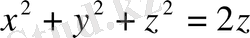
8.
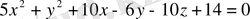
9.
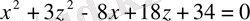
Төменде көрсетілген беттермен шектелген денелерді салыңыз:
10
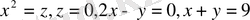
11.
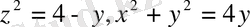
12
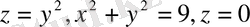
13 .
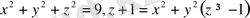
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz