Жиынның элементтері

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 7 бет
Таңдаулыға:

Жиын ұғымы математикада негізгі (анықтауға болматын, бастапқы) ұғым болып саналады. Сондықтан оны тек мысалдармен ғана түсіндіруге болады. Мысалы қайсыбір класс оқушыларының жиын туралы, әлемдегі планеталар жиыны туралы, осы беттегі жиын туралы, орыс алфавитіндегі дауыс дыбыстар жиыны туралы айтуға болады. «Жиын» сөзі математикада «жиынтық», «класс», «жинақ», «коллекция»деген сөздердің, яғни қайсыбір нәрселер жиынтығын сиппатттайтын сөздердің орнына қолданылады, оныңүстіне қарастырылып отырған жиынтықта бір ғана нәрсе болуы немесе бірде бір нәрсе болмауы мүмкін.

Жиын құратын кез келген нәрселер (адамдар, үйлер, кітаптар, елдер, геометриялық фигуралар, сандар т. б. ) оның элементтері деп аталады. Мысалы, дүйсенбі- апта күндері жиынының элементі, 3 саны бір таңбалы натурал сандар жиынының элементі. Жиын мен оның элементтерінің арасындағы «элементі болады» деген байланысты «тиісті» сөзінің көмегі мен де білдіруге болады. Мысалы, 3 саны бір таңбалы натурал сандар жиынына тиісті деп те атауға болады.

Соңғы сөйлемді символдың көмегімен қысқаша жазүға болады: . Бұл жазуда А әрпі арқылы бір таңбалы натурал сандар жиыны белгіленген (жиынды латын алфавитінің бас әріптерімен белгілейді), ал белгісі «тиісті» сөзін алмастырады.

Жалпы жазуы «а нәрсесі А жиынының элементі» немесе «а нәрсесі А жиынына тиісті» деп оқылады. 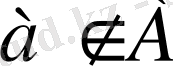жазуын «а нәрсесі А жиынына тиісті емес» немесе«а нәрсесі А жиынының элементі емес» деп оқуға болады.

Жиын элементінің саны шектеулі де, шектеусіз де болуы мүмкін. Мысалы, қайсыбір педучилищеде оқушыларының жиынының элементтерінің саны шектеулі, ал түзудегі нүктелер жиыны шектеусіз.

Жиын тек ьір ғана элементтен тұруы мүмкін. Мысалы, «сан» деген сөздегі дауысты дыбыстар жиыны тек қана бір элементтен- «а» әрпінен тұрады.

Жиын элементінің өздері де жиын болуы мүмкін. Мысалы, мектептегі класстардың жиыны турады айтуға болады.

Нәрсенің қайсыбір жиынға тиісті болу немесе болмау мәселесі білімнің кез келген саласынан жиі кездеседі. Мысалы, оқушы Новиков - комсомол мүшесі дегеніміз оқушы Новиков барлық комсомолдар жиынына тиісті деген тұжырымды білдіреді. Орыс тілінде қайсыбір сөз табына жататындығын анықтау мәселесі қарастырылады.

Жиын ұғымы және онымен байланысты басқұа ұғымдар математиканы алғаш оқудың негізі болады және онда кеңінен пайдаланылады. Кейбір оқулықтарда «жиын» термині кездеспейді, бірақ бұл ұғым айқындалмаған түрде пайдаланылады, ал бірқатар эксперимент кітаптарда жиын ұғымы символикасымен қоса айқын түрде пайдаланылады. Сан, натурал сандарды қосу және көбейту амалдары және олардың қасиеттері, геометриялық фигура сияқты маңызды ұғымдардың қалыптасуы мектептегі математика курсында теориялық - жиындық негізінде жүзеге асады.

2. егер әрбір нәрсе туралы оның жиынға тиісті немесе тиісті емес екендігін айта алатын болсақ, онда жиын берілген деп саналады.

Жиынды оның барлық элементтерін атау арқылы анықтап беруге болады. Егер де a, b, c, d - әр түрлі нәрселердің белгіленулері болса, онда осы нәрселердің жиынын

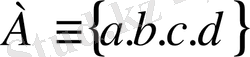
Түрінде жазып оны «а жиыны a, b, c, d элементтерінен тұрады» деп оқиды.

Жиынның берілуінің тағы бір тәсілі оны құрайтын нәселердің ортақ қасиетін атау болып табылады. Мұндай қасиетті сипаттамалық қасиет деп атайды. Элементтердің сипаттамалық қасиеті көрсетілген жиынды былай жазуға болады: фигуралық жақшалар ішіне алдымен элементтерінің белгіленуін жазады. Содан кейін вертикаль сызықша қояды да сызықшадан соң осы жиын элементтеріне және тек соларға ғана тән қасиетті жазады. Мысалы 7-ден кіші натурал сандар жиыны а былайша жазылады:

А= {x/x-натурал сан, x<7}

Сонымен қандайда бір жиын берілген болуы үшін не оның элементтерін атап шығу, не оның элементтеріне тән қасиетті көрсенту керек. Екінші тәсіл біріншіге қарағанда жалпылау екенін айта көрсетеміз. Мәселе мынада: жиынның элементтерін атап шығу осы жиын шектеулі болғанда ғана мүмкін, ал жиын элементтерінің ортақ қасиетін жиын шектеулі болса да, шектеусіз болса да көрсетуге болады.

Бірақ кейбір кезде шектеусіз жиынды да бірінші тәсілді пайдаланып жазып көрсетуге болады. Мысалы, барлық натурал сандар жиынын N әрпі арқылы белгілеп мына түрде

N={1, 2, 3, 4…}жвзуға болады.

Әрине жиынды тек көп нүктелер орнында не боладтыны белгілі жағдайда ғана осы түрде жазуға болады.

Барлық натурал сандардан және нольден тұратын жиынды N ₀ арқылы белгілеп былай жазады: N ₀ = {0, 1, 2, 3, 4, …} бұл жиынды оң бүтін сандар жиыны деп атайды.

3. Әр түрлі жиындардың арасында бірде бір элементі жоқ жиындарды да кездестіруге болады. Мысалы, сіздің топтағы тенниспен айналысатын оқушылардың тізімін немесе, қысқаша айтқанда, сіздің топтағы теннисші - оқушылардың Т жиынын құру керек делік. Бірақ топта ондай оқушы жоқ болып шықты. Ендеше Т жиынында бірде бі элемент жоқ.

Бірде бір элемент жоқ жиынды бос жиын деп атайды. Және оны Øбелгісімен белгілейді.

Бос жиынмен теңдеулерді шешуде де кездеседі.

4. Егер А женә В екі жиын бірдей элементтерден тұратын болса, онда оларды тең жиындар деп атайды және А=В түрінде жазылады. Мысалы, A={3, 5, 7, 9} және B={7, 3, 9, 5} жиындары өзара тең, өйткені бірдей элеметтерден тұрады. Элементтерінің орындарын ауыстырғаннан жиын өзгермейді.

Жиындардың тең болу ұғымы мына жағдаймен байланысты: бір ғана жиын мүлдем әр түрлі сиппатамалық қасиеттер көмегімен берілуі мүмкін. Мысалы, A={1, 2, 3, 4, 5}жиынын 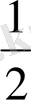және 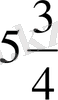сандарының аралығындағы натурал сандар жиыны немесе x<6 теңсіздігінің натурал шешімдерінің жиыны деп те қарастыруға болады.

5. Айталық, А сіздің педучилищедегі барлық оқушылар жиыны, ал В сіздің группадағы оқушылар жиыны болсын. әрине В жиыны А жиынының бір бөлігі, немесе, басқаша айтқанда, В жиыны А жиынына кіреді. Мұндай жағдайда В жиыны А жиынының ішкі жиыны деп аталады, оны (немесе ) түрінде жазып, «В жиыны А жиынының ішкі жиыны» деп оқиды. белгісі жиындар арасындағы «ішкі жиыны болады» деген мағынадағы байланыстылықты көрсетеді.

А жиынының бос емес В ішкі жиыны А жиынымен дәлме-дәл келмейтін болса, онад оны меншікті ішкі жиын деп атайды. А жиынының А және Ø ішкі жиындарын оның меншікті емес ішкі жиындары деп атайды.

Мысалы, A={2, 4, 8} жиынының алты меншікті ішкі жиыны бар. {2}, {4}, {8}, {2, 4}, {2, 8}, {4, 8}; екі меншік емес ішкі жиыны бар: {2, 4, 8} және Ø.

Жиын және ішкі жиын ұғымдарын меңгерген соң, біз енді кейбір геометриялық ұғымдарды дәлірек анықтауымызға болады. Геометриядағы ең маңызды ұғым- геометриялық фигура ұғымы «нүкте» және «жиын» ұғымдары арқылы анықталады. Геометриялық фигура деп нүктелердің кез келген бос емес жиынын айтады. Олай болса, жеке алынған нүкте де және нүктелердің шектеулі жиыны да геометриялық фигура болып табылады. Кесінді, сәуле, түзу, шар т. с. с. нүктелердің шектеусіз жиындары геометриялық фигуралар болып табылады.

6. А- қайсыбір мектептің комсомолдарының жиыны, В- осы мектептегі қыз балалар жиыны, ал С- мектептің спортсмендерінің жиыны болсын. Осы аталған жиындардың барлығын мектептің барлық оқушыларының жиынының ішкі жиындары деп қарастыруға болады. Барлық жиындары бір ғана I жиынның ішкі жиындары ретінде қарастыратын жағдай аз кездеспейді. Осындай I жиынын универсал жиын деп атайды. Ендеше, егер I - мектептің барлық оқушыларының жиыны болса, онда 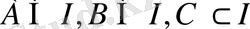болады. Универсал I жиынын тік төрт бұрыш түрінде, ал оның ішкі жиындарын - осы тік төрт бұрыштың ішіндегі дөңгелектер түрінде кескіндеуді келісейік. Онда біздің қарастырып отырған I, А, В, С жиындарын графмкалық түрінде мынадай етіп кескіндеуге болады.

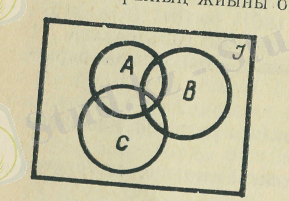
7. Екі жиынның элементтерінен жаңа жиындар құруға болады. A={0, 2, 4, 6, 8} және B={-2, -1, 0, 1, 2} екі жиын берілген болсын. Элементтері берілген А және В жиындарының екеуіне де тиісті жаңа С жиынын құрайық: C={0, 2}. Осылай құрылған С жиынын А және В жиындарынң қиылысуы деп атайды. Сонымен:

А және В жиындарының қиылысуы деп А және В жиындарының екеуіне де енетін элементтерден және тек қана сол элементтерден тұратан жиынды айтады. А және В жиындарының қиылысуын өрнегімен белгілейді, мұндағы - жиындарының қиылысуы белгісі.

Жиындардың қиылысуының мынадай бірнеше қасиеттері бар:

Кез келген А және В екі жиын үшін коммутативтік (орын ауыстырымдылық) заң орындалады: шынында да, жәнежиындары А жәнеВ жиындарына ортақ элементтерден тұрады, олай болса, =.
Кез келген А, В және С жиындары үшін ассоциативтік (терімділік) заң орындалады:
Егер, ондаболады.
Кез келген А жиыны үшінжәнеболады.

8. Берілген екі жиыннан жаңа жиын құрудың тағы бір тәсілін қарастырайық.

А және В жиындарының бірігуі деп не А не В жиындарының ең болмағанда біреуіне енетін элементтерден тұратын жиынды айтады.

А және В жиындарының бірігуін деп белгілейді, мұндағы жиындарының бірігуінің белгісі. Мысалы, A={1, 3, 5} және B={2, 4, 6, 8} жиындарының бірігуі ={1, 2, 3, 4, 5, 6, 7, 8} жиыны болады.

Жиындардың бірігуі амалының бірқатар қасиеттері бар.

Кез келген А және В жиындары үшін коммунативтік заң орындалады:=.
Кез келген А, В және С жиындары үшін ассоциативтік заң орындалады:. Бұл заң үш және оннан да көп жиындардың бірігуін табуға мүмкіндік береді.
Егер, ондаболады.
Кез келген А жиыны үшінтеңдіктері орындалады.
Кез келген А, В және С жиындары үшін қиылысудың бірігуге қатысты дистрибутивтік (үлестірімдік) заңы орындалады:

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.