Кванттық статистиканың негіздері: фазалық кеңістік, Гиббстің канондық үлестірімі және Бозе-Эйнштейн мен Ферми-Дирак статистикалары

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 3 бет
Таңдаулыға:

Жоспар:

І. Кіріспе

ІІ. Негізгі бөлім Кванттық стстистиканың негізі

а) Фазалық кеңістік

б) Бозе - Эйнштейн және Ферми - Дирактың кванттық статистикалары

ІІІ. Қорытынды

Қолданылған әдебиеттер

Егер классикалық статистикада ұқсас бөлшектердің бір тобының екінші тобынан ажыратылатындығы айтылса, кванттық статистикада керісінше ұқсас бөлшектердің ажыратылмаушылық принципін түсіндірдік. Оның үстіне спиндік сандарының бүтін және жартылай болуының себептерінен бөлшектер әр түрлі статистикалық заңдылықтарға бағынатын болады.

Айталық, берілген n бөлшектерден түзілсін. Сонда жүйедегі бөлшектердің барлық импульстері мен көпөлшемді кеңістік берілсін. Кеңістіктің әрбір нүктесіне 6n саны сәйкес келеді, себебі әрбір бөлшектің күйін 3 координатамен ( x, y, z ) және осы координаттарға сәйкес импульстің 3 проекциясын 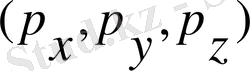анықтайды. Сонымен осы кеңістіктегі өзара перпендикуляр координаттық осьтер саны 6n-ге тең. Сондықтан осындай 6n өлшемді кеңістік фазалық кеңістік деп аталады. Сөйтіп, жүйедегі әрбір микробөлшектің күйін осы 6n өлшемді фазалық кеңістік анықтайды, өйткені осы бөлшекке сәйкес жүйедегі барлық бөлшектердің координаттары мен импульстері осындай болады.

Енді 6n өлшемді фазалық кеңістікті кішігірім элементар ұяшықтарға бөлейік, сонда барлық бөлшектердің координаттарының жинағы - q, ал олардың импульстерінің проекцияларының жинағы - p болсын.

Сонымен зат бөлшектерінің корпускулалық және толқындық қасиеті және Гейзенбергтің анықталмаушылық қатыстары осы элементар ұяшықтардың көлемі Планк тұрақтысы h ³ - тен кем болмайтынын көрсетеді. Әдетте осы элементар ұяшықтарды фазалық көлем деп атайды.

Егер де жүйедегі бөлшектің координаттары мен импульстерін ескермей, тек қана квантталған энергиясы белгілі болса, онда жүйенің күйін үздіксіз емес, дискретті функцияның үлестірілуі арқылы сипаттауға болады.

Осындай функцияның үлестірілуі туралы өте маңызды өрнектің жалпы түрін американ физигі Д. Гиббс ( 1839 - 1903 ) тапты. Бұл тұжырым Гиббстің канондық үллестірілуі деп атайды.

Кванттық статистикадағы Гиббстің канондық үлестірілуінің түрі мынадай:

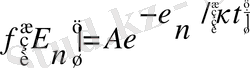(45)

мұндағы А - тұрақты шама, n - барлық кванттық сандардың жиыны, ол жүйенің күйін сипаттайды.

Сонда белгілі бір жүйенің ықтималдық тығыздығы деп функцияның үлестірілуін айтуға болады. Олай болса жүйенің ықтималдық тығыздығы мынаған тең

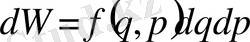
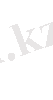(46)

Сөйтіп, 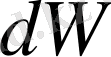жүйе күйінің координаттары мен импульстерінің 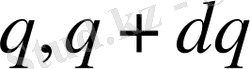және 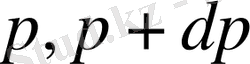аралықтарында болатын ықтималдығын көрсетеді.

Бозе - Эйнштейн және Ферми - Дирактың

кванттық статистикалары

Біз бұдан бұрын классикалық статистикада қарастырылған идеал газдарды енді кванттық статистикада тұрғысынан зерттейік. Ондай идеал газ молекулалар мен атомдардан түзіледі дедік. Олай болса, кванттық жүйеде ұқсас бөлшектердің жиынтығы осы күйді сипаттайтын толтыру саны (N) деп аталатын сандардан түзіледі. Осы сандар кванттық күйдің толтыру көрсеткішін сипаттайды. Егер бөлшекті жүйесі спиндік саны ноль немесе бүтін сандарға тең болатын бозон бөлшектерден түзілсе, онда толтыру сандары кез келген бүтін сандарды қабылдайды, яғни ( 0, 1, 2, 3, . . . )

Ал бөлшектер жүйесі спиндік саны жартылай сандарға тең болатын фермион бөлшектерінен түзілсе, онда толтыру сандары тек екі мәнді ғана қабылдайды, яғни бос күйлер үшін 0 мәнді де толтырылған күйлер үшін бір мәнді болады

Сонымен барлық толтыру сандары жүйедегі бөлшектер санына тең болуы керек. Сөйтіп берілген кванттық күйдегі бөлшектердің орташа саны кванттық статистика көмегімен есептеуге болады.

Ендеше идеал газдағы бозон бөлшектерінің орташа саны Бозе - Эйнштейннің кванттық статистикасы бойынша есептеуге болады, Д. Бозе (1858 - 1937) үнді физигі. Сонда бозондардың энергиясы бойынша үлестірілуі Гиббстің канондық үлестірілуіне негізделген. Сөйтіп Бозе - Эйнштейннің кванттық статистикасы бойынша бөлшектердің орташа толтырылу саны мына өрнек бойынша есептеледі

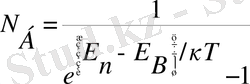(47)

мұндағы 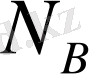- энергиясы 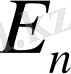- кванттық күйдегі бозондардың орташа саны, Т - термодинамикалық температура, к - Больцман тұрақтысы, 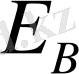- энергияның нормалану тұрақтысы.