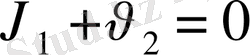Орындалу нәтижесінде және ойыншылар ұтысы

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:

Қазақстан Республикасынң Білім және ғылым министрлігі

Ы. Алтынсарин атындағы Арқалық мемлекеттік

педагогикалы институты

Жаратылыстану және ақпараттандыру факультеті

Тақырыбы: Аралас стратегиядағы матрицалық ойындар шешімін сызықтық программа есебінде құру.

Орындаған: И - 31 тобының студенті

Абдибаева Г.

Тексерген: УтельбаеваА.

Арқалық, 2009ж

Матирицалық ойындар және сызықтық

бағдарламалаудың міндеттері.

Екі қатысушының қарама - қарсы қалаулары қақтығысатын жағдайды қарастырайық.

Бірінші және екінші әріптестің қалауларының сандық қасиетін 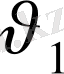және 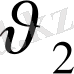деп белгілейік. (Сәйкесінше 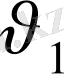- бірінші ойынның ұтысы, 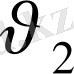- екінщі ойыншы жеңісі) .

Анықтама. 8. 1. Орындалу нәтижесінд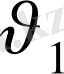е және 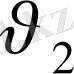ойыншылар ұтысы 0 - ге тең.

ережелер ара қатынасы нөлдік салмағы матрицалық ойын деп аталады, және А әрпімен белгіленеді.

Анықтама 8. 2. 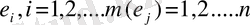таза стратегиясы дегеніміз бірініші (екінші) ойыншының мүмкін болатын жүрісінің арақатынасы.

Бірінші ойыншының 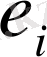таза стратегиясын (екінші ойыншының 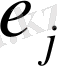таза стратегиясын) 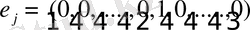. т дәрежелі бірлік векторы ретінде 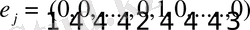п дәрежелі бірлік векторы ретінде елестетелік.

Анықтама 8. 3. Бірінші ойыншының i нөмерлі таза стратегияны таңдау, ал оның қарсыласының j нөмерлі таза стратегияны таңдау шартымен a _ij бөлшегі бірінші ойыншының ұтыс көлеміне (екінші ойыншының жеңіліс көлеміне) тең болатын 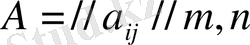матрицасы А ойыны ұтыстарының матрицасы немесе төлемдік матрица деп аталады.

Анықтама 8. 4. Бірінші ойыншының 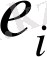таза стратегиясын таңдау мүмкіндігін (екінші ойыншының 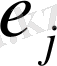таза стратегиясын таңдау мүмкіндігін) и _і

Құрамдық бөлшегін білдіретін 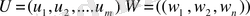векторы бірінші ойыншының аралас стратегиясы деп аталады.

екені анық. (1. 1. )

Анықтама 8. 5. Мәні бірінші ойыншының әріптестерімен аралас стратегиясын 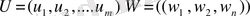таңдаудағы ұтысты математикалық күтуіне тең болатын

(1. 2. )

функциясы А ойынның төлемдік функциясы деп аталады.

Анықтама 8. 6. Егер 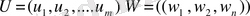қатынасы орындалатын болса, онда 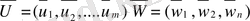стратегияларға оптимальды деп аталады.

Теорема. Әрбір нөлдік салмағы А матрицалық ойынының стратегияларда шешімі бар, яғни қатынастарды қанағаттандыратын 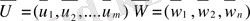оптималды стратегиялары бар.

Сызықтық бағдарламалаудың екі түзудің жұбы мен А= //a _ij // m, n матрицалық ұтысы бар А ойынын қарастырайық. Мұндағы

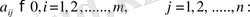
бастапқы мәселе

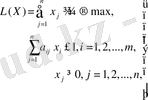(1. 3. )

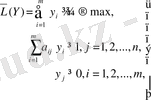(1. 4. )

Теорема. 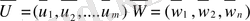оптимальды стратегиялары (1. 3. ) және (1. 4. ) есептердің оптималдьды жоспарлары мен

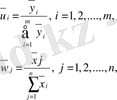(1. 5. ) (1. 6. )

формулалармен тығыз байланысты.

Сонымен қатар А ойынының құны тең

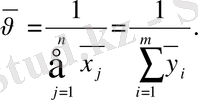(1. 7. )

Енді сызықтық бағдарламалаудың туынды екі бетті есептер жұбын қарастырайық: бастапқы мәселе

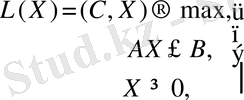(1. 8. )

және екі бетті есеп

(1. 9. )

(1. 10. )

матрицасын түземіз.

(мұндағы А’ A, B және C’ - баған векторлары мен B’ және С - қатар векторларына транспонирленген матрица) .

Анықтама 8. 7. Егер 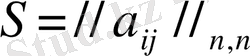ұтыстар матрицасы қиға сисмметриялы болса, яғни 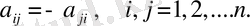болса, онда S ойыны симметриялы деп аталады.

Теорема. Сызықтық бағдарламалаудың екі бетті есептер жұбының (1. 8), (1. 9. ) . 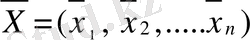және 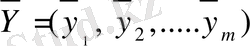шешіміне тек қана (1. 10. ) ұтыстар матрицасы бар S симметриясы болғанда ие болады. Сонымен қатар

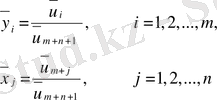(1. 11. ) (1. 12. )

Сызықтық бағдарламалау мәселесіне

матрицалық ойынды келтіру.

А матрицасы m x n өлшеміне ие ойынды қарастыралық:

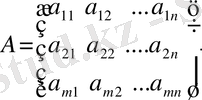Матрицаның ерлі нүктесі болмағандықтан, ойын шешімі аралас стратегияда көрсетілген: 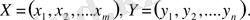А ойыншының оптимальды стратегиясы барысында шартты орындалады, ал В ойыншының оптимальды стратегиясы шартын қанағаттандырады. Осылайша келесі шектеулер орын алатын А ойыншының оптимальды стратегиясын табу мәселесін қарасытруға болады.

(1. 1. )

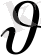(ойын құны) көлемі белгісіз, дегенмен деп есептеуге болады. Егер матрица элементтері теріс болмаса, соңғы шарт әрқашан орындалады. Бұған матрицаның әрбір элементіне әлдебір оң санды қосу арқылы қол жеткізуге болады.

Теңсіздіктердің барлық мүшелерін 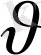бөлу арқылы шектеу жүйесін жасайық. Нәтижесінде

аламыз. (1. 2. )

Мұнда

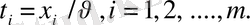
шартынан 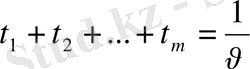туындайды.

Ойын шешімі 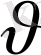мәнін максималдауытиіс, яғни 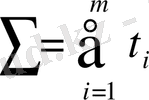функциясы максимальды мәнге ие болуы тиіс. Осылайша сызықтық бағдарламалау есебі алынады: (1. 1. ) шектеуімен 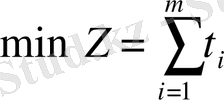және 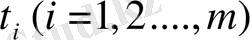ауыспалының теріс болмауы сияқты қосымша шарттар арқылы.

Оны шешу арқылы t _i мәнін және 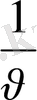көлемін табамыз, сонан соң 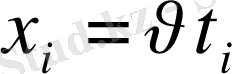мәнін табамыз.

В ойыншының стратениясын анықтау үшін келесі шарттарды жазайық.

(1. 3. )

Теңсіздіктердің барлық мүшелерін 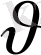- ға бөліп,

аламыз (1. 4. )

Мұнда, 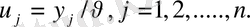u ₁ , u ₂ , …., u _n ауыспалары (1. 4. ) шарттары орындалатындай және 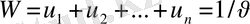функциясының максимумына жететіндей болып таңдалуы керек.

Осылайша, ойынды шешуге керекті сызықты бағдарламалаудың екі бетті симметриялы есептер жұбын аламыз. Симметриялық қасиетті пайдалана отырып, аз есептеуді талап ететін бірін орындауға болады, ал екінші есеп шешімін екі беттілік оптимальды жоспар негізімен шешуге болады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.