Үшінші ретті анықтауыштар

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 10 бет
Таңдаулыға:

АНЫҚТАУЫШТАР

п- ші ретті квадраттық матрица

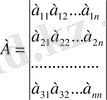
алалық. Бұл матрицаның элементтерінен әрбір жолдан бір және әрбір бағаннан бір ғана элемент болатындай барлық мүмкін көбейтінділерді құралық. Әрбір көбейтіндідегі көбейткіштер саны п , сондықтан оларды бірінші индекстері (1, 2, . . . , п ) ауыстыруын сақтап орналастыруға болады. Сонда көбейтінді

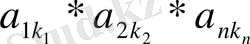(1)

түрінде жазылады, k ₁ , k ₂ , k ₃ , дегеніміз 1, 2, 3, . . . , п сандарының кейбір

ауыстырулары.

Егер инверсия саны жұп болса (1) көбейтіндісінін алдына оң таңба, ал

инверсия тақ болса теріс таңба қоюға келісеміз.

Барлық (1) түріндегі көбейткіштерді таңбаларды ескере отырып қосып А матрицасының анықтауышы немесе детерминанты деген санды аламыз. Анықтауышты

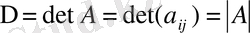
символдарының бірімен белгілейді.

Анықтаушы нольге тең емес квадраттық матрицаны өзгеше емес, ал анықтауышы нольге тең болса өзгеше матрица деп атайды.

Екінші ретті анықтауыштар.

Анықтама. 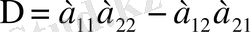санын екінші ретті анықтауыш деп атайды да, оны былай белгілейді

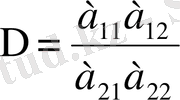(1`)

Сонда анықтама бойынша

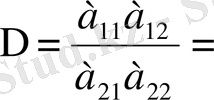
(2)

Ал 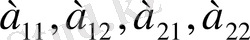сандарын анықтауыш элементтері деп атайды. (1) анықтауышта 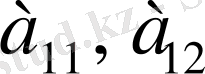элементтерін оның бірінші жолы, 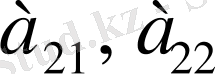- екінші жолы, ал 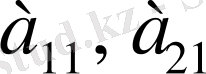элементтерін - бірінші бағаны, 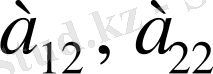- екінші бағаны деп айырып айтады.

Екінші ретті анықтауыштың жолдары не бағандары элементтері пропорционал болғанда, тек сонда ғана ол нольге тең болады; мұны тексеру қиын емес. Шынында да, (2) ескеріп, былай жазамыз

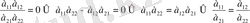немесе 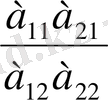(3)

Ескерту. Бөлшектердің бөлімдері ноль болғанда (3) пропорциялар мағынасын жояды; алайда символ түріндегі осы жазуды пайдалану қолайлы: егер бөлімнің бірі нольге тең болса, онда сәйкес алымды нольге теңестіреді де, пропорцияның өзін 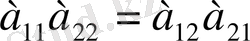теңдігінің орындалуы деп түсінеді.

Үшінші ретті анықтауыштар.

1-анықтама. Үшінші ретті анықтауыш деп мына санды айтады да, оны былай белгілейді

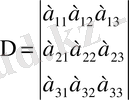. (10)

Сонда анықтама бойынша

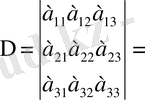
(11)

Үшінші ретті (10) анықтауыш бірінші, екінші, үшінші жолдардан және де бірінші, екінші үшінші бағандардан тұрады; а ( i =1, 2, 3; j =1, 2, 3) сандары анықтауыштың элементтері дей аталады. Мұнда бірінші индексі осы элемент тұрған жолдың i нөмірін көрсетсе, екінші индекс j - баған нөмірін көрсетеді. Сондай-ақ а элементі i - нші жол мен j -інші бағанның қиылысқан жерінде орналасқан деп те айтылады.

элементтері орналасқан диагональ (10) анықтауыштың бас диагоналы деп, ал элементтерінен құралған диагональ қосымша диагональ деп аталады.

Үшінші ретті анықтауыш (11) формула бойынша 3!=6 қосылғыштардың қосындысы болып табылады. Әрбір қосылғыш анықтауыштың мүшесі делінеді. Анықтауыштың әрбір мүшееі әр басқа жолда және әр басқа бағанда орналасқан (әр жол мен әр бағаннан бір-бірден ғана алынған) үш элементтің көбейтіндісі болып табылады және бұл көбейтінді анықтауышқа не плюс, не минус таңбасымен енеді.

Үшінші ретті анықтауыштың мүшелерін (таңбасымен қоса) қарапайым құру ережесін көрсете кетейік. Бірінші мүше деген - анықтауыштың бас диагоналында тұрған элементтердің көбейтіндісі. Екінші және үшінші мүшелер- бас диагональға параллельдер бойында орналасқан екі элемент пен анықтауыштың қарсы бұрышында тұрған элементтің көбейтінділері. Бұл үш мүше плюс таңбасымен алынады. Минус таңбасымен алынатын мүшелер де осыған ұқсас түрде құрылады. Мұнда бас диагональдың орнына қосымша диагональ қарастырылады. Осы айтылғандарды схема түрінде былай көрсетуге болады

Бұл ереже үшбұрыш ережесі деп аталады.

Бұдан да оңай мынадай ереже бар. Анықтауыш құралатын таблицаға он, жағынан тағы бір рет бірінші, одан соң екінші бағандарды тіркеп жазады. Осы шыққан жаңа таблицада плюс таңбасымен алынатын мүшелерді құрайтын элементтерді тұтас сызықпен, ал минус таңбалы мүшелерді құрайтын элементтерді, пунктир сызықпен қосады. Схема түрінде:

Мысал. Үшбұрыш ережесі бойынша мына анықтау-ышты есептеу керек.

1 4 -2

3 7 1

4 -1 6

1 4 -2

3 7 1 =1*7*6+4*1*4+3*(-1) *(-2) - (-2) *7*4-3*4*6 - 1*(-1) *1=42+16+6+56-4 -1 6 72+1=49.

Енді жоғарыда аталған анықтамаға пара-пар, бірақ кез келген ретті анықтауыш үшін де жарамды, үшінші ретті анықтауыштың анықтамасын келтірейік. Ол үшін анықтауыштың белгілі таңбамен альшған әрбір мүшесі үш элементтің көбейтіндісі (және олар әр жолдан, әр бағаннан бір-бірден ғана алынған) екенін ескереміз. Бұл элементтерді әрбір көбейтіндіде олардың бірінші индекстерінің - олар орналасқан жол нөмірі - өсу ретімен орналастыруға болады; (11) қосындыда дәл осылай алынған да. Осы әлементтердің баған нөмірлері (1, 2, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1), (1, 3, 2), (2, 1, 3) түрінде алынады. Бұлар 1, 2, 3 сандарынан жасалған мүмкін болатын барлық алмастырулар. Алмастырудағы инверсия (немесе ретсіздік) деп үлкен нөмі р-дің кіші нөмірден бұрын келуін айтады. Мысалы, (2, 3, 1) алмастыруында екі инверсия бар: 2 нөмірі 1-ден бүрын және 3 нөмірі 1-ден бұрын түскен. Жоғарыда жазылған алты алмастырудьщ алғащқы үшеуінде инверсиялар саны жұп та, кейінгі үшеуінде - тақ. Бұған қоса ескертеріміз, (. 11) қосындыдағы алраш-қы үш мүше плюс таңбалы да, кейінгі үш мүше минус таңбалы.

Анықтауыштардың қасиеттері. Үшінші ретті анықтауыштардың бірнеше қасиеттерін қарастырайық. Бұл қасиеттер, сызықтық алгебраның толық курсында дәлелденетіндей-ақ, кез келген ретті анықтауыштар үшін де дұрыс болып қала береді.

1) Анықтауыштыц жолдарын бағандармен (және керісінше де бағандарын жолдармен) ауыстырып жазғаннан оның шамасы өзгермейді, ягни

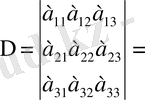
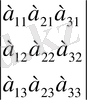(12)

Бұл қасиетті дәлелдеу үшін (12) теңдіктің оң жақ және сол жақ бөлігіндегі анықтауыштарды үшбұрыш ережесі бойынша ашып жазып, олардың бірдей мүшелерден тұратыныңа көз жеткізсе болғаны.

Жоғарыда дәлелденген қасиет бойынша анықтауыштың жолдары мен бағандары тең түседі. Сондықтан ілгеріде анықтауыштың қасиеттерін тек жолдарға қатысты тұжырымдап және дәлелдеп, оларды бағандар үшін де дұрыс деп есептейміз.

2) Егер анықтауыштыц бір жолының барлық элементтері нольге тең болса, ондай анықтауыш нольге тең болады.

Анықтауыштың қайсыбір жолы нольдерден ғана тұрады делік. Анықтауыштың әрбір мүшесі көбейткіш ретінде осы жолдың бір, тек бір ғана элементін қамтиды, сондықтан ол нольге тең. Демек, олардың қосындысы - анықтауыш та нольге тең болады.

3) Егер анықтауыштыц екі жолын ауыстырып қойса, оның таңбасы қарама-қарсы таңбаға әзгереді.

Енді (10) анықтауышта, мысалы, бірінші мен үшінші жолды ауыстырып қояйық. Жаңа шыққан анықтауышты ' деп белгілеп, үшбұрыш ережесі бойынша мынаны табамыз

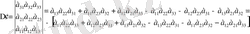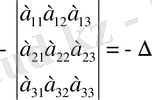
4) Егер анықтауыштың екі жолы бірдей болса, оның шамасы нольге тең болады.

Алынған анықтауыштың шамасын А деп белгілейік. Егер оның бірдей екі жолының орнын ауыстырсақ, 3) қасиет бойынша оның шамасы (- ) -ға тең болады, ал екінші жағынан алғанда, оның шамасы өзгермейді. Сондықтан = - 2 = 0 = 0.

5) Егер бір жолдың барлық элементтерін бір ғана 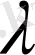санына көбейтсек, онда анықтауыштың өзі де осы 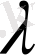санына көбейтіледі.

Айталық, мысалы, екінші жолдың элементтері 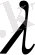санына көбейтіледі дейік. Бұл анықтауыштың мәнін 2-анықтама бойынша жазып, оны алғашқы анықтауыштың мәнімен салыстырайық. Сонда

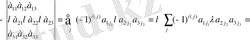
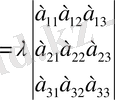
5) Қасиетті былай да айтуға болады: бір жолдың э. лемеңттер. інің. ортақ көбейткішін анықтауыштаң басының алдына шығаруға болады.

6) Егер анықтауыштың екі жолының элементтері пропорционал болса, ондай анықтауыш нольге тең болады.

Алынған анықтауыштың қайсыбір екі жолының элементтері пропорционал болсын. 5) қасиет бойынша пропорционалдық коэффициентті анықтауыш таңбасының алдына шығаруға болады. Сонда қалған анықтауыштың екі жолы бірдей болып шығады да, 4) қасиет бойынша ол нольге тең болады. Сондықтан берілген анықтауыш та нольге тең болады.

7) Егер анықтауыштың і-інші жолының элементтері екі қосылғыштың қосындысы түрінде жазылса, яғни

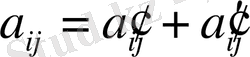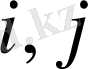( = 1, 2, 3)

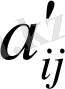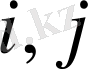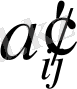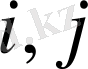болса, ондай анықтауыш екі анықтауыштыц қосындысына тең болады. Бұл анықтауыштардьщ і-інші жолынан өзгелері берілген анықтауыштың жолдарындай, ал олардың біріншісінің і-інші жолы ( =1, 2, 3) элементтерінен (бірінші қосылғыштардан), екіншісінің і-інші жолы ( =1, 2, 3) элементтерінен (екінші қосылғыштардан) тұрады.

Айталық, алынған анықтауыштың, мысалы, екінші жолының элементтері екі қосылғыштардың қосындылары түрінде болып келсін. Сонда 2-анықтаманы пайдаланып және де оңай түрлендірулерді орындағаннан кейін былай жазамыз

8) Егер анықтауыштың қайсыбір жолының элементтеріне басқа жолдың барлық элементтерін бір ғана 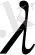санына көбейтіп сәйкес түрде қосса, одан анықтауыштың шамасы өзгермейді.

Мысалы, і-інші жолдың элементтеріне 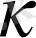-сыншы жолдың сәйкес элементтерін 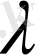санына көбейтіп қосайық. Сонда жаңадан шыққан анықтауыштың 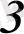-інші жолының элементтері 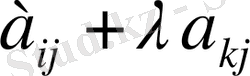(j=1, 2, 3) түрінде жазылады. 7) қасиет бойынша жаңа анықтауыш екі анықтауыштың қосындысына тең болады, сонда оның біріншісі берілген анықтауышпен бірдей де, ал екіншісінің 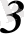нші жолы мен 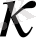-сыншы жолы пропорционал (пропорционалдық көэффициенті 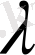санына тең) болады, демек, бұл да нольге тең ((6) қасиет бойынша) . Олай болса, жаңа анықтауыш алынған анықтауышпен тең болады.

Алгебралық толықтауыштар және минорлар. Анықтауышты жолдың не бағанның элементтері бойынша жіктеу.

1-анықтама. Үшінші ретті анықтауыштьщ (11) өрнегіндегі (3-п. ) 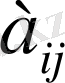элементін қамтитын мүшелерін бір бөлек топтап, жақша сыртына 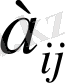элементін шығарғаннан кейін жақша ішінде қалатын өрнекті 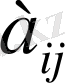элементінің алгебралық толықтауышы деп атайды және оны А арқылы белгілейді.

Мысалы, (11) өрнекте а ₂₃ элементін қамтитын мүшелер а ₁₂ а ₂₃ а ₃₁ және (- а ₁₁ а ₂₃ а ₃₂ ) . Сондықтан,

А ₂₃ =а ₁₂ а ₃₁ - а ₁₁ а ₃₂ .

2-анықтама. Үшінші ретті анықтауыштыц 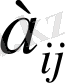элементіні миноры М деп берілген анықтауыштың i-інші жолын және j -інші бағанын сызып тастаганда шығатын екінші ретті анықтауышты айтады.

Мысалы,

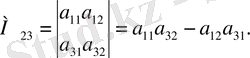
Жоғарыдағы А ₂₃ пен М ₂₃ мәндерін салыстырып, А ₂₃ =-М ₂₃ болатындығын байқаймыз.

Жалпы алғанда қайеыбір элементтіқ алгебралық толықтауышы сол элемент тұрған жол мен бағанның нөмірлерінің қосындысы жұп болғанда плюс таңбамен алынған, ал бұл қосынды тақ болғанда минус таңбамен алынған сол элементтің минорына тең болатынын тексеруге болады, яғни

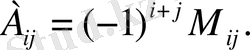(13)

Теорема. Анықтауыштың қайсыбір жолының (бағанының) элементтерінің өздеріне сәйкес алгебралық толықтауыштар мен көбейтшділерініц қосындысы анық-тауыш шамасына тең болады.

Анықтауыштьщ бір жолының (бағанының) элементтерінің басқа жолдың (бағанның) сәйкес элементтерінің алгебралық толықтауыштары мен көбейтінділерінің қосындысы нольге тең болады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.