Аналитикалық геометрия элементтері: векторлар және оларға қолданылатын сызықтық операциялар


АНАЛИТИКАЛЫҚ ГЕОМЕТРИЯ ЭЛЕМЕНТТЕРІ
ВЕКТОРЛАР ЖӘНЕ ОЛАРҒА СЫЗЫҚТЫҚ АМАЛДАР ҚОЛДАНУ
1. Алдын ала ескерту. Осы аталып отырған құралдың алғашқы параграфтары мектепте өтілетін геометрия курсына негізделіп отыр. Сондықтан да оларды сол курстың әрі қарайғы жалғасы деп қарастыру орынды. Енді бағыт деп (түзу бойындағы, жазықтықтағы не кеңістіктегі болсын) бір ғана сәулемен бағыттас болып келетін барлық сәулелердің жиынтығын айтатынын ескерте кетеміз. Сонымен, бағытты қашан да тек бір ғана сәуленің көмегімен көрсетеді.
2. Векторды анықтау. Түзу кесіндісі екі нүктемен - ұштарымен - көрсетіп беріледі» Егер де кесіндінің ұштары реттелген пар нүктелер ретінде қарастырылатын болса, ондай кесіндіні бағытталған кесінді деп атайды.
Бағытталған кесіндіні АВ деп белгілеп, оның ұшы А нүктесі - бастапқы (бірінші), ал В ұшы - соңғы (екінші) нүктесі деп саналады. Сонда бағытталған АВ мен ВА кесінділер әр басқа екендігі түсінікті.
Бағытталған АВ мен ВА кесінділердің әрқайсысын екіншісіне қарама-қарсы кесінді деп атайды.
Қандай болмасын А нүктесін бағытталған кесіндінің бас нүктесі мен ұшы беттесіп жатқан дербес жардай ретінде қарастыру қолайлы келеді.
Оны АА деп белгілеп, бағытталған нольдік кесінді деп атайды.

Нольдік емес бағытталған АВ кесіндінің бағыты АВ сәулесімен бағыттас келеді. Нольдік АА кесіндінің белгілі бағыты болмайды. Егер АВ мен СD сәулелері бірдей (қарама-қарсы) бағытталған болса, онда нольдік емес бағытталған АВ мен СD кесінділерін бірдей (қарама-қарсы) бағытталған деп атайды.
1-анықтама. Вектор деп (түзу бойындағы, жазықтықтағы не кеңістіктегі) бағытталған кесіндіні атайды. Дербес жағдайда бағытталған нольдік кесіндіні нольдік вектор деп атайды.
Нольдік емес векторды не бағытталған кесінді ретінде АВ символымен (А мен В нүктелері алынған бағытталған кесіндінің сәйкесінше бас нүктесі мен ұшы), не латыннын, бір ғана кіші әрпімен, мысалы а, белгілейді. Нольдік векторды АА не 0 деп белгілейді. АВ сәулесімен анықталатын бағыт АВ векторының бағыты деп аталады, ал \АВ\ ара қашықтығы АВ векторының \АВ\ ұзындығы деп аталады. Нольдік вектордың белгілі бағыты болмайды, ал оның ұзындығы нольге тең деп есептеледі.
2-анықтама. Нольдік емес екі векторды, олар бірдей бағытталған болып және ұзындықтары тең болса, тең векторлар деп атайды. Барлық нольдік векторлар тең деп саналады.
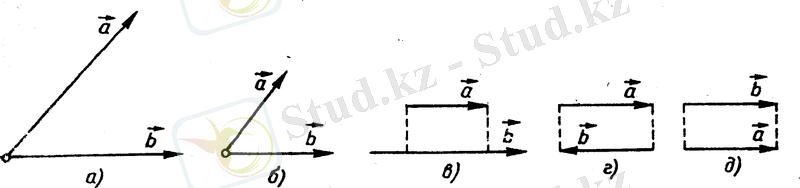
Тең векторлар үшін қабылданған анықтамадан мынадай ұйғарым тікелей шығады: кез келген а векторы мен кез келген А нүктесі үшін а векторына тең болып, басы А нүктесінен шығатын АВ векторы бар болады және ол біреу ғана. Ондайда а векторы А нүктесінен бас-тап салынған делінеді. Былайғы жерде әр басқа нүктелерден бастап салынған, сондай-ақ бірінен-бірі параллель көшіру арқылы шығатын тең екі векторды бөліп ажыратпайтын боламыз. 1-суретте әр басқа А мен А 1 нүктелерінен бастап салынған бір ғана а векторы кескінделген (а = АВ = А 1 В 1 ) .
3-анықтама Бағытталған ВА кесіндісін (бағытталғаи нольдік емес АВ кесіндісіне қарама-қарсы) АВ = a векторына қарама-қарсы вектор деп атайды және (- а) деп белгілейді.
Қарама-қарсы екі вектор қарама-қарсы бағытталған да, ал олардың ұзындықтары тең екендігі түсінікті.
2а, б, в, г-суреттерде тең емес а мен b векторлар кескінделген де, ал 2д-суретте тең а мен b векторлар кескінделген.
3. Векторларды қосу. Екі вектордың қосындысы деп мына ереже бойынша анықталатын векторды айтады.
Үшбұрыш ережесі. Кез келген а және b екі вектордың а + b қосындысы деп кез келген А нүктесінен бастап а=АВ, ал В нүктесінен бастап b = ВС салынған векторларды тұйықтайтын с=АС векторын айтады (3 а-сурет) және былай жазады:
а + b = с немесе АВ + ВС = АС. (1)
А, В, С нүктелерінің үшеуі де бір түзуге тиісті болғанда да (3 б, в-сурет), сонымен бірге олардың кез келген екеуі не тіпті үшеуі де беттесе түскен жағдайда да үшбұрыш ережесі өз күшін жоймайды.

Қосудың қасиеттері:
1° а + b = b + а (ауыстырымдылық қасиеті) ;
2° (а + b ) + с = а + (b + с) (терімділік қасиеті) ;
3° кез келген а векторы үшін а + 0 = а болатындай нольдік 0 векторы бар болады (нольдік вектордің ерекше ролі) ;
4° кез келген а векторы үшін а+( - а) = 0 болатындай қарама-қарсы (- а) векторы бар болады.
Соңғы екі қасиеттің дәлелдемесін келтірейік. 3°-қасиетті дәлелдеу үшін қандай бір А нүктесінен бастап қалауымызша алынған а векторын өлшеп саламыз, айталық, а = АВ. Кез келген нүктені (мысалы, В нүктесін) нольдік вектор деп алуға болатындықтан, 0=ВВ деп келісейік. Енді үшбұрыш ережесін қолдану ғана қалды ((1) теңдік), сонда
а + 0 = АВ + ВВ = АВ = а
Кез келген а векторы үшін а + 0 = а болатындай нольдік 0 векторының бар болатындығын 3°-қасиеттен аңғарамыз.
4°-қасиетті дәлелдеу үшін қандай бір А нүктесінен бастап қалауымызша алынған нольдік емес а векторын өлшеп салайық және де а = АВ делік.
3-анықтама бойынша ( - а) =ВА шығады. (1) ережені қолданып, мынаны табамыз
а + (-а ) = АВ + ВА= АА = 0.
1-қасиетті дәлелдеу үшін бір ғана 0 нүктесінен бастап а = ОА мен b = ОВ векторларын өлшеп салып және де ОВСА параллелограмын құрамыз
(4-сурет) . Векторлардын теңдігі жөніндегі 2-анықтама бойынша:
ВС = ОА = а, АС = ОВ = b .
Үшбұрыш ережесін екі қайыра қолданып мынаны табамыз (сәйкесінше ОАС және ОВС үшбұрыштарын қараңыз)
а+ b = ОА+АС=ОС.
b + а= ОВ + ВС = ОС,
яғни 1 0 - қасиет дұрыс болып қала береді.
Ескерту. Осы тұста векторларды қосу амалының тағы бір параллелограмм ережесі делінетін ереже негізделіп отыр: егер бір ғана 0 нүктесінен бастап
а = ОА мен b = ОВ векторларын салып және бұларға ОВСА параллелограмын құрсақ (4-сурет), онда сол О нүктесінен шығатын диагональ бойымен бағытталған ОС векторы а + b немесе b + а қосындысы болып табылады.
Ескерте кетеміз, А мен В нүктелері бір түзу бойында жатқан жағдай үшін параллелограмм ережесі қолданылмайды. Бұл жағдайда а+ b қосындысына анағұрлым жалпы түрдегі үшбұрыш ережесі бойынша табады.
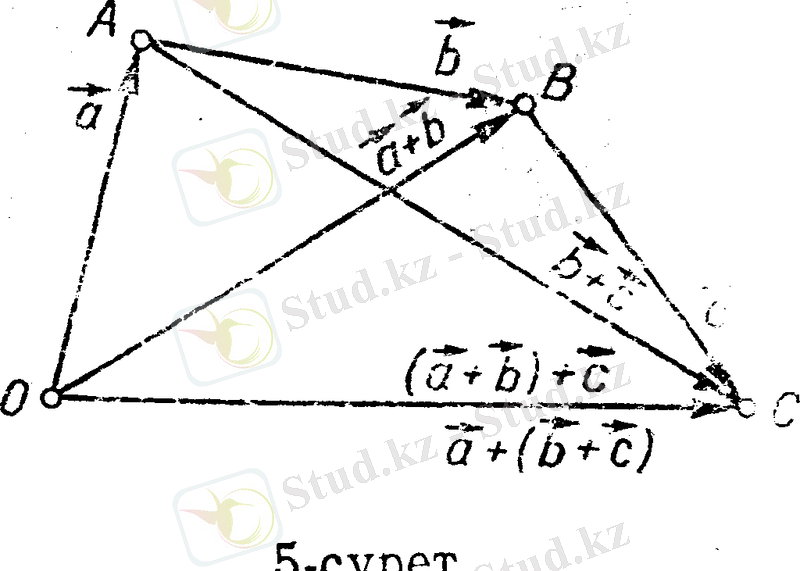
2°-қасиетті дәлелдеу үшін а векторын қалауымызша алынған О нүктесінен бастап салып, а векторының ұшынан бастап b векторын, ал b векторының ұшынан бастап с векторын саламыз (5-сурет) . Айталық, а, b , с вектор-ларының ұштары сәйкесінше А, В, С нүктелері болсын. Сонда
(а + b ) +с = (ОА + АВ) +ВС=ОВ + ВС = ОС.
 а +( b
+с) =
ОА +(АВ +ВС) =ОА +АВС = ОС.
а +( b
+с) =
ОА +(АВ +ВС) =ОА +АВС = ОС.
Сонымен, 2-қасиет дәлелденді.
Жоғарыда дәлелденген қасиеттерге негізделіп саны үшеу және одан да көп векторлардың қосындысы ұғымын енгізу мүмкін болады.
2°-қасиет бойынша (а + b ) +с = а+( b + с) . Осы екі қосындының қай-қайсысын да үш а, b, с векторлардың қосындысы дейді және а + b +с деп (жақшасыз) белгілейді.
 Саны төртеу және одан да көп векторлардың қосындысы да осылайша анықталады. Нақты сандарды қосқандағы-дай, қосылғыштардың орнын ауыстыруға, оларды топтастыруға болады. Сонымен бірге, табылған аралық нәтижеге көңіл аударудың қажеті жоқ.
Саны төртеу және одан да көп векторлардың қосындысы да осылайша анықталады. Нақты сандарды қосқандағы-дай, қосылғыштардың орнын ауыстыруға, оларды топтастыруға болады. Сонымен бірге, табылған аралық нәтижеге көңіл аударудың қажеті жоқ.
Бірнеше векторларды (саны шектеулі) қосу мынадай тұйықтау ережесі бойынша орындалады.
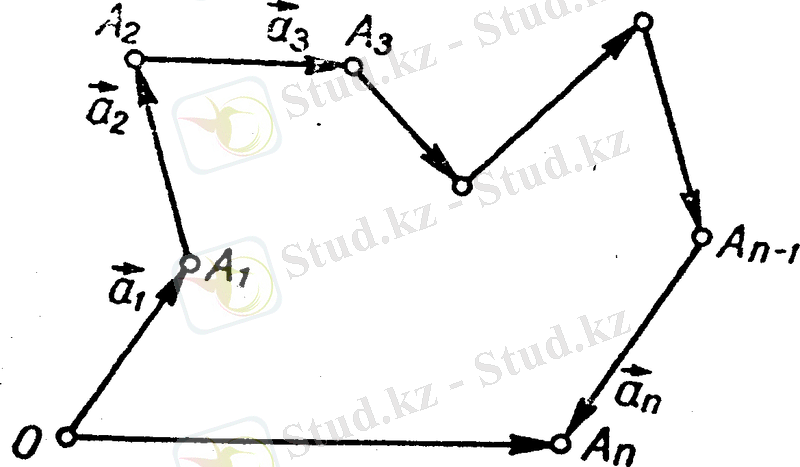
Көпбұрыш ережесі. а 1 , а 2 . . . , а п векторларының а 1 + а 2 + . . . + а п қосындысы деп кез келген О нүктесінен бастап салынған а 1 = ОА 1 , А 1 нүктесінен бастап а 2 = А 1 А 2 т. с. с. А п- 1 нүктесінен бастап а п =А п - 1 А п векторларын тұйықтайтын ОА п векторын атайды (6-сурет) және былай жазады:
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz