БОЛАШАҚ МАТЕМАТИКА МАМАНДАРЫН ДӘРЕЖЕЛІК ФУНКЦИЯЛАРЫ БАР ТЕҢДЕУЛЕР МЕН ТЕҢСІЗДІКТЕРДІ ШЕШУГЕ ТЕРЕҢДЕТЕ ОҚЫТУ ӘДІСТЕМЕСІ

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 29 бет
Таңдаулыға:

ӘОЖ 378.147:514.18(574) Қолжазба
құқығында

Алпысов Ақан Қанапияұлы

БОЛАШАҚ МАТЕМАТИКА МАМАНДАРЫН ДӘРЕЖЕЛІК ФУНКЦИЯЛАРЫ БАР ТЕҢДЕУЛЕР МЕН
ТЕҢСІЗДІКТЕРДІ ШЕШУГЕ ТЕРЕҢДЕТЕ ОҚЫТУ ӘДІСТЕМЕСІ

13.00.02 – Оқыту және тәрбиелеу теориясы мен әдістемесі
(математика)

Педагогика ғылымдарының кандидаты
ғылыми дәрежесін алу үшін дайындалған диссертацияның
авторефераты

Қазақстан Республикасы
Алматы, 2006

Жұмыс Павлодар мемлекеттік педагогикалық институтында орындалды

Ресми оппоненттер: педагогика ғылымдарының докторы,
профессор Қағазбаева Ә. К.

педагогика ғылымдарының
кандидаты,
доцент Қаңлыбаев Қ.И.

Жетекші ұйым: Л.Н. Гумилев атындағы Еуразия
Ұлттық университеті

Қорғау 2006ж. ___________ күні сағ.______Абай атындағы Қазақ
ұлттық педагогикалық университетіндегі педагогика ғылымдарының
докторы ғылыми дәрежесін беру жөніндегі Д 14.08.05. диссертациялық
кеңесінде өтеді.
Мекен жайы:050012,Алматы қаласы,Төле би көшесі,86,4-қабат,413-бөлме.

Диссертациямен Абай атындағы Қазақ ұлттық педагогикалық университетінің
кітапханасында танысуға болады.

Автореферат 2006 жылы _____________________ таратылды.

Диссертациялық кеңестің
ғалым хатшысы Ж.Ә.Шоқыбаев

Жұмыстың жалпы сипаттамасы

Зерттеудің өзектілігі. Білім беру саласындағы Мемлекеттік саясаттың
негізгі бағыттары және оларды іске асырудың жолдары Қазақстан
Республикасының білім беруді дамытудың 2005-2010 жылдарға арналған
мемлекеттік бағдарламасында айқындалған. Негізгі мақсат – адам ресурстарын
даярлау сапасын арттыру, жеке тұлға мен қоғамның қажеттіліктерін
қанағаттандыру үшін Қазақстан Республикасының 2010 жылға дейінгі
стратегиялық даму жоспарының басымдылықтары негізінде көп деңгейлі білім
берудің ұлттық жүйесін жаңарту. Осыған орай Қазақстан Республикасының 2015
жылға дейінгі Концепциясының басты мақсаты ретінде сапалы білім беру
негізінде білікті жеке тұлғаның қалыптасуын қамтамасыз ететіндей жеке
білім беру жобасына көшу мәселесі қойылған. Аталған Концепция жас ұрпаққа
қазіргі талапқа сай оқытудың жаңа ақпараттық технологияларын енгізуге
бағытталуын көздейді.
Қазақстан Республикасының Білім туралы заңында және оқу-тәрбие
саласына байланысты басқа да құжаттарда жоғары оқу орындарында жан-жақты
білімді, ой-өрісі кең, мәдениеті жоғары, жаңаша ойлауға қабілеті бар,
әлемдік озық технологиялардан хабардар, еліміздің жарқын болашағын ойлайтын
қазіргі өмір талабына сай іріктелген таңдаулы мамандарды даярлау
қажеттілігі көрсетілген. Мұндай талаптар болашақ математика мамандарын
даярлауды түбегейлі жетілдіруді талап етеді, өйткені алдағы реформадағы
басты тұлға мұғалім болып табылады, сондықтан да жаңа формацияның
педагогтарын даярлау бүгінгі күннің негізгі мәселелерінің бірі болып
табылады.
Болашақ математика мамандары жоғары мектеп қабырғасынан жан-жақты және
іргелі білім жүйесін алуы қажет. Болашақ мамандарды іргелі білім
жинақтаған, жан-жақты дамыған тұлға ретінде дайындау түрлі бағыттар арқылы
жүргізіледі: оқу жоспарларының мазмұнын жетілдіру, ғылыми-әдістемелік
қамтамасыздандыруды жүзеге асыру, ғылыми парасаттылық, оқытушы-
педагогтардың біліктілігін көтеру және т.б.
Бүгінгі таңдағы оқу-ағарту саласының қалыптасуы мен дамуының
дидактикалық негіздерін зерттеуге көптеген әдіскер ғалымдар өз үлестерін
қосуда. Соның ішінде С.И.Архангельский, Ю.К. Бабанский, В.П.Беспалько,
Т.А.Ильина, Н.В.Кузьмина, Л.П.Гримак және т.б. еңбектерінің орны ерекше.
Оқыту үрдісіндегі зерттеу жұмысын басқару, оқырмандардың шығармашылық
және танымдық қабілеттерін дамыту негізінде сабақтың тиімділігін арттыру
мәселелері педагог-психолог ғалымдар: П.Я.Гальперин, В.А. Гусев, В.А.
Крутецкий, А.Н.Леонтьев, С.Л. Рубинштейн, Н.Ф.Талызина, Л.М.Фридман және
т.б. еңбектерінде қарастырылды.
Білім беру жүйесінде әлемдік деңгейге жету үшін жасалынып жатқан
талпыныстар бағытында студенттердің танымдық ізденімпаздығын дамыту
теориясын қалыптастыруда педагог-әдіскер А.Е.Әбілқасымованың, И.Б.
Бекбоевтың, Т.С. Садықовтың еңбектерін ерекше атауға болады.
Ә.К. Қағазбаеваның, М.Е.Есмұқановтың зерттеулерінде жоғары
педагогикалық оқыту жүйесінде болашақ математика мұғалімдерінің әдістемелік
даярлықтарын жетілдірудің теориялық-технологиялық негіздері қарастырылған.
Жоғары оқу орындарында студенттердің математикалық дайындығын
жетілдіру мәселелері, оқытудың сапасын көтеру проблемасы ТМД және
республикамыздың әдіскер ғалымдары Т.В. Кудрявцев, В.И. Крупич, Э.М.
Мамбетакунов, В.А. Далингер, Л.М. Фридман, П.М. Эрдниев, А.Е. Әбілқасымова,
Е.Ғ. Балыбердина, И.Б. Бекбоев, В.П. Добрица, М.Е. Есмұқан, Ә.К.
Қағазбаева, Д. Рахымбек және т.б. еңбектерінде қарастырылған.
Көптеген психолог ғалымдардың зерттеулері оқыту үрдісінде білімді
қалыптастыру және дамыту проблемаларына арналды. Соның нәтижесінде дәстүрлі
оқыту жүйесін зерттеуші психологтардың, яғни П.Я.Гальперин мен
Н.Ф.Талызинаның Ой амалдарын сатылап қалыптастыру, Е.Н.Кабанова-Меллер,
Д.Н.Боявленская, А.А.Менчинская, Л.С.Выгодский, Л.Б.Ительсонның классикалық
теорияларына сүйеніп жүргізді. Олардың зерттеулерінде әдістемелер
балалардың жас ерекшеліктеріне байланысты білімді қабылдау заңдылықтарына
сүйенгенде нәтиже беретіндігі пайымдалған. Ал білім көзі оқулық. Оқулықта
не жазылса, оқырман санасында қалыптастыратын білімнің көлемі де,
біліктіліктің кеңістігі де сол. Сондықтан да білім беруді жетілдіру
бағытында оқулықтар мазмұны мен құрылымын жетілдіру мәселесінің күн
тәртібінен түспейтіні де сондықтан.
Әрбір он-онбес жылдарда оқулықтар өзгеріп отыруы заңдылыққа айналды.
1986-1990 жылдары Педагогика ғылымдарының академиясы мен оқулық иегерлері
бағытты жұмыстар жүргізді. А.Н.Колмогоров, А.Н.Тихонов, А.В.Погорелов,
С.А.Теляковский сияқты академиктермен Л.С.Атанасян және т.б, Ю.М.Колягин,
М.И.Башмаков тағы да сол сияқты профессорлар, ғылым докторлары математиканы
оқытудың мазмұны мен әдістемесін жетілдіру туралы ойларын ортаға салды.
Мектептегі математика пәнін жаңа талапқа сай оқытуды жетілдіру
мәселелері оның өзекті бірнеше идеялық желілерінің құрылымы мен оларды
оқыту әдістемелерін жетілдірумен тығыз байланысты. Сондай желілердің бірі
мазмұнды-қолданбалық маңызы бар теңдеулер мен теңсіздіктер желісі.
Теңдеулер мен теңсіздіктерге байланысты материалдар мектеп курсы
математикасының мазмұнының қомақты бөлігін құрайды, себебі теңдеулер мен
теңсіздіктер математиканың түрлі салаларында және маңызды қолданбалы
есептерді шығаруда кең қолданыс табады. Сондықтан да оқушыларды теңдеулер
мен теңсіздіктер желісінің қолданбалық, теориялық-математикалық және
математика курсының басқа да мазмұндық желілермен байланысын құру
бағыттарын игерту мәселесі теңдеулер мен теңсіздіктерді шешуге үйрету
материалдарын талдау мен синтездеу деңгейінде саналы игерту мәселесімен
тығыз байланысты.
Математиканы дәстүрлі оқыту жүйесінде теңдеулер мен теңсіздіктерді
оқытудың нәтижелеріне талдау жасау келесідей кемшіліктердің бар екеніне көз
жеткізді:
- оқушылардың теңдеулер мен теңсіздіктерді шешу әдістерін игеру
барысында олардың қолданыс табуының болашағын болжай алмайтындығын;
-теңдеу мен теңсіздіктерді шешу әдістерінің біртұтас жүйе екендігіне
көзқарастың қалыптаспайтындығын;
- теңдеулер мен теңсіздіктер шешу әдістерінің математиканың негізгі
желілер мазмұнымен байланысын күшейтетініне көздерінің жете
бермейтіндігін;
- теңдеулер мен теңсіздіктерді шешу әдістерін бағытты игертуге терең
мән берілмейтіндігін т.с.с. Бұл кемшіліктер қазіргі таңда оқушылардың
математикаға деген қызығушылығының төмендеуінің бірден – бір себебі деп
айтуға болады.
Ал математиканың мазмұнын оқушыларға саналы да, сапалы да меңгерту
мәселесі математика мұғалімдерінің математикалық білімдерінің тереңдігіне,
әдістемелік шеберлігіне, шығармашылық қабілеттеріне тікелей байланысты
екендігі ешбір күмән келтірмейді. Болашақ математика мамандарын жоғары
педагогикалық оқу орындарында даярлауда оның математикалық дайындығына
математика пәндерін, ал әдістемелік дайындығына Есептер шығару практикумы
мен Математиканы оқыту теориясы мен әдістемесі пәндерін оқытудың алатын
орны зор. Жоғары оқу орындарында болашақ математика мұғалімдерін
дайындаудағы қазіргі таңдағы кемшіліктердің негізгілерінің бірі аталған
пәндерді оқытуда-болашақ математика мұғалімдерін мектеп математика курсының
негізгі идеялық өзекті желілеріне бағытты дайындау мәселесіне жете көңіл
бөлінбейтіндігі. Сондықтан да мектеп математика курсында теңдеулер мен
теңсіздіктерді оқытуды жетілдіру мен жоғары оқу орындарында болашақ
математика мамандарын бағытты даярлау қажеттілігі Болашақ математика
мамандарын дәрежелік функциялары бар теңдеулер мен теңсіздіктерді шешуге
тереңдете оқыту әдістемесі атты зерттеу тақырыбымыздың өзектілігін
көрсетеді.
Зерттеудің мақсаты: Болашақ математика мамандарын теңдеулер мен
теңсіздіктерді шешуге тереңдете оқыту әдістемесінің бір нұсқасын жасау.
Зерттеу нысаны: Жоғары оқу орындарында болашақ математика мамандарын
даярлау үрдісі.
Зерттеу пәні: Болашақ математика мамандарын математиканың жалпыланған
заңдылықтары негізінде дәрежелік функциялары бар теңдеулер мен
теңсіздіктерді шешуге тереңдете оқыту әдістемесін қалыптастыру жолдары.
Зерттеудің ғылыми болжамы: Егер де болашақ математика мамандарын
математиканың жалпыланған заңдылықтары негізінде теңдеулер мен
теңсіздіктерді шешуге тереңдете оқытуды бағытты жүзеге асырсақ, онда
студенттер теңдеулер мен теңсіздіктерді шешудің тиімді әдістерін күрделі
есептер шығару барысында игереді және теңдеулер мен теңсіздіктер желісі
материалдарын синтездік деңгейде меңгеріп, олардың есептер шығарудағы
шығармашылық қабілеттері артады.
Зерттеудің міндеттері. Зерттеудің мақсатына, пәніне және болжамына
сәйкес зерттеу барысында мына міндеттерді шешу керектігі айқындалды:
- теңдеулер мен теңсіздіктерді шешудің тиімді әдістерін дидактикалық-
әдістемелік тұрғыдан негіздеу;
- болашақ математика мамандарын дәрежелік функциялары бар теңдеу мен
теңсіздіктерді шешуге тереңдете оқыту әдістемесін құру;
- болашақ математика мамандарын дәрежелік функциялары бар теңдеу мен
теңсіздіктерді шешуге тереңдете оқыту әдістемесін педагогикалық тәжірибеден
өткізіп, ғылыми болжамның дұрыстығын дәлелдеу.
Зерттеудің теориялық негіздері. Атақты психологтар С.Л.Рубинштейн,
Л.С.Выготский, В.В.Давыдов, Л.В.Занков, Д.В.Эльконин, Л.М.Фридман,
П.А.Шеваревтың ой-өрісті дамытуға бағытталған теориялық еңбектері,
американың әлемге әйгілі математигі және педагогі Д.Пойаның Математика
және шындыққа ұқсас ой қорытулар, Математикалық жаңалықтар, Есепті
қалай шешу керек деген кітаптарындағы әдістемелік идеялары, П.М.Эрдниев,
Б.П.Эрдниевтердің Математиканы оқытудағы дидактикалық бірліктерді
ірілендіру кітабындағы әдістемелік қағидалар және М.Е.Есмұқанның
Құрылымдық әдіспен оқушылардың математикалық білімін қалыптастырудың және
ойлау қабілетін дамытудың психологиялық-педагогикалық негіздері атты
докторлық диссертациясындағы әдістемелік идеялар, А.Е.Әбілқасымова,
Ә.К.Қағазбаеваның жоғары оқу орындарында болашақ математика мамандарының
өзіндік танымдық қызметтерін қалыптастыру теориясы мен кәсіптік әдістемелік
даярлықтарын жетілдіру идеялары.
Зерттеудің әдіснамалық негіздері - Қазақстан Республикасының Білім
туралы заңы, математикалық білім беру стандарты, Қазақстан Республикасында
білім беруді дамытудың 2005-2010 жылдарға арналған Мемлекеттік
бағдарламасы, оқу - әдістемелік кұралдар, бағдарламалар, педагогтардың,
психологтардың және әдіскерлердің еңбектері.
Зерттеу үш кезеңде жүргізілді.
Бірінші кезеңде (1995-1998) зерттеу мәселесі бойынша психологиялық-
педагогикалық және әдістемелік әдебиеттерге шолу жасалынды. Зерттеудің
теориялық негіздері анықталды. Мектеп мұғалімдерінің тәжірибелерімен танысу
жүзеге асырылып, олардың білім қалыптастыру үрдісіндегі қызметтеріне талдау
жасалып, кемшіліктер айқындалып, ақпараттық технологияны енгізу қажеттігі
негізделді.
Екінші кезеңде (1998-2000 ж.) эксперимент бағдарламасы жасалды және
теңдеулер мен теңсіздіктерді шешудің тиімді әдістерін дидактикалық
әдістемелік тұрғыдан негіздеу жүзеге асырылды.
Үшінші кезеңде (2000-2005 ж.) болашақ математика мамандарын дәрежелік
функциялары бар теңдеу мен теңсіздіктерді шешуге тереңдете оқыту
әдістемесін құру жүзеге асырылып, құрылған әдістемелік жүйе педагогикалық
тәжірибеден өткізіліп, негізгі қорытындылар және зерттеу нәтижелерін ендіру
бойынша ұсыныстар тұжырымдалды, жұмысты дайындау аяқталды.
Зерттеу жүргізілген тірек оқу орындары. Ғылыми – зерттеу жұмыстары
Павлодар Мемлекеттік педагогикалық институтында, С.Торайғыров атындағы
Павлодар Мемлекеттік университетінде, Абай атындағы ҚазҰПУ-де, Павлодар
қаласындағы №10, №42 орта мектептерінде жүргізілді.
Зерттеу әдістері. Зерттеу тақырыбына байланысты философиялық,
психологиялық, педагогикалық әдістемелік теорияларға байланысты
әдебиеттерге талдау жасау; зерттеу тақырыбы бағытындағы орындалған
диссертациялық және монографиялық еңбектермен танысу; алдыңғы қатардағы
әдіскерлердің озық тәжірибелерін зерделеу; мектеп оқушыларының, жоғары оқу
орындары студенттерінің теңдеулер мен теңсіздіктер желісі материалдарын
игеру деңгейлерін сараптау; теңдеулер мен теңсіздіктерді шешуді тереңдете
оқыту заңдылықтарын зерттеу негізінде жаңа ұғымдық аппарат жүйесін құру,
соның негізінде тиімді әдістер жүйесін енгізу.
Зерттеудің ғылыми жаңалығы мен теориялық мәнділігі:
- теңдеулер мен теңсіздіктерді шешу әдістерін жетілдіру жолдары
қарастырылды;
- жоғарғы ретті теңдеу мен теңсіздіктер құрылымы тұрақты функцияларды
енгізу арқылы дәрежелері төмен екі теңдеу жүйелеріне жіктеліп оқырманға
белгілі квадрат теңдеулерді шешуге келтіретін әдіс енгізілді;
- теңдеулер мен теңсіздіктерді шешудің әдістері ретінде кері амалдар
әдісі мен теңдеулер мен теңсіздіктерді сығыстыра оқыту әдістемесі
енгізіліп, олардың тиімділігі дәлелденді;
- болашақ математика мамандарын дәрежелік функциялары бар теңдеу
мен теңсіздіктерді шешуге тереңдете оқытудың әдістемелік негізі жасалды.
Зерттеудің практикалық құндылығы. Теңдеулер мен теңсіздіктерді шығару
әдістерінің дидактикалық -әдістемелік негіздерін айқындау негізінде болашақ
математика мамандарын дәрежелік функциялары бар теңдеу мен теңсіздіктерді
шешуге тереңдете оқыту әдістемесі жасалынып, ол әдістемелік жүйенің оқыту
үрдісіндегі тиімділігі дәлелденді.
Қорғауға ұсынылатын қағидалар:
- болашақ математика мамандарын дәрежелік функциялары бар теңдеулер мен
теңсіздіктерді шешудің дәстүрлі емес әдістерін және оларды оқу үрдісінде
қолданудың әдістемелік негіздері;
- жоғарғы ретті теңдеулер мен теңсіздіктерді сығыстыра оқыту
әдістемесі;
- болашақ математика мамандарын дәрежелік функциялары бар теңдеулер мен
теңсіздіктерді шешуге тереңдете оқыту жүйесінің әдістемелік негіздемелері;
- болашақ математика мамандарын дәрежелік функциялары бар
теңдеулер мен теңсіздіктерді дәстүрлі емес әдістермен шешу жолдарын игерту
әдістемесінің тиімділігін көрсететін педагогикалық эксперименттің
нәтижелері.
Зерттеу нәтижелерінің дәлелділігі мен сенімділігі – педагогика
ғылымының жетістіктеріне сүйене отырып, алынған қорытындылар мен нақты
нұсқаулардың психологиялық–педагогикалық және әдістемелік зерттеулер
нәтижелеріне сәйкестігімен және олардың теориялық, әдіснамалық тұрғыдан
негізделуімен, зерттеу әдістерінің тиімді пайдалануымен, теориялық
мәселелердің объективті тұрғыдан талдануымен, сол сияқты жүргізілген
педагогикалық–эксперименттің нәтижелерімен қамтамасыз етілген.
Зерттеу нәтижелерін сынақтан өткізу және ендіру эксперимент барысында
жүзеге асырылды. Зерттеу нәтижелері С.Торайғыров атындағы ПМУ-нің Сәтбаев
оқулары атты жас ғалымдар, студенттер және оқушылардың ғылыми
конференцияларында (2002ж.), Ш.Уалиханов атындағы Көкшетау мемлекеттік
университетінің Шоқан тағылымы атты халықаралық ғылыми-практикалық
конференцияларында (2003ж, 2004ж, 2005ж), Жоғары кәсіптік білім беру
сапасын арттырудың өзекті мәселелері атты Республикалық ғылыми -
тәжірибелік конференциясында (Қызылорда, 2003 ж) баяндалды. Зерттеудің
негізгі қағидалары мен нәтижелері Павлодар мемлекеттік педагогикалық
институтының алгебра, геометрия және математиканы оқыту әдістемесі
кафедрасы мен Абай атындағы ҚазҰПУ-нің жаңа ақпараттық технологиялар мен
оқыту әдістемелері кафедрасындағы ғылыми-әдістемелік семинарларында
талқыланып, басылым көрген мақалаларда оқу-әдістемелік құралда және әртүрлі
журналдарда зерттеу нәтижелері мен зерттеудің негізгі жағдайлары көрініс
тапты.
Диссертацияның құрылымы. Диссертация кіріспеден, екі бөлімнен, әр
бөлім қорытындылары мен түйіндемеден, пайдаланылған әдебиеттер тізімінен,
суреттерден, кестелерден және қосымшалардан тұрады.
Кіріспеде зерттеу тақырыбының өзектілігі мен маңызы негізделген,
зерттеудің мақсаты мен міндеттері, нысаны, болжамы, әдіснамалық негізі,
ғылыми жаңалығы, зерттеу әдістері мен зерттеу жұмысының негізгі кезеңдері
ашылып көрсетілген, тәжірибелік маңыздылығы мен қорғауға ұсынылатын
қағидалар, зерттеу жүргізілген тірек оқу орындары, зерттеу нәтижелерінің
дәлелділігі, зерттеу нәтижелерін сынақтан өткізу мен тәжірибеге ендіру
жолдары көрсетілген.
Теңдеулер мен теңсіздіктерді шешу әдістерінің дидактикалық-
әдістемелік негіздері атты бірінші тарауда болашақ математика мамандарын
жаңа талапқа сай даярлығын қалыптастырудың педагогикалық-психологиялық
негізі және оқу процесінде теңдеулер мен теңсіздіктерді шешу әдістерінің
дидактикалық-әдістемелік негіздері қарастырылды. Теңдеулер мен
теңсіздіктердің арасындағы логикалық-функциональдық байланыстарды тиімді
пайдалану жолдары көрсетілді. Өзара кері функциялар және олардың арасындағы
байланысты сипаттайтын тепе-теңдік, теңдеуді кері амалдар әдісі арқылы
адамның ойлау жүйесінің заңдылығын зерттеу, теңдеу құрылымын стандарттау
арқылы студенттердің ойлау қабілеттерін қалыптастыру және дамыту, жоғары
ретті теңдеулер мен теңсіздіктерді сығыстыра оқыту әдістемесі
қарастырылды.
Болашақ математика мамандарын дәрежелік функциялары бар теңдеу мен
теңсіздіктерді шешуге тереңдете оқыту әдістемесі атты екінші тарауда
дәрежелік функциялары бар теңдеулер мен теңсіздіктерді шешудің дәстүрлі
емес әдістерін оқу үрдісінде қолданудың әдістемелік негіздері, теңдеулер
мен теңсіздіктерді шешуге тереңдете оқыту жүйесінің әдістемелік
негіздемелері қарастырылды. Квадрат үшмүшеліктердің көбейтіндісіне қатысты
теңсіздіктерді шешу, ұқсас өрнектер құрамынан құрылымы тұрақты функцияны
іздестіру, модуль арқылы біріктірілген квадрат үшмүшеліктердің
графиктерінің өзгерісін зерттеу, иррационал теңсіздіктерді шешу
процессіндегі ой қозғалысының мазмұны сипатталды және нәтижелері
келтірілді. Дәрежелік функциялары бар теңдеулер мен теңсіздіктерді
тереңдете оқытудың әдістері мен құрылымдары жүйелі түрде дайындалып,
қорытындылары іс жүзінде тексерілді.
Қорытындыда жалпы жұмыс мазмұны тиянақталып, зерттеудің нәтижесінде
алынған тұжырымдар мен эксперименттік жұмыс нәтижелері бойынша ұсыныстар
беріліп зерттеудің болашақтағы жолдары көрсетілген.
Қосымшада студенттердің ойлау қабілетін дамыту мақсатындағы нұсқаулар,
тапсырмалар жүйесі, мазмұнды есептер ұсынылды.
Математиканы оқытудың бүгінгі таңдағы жаңа жүйесі мұғалімдердің
әдістемелік даярлықтарына қойылатын талаптар деңгейін көтеріп, жаңа
міндеттер жүктеп отыр. Сондықтан, жоғары білім жүйесінде болашақ математика
мамандарына уақыт талабына сай, шығармашылық негізде дайындау жолдарын
қарастыру қажеттілігі туындайды.
Орта және жоғары мектеп орындарында математиканы оқытудың мақсаты –
оқырмандарға күнделікті өмірде және қазіргі қоғамда пайдалы еңбек еткенде
қажет болатын және де басқа пәндерді оқып меңгеруге, білімін әрі қарай
жалғастыруға толық мүмкіншілік беретін математикалық білім, іскерлік және
дағдылардың негізін берік және саналы түрде меңгеріп алуын қамтамасыз ету.
Зерттеу жұмысында қазіргі таңда алда шешуін талап ететін негізгі
мәселелер айқындалып, білім алушыларға жеке тұлға ретінде қарай отырып,
олардың шығармашылық мүмкіндіктерін, іс-қабілеттерін арттыру мақсатында
оқу үрдісінің мазмұнының іске асырылу жолдарының логикасын қайта қарау,
әсіресе болашақ математика мамандарының кәсіби дайындығын қазіргі заман
талабына сәйкестендіру, теңдеулер мен теңсіздіктер желісінің қолданбалық,
теориялық-математикалық желілерімен байланысын құру бағыттарын игерту,
теңдеулер мен теңсіздіктерді шешуге тереңдете оқыту әдістемесін талдау мен
сапалы меңгерту, теңдеулер мен теңсіздіктерді шешу әдістерін беру кезінде
есептерді тиімді шешу дағдылары мен іскерліктерін дамыту мәселесі
қарастырылды. Мәселенің күрделігі мен қиындығынан туындайтын ғылыми-
әдістемелік шешімдер анықталды.
Жоғары мектепте теңдеулер мен теңсіздіктерді шешуге тереңдетіп оқыту
әдістемесін құру студенттердің теориялық білімдерін нақтылаудың, оларды
есеп шығаруда қолдана алу ептіліктерін қалыптастырудың маңыздылығы
көрсетілді.
Теңдеу нысынасы – функция. Теңдеуді құрастыру мен теңдеуді шешу бір-
біріне қарама-қарсы орындалатын екі процесс. Теңдеуді құрастырушы құрылымы
тұрақты функцияны алып, оны математиканың ережелерін пайдаланып, шешімін
таба алатын теңдеуге қойып, түрлендіріп, күрделі теңдеу алып, оқырманның
білімін арттыру мақсатын көздейді. Теңдеуді шешуші оның құрылымындағы
ақпарға сүйеніп берілген теңдеуді кері бағытта түрлендіріп жасырылған
функцияның құрылымын анықтайды және теңдеудің құрылымын ықшамдап қарапайым
түрге келтіреді. Содан кейін оның шешімін табады. Күрделендіру процесіне
қатысқан функцияның құрылымын анықтамай студент берілген теңдеуді шеше
алмайды. Екі процесті бір-бірімен байланыстыру тура мен кері функциялардың
құрылымын зерттеуден басталды. Екі процесс бірі екіншісімен жалғасып
жатқандықтан тура мен кері функцияның екеуі де бірдей анықталатын облысты
іздеуге және функция мен бейнелеу ұғымдарын біріктіріп қарастыруға
мәжбүрледі. Өйткені теңдеуге қатысатын функцияның өрнегінің құрылымы
өзгереді. Зерттеудің нәтижесінде теңдеудің шешімін табуға бағытталған мына
процестер анықталды.
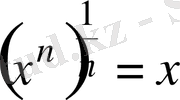(1) және 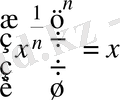(2)
Бұл өзара тура және кері дәрежелік функциялардың арасындағы байланысты
сипаттайтын тепе-теңдік. Өзара кері функциялар тепе-теңдіктерінде тәуелсіз
айнымалының дәрежесін кері дәрежеге немесе оның кері дәрежесін n-ші
дәрежеге шығарғанда тәуелсіз айнымалының өзі шығатындығы тепе-теңдікте
көрсетілген. Графиктік тұрғыдан бірінші ширектің биссектрисасы х-ті n-ші
дәрежеге шығарып содан кейін ол графиктің ординатасын кері амалмен
бейнелегенде биссектрисаның өзі шығады деп қарастырсақ, онда бұл тепе-
теңдіктер, біріншіден әдіске айналады, екіншіден, х-ің қасиетін
сақтайтындығын көрсетеді. Бейнелеу кезінде биссектрисаның екі нүктесі (0;0)
және (1;1) өз орнында қалады. Бұлар қозғалмайтын нүктелер деп аталды.
Қозғалмайтын нүктелердің арасындағы нүктелерді тура функцияның дәреже
көрсеткіші n сығып абсцисса өсіне жақындатады, ал олардан тысқары
орналасқан нүктелерді тура функцияның дәреже көрсеткіші вертикаль түзудің
бойымен созады. (2) тепе-теңдіктегі 1n көрсеткіші оператордың ординатасын
тәуелсіз айнымалының қозғалмайтын екі нүктесін орнында қалдырып, олардың
арасындағы нүктелерді биссектрисаның өспелілік қасиетін сақтап созады.
Қозғалмайтын нүктелерден тысқары жатқан нүктелерді оның дәреже көрсеткіші
тағыда биссектрисаның өспелілік қасиетін сақтап сығады. Егер осы процесті
тік бұрышты координат жүйесінде қарастырсақ, онда тура және кері дәрежелік
функциялар бейнелеу кезіндегі қасиетін өз координат жүйесінде де
сақтайтындығы анықталды. Тікбұрышты координат жүйесінде тек функцияның
координат жүйесі, ал график дәрежелік функцияның өз координат жүйесінде
салынады. Функцияның компоненттерінің (негіз, дәреже көрсеткіш, функция
мәнінің) әрбіреуінің атқаратын қызметтері анықталды және жоғарыда
пайымдалған тепе-теңдік жалпыланды.
Математиканы оқытудағы негізгі мақсат абстракциялық ойлау жүйесін
қалыптастыру. Зерттеудің нәтижесінде анықтағанымыз – адамға абстракциялық
ой процестер арқылы қалыптасады. Осы идеяны зерттеу тақырыбымен
байланыстырып айтсақ, онда жинақталған-жинақталмаған өрнектердің бірінен
екіншісіне көшу (ауысу), нақтыдан жалпыланған және жалпыланған өрнектен
нақты өрнекке ауысу процестерінде қалыптасатындығы анықталды. Осы
процестердің бірінен екіншісіне ауысуды студент өзі іске асырса, онда
абстракциялық ой оның өзіне қалыптасады. Теңдеуді мына түрде берейік:

Талап студенттің ойлау жүйесін көрсету. Алдымен ол теңдеудің
жинақталған құрылымын көпмүшелік түрінде жазып алады: . Жинақталмаған
осы құрылымды теңдеудің нақты құрылымымен салыстырып оның коэффициенттерін
Ньютон биномының формуласын пайдаланып жіктеу керектігін анықтайды. Содан
кейін параметр а-ның мәнін анықтайды. Ақырында, теңдігінен k-ның
мәнін анықтайды. Сонымен ойлау әдістемесін екі мүшеліктің дәрежесі түрінде
жазылған талап басқаратындығы анықталды. Көпмүшеліктің коэффициенттері мен
көрсеткіштерін өзгертсе әдістің тұрақтылық қасиеті сақталады.
Төртінші дәрежелі көпмүшелігі бар теңдеулердің барлығы екімүшеліктің
төртінші дәрежесі түрінде өрнектеле бермейді. Бірақ олар квадрат үшмүшелік
теңдеуінен алынғаны ақиқат. Төртінші дәрежелі теңдеудің дәреже көрсеткішін
төмендету тұрақты функция ұғымын енгізуге және теңдеуді жіктеп теңдеулер
жүйесін құрастыруға келтірді. Жүйенің квадрат теңдеуінің негізгі шешімін
тұрақты функциясы бар теңдікке қойып негізгі теңдеу алынады. Негізгі
теңдеудің бір ғана негізгі шешімі болады.
Теңдеулердің құрылымы өзгергенде талапта өзгереді. Талаптың өзгеру
заңдылығын көрсетелік.
1 –есеп. х4 -3х3 -8х2 + 12х + 16 ( 0 (
Теңдеу құрамындағы ақпарды оқып шешім қабылдау керек. Теңдіктің екі
жағында х2 –қа бөліп дәреже көрсеткіштері бірдей мүшелерді топтасақ, онда
мына теңдеуді аламыз.

Егер белгілеп квадрат дәрежеге шығарсақ, онда келесі
болады. Ал берілген теңдеу келесі есептеу мүмкіншігімізге сай келетін екі
теңдеулер жүйесіне жіктеледі:

.
Нақты теңдеулердің құрылымы сонымен бірге оны жүйеге келтіру
әдістерінің түріндегі ақпар дербестеніп өзгеріп тұрады. Ақпардың дерб-
стену процесін жалпыласақ, онда басқа күрделі теңдеулерді жүйеге келтіруге
байланысты ой туады.
(ж) жүйесіндегі күрделі теңдеудің дәреже көрсеткішін төмендетуге
бағытталған функцияны f(х) -пен, ал квадрат үшмүшеліктің жалпы түрін
жазсақ, онда ойлау жүйесін басқаратын талапты былай жазуымызға болады.

Енді (ж-ж) жүйесі түрлендіруге бағытталған ойымызды басқара алатындығын
көрсетелік.
2 –есеп. (х2 +х+1)2 ( х2 (3х2 + х + 1) ( х ( к?
Есеп қойылысында оның шешімін табу керектігі айтылған. Бірақ ол есеп
шығарушының ойына бағыт беріп тұрған жоқ. Сондықтан талаптан бұрын
теңдеудің жүйеге жіктелуін жазып қоялық.

Жүйенің екінші теңдеуі екінші дәрежелі үшмүшелік. Осы ақпар есеп
шығарушының ойын теңдіктің екі жағында х2 бөлуге бағыттайды. Сонда

Жүйедегі ақпар бойынша құрылымы тұрақты f(х) функциясы үшін дәреженің
негізін алатындығымыз анықталды. Бірақ (1) теңдеудің оң жағындағы функцияны
түрлендіріп жүйедегі квадрат теңдеуді шығарып алу мүмкіншілігі жоқ.
Сондықтан бірден х2 –қа бөлуден бұрын алдымен берілген теңдеуден ұқсас
өрнектер шығарып алу керектігі айтылып тұр. Басқаша айтқанда, берілген
теңдеуді алдымен ұқсастандыру процесіне теңдеуді жүйеге келтіруіне дейін
бағыттап тұр. Осы ақпарды іске асыратын жолдар төменде көрсетілді.
(х2 + х + 1)2 ( х2(2х2 + х2 + х + 1) ( (х2 + х + 1)2 ( 2х4 + х2(х2 + х + 1)
(

Екінші мүшедегі өрнекті у – пен белгілесек, онда келесі жүйені аламыз
және оны түрлендіру арқылы кері амалдар әдісімен шешілетін жүйе де алынды.

Сонымен берілген теңдеудегі мүшелерді ұқсастандыру арқылы теңдеуді
жіктеп жүйеге келтіруге болатындығы шешілді.
3 –есеп.
3 –есепте құрылымы тұрақты функция берілді де квадрат үшмүше- ліктің
кооффициенттерін анықтау мәселесі жүйеде көрсетілген. Егер у –ті екінші
дәрежеге шығарсақ, онда

аламыз. Бірақ бұл теңдеудің оң жағындағы өрнектен өзгеше. Осы салыстыру
процесінің нәтижесінде қабылдайтын шешім - теңдіктің екі жағында 2 –ге
бөлу. Сонда

(2) теңдіктің оң жағында тұрған өрнекпен 3 –есептің оң жағындағы өрнек
құрылымын салыстырып олардың екі мүшелерінің бірдейлігі анықталады. Мына
нөлді қоссақ, онда айырмашылық жойылады. Теңдеуді шешу мүмкіншілігін
туғызатын келесі жүйелерді аламыз:

Құрылымында тұрақты функция берілмеген бөлшек теңдеуді қарастырайық.

4 –есептің құрылымынан бірден квадрат үшмүшелік табылатыны көрінбейді.
Бір бүтін көпмүшелігі бар теңдеу шығады деген оймен жүйеге Ф(у) ( к теңдеуі
жазылды. Содан кейін ол теңдеуден квадрат үшмүшелігі бар теңдеудің
құрылымын қалай анықтауға болатынын білу үшін Ф(у)(к жалпыланған теңдеуін
квадрат теңдеу түрінде жазылды. Әзірше теңдеу құрылымынан ештеме
байқалмайды. Бірақ, тәуелсіз айнымалы х-тер бірыңғай орналасса, онда тиісті
шешім қабылдайтын ақпар пайда болар деген ой бөлшектерді х –ке бөлуге
бағыттайды. Осы ойымызды орындағанда мына теңдеуді аламыз.

Бөлшек бөлімінде құрылымы тұрақты функция пайда болды. Соны пен
алмастырсақ, онда берілген теңдеудің дәреже көрсеткіші төмендетілетіндігі
мына теңдеулер жүйесінен байқалады.

Қарастырылған теңдеулердің түрлендіру процестерін зерттеп мынадай
әдістемелік қортындыға келдік.
1. Күрделі теңдеудің барлығы квадрат теңдеудің құрылымына басқа
функция енгізу арқылы құрастырылған. Теңдеуге енгізілген функцияның
құрылымы өзгеріп тұрады. Бірақ ол функцияның құрылымын анықтамай және оны
теңдеу құрылымынан ажыратып алмай теңдеу шешілмейді. Күрделі теңдеуді шешу
процесі бірнеше кезеңге бөлінеді. Бірінші кезеңі үшін осы жүйе алынып
студенттердің ойын осында кездесетін нақтыны жалпылау процестері арқылы
абстракциялық ойларын қалыптастыру көзделіп отыр.
2. Теңдеулерді қалай болса-солай бермей оны студенттердің білім
деңгейін дамытуға сәйкестендіріп, түрлендіру процесін біртіндеп реттеп
берудің пайдасы барлығын 2 –ші теңдеуден аңғаруға болады. Шынында да,
алдыңғы теңдеуді х2 –қа бөлу арқылы ықшамдалып шешілді. 1 –мен 2 –ші
теңдеулердің құрылымының ұқсастығынан шешу әдістері де бірдей болады деген
ой пайда болды. Студентті пайда болған проблемамен бетпе-бет кездестіру
міндет. Содан кейін проблеманың шешімін ғылыми тұрғыдан түсіндірсе, онда
келесіде студент ой инертциясына жол бермеуге тырысады, яғни х2 + х + 1
және 3х2 + х + 1 ұқсастандыру тұрғысынан қарастыру керектігін түсініп есіне
сақтауға тырысады.
3. Әрбір кезеңде түрлендіру процестеріне қатысты орындалатын амалдар
саны аз. Түсіну проблемасыда бөлшектеніп бір –біріне жалға- сып, реттеліп
ой үздіксіз қозғалысқа келеді.
4. Оқулықтарда және әдістемелік әдебиеттерде үлгі есеп немесе
есептің кілті деп құрылымы нақты теңдеулердің есептемесін береді. Бірақ
олар оған қосақталған жаттығу есептерінің ойлау жүйесін басқара алмайды.

Осының себебін анықтап, тиісті қорытынды жасалық. Үлгі есеп пен
есептің кілті нақты теңдеу арқылы түсіндіріледі. Жаттығу есептерінде де
құрылымы өзгертілген нақты теңдеулер. Олардың есептемелері үлгі
есептемелерінен өзгеше. Осы кезде интерференциялық құбылыс пайда болады.
Оқыту саласындағы интерференциялық құбылыстың мағынасын былай түсіндіруге
болады. Мағына жағынан бір –бірімен байланысы жоқ он –онбес сөздердің
тізімін оқушыларға оқып шыққаннан кейін олардан сол тізімдегі сөздерді
қайталап беру талап етілсе, олар қайталап бере алмайды. Себебі әрбір
сөздегі мағыналар бірін –бірі өшірді. Интерференциялық құбылыстан құтылу
жолы бар ма? – деген сауал туындайды. Жаттығу есептеріндегі күрделі
теңдеулерді логикалық –функциялық негізде ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.