Анықтауышты жол немесе баған бойынша жіктеу

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:

Алгебралық толықтауыштар және минорлар. Анықтауышты жолдың не бағанның элементтері бойынша жіктеу.

1-анықтама. Үшінші ретті анықтауыштың (11) өрнегіндегі (3-п. ) а _ij элементін қамтитын мүшелерін бір бөлек топтап, жақша сыртына а _ij элементін шығар

ғаннан кейін жақша ішінде қалатын өрнекті а элементінің алгебралық толықтауышы деп атайды және оны А арқылы белгілейді.

Мысалы, (11) өрнекте а ₂ элементін қамтитын мүшелер а ₁₂ а ₂₃ а ₃₂ және (-а _и а ₂₃ а ₃₂ ) . Сондықтан,

А ₂₃ =а ₁₂ а ₃₁ - а ₁₁ а ₃₂

2-анықпгама. Үшінші ретті анықтауыштыш а _ij элементінің миноры М _i j деп берілген анықтауыштың і-інші жолын және ] '-інші бағанын сызып тастағанда шығатын екінші ретті анықтауышты айтады .

Мысалы,

М = =а ₁₁ а ₃₂ -а ₁₂ а ₃₁

Жоғарыдағы А ₂₃ пен М ₂₃ мәндерін салыстырып, А ₂₃ = -М ₂₃ болатындығын байқаймыз.

Жалпы алғанда қайсыбір элементтің алгебралық толықтауышы сол элемент тұрған жол мен бағанның нөмірлерінің қосындысы жұп болғанда плюс таңбамен алынған, ал бұл қосынды тақ болғанда минус таңбамен алынған сол элементтің минорына тең болатынын тексеруге болады, яғни

А _ij =(-1) ^I+j М _ij . (13)

Теорема. Анықтауыштьщ қайсыбір жолының (бағанның) элементтерінің өздеріне сәйкес алгебралық толықтауыштар мен көбейтінділерінің қосындысы анықтауыш шамасына тең болады.

Анықтауыштың бір жолының (бағанның) элементтерінің басқаша жолдың (бағанның) сэйкес элементтерінің алгебралық толықтауыштары мен көбейтінділерінің қосындысы нолъге тең болады.

Анықтауыштың әрбір қосылғышы әр жолдан және әр бағаннан көбейткіш ретінде бір-бір элементтен ғана қамтиды. Сондықтан анықтауыштың 1-анықтамасын және алгебралық толықтауыштың 1-анықтамасын ескере отырып, мына теңдіктерді шығарып алу оңай:

=а ₁₁ А ₁₁ +а ₁₂ А ₁₂ +а ₁₃ А ₁₃

=а ₂₁ А ₂₁ +а ₂₂ А ₂₂ +а ₂₃ А ₂₃ (14)

=а ₃₁ А ₃₁ +а ₃₂ А ₃₂ +а ₃₃ А ₃₃

Анықтама кез келген ретті анықтауыштар үшін де тура болады.

= а ₁₁ А ₁₁ +а ₂₁ А ₂₁ +а ₃₁ А ₃₁

= а ₁₂ А ₁₂ +а ₂₂ А ₂₂ +а ₃₂ А ₃₂ (15)

= а ₁₃ А ₁₃ +а ₂₃ А ₂₃ +а ₃₃ А ₃₃

(14) теңдіктер анықтауыштың сәйкес түрде бірінші, екінші және үшінші жолдарының элементтері бойынша жіктелулері де, ал (15) теңдіктер - бірінші, екінші және үшінші бағандардың элементтері бойынша жіктелулері деп аталады. Бұл теңдіктер теореманың бірінші бөлімін дәлелдейді де,

енді екінші бөлімін дәлелдейік. Мысалы, бірінші жолдың элементтерінің үшінші жолдың сәйкес элементтерінің алгебралық толықтауыштарына көбейтінділерінің қосындысы нольге тең болатындығын көрсетейік. Ол үшін (14) теңдіктердің үшіншісін алайық. Алгебралық А ₃₁ А ₃₂ А ₃₃ толықтауыштар а ₃₁ а ₃₂ , а ₃₃ элементтерінің өздеріне тәуелді емес, сондықтан оларды кез келген к ₁ к ₂ к ₃ сандарымен ауыстырсақ, мынау шығады

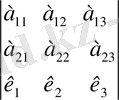= к ₁ А ₃₁ +к ₂ А ₃₂ +к ₃ А ₃₃

Егер осы теңдікте к ₁ =а ₁₁ к ₂ =а ₁₂ к ₃ =а ₁₃ деп алсақ, оның сол жағында тұрған анықтауыш нольге тең болады (оның бірінші және үшінші жолдары бірдей) . Сондықтан

А ₁₁ А ₃₁ +а ₁₂ А ₃₂ +А ₁₃ А ₃₃ =0

Басқа жағдайлар да осыған ұқсас түрде тексеріледі.

Қарастырылып отырған жолдың немесе бағанның бір элементінен өзгелері нольдер болып келген жағдайда (14) не (15) формулаларды қолдану аса тиімді, өйткені бұл жағдайда жіктелуде бір ғана қосылғыш қалады және анықтауыштың рет саны бір бірлік кемиді. Егер жолдарда немесе бағандарда нольдер болмаса, онда алдымен 8) қасиетті пайдаланып кез келген жолдың не бағанның бір элементінен өзгесін нөльге айналдырып алып, содан кейін (14) не (15) формулалардың бірін қолдану керек.

Мысал. Мына анықтауышты есептеу керек.

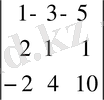
Бірінші жолда нольдер шығарайық. Ол үшін бірінші бағанды алдымен 3-ке, содан кейін 5-ке көбейтіп, нәтижелерін сәйкес түрде екінші және үшінші бағандарға қосамыз. Сонда 8) қасиет бойынша мына теңдік шығады

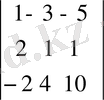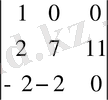
Бұдан кейін анықтауышты бірінші жолдың немесе үшінші бағанның (онда да екі нөль шықты) элементтері бойынша жіктеуге болады. Үшінші бағанның элементтері бойынша жіктесек, мынау шығады

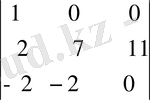=11*(-1) ²⁺³ 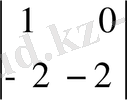=-11(1*(-2) -0*(-2) ) =22

Ендеше

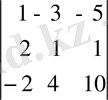= 22.

Анықтауышты жол немесе баған бойынша жіктеу

Біз үшінші ретті анықтауышты есептей білеміз. Ал реті үштен жоғары болған жағдайда жолдың немесе бағанның элементтері бойынша жіктеп ретін төмендетуге болады. Төртінші ретті анықтауыш берілсін :

= (17)