Жиындардың алгебрасы мен σ-алгебра: өлшенетін кеңістік және оқиғалар алгебрасы


Қазақстан Республикасының Білім және ғылым министрлігі
Ы. Алтынсарин атындағы Арқалық мемлекеттік педагогикалық институты
Жаратылыстану және ақпараттандыру факультеті
Математика, физика, информатика кафедрасы.
Тақырыбы:
Алгебра және жиындарының
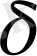 - алгебра.
- алгебра.
Орындаған: И - 31 тобының студенті
Абдибаева Г.
Тексерген: Төлегенова А
Арқалық - 2008.
Жоспар:
І. Кіріспе.
ІІ. Негізгі бөлім
1) .
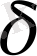 - алгебра. Өлшенетін кеңістік.
- алгебра. Өлшенетін кеңістік.
2) . Жиындардың алгебрасы және
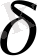 - алгебралары.
- алгебралары.
3) . Оқиғалар. Оқиғалар алгебрасы.
ІІІ. Қорытынды бөлім.
Пайдаланылған әдебиеттер.
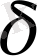 - алгебра. Өлшенетін кеңістік.
- алгебра. Өлшенетін кеңістік.
Ықтималдықтар теориясы математика ғылымының бір саласы болғандықтан оны формалды - логикалық негізінде құру мәселесі келіп шығады. Аксиоматикалық методка ықтималдықтар теориясын құруды алғаш негіздеген совет математигі С. Н. Бернштейн (1880 - 1968) .
Бірақ бұл саланың толық аксиоматикалық жүйесін берген әйгілі совет математигі академик А. Н. Колмогоров.
Ықтималдықтың классикалық кездейсоқ оқиға бастапқы ұғымға жататын.
Колмогоров аксиоматикасында кездейсоқ оқиға бастапқы ұғым емес, ол басқа элементар ұғымдар негізінде жасалады.
Мысал, нүктені [t 1 , t 2 ] кесіндісіне кездейсоқ лақтырудың континуум нәтижесі болады, өйткені нәтижесі осы кесіндідегі кез келген нүкте болуы мүмкін. Бұл кесіндіге, мәселен, осы аралықтағы температураның өзгеруі, уақыттың өзгеруі т. т жатады.
Нәтижесі шекті я саналымды шексіз жиын болғанда сынаудың әрқандай нәтижесінің жинағы оқиға болатын болса, қарастырып, отырған бұл мысалда мәселе басқаша. Өйткені бұл кесіндінің қалаған ішкі оқиға десек онда көптеген қиындыққа кезедесеміз.
Сондықтан мұндай жағдайда оқиға болу үшін арнайы ішкі жиындар класын құрудың қажетілігі туады. Енді элементтері оқиға болатын сондай жиындар класын құрайық.
Элементар оқиғалар кеңістігі
 болсын. Мұның ішкі жиындар системасын
Ғ
болсын. Сонда оқиғалар алгебрасы болу үшін мынав аксиомалар /шарттар/ орындалатыны айтылғанды. Олар:
болсын. Мұның ішкі жиындар системасын
Ғ
болсын. Сонда оқиғалар алгебрасы болу үшін мынав аксиомалар /шарттар/ орындалатыны айтылғанды. Олар:
- Элементар оқиғалар кеңістігі- ның өзі Ғ жиынында элемент ретінде
жатады, яғни

- Егер де А оқиғасы және В оқиғасы элемент ретінде Ғ системасында
жатса, онда бұл системада олардың бірігуі де, қиылысуы да жатады, яғни
 және
және
 - тан
- тан
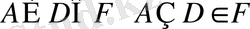 шығады.
шығады.
- Егер де А оқиғасы элемент ретінде Ғ системасында жатса, онда оған
қарама - қарсы
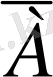 оқиғасы да сол Ғ системада жатады, яғни
оқиғасы да сол Ғ системада жатады, яғни
 болса онда
болса онда
 .
.
Әрине
 , өйткені
, өйткені
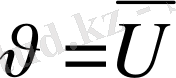 .
.
2 мен 3 қасиетті бірігу, қиылысу және толықтыру операцияларының орындалуы деп ұғылады.
Біз оқиғалар саны шекті болғанда мысалы екеу болғанда Ғ системасының қалайша жасалуын қарастырдық /
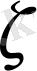 І - ді қара /. Ал егерде оқиғалар саны шексіз болса, онда Колмогоров аксиоматикасында тағы да бір талап қойылады.
І - ді қара /. Ал егерде оқиғалар саны шексіз болса, онда Колмогоров аксиоматикасында тағы да бір талап қойылады.
4 аксиома 2 - шінің кеңейтілген түрі Ғ системасында А
1
, А
2
. . . А
п
тізбектер жиыны жатса, онда оған олардың бірігуі мен қиылысуы да жатады, яғни
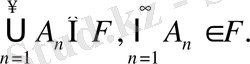
Ескерту: 2 - ші және 4 - ші аксиомалардан қорытады бір мәселе ол бірігу я қиылысу операцияларының біріне толықтыру операциясын қолданса, одан екінші операция шығады. Шынында,
 болғанда
болғанда
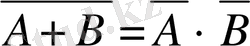 .
.
Сонымен оқиғалар алгебрасы деп бірігу, қиылысу және толықтыру операциялары шекті сан рет орындалған және бұларға қарағанда жабық жиындар класын жасайтын алгебралар системасында айтқан болатынбыз.
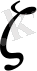 - ді қара. Бұл операциялар саналымды шексіз орындалғанда жабық жиындар класын жасаса, онда мұндай жиындар класы Ғ системасын
- ді қара. Бұл операциялар саналымды шексіз орындалғанда жабық жиындар класын жасаса, онда мұндай жиындар класы Ғ системасын

 -алгебра немесе оқиғалардың борельдік өрісі немесе оқиғалар өрісі деп атайды. Ғ система элементтері оқиға болады. Бұдан былай
-алгебра немесе оқиғалардың борельдік өрісі немесе оқиғалар өрісі деп атайды. Ғ система элементтері оқиға болады. Бұдан былай
 жиыны мен
жиыны мен
 -алгебра құруға Ғ системасы берілсе, өлшенетін кеңістік берілген дейміз, сөйтіп мұны
-алгебра құруға Ғ системасы берілсе, өлшенетін кеңістік берілген дейміз, сөйтіп мұны
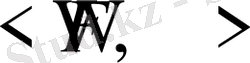 пен белгілейміз. Сонымен қандай да ықтималдықтар есебін формалдау қажетттіг туатын болса, онда оны (экспериментті) өлшенетін кеңістікке, яғни
пен белгілейміз. Сонымен қандай да ықтималдықтар есебін формалдау қажетттіг туатын болса, онда оны (экспериментті) өлшенетін кеңістікке, яғни
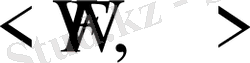 -ге сәйкестендіру керек.
-ге сәйкестендіру керек.
Айтылғандарды мынадай бір мысалмен түсіндірейік.
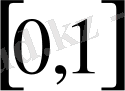 кесінді нүктелері континиум. Бұл кесіндіні шекті кесінді я интервалдарға бөліп жиын (система) жасасақ, онда бұл система оқиғалара алгебрасын құрайды, бірақ жасамайды.
кесінді нүктелері континиум. Бұл кесіндіні шекті кесінді я интервалдарға бөліп жиын (система) жасасақ, онда бұл система оқиғалара алгебрасын құрайды, бірақ жасамайды.
Ал егер бұл кесіндінің барлық ішкі жинағын алсақ ол
 -алгебра жасайды. Әрине, Ғ системасында жатпаған
-алгебра жасайды. Әрине, Ғ системасында жатпаған
 жиынның қалған барлық ішкі жиындары оқиға болмайды.
жиынның қалған барлық ішкі жиындары оқиға болмайды.
Сонымен,
 -ны ақиқат оқиға дейміз. 1, 3 аксиома бойынша бос жиын
-ны ақиқат оқиға дейміз. 1, 3 аксиома бойынша бос жиын
 - ны мүмкін емес, оқиға дейді.
- ны мүмкін емес, оқиға дейді.
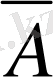 - ны Ф - ға қарама - қарсы немесе А - ны толықтаушы оқиға дейді.
- ны Ф - ға қарама - қарсы немесе А - ны толықтаушы оқиға дейді.
Жиындардың алгебрасы және
- алгебралары.
Нәтижелері саналмайтын тәжірибенің ықтималдық моделін
жасап шығу көптеген қиындықтармен ұштасып жатыр, бұл геометриялық ықтималдықтарға келтірілген мысалдардан - ақ көрініп тұр. Мұндай қиыншылықтар қазіргі кезде ықтималдықтар теориясының аксиомалар системасы негізінде толық шешілген. Бұл мәселелерді түсіну мақсатында өлшемдер теориясынан ақпар берелік.
Қайсы бір тиянақты Е жиынын және оның ішкі жиындарын қарастырамыз. Ішкі жиындардың жиынын класс деп атауға болады.
Анықтама: Е - ден алвынған ішкі жиындапрдың К класын мына шарттар орындалғанда алгебра деп аталады.
- Е жиынын К класының элементі болады, яғни;
- А жиынын К класының элементі болса, онда А толықтауыш жиыны
да К - ның элементі болады, яғни


- егержәнеболса, онда.
Анықтама. Е - ден алынған ішкі жиындардың Ғ класын мына шарттар
орындалғанда
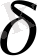 -
алгебра деп атайды:
-
алгебра деп атайды:
1.

2. егер
болса, онда

3. егер
болса, онда
.
Сөйтіп,
- алгебрада шексіз қосылғыштардың қосындысы, ал
алгебрада екі жиынның қосындысы жатады.
Теорема. Кез келген К жиындардың класы үшін осы К класын енгізетін ең кіші
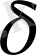 (К) алгебрасы табылады.
(К) алгебрасы табылады.
Бұл теоремадағы «ең кіші
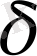 -
алгебра » дегенді былай түсіну керек:
-
алгебра » дегенді былай түсіну керек:
1.
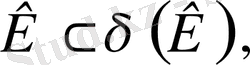
2. қандай да болмасын
 болатындай Ғ
болатындай Ғ
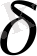 -
алгебрасы үшін
-
алгебрасы үшін
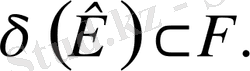
Дәлеледеу: К класын өзіне енгізетін кем дегенде бір
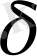 -
алгебра бар. Мұндай
-
алгебра бар. Мұндай
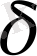 -
алгебра, мысалы, Е жиынының ішкі жиындарының жиыны.
-
алгебра, мысалы, Е жиынының ішкі жиындарының жиыны.
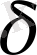 (К) арқылы К класы жатаны барлық
(К) арқылы К класы жатаны барлық
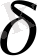 -
алгебралардың көбейтіндісін белгілейік. Сонда
-
алгебралардың көбейтіндісін белгілейік. Сонда
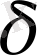 (К)
(К)
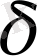 -
алгебра болады. Шынында да, кез келген санды
-
алгебра болады. Шынында да, кез келген санды
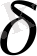 -
алгебралардың көбейтіндісі
-
алгебралардың көбейтіндісі
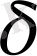 -
алгебра болатындығын тексеру қиын емес. Ал егер, Ғ
-
алгебра болатындығын тексеру қиын емес. Ал егер, Ғ
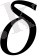 -
алгебрасы К класын өзінде жатқызса, онда
-
алгебрасы К класын өзінде жатқызса, онда
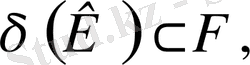 яғни
яғни
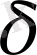 (К)
(К)
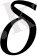 -
алгебра.
-
алгебра.
Оқиғалар. Оқиғалар алгебрасы.
Комплексті шарт, сынау, оқиға. Бұл ұғымдарды түсіндіруді мысалдардан басатйық.
1 - мысал. Теңгені (металл ақшаны) теп - тегіс еденге лақтырайық, сонда мына төмендегі құбылыстарды байқаймыз. Теңгені лақтыру үшін өзімізді, белгілі бір қалыпқа келтіреміз. Одан соң бас бармақпен теңгенің бір ұшын жоғары қарай түртіп жібереміз. Сонда ол шыр көбелек ацйналып, белгілі бір биіктікке дейін көтеріліп, төмен қарай құлдилап, еденге түседі де бірнеше рет серіктеп, жалпыланған не тиын жағы, не герб жағы жоғарғы қарап жатады. Сайып келегенде, теңге жалпағынан жатуы үшін көптеген қимыл әрекеттер жасалады, солардың жиыны комплексті шарт деп аталады. Оның тиын (не герб) жағының жоғарғы түсуі (жатуы) - осыф комплесті шарттың орындалу нәтижесі - оқиға деп аталады.
Комплекті шарт термині орнына сынау, тәжірибе, эксперимент терминдерін де пайдаланылады. Біз көбінесе сынау терминін қолданамыз. Бұдан былай сынау нәтижесін оқиға деп ұғамыз. Әдетте оқиғаларды үлкен әріптер А, В, С, . . . арқылы, ал бұларға қарама - қарсы оқиғаларды
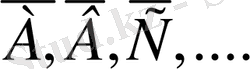 арқылы белгілейміз. Мысалы, теңгенің тиын жағының пайда болуы А оқиғасы болса, герб жағынгың пайда болуы
арқылы белгілейміз. Мысалы, теңгенің тиын жағының пайда болуы А оқиғасы болса, герб жағынгың пайда болуы
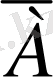 оқиғасымен белгіленді және т. с. с.
оқиғасымен белгіленді және т. с. с.
Оқиғаларды класқа бөлу. Сынау жүргізілгенде А оқиғасы пайда болуы да, пайда болмауы да мүмкін болса, ондай оқиғаны кездейсоқ оқиға деп атайды. Мұндай оқиғаларда 1, 2 мысал жатады. өйткені сынау нәтижесінде теңгенің (кубтың) белгіленген жағының пайда боларын күн ілгері айта алмаймыз. Сынау нәтижесінде оқиға (а оқиғасы) сөзсіз пайда болатын болса, ондай оқиғаны ақиқат оқиға дейді. Сынау нәтижесінде оқиғаның (А оқиғасы) пайда болуы мүмкін болмаса, ондай оқиғаны мүмкін емес оқиға дейді.
Ақиқат оқиғаны
 әрпімен, мүмкін емес оқиғаны V әрпімен белгілеу қабылданған. Мысалы, қобдишаға салынғапн ақ шарлардың біреуін алсақ, оның ақ болып шығуы ақиқат оқиға да, басқа түсте болуы мүмкін емес, оқиға. Сынау жүргізгенде екі оқиғаның бірі пайда болып, екіншісі пайда болмайтын оқиғаларды үйлесімсіз оқиғалар дейді. Мәселен 2 - мысалдағы А
1
, А
2
(бірінші және екінші нөмерлі жақтар) оқиғалары - үйлесімсіз оқиғалар. Кез келген екі оқиғасы үйлесімсіз болатын оқиғалар жиынын қос - қостан үйлесімсіз оқиғалар дейді.
әрпімен, мүмкін емес оқиғаны V әрпімен белгілеу қабылданған. Мысалы, қобдишаға салынғапн ақ шарлардың біреуін алсақ, оның ақ болып шығуы ақиқат оқиға да, басқа түсте болуы мүмкін емес, оқиға. Сынау жүргізгенде екі оқиғаның бірі пайда болып, екіншісі пайда болмайтын оқиғаларды үйлесімсіз оқиғалар дейді. Мәселен 2 - мысалдағы А
1
, А
2
(бірінші және екінші нөмерлі жақтар) оқиғалары - үйлесімсіз оқиғалар. Кез келген екі оқиғасы үйлесімсіз болатын оқиғалар жиынын қос - қостан үйлесімсіз оқиғалар дейді.
Сынау жүргізілгенде оқиғаның бірінің пайда болуы екіншісінің пайда болуын жоққа шығармайтындай екі оқиғаны үйлесімді оқиғалар деп атайды. Мысалы, кубтың жұп нөмерініңс пайда болуы (А оқиғасы) мен үш санына еселік нөмір пайда болуы В оқиғасы үйлесімді. Өйткені кубтың 6 - нөмерінің пайда болуын көрсететін А 6 оқиғасы О В оқиғасы пайда болғанда да, А оқиғасы пайда болғанда да пайда болуы мүмкін.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz