Тетраэдрға сырттай сызылған сфералық радиусын векторлық әдісті пайдаланып табу

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 4 бет
Таңдаулыға:

Тетраэдрға сырттай сызылған сфералық радиусын векторлық әдісті пайдаланып табу.

Жоғары сыныптарда стереометрияны оқытуға бөлінген уақыттың оқушылардың кеңістікті елестете алу қабілеттерін дамыту үшін кейде тіпті олардың қарапайым есептепді шығаруына мүмкіндік бермейтіндей пән мұғалімдеріне де, әдіскерлерге де белгілі. Мұндай жағдайларда есептерді таза геометриялық жолмен шешу жеңіл болмайтын қиындықтарға душар етеді.

Көрсетілген проблеманы жолдың мүмкін жолдарының бірі - ондай есептеді шешудің векторлық алгебраның аппаратына негізделген тиімді әдістемесіне оқушыларды баулу және үйрету болып табылады.

Көпшілік стереометриялық есептерді шешу негізінен екі түрлі шамаларды, атап айтқанда, арақашықтықтар мен бұрыштарды есептеуге келтіріледі.

Нүктеден түзуге дейінгі және нүктеден жазықтыққа дейінгі арақашықтықты, айқас түзулердің арасындағы арақашықтықты және бұрышты табуға берілген есептерді векторлардың қасиеттеріне негізделген стандартты алгорифмдерді пайдалану арқылы шешу әлдеқайда жнңіл және өте тиімді.

Сондай-ақ векторлық әдісті оқушылар үшін қиындығы барынша жоғары деп саналып келінген және солай деп саналатын сфера мен көпжақтардың комбинацияларына байланысты болып келген есептерді де шешуге пайдалану барынша тиімді болып табылады.

Сондықтан да есептердің жоғарыда атап көрсетілген типтеріне векторлық әдісті пайдаланып шығаруға оқушыларды баулу мәселесі, бүгінгі таңда математиканы оқытудың теориясы мен әдістемесі саласындағы өзекті мәселелердің бірі болып табылады.

Бұл мақалада вектролық әдісті пайдаланып, берілген тетраэдрға сырттай сызылған сфераның радиусын табу мәселесіне тоқталайық.

Келесі есепті қарастырайық. Айталық, NABC тетраэдры берілсін, ал О нүктесі оған сырттай сызылған сфераның центрі болсын. Тетраэдрдың қабырғасы бір төбесінен шығатын үш қырының ұзындықтары және бұл қырлардың араларындағы жазық бұрыштардың косинустары бізге берілген болсын, не оларды есептің шартында берілген мәліметтер бойынша есептеп табу мүмкін болсын деп есептейік. Осы жағдайда тетраэдрға сырттай сызылған сфераның радмусын табу талап етілсін. Егер тетраэдр атап көрсетілгендей шарттармен берілген болса, онда қойылған есепті шешудің тиімді әдістемесін жасауға болады. Бұл әдістеме векторлық әдісті, яғни векторлық алгебраның аппаратын пайдалануға негізделген. Енді осы әдістеме бойынша жоғарыда қойылған есепті шешу мәселесіне көшеміз.

Айталық, мысалы, N төбесінен шыққан NA, NB, NC қырларының ұзындықтары және BNC, ANC, ANB жазық бұрыштарының шамалары белгілі болсын. Базистік векторлар ретінде NA=p, NB = q, NC = r

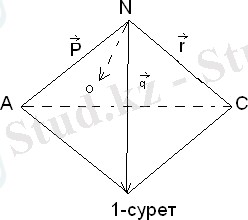векторларын таңдап аламыз.

Бұл жағдайда базистік вектроларды көбейту кестесі толық анықталады.

Айталық, NO = ХP + yq + Zr болсын, онда OA = P - NO, OB = q - NO, OC = r - NO теңдіктері орындалады.

Бұған қосымша

NO ² = OA ² = OB ² - OC ² = R ²

Теңдіктерінің орынды болатындығы түсінікті, мұндағы R - тетраэдрға сырттай сызылған сфераның радиусы.

(Ә) теңтіктерден келесі теңдіктер келіп шығады.

(NO-OA) (NO+OA) =O ₁

(NO-OB) (NO+OB) =O ₁ (3)

(NO-OC) (NO+OC) -O

теңдіктерді және NO+OA=p, NO+OB=q, NO+OC=r теңдіктерін ескерсек, онда (3) келесі түрге келеді.

(2NO-p) p = O ₁ (2 NO - q ) q = O ₁ (2 NO - r ) r = O

p NO = 1/2

(А) - х, y және Z белгісіздеріне қатысты үш сызықты теңдеулер жүйесі болып табылады. Осы жүйеден базистік векторларды көбейтудің белгілі кестесі арқылы х, y және Z шамаларын анықтап алып, NO векторының базистік векторлар бойынша жіктелуін табамыз. Бұдан әрі R=NO=NO ² формуласын пайдаланып, NABC тетраэдроны сырттай сызылған сфераның радиусын табамыз.

1-есеп. NABC пирамидасының табаны қабырғасының ұзындығы 5-ке тең теңқабырғаны ABC үшбұрышы. Сонымен бірге AN=BN=41 CN = екендігі белгінің NABC пирамидасына сырттай сызылған радиусын табыңдар.

Шешуі: Алдымен ANB, ANC және BNC үшбұрыштарына косинустар теоремасының салдарын қолдану арқылы N төбесіндегі ANB, ANC және BNC жазық бұрыштардың косинустарын табамыз.

(А сурет) .

Базистік векторлар ретінде NA=p, NB=q, NC=r векторларын таңдап алып, базистік векторларды көбейту кестесін құрстырамыз:

: p

p: 16

q: 7/2

r: -27/8

: q

p: 7/2

q: 16

r: -27/8

: r

p: -27/8

q: -27/8

r: 9/4

Айталық, О нүктесі NABC пирамидасына сырттай сызылған сфераның центрі, ал R осы сфераның радиусы және NO=хp+yq+zp болсын, сонда (А) жүйе біздің жағдайымызда мынадай түрге келеді.

p(хp+yq+zr) =8 ₁

q(хp+yq+2r) =8 ₁

r(хp+yq+zr) =

бұдан

Олай болса

Базистік векторларда қарастырылып отырған тетраэдрдың қырларымен байланысты етіп таңдап алу міндетті емес. Мұндай жағдайда есепті шығарудың әдістемесі ешқандай өзгеріссіз қалады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.