Электромагниттік толқындардың табиғаты, қасиеттері және қолданылу салалары


Мазмұны
КІРІСПЕ . . . 3
1 ЭЛЕКТРОМАГНИТТІК ТОЛҚЫНДАРДЫҢ ТАБИҒАТЫ
1. 1 Электромагниттік толқындардың табиғаты және қасиеттері . . . 5
1. 2 Электромагниттік толқынның энергиясы . . . 37
1. 3 Электромагниттік толқындарды алу . . . 39
2 ЭЛЕКТРОМАГНИТТІК ТОЛҚЫНДАРДЫ ҚОЛДАНУ
2. 1 Электромагниттік толқындарды әр түрлі салада қолдану . . . 57
2. 2 Электромагниттік толқындардарды ақпараттандыру жүйесінде
қолдану . . . 68
2. 3 Электромагнитті толқындарды ғарыш әлемін зерттеуде
қолдану . . . 74
ҚОРЫТЫНДЫ . . . 78
ӘДЕБИЕТТЕР . . . 80
Кіріспе
Қазақстан - 2030 ұзақ мерзімді басылымдылығына байланысты машина, кеме, авиация, әуе зымыранын жасау және техниканың басқа да салаларын дамыту - негізгі мәселелердің бірі болып табылады. Ал жаратылыстану ғылымдарының ішінде физика қазіргі уақытта табиғат танудағы негізгі ғылымдардың бірі болып табылады. Ол ғылымның, техниканың және өндірістің әр түрлі салаларын дамытуда зор ықпалын тигізіп отыр. Соның бір бағыты электромагниттік толқындардың қолданылуы. Электромагнитті толқындар материяның өмір сүруінің ерекше түрі болып табылады. Электромагнитті толқындар екі жақты қасиеттерге ие. Бірі оның бөлшек “фотон” түрінде таралуы, екіншісі толқын түрінде таралуы. Бұл бір - біріне қарам - қарсы екі жақты ұғымның бірге бір құбылыстың бойында болуы табиғат құбылыстарының тұтастығын көрсетеді және материяның өмір сүру формасының көп түрлілігін дәлелдейді. Бұл оқушылардың табиғат құбылыстарына деген толық және терең ғылыми көзқарасын қалыптастыруға мүмкіндік беруі. Электромагниттік толқындардың көзі тербелмелі контурдағы электр құбылыстары болып табылады. Контур көбірек энергия шығару үшін ондағы конденсаторларды бір - бірінен алыстатуымыз қажет. Контур 180° градусқа қарай орналасқан кезде жоғары электромагниттік толқын аламыз. Осылайша алынған толқын кеңістікте электромагниттік толқын ретінде таралады. Алғаш рет мұндай толқынды 1888 ж. Г. Герц алды. Герцтің алған толқыны өшетін болды. Ол аралық жарқырайтын вибратор шығаратын толқын болды. Мұндай вибраторлар электромагниттік толқынның барлық спектрін қамтыды.
Тақырыптың өзектілігі электромагнитті толқындардың негізгі қасиеттерін, қазіргі таңдағы қолданылу шеңберін зерттеу. Электромагнитті толқындар деп - электр және магнит өрісітерінің кеңістікте бірін - бірі тудыру нәтижесінде таралуын айтамыз. Электромагниттік толқынның шығарылуы мен жұтылуы техникада, тұрмыста, өмірде кеңінен қолданылады және жылдан-жылға бұл процесс жетілдіріліп отырады. Қарапайым Герц вибраторынан бастап қазіргі интернет байланыс жүйесі осы құбылысқа негізделген.
Ғылыми жаңалығы электромагниттік толқындардың қазіргі уақыттағы қолданылу шеңберін жаңа сала бойынша зерттеу және оны талдау.
Практиканың маңыздылығы электромагниттік толқындарды қолданылу шеңберін зерттеп, оқу үрдісінде қолданылу әдістемесін жетілдіру.
Шешілетін ғылыми мәселелердің қазіргі жағдайы
электромагнитті толқындар спектрінің қолданылу мәселелерін, жетістіктерін талдаумен байланысты. Ақпараттық жүйеде кеңінен қолданылады.
Жұмыстың мақсаты электромагниттік толқындардың қазіргі уақыттағы қолданылу шеңберін зерттеу және айқындау.
Жұмыстың міндеттері
1. Электромагниттік толқындардың табиғатын жүйелеу және оларды алу жолдарын зерттеу.
2. Электромагниттік толқындардың қаситеттерін талқылау.
3. Электромагниттік толқындардың шығарылуы мен жұтылу құбылысын ғылыми теориялық тұрғыдан түсіндіру.
4. Электромагнитті толқындардың әр түрлі салада қолданылуын жүйелеу.
Зерттеу обьектісі
электромагниттік толқындар табиғатын, ерекшеліктерін және қолданылуын зерттеу.
Теориялық негізі электромагниттң толқындар табиғаты мен қасиеттерін көру және қолданылуын зерттеу.
Әдістемелік негізі электормагнитті толқындардың қолданылу бағыттарын алу және әдістемелік нұсқауларын ұсыну.
Практикалық базасы жұмыстың орындалуы мен оған қатысты өткізілген дипломдық тәжірибе Ы. Алтынсарин атындағы Арқалық мемлекеттік педагогикалық институты кітапхана базасында, видиозалда жүргізілді. Сонымен қатар Л. Н. Гумильев атындағы Еуразия Ұлттық Университеті және Әл- Фараби атындағы Қазақ Ұлттық Университетінің кітапханаларының қоры пайдаланылды. Интернет жүйесі бойынша ізденіс жұмыстары жүргізілді.
1. Электромагниттік толқындар туралы жалпы түсінік
1. 1 Электромагниттік толқындардың табиғаты және қасиеттері.
Электромагниттік индукция құбылысын М. Фарадей кез келген магнит өрісінің өзгерісі құйынды электр өрісін туғызатындығымен түсіндірді.
Кез келген электр өрісінің өзгерісі құйынды магнит өрісін тудырады деп Д. К. Максвелл 1864 жылы болжау жасады.
Егер бұл жорамал дұрыс болса, электр және магнит өрістері кезектесіп, бір-бірін тудыру арқасында бір басталған электромагниттік өрісінің өзгеру процесі шектелмей барлық кеңістік бағыттарында жалғасуы тиіс.
Осы кеңістікте айнымалы электр және магниттік өрістерінің таралу процесін электромагниттік толқын деп атайды.
1-суретте өзгеретін электр өрісінің кернеулік Е вектордың бағытын және осы өрістің тудырған құйынды магнит В векторы арасындағы байланыс көрсетілген.
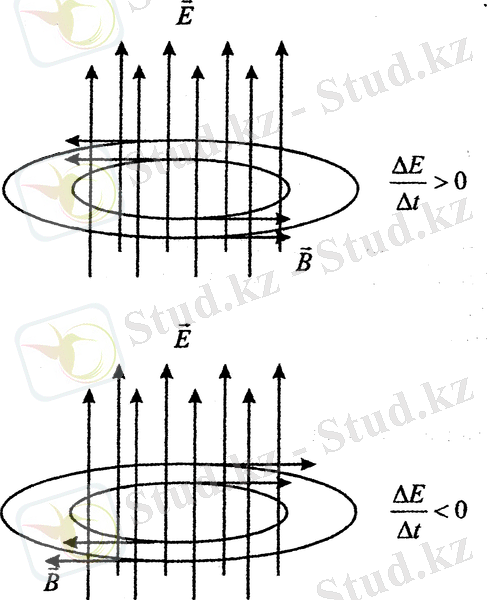
Сурет 1 Өрістердің арасындағы байланыс
Электромагниттік толқынның таралуы үшін ешқандай ортаның қажеті жоқ, электромагнитгік толқынның вакуумда таралу жылдамдығы с-ға тең:
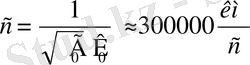 (1. 1)
(1. 1)
Еркін электр зарядтары болғандықтан, өткізгіштердегі электр өрісі әрқашан нөлге тең, сондықтан электромагниттік толқындар өткізгіштік орталарда тарамайды.
Диэлектриктерде электромагнитгік толқындар тарай алады, бірақ олардың таралу жылдамдығы вакуумдағы жылдамдықтан кем болады:
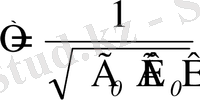 (1. 2)
(1. 2)
мұнда
 және
және
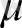 - заттың диэлектрлік және магниттік өтімділіктері.
- заттың диэлектрлік және магниттік өтімділіктері.
Максвелл гипотезасы негізінде есептелген электромагниттік толқынның жылдамдығы тәжірибелерде анықталған жарық жылдамдығына тең болады. Бұл сәйкестік көрінетін жарықты электромагниттік толқындардың бір түрі деген болжам жасалды.
Электромагниттік индукцияны байқау тәжірибелерінде құйынды электр өрісінің магнит ағыны Ф өзгергенде туындайтынын анықтаған болатынбыз. Магнит ағынының өзгерісі осы өрісті тудырған ток күші өзгерісінен болады. Өткізгіштегі ток күшінің өзгерісі электр зарядтарының реттелген жылдамдығы
өзгерісінен, яғни электрондардың үдеуінен пайда болады. Сонымен құйынды электр өрісінің туындауы электрондардың үдемелі қозғалысы есебінен болады. Осы шарт - электромагниттік толқындардың пайда болуының жалпы шарты болып табылады.
Электромагниттік толқындар электр зарядтарының үдемелі қозғалысында туындайды .
Максвеллдің электромагниттік толқындардың болуы туралы гипотезасы физикалық теорияға айналу үшін, бұл гипотезаның негізгі қағидалары тәжірибеде расталуы керек . Максвелл гипотезасы 1887 жылы Генрих Герц өткізген тәжірибелерде толығымен расталып шықты.
2-суретте өзгеретін магнит өрісінің В индукция векторының бағыты және осы өрістің тудырған құйынды электр өрісінің Е векторымен байланысы көрсетілген.
Магниттік индукция векторы В және электр өрісінің кернеулік векторы Е өзара перпендикулярлы және оған қоса бұл екі вектор толқын таралу бағытына перпендикулярлы (2-сурет) .
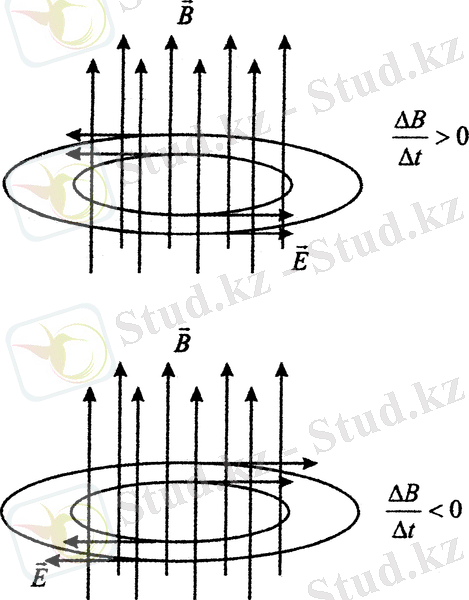
Сурет 2 Толқынның таралу бағыты
Герц тәжірибеге түсінік берген болатын. Тербелмелі контур рөлін атқаратын ұштарында шар бар екі стерженьде разряд процесі барысында электр тербелістері өтеді. Ол кезде электрондар стержень бойымен гармоникалық тербеліс жасайды. Электрондардың үдемелі қозғалысы электромагниттік толқындарды тудырады. Толқын металдық рамкада мәжбүрленген электрлік тербелістерін қоздырады. Егер рамканың тербелмелі контурының өздік тербеліс жиілігі электромагниттік толқынның жиілігіне тең болса, электрлік резонанс байқалады. Контурдағы кернеу жоғары мәнге жеткенде, разряд өтеді.
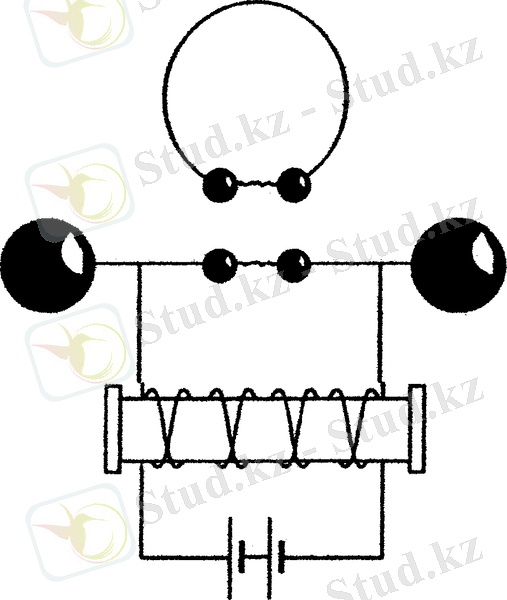
Сурет 3 Контурдағы кернеудің разрядталуы
Контурдағы тербелістің
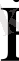 жиілігін және электромагниттік толқынның
жиілігін және электромагниттік толқынның
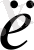 ұзындығын анықтап, Герц тәжірибесінің нәтижесінде электромагниттік толқынның
ұзындығын анықтап, Герц тәжірибесінің нәтижесінде электромагниттік толқынның
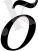 жылдамдығын тапты:
жылдамдығын тапты:
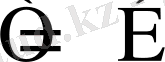 (1. 3)
(1. 3)
Тәжірибеде анықталған электромагниттік толқынның жылдамдығы Максвелл болжаған жылдамдыққа тең болады. Электромагниттік толқындардың болуы туралы Максвелл гипотезасы электромагниттік толқындардың теориясына айналды.
Электромагниттік толқынның негізгі қасиеттерімен танысайық
- Максвелл теориясы бойынша диэлектрлік өтімділігіжәне магниттік өтімділігіортада электромагниттік толқынның таралу жылдамдығын (фазалық)
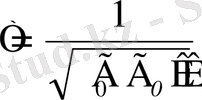 (1. 4)
(1. 4)
Вакуум үшін (
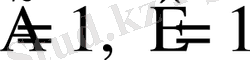 ) электромагниттік толқынның жылдамдығы жарық жылдамдығына тең болады:
) электромагниттік толқынның жылдамдығы жарық жылдамдығына тең болады:
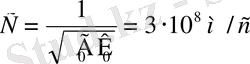 (1. 5)
(1. 5)
Жалпы жағдай үшін
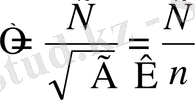 (1. 6)
(1. 6)
Мұндағы n - ортаның сыну көрсеткіші. Бұл Максвелге жарықтың электромагниттік теориясын жасауға мүмкіндік береді.
- Толқын х осінің бойымен таралсын делік. Сонда монохроматтық толқынның жазық теңдеуі
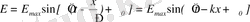 (1. 7)
(1. 7)
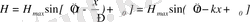 (1. 8)
(1. 8)
Мұндағы Е және Н - лездік, ал
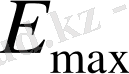 ,
,
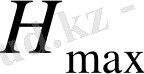 - электрлік және магниттік өрістердің кернеуліктерінің амплитудалық мәндері,
- электрлік және магниттік өрістердің кернеуліктерінің амплитудалық мәндері,
 - тербелістің циклдік жиілігі,
- тербелістің циклдік жиілігі,
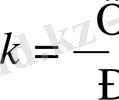 - толқындық сан,
- толқындық сан,

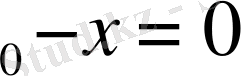 болғандағы бастапқы фаза.
болғандағы бастапқы фаза.
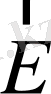 және
және
 векторлары бірдей жиілікте және бірдей фазада тербеледі, сонымен қатар, олар толқынның таралу бағытына және өзара перпендикуляр бағытта болады. Толқынның таралу бағытында х осі бойымен ешбір тербеліс болмайды.
векторлары бірдей жиілікте және бірдей фазада тербеледі, сонымен қатар, олар толқынның таралу бағытына және өзара перпендикуляр бағытта болады. Толқынның таралу бағытында х осі бойымен ешбір тербеліс болмайды.
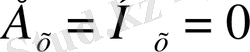 . Бұл электромагниттік толқын көлденең толқынға жататындығын білдіреді.
. Бұл электромагниттік толқын көлденең толқынға жататындығын білдіреді.
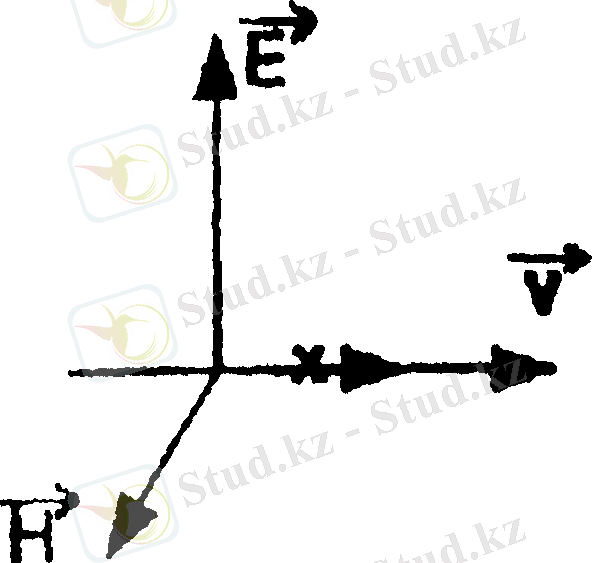
Сурет 4 Көлденең толқынның сызбасы
3 Біртекті және изотопты ортада электромагниттік өрісті тудыратын зарядтар мен токтардан қашықтау жерде айнымалы электромагниттік өрістің кернеулік векторлары
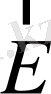 және
және
 дифференциалдық теңдеулермен сипатталады.
дифференциалдық теңдеулермен сипатталады.
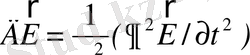 (1. 9)
(1. 9)
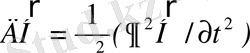 (1. 10)
(1. 10)
- Электромагниттік толқын өзінің таралу бағытында энергия тасымалдайды. Электромагниттік өрістің энергиясының көлемдік тығыздығы электр және магнит өрістерінің энергияларының көлемдік тығыздықтарының қосындысына тең.
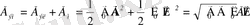 (1. 11)
(1. 11)
5. Бірлік уақыт ішінде көлденнең аудан бірлігінен толқын арқылы тасымалданатын энергия мөлшерін толқынның қарқындылығы деп атайды.
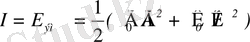 (1. 12)
(1. 12)
(9) -формуладан көрініп тұрғандай толқынның қарқындылығы амплитуданың квадратына тура пропорционал болады.
6. Максвеллдің теориясы бойынша бетке түсірілген электромагниттік толқын қысым түсіреді. Ол қысым
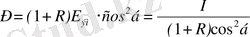 (1. 13)
(1. 13)
Мұндағы R - шағылу коэффициенті,
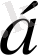 - түсу бұрышы. Айналық бет үшін R=1, ал абсолют қара бет үшін R=0, I - түскен толқынның қарқындылығы.
- түсу бұрышы. Айналық бет үшін R=1, ал абсолют қара бет үшін R=0, I - түскен толқынның қарқындылығы.
Био - Савар - Лаплас заңына сәйкес тогы бар өткізгіштің айналасында магнит индукция сызықтары тұйықталған магнит өрісін тудырады; мұндай өріс құйынды өріс деп аталады. Айнымалы ток өтіп жаткан өткізгіштің төңірегінде айнымалы магнит өрісі пайда болады.
Айнымалы ток тұрақты ток сияқты емес, ол конденсаторлар арқылы өтеді, бірақ бұл ток өткізгіштік ток емес; ол ығысу тогы деп аталады. Ығысу тогы дегеніміз уақыт бойынша өзгеріп отыратын электр өрісі, ол айнымалы өткізгіштік тогы тәрізді, айнымалы магнит өрісінің көзі болып табылады. Біртекті изотропты ортада ығысу тогының тығыздык векторы
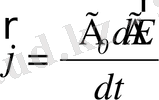 (1. 14)
(1. 14)
мұндағы
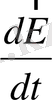 - электр өрісінің кернеулік векторының өзгеріс жылдамдығы.
- электр өрісінің кернеулік векторының өзгеріс жылдамдығы.
Электр өрісінің кернеулігінің уақыт байынша өзгеруінен кеңістіктің әрбір нүктесінде айнымалы құйынды магнит өрісі пайда болады. Пайда болатын магнит өрісінің В векторлары Е векторға перпендикуляр жазықтықта жатады.
Магнит өрісінің индукциясының уақыт бойынша өзгеруінен кеңістіктің әрбір нүктесінде құйынды электр өрісі пайда болады. Пайда болатын электр өрісінің Е кернеулік векторлары магнит индукциясының В векторына перпендикуляр жазықтықта жатады.
Айнымалы электр және магнит өрістерінің бір-бірімен ажырамас жиынтығы электромагниттік өріс деп аталады.
Электромагниттік толқын - бұл кеңістікте таралатын айнымалы электромагниттік өріс. Шексіз кеңістікте таралатын электромагниттік толқындағы электр жөне магнит өрістерінің кернеулік векторлары (Е және В өзара перпендикуляр, ал багыты Е жөне В векторлары жатқан жазықтыққа перпендикуляр болады.
Электромагниттік толқындардың вакуумдегі таралу жылдамдығы олардың толқын ұзындығына тәуелсіз және с = 2, 997925 *10 8 м/с. Электромагниттік толқындардың басқа орталардағы таралу жылдамдығы вакуумдегі жылдамдығынан кіші болады:
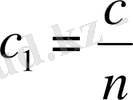 (1. 15)
(1. 15)
Мұндағы n - ортаның сыну көрсеткіші.
Электромагниттік толқындармен энергия тасымалданады. Сәулелену агынының беттік тығыздығы
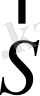 - модулі бойынша толқынның таралу бағытына перпендикуляр орналасқан ауданы 1м
2
жазықтық арқылы өтетін энергия ағынына тең векторлық шама:
- модулі бойынша толқынның таралу бағытына перпендикуляр орналасқан ауданы 1м
2
жазықтық арқылы өтетін энергия ағынына тең векторлық шама:
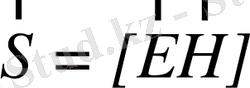 (1. 16)
(1. 16)
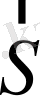 вектор
Пойнтинг векторы
деп аталады; оның бағыты энергияның таралу бағытымен бірдей түседі.
вектор
Пойнтинг векторы
деп аталады; оның бағыты энергияның таралу бағытымен бірдей түседі.
Электромагниттік толқындардың шығарылуы үдемелі қозғалатын зарядталған бөлшектер электромагниттік толқындар шығарады.
Зарядтарының арақашықтығы гармоникалық заңның негізінде өзгеретін диполь электромагниттік толқындар шығарады; дипольдің сәулелену ағыны
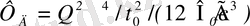 (1. 17)
(1. 17)
мұндағы
 -дипольдің заряды,
-дипольдің заряды,
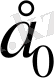 - электрлік тұрақты,
- электрлік тұрақты,
 -бұрыштық жиілік, с - толқынның вакуумдегі жылдамдығы, Ф
д
- бір се
кунд
ішінде шығарылатын орташа энергия.
-бұрыштық жиілік, с - толқынның вакуумдегі жылдамдығы, Ф
д
- бір се
кунд
ішінде шығарылатын орташа энергия.
Айнымалы ток өтіп жатқан кез келген өткізгіш электромагниттік толқындардың көзі болып табылады. Сәулеленудің ең эффективті көзі - сәуле көзінің мөлшерінің сәулеленудің толқын ұзындығымен шамалас болуында. Электромагниттік толқындарды эффективті шығарушы (немесе қабылдаушы) өткізгіштер
антенналар
деп аталады. Өзіндегі ток күші
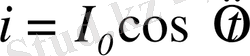 гармоникалық заңмен өзгеріп отыратын сызықтық
гармоникалық заңмен өзгеріп отыратын сызықтық
 ток элементі электромагниттік толқындар шығарып, онда электр және магнит өрістерінің кернеуліктері сәйкес түрде
ток элементі электромагниттік толқындар шығарып, онда электр және магнит өрістерінің кернеуліктері сәйкес түрде
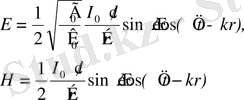 (1. 18)
(1. 18)
болады, мұндағы - ток элементін бақылау нүктесімен қосатын түзу мен өткізгіштегі токтың бағытының арасындағы бұрыш,
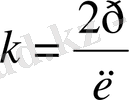 - толқындық сан,
- толқындық сан,
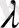 - толқын ұзындығы, r - ені мен кернеулігі анықталатын А нүктесінің арақашықтығы, әрі r>>
- толқын ұзындығы, r - ені мен кернеулігі анықталатын А нүктесінің арақашықтығы, әрі r>>
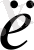 ,
,
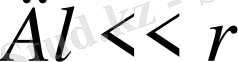
Сызықтық ток элементі тудыратын Ф і сәулелену ағыны келесідей болады (5-суреттегідей) .
(1. 19)
Сурет 5 Сызықтық ток элементінің ағыны
Электромагниттік толқындар басқа түрдегі толқындар тәрізді жұтылады, шағылады және сынады. Бұл құбылыстарға оңай көз жеткізуге болады.
Осы кездегі радиотехникалық құрылғыларға электромагниттік толқындардың қасиеттерін бақылайтын өте көрнекті тәжірибелер жүргізуге болады. Сонда бәрінен де сантиметрлік диапазондағы толқындарды пайдаланған дұрыс. Бұл толқындар аса жоғары жиілікті (АЖЖ) арнаулы генератор арқылы таратып шығарылады. Генератордың электрлік тербелістеріне дыбыстікіндей жиілікпен модуляция жасалынады. Қабылданған сигнал детектрленгеннен кейін дыбыс зорайтқышқа жіберіледі. Рупор антенасы рупор түріндегі қабылдағыш антенна оның өсі бойымен таралатын толқындарды тұтады. Қондырғының жалпы түрі 6-суретте кескінделген.
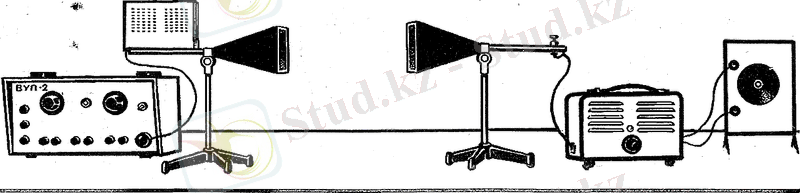
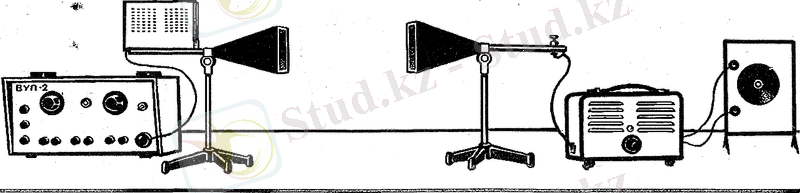
Сурет 6 Радиотехникалық қондырғының жалпы түрі
Электромагниттік толқындардың шағылуы егер диэлектрикті металл пластинкамен алмастырылса, онда дыбыс естілмей қалады. Шағылу салдарынан толқындар қабылдағышқа жетпейді. Шағылу, механикалық толқындар жағдайындағыдай, түсу бұрышына тең бұрышпен байқалады. Осыған көз жеткізу үшін рупорларды үлкен қаңылтыр металмен бірдей бұрыштар жасайтындай етіп орналастырады (7-сурет) . Егер қаңылтырды алып қойса немесе оны бұрса, дыбыс жоғалады.
Таратқыш жөне қабылдағыш рупорлардың арасына металл қаңылтыр қойылса, дыбыс естілмейді. Сол себепті электромагниттік толқын металл қаңылтырдан өте алмай кері шағылады. Егер генератордың рупорын 7-суретте көрсетілгендей бағыттасақ, онда кабылдаушы антенна түсу бұрышына тең бұрышпен шағылатын электромагниттік толқынды қабылдайды. Оны дыбыстың жақсы естілгенінен байқаймыз. Электромагниттік толқынның металл бетінен шағылуын түсіндіру оңай. Металға келіп түскен толқынның электр өрісінің әсерінен металл бетінде еркін электрондардың еріксіз тербелістері қоздырылады. Осы еріксіз тербелістердің жиілігі электромагниттік толқынның жиілігіне тең. Бетке түскен электромагниттік толқынның энергиясы металдағы еркін электрондардың еріксіз тербелістерін қоздыруға жұмсалады. Толқын металдан өте алмайды, металл бетінің өзі екінші реттік толқын көзі болып табылатын болғандықтан, шағылады. Диэлектриктен толқынның шағылуы әлсіз, өйткені диэлектрикте электромагниттік толқынның әсерінен байланысқан электрондардың еріксіз тербелістері қоздырылады. Бірақ олардың еріксіз тербелістерінің амплитудасы металдағы еркін электрондардың еріксіз тербелістерінің амплитудасынан анағұрлым кіші. Сондықтан толқынның диэлектриктен шағылуы нашар болады.
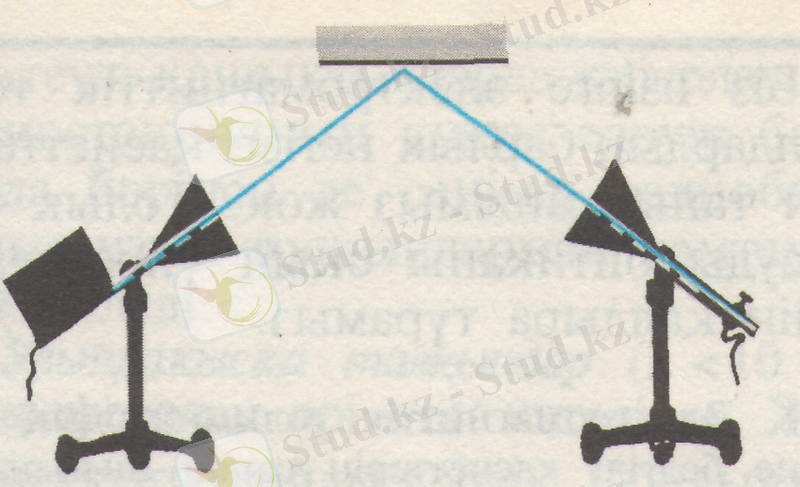
Сурет 7 Шағылуға көз жеткізге арналған рупор
Электромагниттік толқындардың сынуы электромагниттік толқындар диэлектрик шекарасында өз бағытын өзгертеді (сынады) . Мұны парафиннен жасалған үлкен үш бұрышты призманы пайдаланып көруге болады. Шағылуды тәжірибеде көрсеткен сияқты рупорларды бір-бірімен бұрыш жасайтындай етіп орналастырады. Қаңылтырды призмамен алмастырады (8-сурет) . Призманы алып қойып немесе оны бұрса, дыбыстың жоғалып кеткенін байқайды. Электромагнитгік толқынның сынуын парафинмен толтырылған үшбұрышты призманы пайдаланып бақылауға болады. Таратқыш антеннаның рупорын 8-суреттегідей бағыттаймыз. Қабылдаушы антенна толқынды тіркемейді. Енді диэлектрик болып табылатын парафиннен жасалатын призманы суретте көрсетілгендей орналастырайык, сонда антенна толқынды тіркейді. Демек, электромагниттік толқын екі ортаны бөліп тұрған ауа-парафин және парафин-ауа шекараларынан өткен кезде сынады. Электромагниттік толқын бір ортадан екінші ортаға өткенінде сыну заңының орындалатынын зерттеулерден көрген болатынбыз.
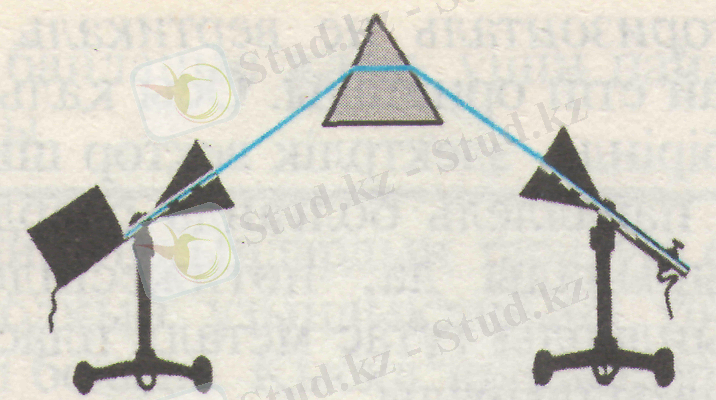
Сурет 8 Парафиннен жасалған үш бұрышты призма
Электромагниттік толқынның жұтылуы рупорларды бір-біріне қарама-қарсы қойып, олардың арасына түрлі диэлектриктер, мысалы, фанера, плексиглас және т. б. қойсақ, толқынның жұтылатынын байқауға болады. Жұтылу дәрежесі әр түрлі диэлектриктер үшін де әр түрлі болады.
Электромагниттік толқындардың поляризациясы электромагниттік толқынның Е жөне В векторларының бір-біріне және толқынның таралу бағытына перпендикуляр болуы оның көлденең толқын екендігін көрсетеді. Таратқыш антеннадан шығатын толқынның электр өрісінің кернеулік Е векторының тербелістері белгілі бір жазықтықта өтеді. Ал магнит индукциясының В векторының тербелістері оған перпендикуляр жазықтықта жасалады. Өріс тербелістері бір бағытта өтетін электромагниттік толқынды поляризацияланған толқын деп атайды.
Поляризация латынның рolus , гректің polos - полюс, осьтің шеті деген сөздерінен алынған. Толқын шығаратын антеннаның рупоры мен қабылдағыштың арасына металл шыбықтан жасалынған торларды (9-сурет) орналастырайық.
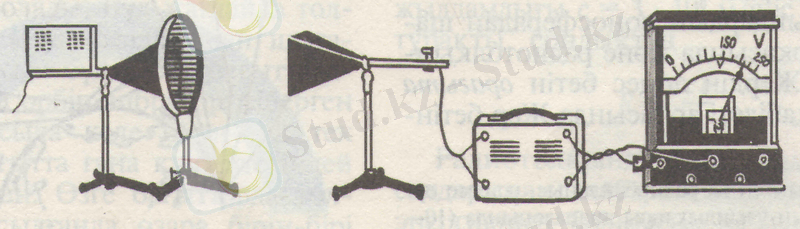
Сурет 9 Антенна мен қабылдағыш арасындағы байланыс
Тордың екеуін де вертикаль не горизонталь бағыттай отырып, толқынның өтуін гальванометр арқылы тіркейміз. Бұл жағдай электр өрісінің кернеулік векторы
 шыбықтарға перпендикуляр қалпында байқалады. Егер екінші торды 90°-қа бұрсақ, онда толқын шыбықтардан өтпей қалады.
шыбықтарға перпендикуляр қалпында байқалады. Егер екінші торды 90°-қа бұрсақ, онда толқын шыбықтардан өтпей қалады.
Демек, электромагниттік толқын - көлденең толқынға жатады. Электр өрісінің кернеулік векторы металл шыбықтарға параллель бағытталғанда, оларда еркін электрондардың еріксіз тербелістері қозады да толқын шағылады. Кернеулік векторы шыбықтарға перпендикуляр бағытталғанда, еркін электрондардың еріксіз тербелістері көлденең болғандықтан, олардың амплитудасы мардымсыз. Электромагниттік толқын шағылмай өтіп кетеді. Егер электромагниттік толқын көлденең емес, қума толқын болса, онда тордың кез келген қалпында ол шыбықтардан өтіп кеткен болар еді. Пәтерлерден теледидар антеннасын орнатқанда электромагниттік толқынның поляризацияланғанын ескеруіміз қажет. Антеннада қозатын индукциялық токтың амплитудасы максимал болады, егер кернеулік векторы антеннаға параллель қалпын сақтайтын болса.
Электромагниттік толқындардың интерференциясы. Кеңістікте екі немесе бірнеше таратқыш антеннадан таралған электромагниттік толқындар бір-бірімен қабаттасады. Жиіліктері бірдей екі толқын қосылғанда қорытқы толқын амплитудасының арту немесе кему құбылысын толқындардың интерференциясы дейді.
Бірдей фазамен тербелетін екі электромагниттік толқын кеңістіктің бір нүктесіне келіп жеткенде
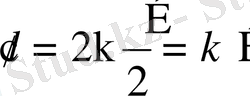 (1. 20)
(1. 20)
шарты орындалса, интерференция нәтижесінде қорытқы тербеліс амплитудасы максимал болады. Мұндағы
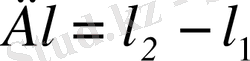 толқындардың жол айырымы,
к
= 0, 1, 2, 3, . . .
толқындардың жол айырымы,
к
= 0, 1, 2, 3, . . .
Егер толқындардың жол айырымы
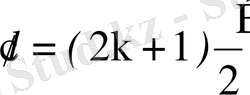 (1. 21)
(1. 21)
тақ санды жарты толқынға тең болса, онда интерференцияның минимум шарты орындалады. Қорытқы тербеліс сол нүктеде минимал болады. Электромагниттік толқындардың интерференциясын бақылау үшін таратқыш пен қабылдағыштың рупорларын 9-суреттегі сияқты қарама-қарсы орналастырып, горизонталь бағыттағы металл қаңылтырды жоғарыдан төмен қозғалтайық. Сонда дыбыстың біресе күшейіп, біресе бәсеңдегенін байкаймыз. Рупордан шығатын толқынның біраз бөлігі қабылдағыш антеннага түседі. Қалган бөлігі металл бетінен шағылып барып түседі. Металл каңылтырды жоғары немесе төмен козғалта отырып, тура толқын мен шағылған толқынның жол айырымын өзгертеміз. Интерференцияның максимум немесе минимум шарттарының қайсысы орындалатынына байланысты, дыбыс не күшейеді, не әлсірейді.
Электромагниттік толқындардың көлденеңдігі электромагниттік толқындар көлденең толқындар болып табылады. Бұл толқынның электромагниттік өрісінің
 және
және
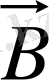 векторының оның таралу бағытына перпендикуляр екендігін көрсетеді.
векторының оның таралу бағытына перпендикуляр екендігін көрсетеді.
Рупордан шығатын толқынның электр өрісі кернеулігінің тербелістері белгілі бір жазықтықта өтеді, ал магнит индукциясы векторының тербелістері -оған перпендикуляр жазықтықта жатады. Тербелістері белгілі бір бағытта өтетін толқындар поляризацияланған деп аталады. Детекторы бар қабылдағыш рупор тек белгілі бағытта поляризацияланған толқынды ғана қабылдай алады.
Мұны хабарлағыш не қабылдағыш рупорды 90°-қа бұру арқылы аңғаруға болады. Сонда дыбыс жоғалады.
Поляризацияны генератор мен қабылдағыш арасына параллель металл шыбықтардан істелген тор орнатып, бақылайды (10-сурет) . Торды шыбықтар горизонталь не вертикаль тұратындай етіп орнатады. Осы қалыптардың бірінде, электрлік вектор шыбықтарға параллель болғанда олардағы ток қоздырылады да, нәтижесінде тор толқындарды тұтас металл пластинаша шағылдырады.
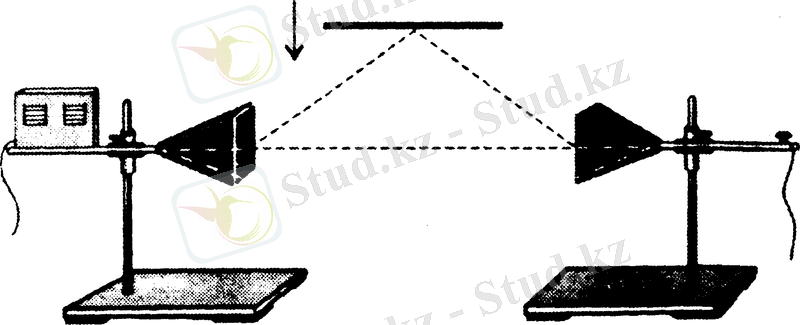
Сурет 10 Толқын шығаратын рупор
 векторы шыбықтарға перпеңдикуляр болғанда ток қоздырылмайды да, электромагниттік толқын өтіп кетеді.
векторы шыбықтарға перпеңдикуляр болғанда ток қоздырылмайды да, электромагниттік толқын өтіп кетеді.
Электромагниттік толқындардың дифракциясы толқындардың түзу сызықты таралуынан ауытқуының бөгеттерді орағытып өтуін толқынның дифракциясы деп атайды Толқын жолындағы бөгеттердің өлшемдері толқын ұзындыгынан кіші немесе онымен шамалас болған жағдайларда толқын дифракциясы айқын байқалады. Электромагниттік толқындардың дифракциясын 11-суретте көрсетілген қондырғының көмегімен бақылайды. Аса жоғары жиілікті генератор мен қабылдағыштың арасында жіңішке саңылауы бар металл экран тұр. Қабылдағыштың орнын ауыстыра отырып, тербеліс амплитудасының максимумдары мен минимумдары кезек ауысатынын көреміз. Бұл саңылаудың шетін орағытып өтетін толқындардың дифракциясы нәтижесінде ғана мүмкін болады. Ендеше электромагниттік толқындарда дифракция құбылысы байқалады [1] .
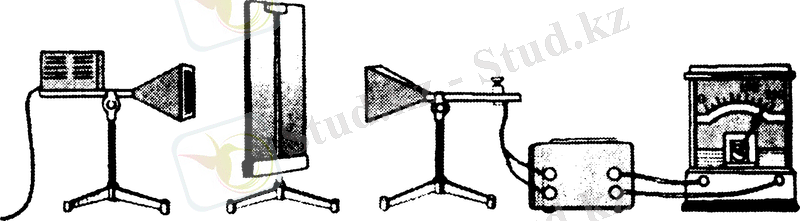
Сурет 11 Толқынның дифракциясын бақылайтын қондырғы
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz