Функцияларды енгізу терезесі

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 61 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ ҒЫЛЫМ ЖӘНЕ БІЛІМ МИНИСТРЛІГІ

Ы. АЛТЫНСАРИН АТЫНДАҒЫ АРҚАЛЫҚ МЕМЛЕКЕТТІК ПЕДАГОГИКАЛЫҚ ИНСТИТУТЫ

Жаратылыстану және ақпараттандыру факультеті

Математика, физика және информатика кафедрасы

ДИПЛОМДЫҚ ЖҰМЫС

MATHCAD ПРОГРАММАСЫНДАҒЫ САНДЫҚ ӘДІСТЕР

Орындаған: 050109 «Математика» мамандығының

ІV курс студенті Татен М. С.

Ғылыми жетекшісі:

аға оқытушы Еденов Ә. Е.

Арқалық - 2009

МАЗМҰНЫ

КІРІСПЕ. …. . 3

І. MATHCAD ПРОГРАММАЛЫҚ ПАКЕТІ . . . 5

1. 1. MATHCAD программалық пакетінің мүмкіндіктері . . . 5

1. 2. Программа құрылымы7

1. 3. Математика саймандар қатарының қызметі . . . ……. 12

ІІ. MATHCAD ПРОГРАММАСЫНДАҒЫ САНДЫҚ ӘДІСТЕР………. . … . . . 24

2. ТЕҢДЕУДІҢ ТҮБІРІН ТАБУ. . …24

2. 1. Туынды түріндегі функциялар. . ……27

2. 2. Полином түбірлерін табу. . …. 28

2. 3. Символдық түрлендіру арқылы теңдеудің түбірін табу. ……28

2. 4. MathCAD 2000 теңдеудің түбірін іздеу. … . . . 29

3. ТЕҢДЕУ МЕН ТЕҢСІЗДІКТЕР ЖҮЙЕСІН ШЕШУ … . …30

3. 1. Сызықты және сызықты емес теңдеулер мен теңсіздіктер жүйесін шешу . . . 30

3. 2. Сызықты теңсіздіктер мен теңдеулер жүйесін шешу. …31

3. 3. Теңдеу жүйесінің символдық шешуі . . . 32

3. 4. Функцияның экстремумдарын табу. …. 32

4. АНЫҚТАЛҒАН ИНТЕГРАЛДЫ ЕСЕПТЕУ. . …35

4. 1. Ромберг әдісі. …. . 35

4. 2. Анықталған интеграл. …37

5. ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕРДІ ШЕШУ38

5. 1. Қарапайым дифференциалдық теңдеулер . . . 38

5. 2. n-ші ретті дифференциалдық теңдеулер. …. 41

5. 3. Дифференциалдық теңдеулер жүйесі. …. . 43

5. 4. Қарапайым дифференциалдық теңдеулер: шектік есептер . . . 48

5. 5. Дербес туындылы дифференциалдық теңдеулер50

ҚОРЫТЫНДЫ. . 66

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ. 67

ҚОСЫМШАЛАР . . . 69

КІРІСПЕ

Компьютерлік техниканың дамуы ғылым мен техниканың практикалық есептерін шығарудың әртүрлі логикалық әдіс-тәсілдері дамуда. Қазіргі жағдайда кез келген қолданбалы есептерді шешіп, бағдарламасын құрып, тестілеуге болады. Инженер-зерттеуші сандық есептеулердің қорытындысын алу және әртүрлі параметрлер әсерінің бағасын білу үшін қазіргі заманда компьютерлік технологияға сүйенеді. Бірақ компьютерді қолдану практикалық мәселелердің шешімін жеңілдетпей, оны күрделендіріп жібергендей. Математикалық және ғылыми-техникалық есептеулер дербес компьютерді қолданудың маңызды сферасы болып табылады. Көбінесе олар жоғары дәрежеде жазылған, мысалы Бейсик немесе Паскаль тіліндегі программалардың көмегімен орындалады. Бүгінгі уақытта бұл жұмысты дербес компьютерді қолданушы кез-келген адам әр кезде орындай алмайды. Ол үшін ол адам программалау тілін және қазіргі кезде өте күрделі математикалық есептеулердің сандық әдістерін үйренуге мәжбүр болады. Кей жағдайларда осының салдарынан физик, химик немесе инженер мамандарының қолынан шындықтан алыс программалар келіп шығады. Сонымен бағдарламашылар бір есепті шығару үшін ұзақ уақыт бойы оның бағдарламасын құрып, тек содан кейін ғана есептеулер жүргізген. Бұл жұмыстар бір жағынан қолайлы болғанымен, қарапайым қолданушылар үшін тиімсіз әрі қиын соғады, өйткені әр адам бағдарламалау тілін біле бермейді. Сөйтіп бұл мәселелердің барлығын компьютерлік математикалық жүйелерді құруға көшті.

Компьютерлік математика - ғылым мен техникадағы жаңа бағыт. Ол классикалық математика мен информатиканың түйісуінен туындайды. Компьютерлік математиканың маңыздылығы оның программалық жүйемен қамтамасыз етілуінде және кез-келген математикалық есептерді шешу қабілеттілігінде. Компьютерлік математика жүйесі батыстың Mathsoft, MathWors, Maple, Wolfram секілді фирмаларында жасалған. Бұл жүйе алдыңғы қатарлы, озық информациялық технологияларды білім мен ғылым саласында ортақ пайдаланатыны негізінде қазіргі күні барлық елдердің игілігіне айналып отыр. Компьютерлік математикадағы танымал жүйе MathCAD ғылым мен білімнің және техниканың әртүрлі аймақтарын автоматтандыру үшін математикалық есептеулерге арналған. Жүйенің аталуы екі сөзден құралған, яғни MATHematica (математика) және CAD (Computer Aided Desing - автоматты жобалау жүйесі немесе АЖЖ) . Сондықтан MathCAD-ты математикалық автоматты жобалау жүйесі деп атауға болады.

MathCAD программасы қарапайым арифметикалық есептерден бастап, қиын сандық әдістер көмегімен шешілетін есептерді шығару үшін, ғылыми және инженерлік есептеулерді жүргізуге арналған математикалық редактор. Бұл құрал көмегімен әртүрлі есептерді шешуге, теңдеулер графиктерін құруға және оларды көрнекі түрде көруге болады.

Сонымен бірге MathCAD-тың көптеген құрастырылған қарапайым арнайы және статистикалық функциялары бар. Математикалық функцияларды ендіруді жеңілдету үшін арнайы түймелер қолданылады, ол терезеде математикалық бөлшектерге бөлінген функцияның толық түсіндірмесімен шығарады. Жай есептеулер MathCAD-та өте тез орындалады және бұл программаның басты жетістігі әртүрлі функциялардың графиктерін бір координата жазықтығында салуда болып табылады. Сондай-ақ, MathCAD программасындағы кітапхана, кеңейтілу пакеті және компьютерлік математика жүйесі - мыңдаған жылдар бойы жинақталған математикалық білімді топтайды. Қорыта айтқанда, аталған жүйені бүгін уақыт талабына сай электронды оқулықтар жасауда кеңінен қолданған тиімді.

MathCAD-тың көмегімен кітап, диссертация, ғылыми есеп, дипломдық және курстық жобаларды тек әр түрлі үлгідегі сапалы мәтінмен ғана емес, ең күрделі математикалық формула жиынтығымен, есептеулермен, графиктік көріністермен дайындауға болады.

Жұмыстың мақсаты

Бұл жұмыстың мақсаты қазіргі заманның талабына сай күннен күнге дамып отырған ақпараттық технологиялардың көмегімен әртүрлі математикалық қарапайым есептер мен сандық есептерді шығарудың, соның ішінде теңдеулер мен теңсіздіктерді шешу, анықталған интегралды есептеу, дифференциалдық теңдеулерді шығару үшін қолданылатын жаңа компьютерлік бағыттың қолданылуы. Ол программалық пакеттің құрылымымен таныстырып, маңыздылығын мен қажеттілігін көрсету.

Тақырыптың өзектілігі

Компьютерлік технологияның дамуы ақпараттық технологияның күнделікті өзгеруіне әкеліп, ғылымы мен техника саласындағы, әсіресе математика саласының есептерін, оның ішінде теңдеулер мен теңсіздіктерді шешу, анықталған интегралды есептеу, дифференциалдық теңдеулерді шешу үшін қолдануға ыңғайлы MathCAD программалық пакетінің қызметі жайлы түсіндіру.

Дипломдық жұмыстың құрылымы

Кіріспе бөлімінде жаңа заман талабына сай дамып келе жатқан жаңа ақпараттық, компьютерлік технологиялардың болуы туралы айтылды.

Жұмыстың негізгі бөлімі екі тараушадан тұрады. Біріншісінде MathCAD программалық пакетінің мүмкіндіктері, программа құрылымы және оның математика саласында қолданылуы жайлы, арнайы математика саймандар қатары туралы жазылған. Екінші тарауында осы программалық пакеттің көмегімен теңдеулер мен теңсіздіктерді шығаруға, анықталған интегралды есептеуге, дифференциалдық теңдеулерді шешуге қолданылуы, оның қосымша функцияларының қызметі туралы айтылып, есептер және оның графиктері көрсетілген.

І. MATHCAD ПРОГРАММАЛЫҚ ПАКЕТІ

MATHCAD ПРОГРАММАЛЫҚ ПАКЕТІНІҢ МҮМКІНДІКТЕРІ

Компьютерлік математика - ғылым мен техникадағы жаңа бағыт. Ол классикалық математика мен информатиканың түйісуінен н туындайды. Компьютерлік математиканың маңыздылығы оның программалық жүйемен қамтамасыз етілуінде және кез-келген математикалық есептерді шешу қабілеттілігінде. Компьютерлік математика жүйесі батыстың Mathsoft, MathWors, Maple, Wolfram секілді фирмаларында жасалған. Бұл жүйе алдыңғы қатарлы, озық информациялық технологияларды білім мен ғылым саласында ортақ пайдаланатыны негізінде қазіргі күні барлық елдердің игілігіне айналып отыр. Компьютерлік математикадағы танымал жүйе MathCAD ғылым мен білімнің және техниканың әртүрлі аймақтарын автоматтандыру үшін математикалық есептеулерге арналған. Жүйенің аталуы екі сөзден құралған, яғни MATHematica (математика) және CAD (Computer Aided Desing - автоматты жобалау жүйесі немесе АЖЖ) . Сондықтан MathCad-ты математикалық автоматты жобалау жүйесі деп атауға болады.

MathCAD программасының мұндай мүмкіндіктері электронды сабақтар, лекциялар курсы, электронды кітаптар жазуда маңызды жабдыққа айналып отыр. Сонымен бірге компьютерлік математика жүйесі көркемөнер, графика, лингвистика саласында кеңінен қолданыс табуда. MathCAD-тың жаңа нұсқасында құжаттардың көркем түсті эффектілі құрылғы және графикті анимациялау, дыбысты қосып шығару мүмкіндігі қосылған. Осы артықшылығына байланысты мәтіндік, формулалық және графиктік редакторлар қуатты есептеуіш потенциалды орта жүйесімен бірігеді. Өте күрделі тапсырмаларды шешу үшін математикалық және графикалық жүйелер және олардың бірігуі қарастырылған. Бұл жүйе әртүрлі математикалық, графикалық және офистік жүйе қатарымен кеңейтілген интегралдауды қамтамасыз етеді.

MathCAD-ты тек қана математикалық есептерді шешу үшін емес басқа да қуатты инженерлік автоматтандырылған жобалау жүйесін дайындаумен бірге, графиктерді, бірнеше графиктерді бір мезгілде салу мүмкіндігі ескерілген. MathCAD - барлық функциялардың графиктерін көрнекі түрде, әсем көрсетуімен бірге, математикалық таңбаларды, символдарды палитра көмегімен енгізудегі артықшылығы көрсетілген. Жалпы жағдайда, MathCAD жүйесі келесі компоненттерден тұрады:

құжаттар редакторы - математикалық өрнектердің, графиктердің, үлгілер және мәтіндік түсініктемелердің мүмкіндіктерімен кірістірілген редакторы;
ресурстар орталығы - интегралданған ресурстар жүйелері;
электрондық кітап - ғылым және техника аймақтарында әр алуан типтік есептер жазылған электрондық кітап;
анықтамалық жүйе - тақырыптық және индекстік каталог бойынша берілгендердің анықтамасын алу үшін және басқа кілттік сөз немесе фраза бойынша керекті берілгендерді іздеуге арналған жүйе;
броузер Интернет - Интернетке шығатын жеке құрал.

Редакторлеу режимінде бір мезгілде бір терезеден басқа объектіге өтуіне және құжаттар қатарымен жұмыс істеуге болады. Сондай-ақ кез-келген графикалық бейнелеу жай немесе күрделі функция графиктерінен суреттік бейнелердің көп түсті дизайны қарастырылған және суреттерді анимациялау құрылғысы енгізілген, видео-файлдық шығармаларды стереофондық дыбыстар арқылы экранға шығару мүмкіндігі бар.

Сонымен бірге MathCAD-тың көптеген құрыстырылған қарапайым арнайы және статистикалық функциялары бар. Математикалық функцияларды ендіруді жеңілдету үшін арнайы түймелер қолданылады, ол терезеде математикалық бөліктеріне бөлінген функцияның толық түсіндірмесін шығарады. Жай есептеулер MathCAD-та өте тез орындалады және бұл программаның басты жетістігі әртүрлі функциялардың графиктерін бір координата жазықтығында салуда болып табылады. Сондай-ақ, MathCAD программасындағы кітапхана, кеңейтілу пакеті және компьютерлік математика жүйесі - мыңдаған жылдар бойы жинақталған математикалық білімді топтайды. Қорыта айтқанда, аталған жүйені бүгінгі уақыт талабына сай электронды оқулықтар жасауда кеңнен қолданған тиімді.

MathCADпрограммалық пакеті:

мәтін мен қатар математикалық өрнектерді форматтап, редакторлеуге арналған қуатты мәтіндік редактор;
қолданбалы сандық әдісті қолдана отырып, әртүрлі есептеулерді орындауға арналған есептегіш процессор;
жасанды интеллектің жүйесі болып табылатын қарапайым есептеулер мен құбылыстарды жүргізуге арналған символдық процессор;
барлық математикалық та, инженерлік те анықтамалар сақталған, интерактивті электрондық кітап ретінде безендірілген анықтамалар.

MathCAD программасының басқа да математикалық редаторлерден ерекшелігі оның WYSIWYG (“What You See Is What You Get” - «что вы видите, то и получите») мұндағы приципімен жұмыс жасауы. Сондықтан оны қолдану өте ыңғайлы, өйткені қандай да бір есептің орындалуын көру үшін оның программасын жазудың қажеті жоқ. Бұның орнына математикалық өрнектерді формулалар редакторы көмегімен енгізіп, есептеулердің нәтижесін көруге болады. Сонымен қатар сол есептеулер нәтижесін бірден қағаз басып шығаруға да болады. Тағы бір ерекшеліктерінің бірі сол бетті Интернет беті ретінде де көруге болады.

MathCAD программасын құрушылар барлық мүмкіндікті жасаған, атап айтқанда, әрбір қолданушы, яғни бағдарламалау тілін меңгермеген қолданушының өзі де есептеулерді бірден жүргізе алады. Бұл программамен жұмыс жасау үшін қолданушы қарапайым компьютерді қолдану мүмкіндіктерін меңгерсе болғаны. Екінші жағынан кәсіби программистер мүмкіндіктерінің өздерінің білімдері арқылы, яғни есептеулер жүргізу кезінде өздері құрған программаларды енгізе алады.

Сонымен бұл программа математиктердің бірнеше мәселелерін шеше алады:

математикалық өрнектерді компьютерге енгізу (ары қарай есептеу не құжат құру, не презентация құру, Web - бетін немесе электронды кітап жасау үшін) ;
математикалық есептеулер жүргізу (қарапайым да, сандық әдіс көмегімен де) ;
есептеулер нәтижесінің көмегімен графиктер дайындау;
әртүрлі форматтағы берілгендерді енгізу және нәтижелерін шығару;
баспа құжат түрінде есепті көру;
Web - парақтарын дайындау және оның нәтижесін Интернетте көру;
Математика аймағындағы әртүрлі анықтамаларды алу. ПРОГРАММА ҚҰРЫЛЫМЫ

MathCAD программасы компьютерге қойылып енгізіліп болғаннан кейін 1-суретте көріп отырғандай терезеде жұмыс жасаймыз. Бұл программа Windows ортасындағы барлық программаларға ұқсас келеді.

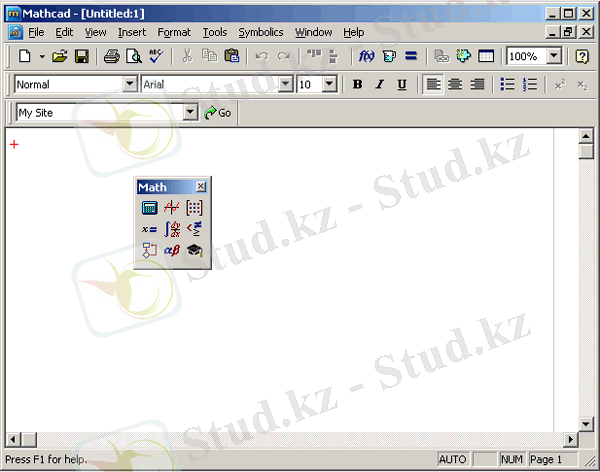
Сурет 1. MathCAD 12 программасының терезе құрылымы

Жоғарыдан төмен тақырып қатары, мәзір қатары, саймандар қатары (стандартты және форматтау) және жұмыс аумағы (worksheet) орналастырылған. Жаңа құжат программаны іске қосқаннан кейін автоматты түрде құрылады. Терезенің ең төменгі жағында қалып күй қатары орналастырылған. Сонымен MathCAD программасының интерфейсі де басқа программаларға әсіресе қарапайым мәтіндік редакторге ұқсас.

Мәтіндік редактордың басқару элементтеріне сәйкес келетін MathCAD программасы Math (Математика) саймандар қатарымен толықтырылған. Осы қатар және тағы да басқа қосымша қатарлар көмегімен теңдеулерді енгізуге болады.

MathCAD программасының терезе құрылымы:

Standard (Стандартная) стандартты саймандар қатары;
Formatting (Форматирование) пішімдеу қатары;
Resources (Ресурсы) ресурстар;
Controls (Элементы управления) басқару элементтері;
Math (Математика) қатары;
Жұмыс аумағы (worksheet) ;
Қалып күй қатары (status line немесе status bar) ;
Көмек беру және жанама мәзірі (pop-up menus немесе context menus) ;
Сұхбат терезелері (dialogs) ;
MathCAD (Mathcad Resources) қосалқы мысалдармен және қосымша ақпаратпен жабдықталған қатары.

Көптеген командаларды мәзір, саймандар қатары көмегімен де пернетақта көмегімен де орындауға болады.

Математикалық және ғылыми-техникалық есептеулер дербес компьютерді қолданудың маңызды сферасы болып табылады. Көбінесе олар жоғары дәрежеде жазылған, мысалы Бейсик немесе Паскаль тіліндегі программалардың көмегімен орындалады. Бүгінгі уақытта бұл жұмысты дербес компьютерді қолданушы кез-келген адам әр кезде орындай алмайды. Ол үшін ол адам программалау тілін және қазіргі кезде өте күрделі математикалық, есептеулердің сандық әдістерін үйренуге мәжбүр болады. Кей жағдайларда осының салдарынан физик, химик немесе инженер мамандарының қолынан шыққандықтан алыс программалар келіп шығады.

Осындай келген жағдайлардан математикалық есептеулерді автоматизациялайтын интегралдаудың программалық жүйесін қолдану арқылы шығуға болады (мысалы MathCAD, MathLAB және тағы басқадай) . Біздің алдымызда сондай жүйелердің бірі MathCAD-тың сызықтық емес теңдеулер жүйесін шығарудағы мүмкіндіктері мен эволюциясын қарастырамыз.

MathCAD - бұл ғылым мен техниканың, білім берудің әр түрлі облыстарында мысалы математикалық есептерді шешуді автоматизациялауға бағытталған компьютерлік математиканың белгілі жүйесі.

MathSoftInc. (АҚШ) фирмасы жүйенің бірінші версиясын 1986 жылы шығарды. MathCAD жүйесінің басты бөліп алатын ерекшелігі оған енгізілген тілде, мұнда математика бойынша трактаттарында, тіпті жалпы ғылыми әдебиеттерде қолданылатын нақты математика тіліне максималды жуық. Жүйемен жұмыс істеуге кіріскенде қолданушы атаулы документтерді дайындайды. Олар бір уақытта есептеу алгоритмінің бейнелеуін, жұмысты басқару программасын және есептеу нәтижесін іске қосады. Сыртқы көрінісіне қарағанда мәтіндер кәдімгі программаға ұқсамайды.

Бүгінде MathCAD-тың әр түрлі версиялары математикалық бағдарланған универсалды жүйе болып табылады. Ол мәтіндік редакторлар және электронды таблицалармен қиын берілетін күрделі есептеулерді жеңіл шешуге мүмкіндік береді. MathCAD көмегімен статья, кітап, диссертация, ғылыми есептеу, дипломдық және курстық жобаларды тек қана сапалы мәтіндермен емес, сондай-ақ жеңіл жүзеге асыратын ең күрделі математикалық формулалар жиынымен, есептеу нәтижесін графикалық қойылымдармен дайындауға болады.

MathCAD жүйесінің жаңа версиясындағы маңызды жетістігі болып кез-келген баспаға шығару құрылғысының белгілі типіндегі настройка, шрифтердің бай жинағы, Windows-тың барлық құралдарын қолдану мүмкіндіктері, әдемі графика және қазіргі уақыттағы көп терезелі интерфейс жатады. Жаңа нұсқада да документтерді әр түрде безендіруде тиімді мүмкіндіктер, қозғалмалы графиктер және дыбыстық сүйемелдеуді жасау қосылған. Ерекше күрделі есептерді шешу үшін басқа математикалық және графикалық жүйелермен бірігу мүмкіндіктері де қарастырылған. Осыдан мынадай жүйелер - интегрирленген жүйелер атауы шығады. Интеграция есептерін шешуде MathCAD-ты жасаушылар ұзаққа кеткен - бұл жүйе түпкі интеграцияны басқа математикалық, графиктік, офистік жүйелермен, толық қатармен қамтамасыз етеді. Осы үшін оған MathConnex арнайы жүйелілік интегратор қосылған. 1999 жылдың жазында жаңаланған нұсқа - MathCAD 2000 жүйесі шықты. Оған графиктік мүмкіндіктердің жақсаруы, есептеу жылдамдығының жоғарлауы, жұмыс тиімділігі, функциялар санының өсуі кіреді.

Кейбір суреттерде көрініп тұрғанымыздай қызыл қосу белгісі бар. Оның көмегімен құжаттағы бос орынды мәтін немесе формуламен толтыруға болады. Бұл сілтемені жылжытып, орынын ауыстыру үшін тышқанмен шерту жеткілікті. Формула аймағында сырт еткізу кезінде сілтеме орнына редакторлеу сызығы пайда болады.

Үнсіз келісім бойынша бұл программада есептеулер нақты уақыт аралығында жүргізіледі, яғни қолданушы сандық және символдың теңдік операторларын енгізе бастаған кезде MathCAD есептеулерді жүргізе бастайды. Кейде қиын да, күрделі ұзақ есептеулерді <Esc> пернесінің көмегімен тоқтата қоюға болады, қайта қалпына келтіру үшін <F9> немесе Tools/Calculate (Сервис/Вычислить) және Tools/Calculate Worksheet (Сервис/Вычислить во всем документе) командаларының көмегімен орындаймыз.

Сонымен қатар MathCAD программасында әртүрлі функцияларды есептеуге болады, оларды бірден енгізіп, мәндерін білуге болады. Ол үшін функция енгізу деп аталатын арнайы терезе бар. Бұл терезе екі бөліктен тұрады: функция категориялары, яғни арнайы, статистикалық, тригонометриялық, логикалық және т. б. категорияларға байланысты функция аттары. Функция аттарын пернетақтадан да енгізуге болады.

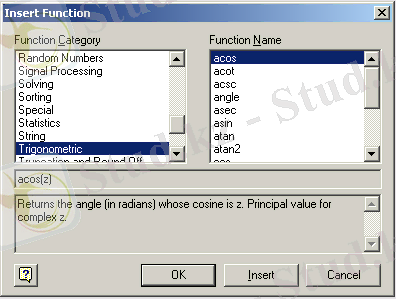
Сурет 2. Функцияларды енгізу терезесі.

Функцияны өрнекке енгізу үшін:

Функцияны қоятын жерді анықтап алу керек.
f(x) жазылымын стандартты саймандар қатарынан басу керек.
Insert Function (Вставить функцию) сұхбат терезесіндегі Function Category (Категория функции) тізімінен функция жататын қажетті категорияны таңдаймыз.
Function Name (Имя функции) тізімінен қажетті функция атын таңдаймыз.
OK-ді бассақ құжатқа қажетті функция енгізіледі.
Кейін функцияның жетіспеуші аргументтерін енгізуге болады. Дәл осы функцияны Math саймандар қатарынан былай енгізуге болады.

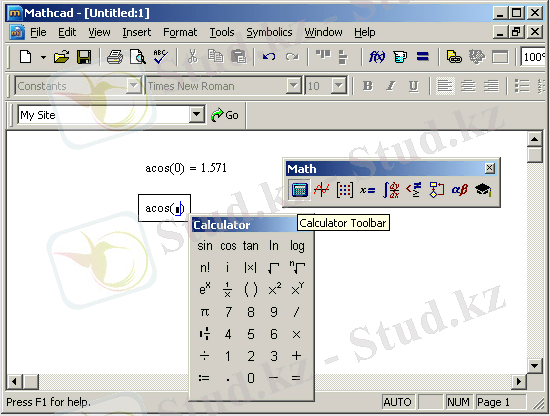
Сурет 3. MathCAD программалық пакетінің жұмыс аймағы.

MATH (МАТЕМАТИКА) САЙМАНДАР ҚАТАРЫНЫҢ ҚЫЗМЕТІ

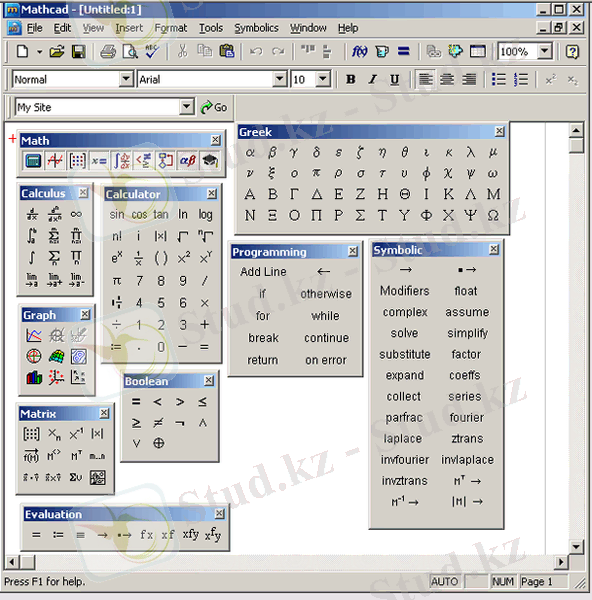
Сурет 4. Негізі және математикалық саймандар қатары.

Math (Математика) - құжатқа математикалық символдар мен операторларды енгізу;
Resources (Ресурсы) - MathCAD ресурстарын тез шешу үшін (мысал, оқулық, электрондық кітап және т. б. ) ;
Controls (Элементы управления) - құжатқа стандартты басқару элементтерін енгізу үшін.

Барлық терезе құрылымына ұқсас түймелер тобы сызық арқылы Math (Математика) саймандар қатары экранға тағы да басқа математикалық операцияларды орындау үшін қажетті тоғыз саймандар қатарын шақыру үшін қолданылады:

Calculator (Калькулятор) - кәдімгі калькуляторға ұқсас қарапайым математикалық операциялар мен есептеулерді орындауға арналған;
Graph (График) - графиктер енгізу үшін;
Matrix (Матрица) - матрица және матрицалық операторды енгізу үшін;
Evaluation (Выражения) - есептеулерді басқаратын операторларды шақыру;
Calculus (Вычисления) - интегралдау, дифференциалдау және қосу операторларын енгізу;
Boolean (Булоны операторы) - логикалық (буловых) операторларын енгізу;
Programming (Программирование) - MathCAD құралы көмегімен программалау;
Greek (Греческие символы) - грек символдарын енгізу;
Symbolic (Символика) - символдың операторларды енгізу.

Барлық символды пернетақтадан енгізе алмаймыз. Мысалы, дифференциалдау және интегралдау белгілері. Ол үшін MathCAD программасында Microsoft Word мәтіндік редакторындағы формулалар редакторына ұқсас арнайы Math (Математика) саймандар қатары бар.

Бұл саймандар қатары математикалық объектілерді (оператор, график, программа элементтері және т. б. ) енгізуге арналған құралдардан тұрады.

Жоғарыда айтып кеткендей қатардың тоғыз арнайы түймелері бар. Әр түйменің өз қызметі бар. Осы қосымша тоғыз тақталар көмегімен әртүрлі математикалық объектілерді енгізуге болады. Әр тақтаға жеке тоқталып кетейік.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.