Мектеп математикасында жай бөлшектер тақырыбын оқытудың дәстүрлі әдістері мен практикалық негіздемесі


МАЗМҰНЫ
КІРІСПЕ . . .
ТАРАУ 1. «ЖАЙ БӨЛШЕКТЕР» ТАҚЫРЫБЫН ОҚЫТУДАҒЫ
ДӘСТҮРЛІ ӘДІС-ТӘСІЛДЕР . . .
1. 1 Бөлшектердің шығу тарихынан . . .
1. 2 Жай бөлшектерге қолданылатын арифметикалық амалдар . . .
1. 3 Мектеп математика курсындағы «Жай бөлшектер»
тақырыбының мазмұны . . .
ТАРАУ 2. «ЖАЙ БӨЛШЕКТЕР» ТАҚЫРЫБЫН ОҚЫТУДАҒЫ
ПРАКТИКАЛЫҚ НЕГІЗДЕМЕ . . .
2. 1 Мектеп математика курсында жай бөлшектерді оқытудың әдістемесі . . .
2. 2. «Жай бөлшектер» тақырыбының оқушылардың
математикалық қабілеттерінің дамуына әсер ету диагностикасы . . .
ҚОРЫТЫНДЫ . . .
ҚОСЫМША . . .
ПАЙДАЛАНЫЛҒАН ДЕРЕКТЕР КӨЗІ . . .
Кіріспе.
Білім берудің қазіргі талабы - анық ашықтың кейпі, яғни тұлғаның жан-жақты іс-әрекеттік қабілетін кеңейтіп, оның құзырын арттыру, жалпы өмірлік және кәсіби құзырын дамыту және қалыптастыру. Жалпы білім беру саласының алдына қойылған осы мақсат ең алдымен бірінші кезекте математикалық білім беру сапасын арттыру мәселелеріне келіп тірелетіні баршаға анық.
Ежелгі замандардан бері математиканың алар орны, оның ғылым мен техниканың қарқанды дамуына қосар үлесі, жас жеткіншектерді тәрбиелеудегі маңыздылығы аз айтылған жоқ. Олай болса, ең алдымен мектептегі математиканы оқытудың негізгі мақсаты:
- Математика - ғылым болмысынан балама ұғымдар. Сондықтан да математика барлық ғылымдардың логикалық негізгі күре тамыры ретінде қарастырылады;
- Математика - ең алдымен оқушылардың дұрыс ойлау мәдениетін қалыптастырады, дамытады және оны шыңдай түседі;
- Математика - әлемде болып жатқан түрлі құбылыстарды, жаңалықтарды дұрыс қабылдап, түсінуге көмектеседі;
Оқушының математикаға ынтасын дамыту мұғалімнің негізгі мақсаты болып табылады. Оқушының пәнге қызығушылығы - оның табысты да, түбегейлі игерудің негізгі шарты.
Пәнге танымдық қызығушылықтиы дамытудың үш шарты бар:
Біріншісі - мазмұнның жаңғыртылуы, бұрын жария етілген фактілерді жаңаша сипаттау, хабарлап отырған материалға тарихи бағдар беру, ілімін практикалық мәнін ашып көрсету және ғылымның соңғы жаңалықтарын, табыстарын жүйелі баяндау;
Екіншісі - өз бетінше жұмыс істеудің әрқилы түрлерін, оқытудың проблемалық тұрғыда қолға алған материалды зерттеу негіздеріне және оқушының шығармашылық, практикалық жұмыстарына бағытталған оқыту тәсілдері;
Үшіншісі - оқуының қабілетін ұштау, мұғалімнің оқушыға көмек беруге дайын тұруы, олардың мүмкіндіктеріне қолдау көрсету қабілеті, талап қоюшылдығы мен адалдығы, балаларды көтермелей білу, сондай - ақ оқушылардың өзара бәсекелесіне көмек көрсете білу қасиеті оқушы назарын аударатын ойына түрткі болатын математика туралы қызғылықты материалдар, әртүрлі тартымды есептар, математикалық софизмдер мен ойындар сабақ үстінде өзінің орнын табу керек. Мұндай есептер оқушыларды математикаға деген ынта ықыласын арттырып, есептерді өздігінен шешуге итермелейді, логикалық ой өрісін дамытады.
Қызғылықты есептер мен математикалық ойындар, әсіресе, бесінші және алтыншы сынып оқушылары үшін пайдалы.
Оқушылар бір сарынды есеп шығарудан шаршамас үшін әртүрлі математикалық жарыстар, ойындар ұйымдастырған жөн.
Әр мұғалімнің негізгі мақсаты - сабақ сапасын көтеру. Оқушылардың сабаққа деген қызығушылығын арттыру, олардың ізденімін, танымын қалыптастыру.
Міне, сондықтан математикалық білімдерін бастауыш сыныптан бастап, орта буыннан бастап дұрыс қалыптастыру керек. Орта буын математикасы бөлшектер түсінігімен басталады. Ал, бұл ұғымды дұрыс меңгеру үшін бастауыш сыныптардағы бөлік ұғымы жақсы меңгерілуі керек. Яғни бастауыш сыныптан келген оқушы бөлшек тақырыбын өту барысында бөлік ұғымын таныс, онымен жұмыс істеуді білулері керек. Ал, бөлшек ұғымын жақсы меңгерген оқушының математикаға деген қабілеті артып, қалған тақырыптарды меңгеруге көмек береді.
Дипломдық жұмыстың мақсаты:
Жай бөлшектер тақырыбын оқушыларға жеткілікті түрде меңгеру, дұрыс қалыптастыру үшін қолданылатын әдіс-тәсілдерді көрсету.
Тақырыптың өзектілігі:
Жай бөлшектер тақырыбын дұрыс меңгеру арқылы математикалық білімді жақмы қалыптастыру.
Дипломдық жұмыстың құрлымы:
Жұмыс кіріспе, негізгі бөлімде теориялық және практикалық бөлім және қорытындыдан тұрады.
Негігі теориялық бөлімде жай бөлшектердің шығу тарихы, әр елдерде жазылуы, мектеп курсында берілетін анықтаалар, бөлшектерге амалдар қолдану туралы жаөылса, екінші практикалық бөлімде мұғалімдердің тәжірибесінен алынған сабақтар конспектісі, факультатив сабақтар конспектілері келтірілген.
Қорытында бөлімі бөлшектер тақырыбының маңызы талданған.
ТАРАУ І. « Жай бөлшектер» тақырыбын оқытудағы дәстүрлі әдістер.
- Жай бөлшектердің пайда болу тарихынан.
Бөлшектер ежелден пайда болған. Ерте кезде адамдарға сауда- саттық олжаны бөлгенде, ұзындықты өлшегенде және түрлі есептеу жұмыстарында бөлшектер мен үлестерді есептеу қажет болған. Алғашында математикада бөлшектерді «сынық сандар» деп атаған. Бөлшектер туралы түсініктің дамуында үш түрлі бөлшектер ұғымы қалыптасқан:
- Бірлік бөлшектер - алымдары 1 болатын бөлшектер.
- Жүйеленген бөлшектер. Жүйеленген бөлшектің алымы кез келген бүтін сан, бөлімі тек 10 санының немесе 60 санының дәрежелері ғана болған.
- Жалпы түрдегі бөлшек. Жалпы түрдегі бөлшектің алымы да, бөлімі де кез келген натурал сан болды.
Бөлшектердің мұндай әртүрлілігі есептеу және өлшеу жұмыстарында көптеген қиындықтар туғызды. Бөлшек ұғымының дамуы ғылым мен сауда - саттық жұмыстары өркендеген елдерде: Мысырда. Вавилонда, Үндістанда және Римде қалыптасты.
Ежелгі Мысырлықтар 2 затты 3 адамға қалай бөлетінін ертеректер білген,
 саны арнайы белгілі болған. Барлық
саны арнайы белгілі болған. Барлық
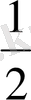 ;
;
 ;
;
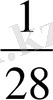 ; бөлшектерді алымында бірлік
; бөлшектерді алымында бірлік
болса, алымында бірлігі жоқ бөлшек египеттерде жалғыз ғана болған. Егер мысырлыққа барлық бөлшекті қолдану керек болса, онда ол негізгі бөлшектердің қосындысы түрінде көрсеткен. Мысалы,
 орнына
орнына
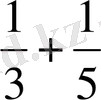
жазатын, кейде бұлай жазу ыңғайлы болатын. Ахмеса папирусында мынадай есеп бар: « 7 нанды 8 адамға бөліп беру». Егер әрбір нанды 8 бөлікке бөлу қажет. Ал Мысырлықша бұл есеп былайша шешіледі:
 бөлшек санын бөліктер түрінде былай жазады:
бөлшек санын бөліктер түрінде былай жазады:
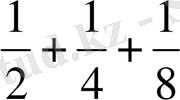 . Яғни әрбір адам үшін жарты нан, төрттен бір
. Яғни әрбір адам үшін жарты нан, төрттен бір
нан, сегізден бір нан беру керек; сондықтан төрт нанды жартыдан, екі нанды төрт бөлікке, ал бір ананды сегіз бөлікке бөлгеннен кейін әр адам өзінің бөлігін ала алады.
Бірақ мұндай бөлшектерді қосу ыңғайсыз болды. Өйткені екі қосылғышқа
бірдей бөліктер енуі мүмкін, сонда қосу кезінде
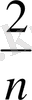 түріндегі бөлшек пайда
түріндегі бөлшек пайда
болады. Ал мысырлықтар мұндай бөлшектердің болуына рұқсат етпеді.
Сондықтан, Ахмеса папирусы
 -ден
-ден
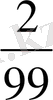 -ға дейінгі бөлшектер қосынды түрінде берілген кестеден басталады. Осы кестенің көмегімен сандарды бөлу орындалады.
-ға дейінгі бөлшектер қосынды түрінде берілген кестеден басталады. Осы кестенің көмегімен сандарды бөлу орындалады.
Мысалы, 5 санын 21 санына бөлу:

Мысырлықтар сонымен қатар бөлшектерді көбейтіп бөлуді де білген. Бірақ көбейту үшін бөліктерді бөліктерге көбейту керек, кейін тағы да кестені пайдалану қажет болды. Бөлу күрделірек болды.
Ежелгі Вавилонда керісінше болды, тұрақты бөлім 60-қа тең еді. вавилондықтардан қалған 60-тық бөлшектерін кейін грек және араб математиктері мен астраномдары пайдаланды. Бірақ онық жүйеде жазылған натурал сандармен және алпыстық бойынша жазылған бөлшек сандармен жұмыс жасау қолайсыз болды. Ал, жай бөлшектермен жұмыс жасау өте күрделі болды. сондықтан голланд математигі Симон Стевин ондық бөлшектергн көшуді ұсынды.
Ежелгі Римде де бөлшектердің қызықты жүйесі болды. Ал асс деп аталатын салмақ бірлігін 12 бөлікке бөлуге негізделген. Он екінші бөлікті асты унция деп атады. Ал, жол, уақыт және тағы басқа да өлшемдерді салмақпен салыстырған. Мысалы, римдіктер жеті уиция жол жүрдім немесебес уиция кітап оқыдым деп айтқан. Бірақ бұл кезде жолдың немесе кітаптың салмағы өлшенгендігі туралы
айтылып тұрған жоқ. Керісінше жолдың
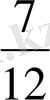 бөлігі жүрілді немесе кітаптың
бөлігі жүрілді немесе кітаптың
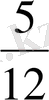
бөлігі оқылғандығы туралы сөз. Ал бөлімі 12 болатын бөлшекті қысқартудан немесе 12 кішкене бөлікке бөлінген бөлшектердің өзінің ерекше аттары болған.
Қазірдің өзінде былай айтылады: Ол бл сұрақты аяғына дейін зерттеп, бірде бір
түсініксіз жері қалмағандығын білдіреді. Бұл сөз Римнің «скрупулезно»
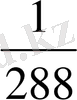
асса- «скрупулус» сөзінен пайда болған. Тағы да мынадай атаулар болған:
«семис»-алтыншы бөлік, «семиунция»- жарты унция, яғни
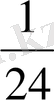 асса т. с. с.
асса т. с. с.
Барлығы 18 әртүрлі бөлшектердің аты болған. Бөлшектермен жұмыс жасау үшін осы бөлшектерді көбейту және қосу ережелерін естерінде сақтау керек
болады. Сондықтан римдік сатушылар триенса (
 асса) және секстанса сандарының қосындысы семис, ал беса (
асса) және секстанса сандарының қосындысы семис, ал беса (
 асса) санын сескунцию (
асса) санын сескунцию (
 унции, т. с. с
унции, т. с. с
 асса) санына көбейткенде унция шығатынын білген. Жұмыстарын жеңілдету үшін олардың кейбіреуі бізге де жеткен арнайы кестелер құрған.
асса) санына көбейткенде унция шығатынын білген. Жұмыстарын жеңілдету үшін олардың кейбіреуі бізге де жеткен арнайы кестелер құрған.
Ертеде әр түрлі елдер бөлшек сандарды белгілеуде өздерінің түрліше
символдарын енгізді. Мысалы, мысырлықтар
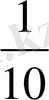 -ді
-ді
 белгісімен,
белгісімен,
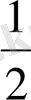 -ді
-ді
 белгісімен және
белгісімен және
 -ді
-ді
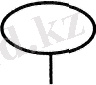 белгісімен көрсеткен. Олар
белгісімен көрсеткен. Олар
 бөлшегін
бөлшегін
арасына қосу таңбасын қоймай
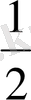
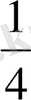
 түрінде жазды. Сол сияқты
түрінде жазды. Сол сияқты
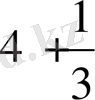 -ді
-ді
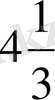
түрінде жазған. Демек, аралас сандарды осылайша ( қосу белгісін жазбай ) жазу сол кезде қалыптасқан.
Ежелгі Үндістанда жай бөлшектерді жазуда бөлшек сызығын сызбай,
алымын үстіне, бөлімін астына жазған. Мысалы,
 -ді
-ді
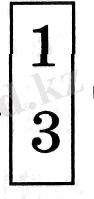 түрінде,
түрінде,
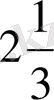 -ді
-ді
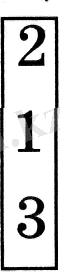 деп немесе
деп немесе
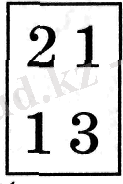 түрінде жазған. Демек, сол кезден бастап бүтін санды бөлімі 1 болатын бөлшек етіп жазу қалыптасқан.
түрінде жазған. Демек, сол кезден бастап бүтін санды бөлімі 1 болатын бөлшек етіп жазу қалыптасқан.
Бөлшекті осы түрде жазу тәжік ғалымы әл-Насавидің (1030 жылдары ) ғылыми жұмыстарында орын алған. Әл-Насави, егер бөлшектің бүтін бөлігі жоқ
болса, оның орнына 0 жазған. Мысалы,
 -ді
-ді
 түрінде жазған. Ежелден
түрінде жазған. Ежелден
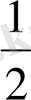 -жарты ;
-жарты ;
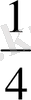 -ді ширек ;
-ді ширек ;
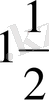 -ді бір жарым және т. с. с. деп атаған. Осылайша
-ді бір жарым және т. с. с. деп атаған. Осылайша
« жарты », « ширек » ұғымдары қалыптасқан.
Бөлшек сызығын уал-Хассара (ХІІ ғасырда) және итальяндық Леонардо Пизанский « бөлшек » деген сөзді енгізген. Бөлшек сызығы ХVІ ғасырда ғана белгілеуге толық енді.
Ертедегі вавилондықтар өздерінің ғылыми есептеу жұмыстарында алпыстық бөлшектерді (бөлімі алпыс саны болатын) пайдаланды. Осыдан қалған бөлшек жүйесінен қазіргі ауқыт бірлігіндегі 60-тық жүйе қалыптасқан. 1мин
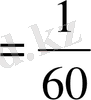 сағ; 1с
сағ; 1с
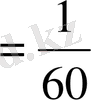 мин. Бөлшектегі «алым», «бөлім» атауларын ХІІІ ғасырда грек математигі Максим Плануд енгізген, жалпы түрдегі
мин. Бөлшектегі «алым», «бөлім» атауларын ХІІІ ғасырда грек математигі Максим Плануд енгізген, жалпы түрдегі
 бөлшегі ежелгі грек ғалымы Архимедтің ( б. з. б. 287-212 ) еңбектерінде пайдаланылаған. ХХ ғасырдың алғашқы жылдарында үнділер бөлшектерге амалдар қолдануды қалыптастырды. Бөлшектер туралы толық мәліметтерді арифметика кітаптарына Орта Азия математигі Әл-Хорезми енгізген.
бөлшегі ежелгі грек ғалымы Архимедтің ( б. з. б. 287-212 ) еңбектерінде пайдаланылаған. ХХ ғасырдың алғашқы жылдарында үнділер бөлшектерге амалдар қолдануды қалыптастырды. Бөлшектер туралы толық мәліметтерді арифметика кітаптарына Орта Азия математигі Әл-Хорезми енгізген.
Бөлшектерді қазіргі алым және бөлім туралы жазылуы Үндістанда ойлап табылған. Тек сол елде алымды - астына, бөлімді -үстіне жазатын болған. Ал, дәл қазіргідей бөлшектердің жазылуын арабтар бастаған.
1. 2. Жай бөлшекке қолданылатын арифметикалық амалдар.
Әр түрлі шамаларды ( ұзындықты, массаны, уақытты) өлшек үшін натурал сандардан басқа бөлшек сандар мен де өлшеуге болады.
1-суретте дөңгелек (тұтас бір дене) тең 4 бөлікке бөлінген. Мұндай тең бөліктер үлестер деп аталады. 1- суреттегі әрбір үлес - дөңгелекті өзара тең 4 бөлікке бөлгендегі 1 бөлігі. Жазылуы дөңгелектің
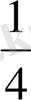 -і;
-і;
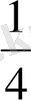 - дің оқылуы: « төрттен бір ». Демек, 1:4 дегеніміз
- дің оқылуы: « төрттен бір ». Демек, 1:4 дегеніміз
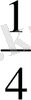 ; 1:4 =
; 1:4 =
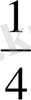 , мұндағы сызықша - бөлшек сызығы.
, мұндағы сызықша - бөлшек сызығы.
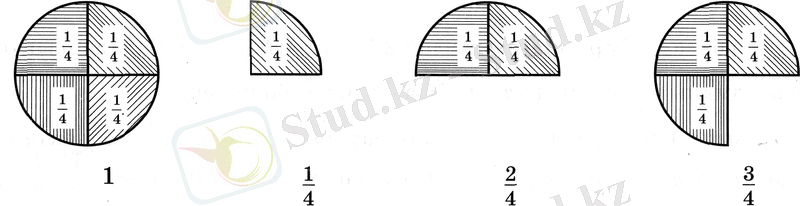
Алдымен бөлшек сызығының астындағы сан шығыс септгігінде оқылады, сонан соң бөлшек сызығының үстіндегі сан атау септігінде оқылады. Егер осындай үлестің (
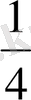 -дің) екеуін алсақ, онда ол
-дің) екеуін алсақ, онда ол
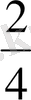 түрінде жазылады. Оқылуы « төрттен екі ». Егер осындай үлестің үшеуін алсақ, онда ол
түрінде жазылады. Оқылуы « төрттен екі ». Егер осындай үлестің үшеуін алсақ, онда ол
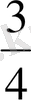 түрінде жазылады. Оқылуы « төрттен үш ». Мұндағы
түрінде жазылады. Оқылуы « төрттен үш ». Мұндағы
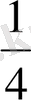 ,
,
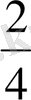 және
және
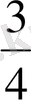 - жай бөлшектер. Жай бөлшектің жалпы түрде әріппен жазылуы:
- жай бөлшектер. Жай бөлшектің жалпы түрде әріппен жазылуы:
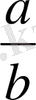 . Мұндағы а- бөлшектің алымы, b-бөлімі.
. Мұндағы а- бөлшектің алымы, b-бөлімі.
Бөлшек сызығының астындағы сан неше үлеске бөлінгенін көрсетеді, сондықтан оны бөлшектің бөлімі деп атайды. Бөлшек сызығының үстіндегі сан неше үлестің алынғанын көрсетеді, сондықтан оны бөлшектің алымы деп атайды.
Кез келген натурал сан бөлшектің бөлімі, ал 0 саны және кез келген натурал сан алымы бола алады.
Мысалы, 2 алманы 3 балаға тең бөліп берсек, олардың әрқайсысы неше бөліктен алма алады?
Шешуі. Алманы әрқайсысын 3 тең бөліккке бөлеміз. Әрбір бөлік алманың
 -і болады. Бір балаға осындай 2 бөліктен беріледі. Балалардың әрқайсысы алманың
-і болады. Бір балаға осындай 2 бөліктен беріледі. Балалардың әрқайсысы алманың
 бөлігін алады.
бөлігін алады.
Алымы 1 саны, бөлімі 1-ден өзге натурал сан болатын бөлшектер бірлік бөлшектер (аликвоттық бөлшектер) деп аталады. Мысалы,
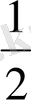 ,
,
 ,
,
 ,
,
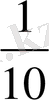 , т. с. с бірлік бөлшектер.
, т. с. с бірлік бөлшектер.
Бір натурал санды екінші натурал санға бөлуді жай бөлшекпен жазуға болады. Бөлінгіш бөлшектің алымына жазылады да, бөлгіш бөлшектің бөліміне жазылады. Демек, бөліндіні жай бөлшек түрінде жазуға болады. Мысалы,
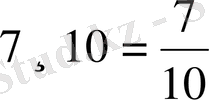
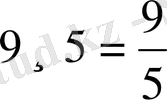
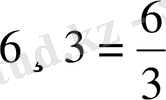 .
.
Натурал санды бөлшек түрінде де жазуға болады. Мысалы,
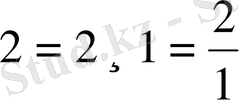 немесе
немесе
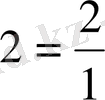 ;
;
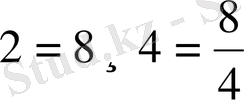 немесе
немесе
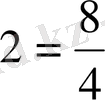
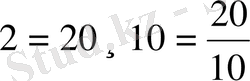 немесе
немесе
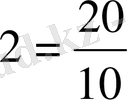 .
.
Әріппен жазсақ:
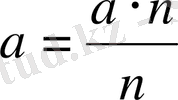 .
.
Мұндағы а- берілген натурал сан, n=1, 2, 3, . . .
Өзара тең бір үш шаманы, мысалы А 1 , А 2 және А 3 үш ұзындықты алайық та, оларды өлшеудің бір ғана бірлігімен - метрмен өлшейік.
Бұл шамалар метрден қысқа. Онда бұл шамаларды өлшеу үшін метрдің өлшенетін ұзындықтың ішінде бүтін сан рет болатын қандай да болса, бір үлесін алуымыз керек болады. А 1 ұзындықты өлшеу үшін метрдің төрттен бір
бөлігін алып, А
1
ұзындықтың
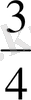 метрге тең екенін анықтадық. Енді әрбір ширек метрді тең 5 бөлікке бөлеміз. Сонда метрдің одан да ұсақ үлесі шығады: мұндай үлестер
метрге тең екенін анықтадық. Енді әрбір ширек метрді тең 5 бөлікке бөлеміз. Сонда метрдің одан да ұсақ үлесі шығады: мұндай үлестер
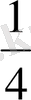 метрде бесеу болады, демек бір бүтінде, яғни 1 метрде олардың саны 5*4=20 болады. Олай болса, бұл метрдің
метрде бесеу болады, демек бір бүтінде, яғни 1 метрде олардың саны 5*4=20 болады. Олай болса, бұл метрдің
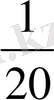 үлесі болады;
үлесі болады;
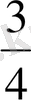 метрде жиырмадан бір (жиырмалық) үлестер 5*3=15 болады.
метрде жиырмадан бір (жиырмалық) үлестер 5*3=15 болады.
Ұзындық А
2
=А
1
, демек, А
2
ұзындық та
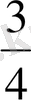 метрге тең, бірақ егер біз бұл ұзындықты ширек мертмен емес, оның жиырмалық үлесімен өлшейтін болсақ, онда А
2
ұзындық
метрге тең, бірақ егер біз бұл ұзындықты ширек мертмен емес, оның жиырмалық үлесімен өлшейтін болсақ, онда А
2
ұзындық
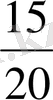 метрге тең екенін анықтаған болар едік. А
1
мен А
2
тең ұзындықтар бір ғана өлшеу бірлігімен (метрмен) өлшенгендіктен,
метрге тең екенін анықтаған болар едік. А
1
мен А
2
тең ұзындықтар бір ғана өлшеу бірлігімен (метрмен) өлшенгендіктен,
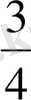 метр
метр
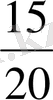 метрге немесе
метрге немесе
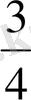 бөлшегі
бөлшегі
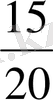 бөлшегіне тең.
бөлшегіне тең.
Әрбір ширек метрді тең 25 бөлікке бөлсек, метрдің неғұрлым ұсақ үлестері шығады,
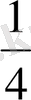 метрде мұндай үлестердің саны 25 болады, демек 1 метрде, яғни 1 бүтінде, олардың саны 25*4=100 болады, демек олардың метрдің жүздік үлестері;
метрде мұндай үлестердің саны 25 болады, демек 1 метрде, яғни 1 бүтінде, олардың саны 25*4=100 болады, демек олардың метрдің жүздік үлестері;
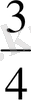 метрде жүздік үлестер 25*3= 75 болады. Ұзындық А
3
= А
1
=
метрде жүздік үлестер 25*3= 75 болады. Ұзындық А
3
= А
1
=
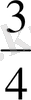 метр болсын. Егер А
3
ұзындықты ширек метрмен ( метрдің төрттен бір үлесімен) емес, оның жүздік үлесімен өлшейтін болсақ, онда А
3
ұзындық
метр болсын. Егер А
3
ұзындықты ширек метрмен ( метрдің төрттен бір үлесімен) емес, оның жүздік үлесімен өлшейтін болсақ, онда А
3
ұзындық
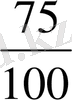 метрге тең екенін таптық. Бұдан
метрге тең екенін таптық. Бұдан
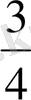 метр
метр
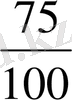 метрге немесе
метрге немесе
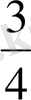 бөлшегі
бөлшегі
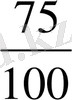 бөлшегіне тең.
бөлшегіне тең.
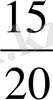 пен
пен
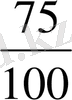 бөлшектерінің де өзара тең екеніне осылайша көз жеткізуге болады.
бөлшектерінің де өзара тең екеніне осылайша көз жеткізуге болады.
Сонымен, бір ғана бірлікпен өлшенген екі шама өз ара тең болса, онда ол шамаларды өрнектейтін бөлшек сандар да өзара тең болады.
Өзара тең
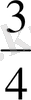 пен
пен
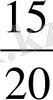 ,
,
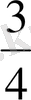 пен
пен
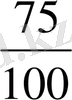 ,
,
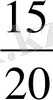 пен
пен
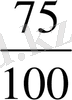 бөлшектерін қос-қостан алып, тең
бөлшектерін қос-қостан алып, тең
бөлшектердің әр қосының қасиеттері бірдей болатындығын, тап айтқанда; бірінші бөлшектің алымы мен екінші бөлшектің бөлімінің көбейтіндісі екінші бөлшектің алымы мен бірінші бөлшектің бөлімінің көбейтіндісіне тең болатындығын көреміз.
Анығында 3*20=15*4; 3*100=75*4; 15*100=75*20. Өзара тең бөлшектердің барлығында да осындай қасиет болады, сондықтан да бұл қасиет бөлшектердің теңдігінің анықтамасы ретінде алынады, атап айтқанда, бұл анықтама былай
айтылады : егер бірінші бөлшектің алымы мен екінші бөлшектің бөлімінің көбейтіндісі, екініші бөлшектің алымы мен бірінші бөлшектің бөлімінің көбейтіндісіне тең болса, онда мұндай екі бөлшек өзара тең деп есептеледі .
Мысалы: егер ab
1
= a
1
b,
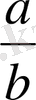 бөлшегі
бөлшегі
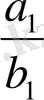 бөлшегіне тең болады.
бөлшегіне тең болады.
Бүтін сандардың теңдігі сияқты бөлшек сандардың теңдіктерінің мынадай негізгі қасиеттері бар:
- рефлексивтік;
- симметриялық;
- транзитивтік.
Бөлшектің алымын да, бөлімін де нольге тең емес бірдей санға көбейтуден немесе бөлуден бөлшектің шамасы өзгермейді.
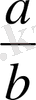 бөлшегі берілсе,
бөлшегі берілсе,
1)
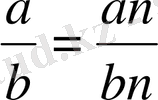 2)
2)
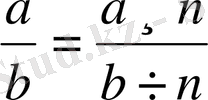
Мысал, Дөңгелекті өзара тең 4 бөлікке бөліп, оның 3 бөлігін бояу қажет (2 сурет) . Сонда дөңгелектің
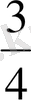 -і боялады. Егер әрбір
-і боялады. Егер әрбір
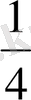 бөлікті тағы да өзара тең 2 бөлікке бөлсек, онда дөңгелектің
бөлікті тағы да өзара тең 2 бөлікке бөлсек, онда дөңгелектің
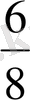 -і боялады.
-і боялады.

Демек,
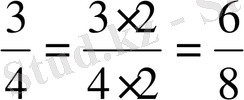 ;
;
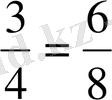 .
.
Сонда
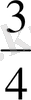 және
және
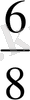 бір санының ( бөлшектің ) түрліше жазылуы.
бір санының ( бөлшектің ) түрліше жазылуы.
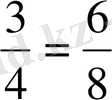 теңдігін
теңдігін
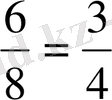 түрінде де жазуға болады. Себебі
түрінде де жазуға болады. Себебі
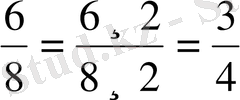 . Осыдан шығатын қорытынды: Жай бөлшектің алымын да, бөлімін де бірдей натурал санға көбейткеннен немесе бөлгеннен жай бөлшек өзгермейді. Бұл - бөлшектің негізгі қасиеті.
. Осыдан шығатын қорытынды: Жай бөлшектің алымын да, бөлімін де бірдей натурал санға көбейткеннен немесе бөлгеннен жай бөлшек өзгермейді. Бұл - бөлшектің негізгі қасиеті.
Бөлшектің қарастырылып өткен бұл қасиетінің бөлшектерді түрлендіруде үлкен маңызы зор, сондықтан ол- бөлшектің негізгі немесе басты қасиеті деп аталады.
Бөлшектерді қысқарту және бөлшектерді ортақ бөлімге келтіру осы қасиетке негізделген.
Бөлшектерді қысқарту және оларды ең кіші ортақ бөлімге келтіру.
Бөлшектің алымы мен бөліміндегі олардың ортақ көбейткіштерін, бөлшектің мүшелерін осы көбейткіштерге бөлу арқылы жоюды, яғни
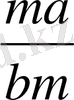 бөлшегін
бөлшегін
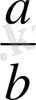 бөлшегімен алмастыруды бөлшекті қысқарту деп атайды.
бөлшегімен алмастыруды бөлшекті қысқарту деп атайды.
Бұл сияқты алмастыруды орындауға болады, өйткені бөлшктің алымын да, бөлімін де бірдей санға бөлуден оның шамасы өзгермейді.
Әрбір бөлшектің қысқартылмайтын түрі деп аталатын бір ең жай түрі болу керектігі өзінен-өзі түсінікті. Бөлшектің қысқартылмайтын түрін шығарып алу үшін бөлшектің алымын да, бөлімін де олардың ең үлкен ортақ бөлгішіне бөлу керек. Қысқартылмайтын бөлшектің алымы мен бөлімі өзара жай сандар болады.
Бөлшектерді қысқартудың екі тәсілі.
1. Біртіндеп қысқарту. Сандардың бөлінгіштік белгілерін пайдаланып, бөлшектің алымын да, бөлімін де олардың ортақ бөлгішіне біртіндеп бөледі.
Мысалы.
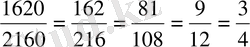 .
.
2. Толық қысқарту. Бөлшектің алымы мен бөлімінің ең үлкен ортақ бөлгішін табады да, осыған бөлшектің мүшелерін бөледі.
Екінші тәсіл, әдетте, бөлшектің мүшелерінің ортақ бөлгіштерін бөлгіштік белгілері бойынша табу қиын болған жағдайларда қолданылады.
Мысал:
 .
.
Бөлшектің 2 177 мен 1 555 мүшелерінің ең үлкен ортақ бөлшегін біртіндеп бөлу жолымен табамыз.

Демек, Евклид алгоритмі бойынша (2177; 1555) =311
Сонымен
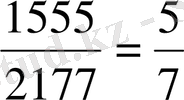
Көрнекі болу үшін бөлшектің үстіңгі жағына оны қысқартатын санды жазуымызға болады, бірақ оны әдетте жазбайды:
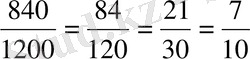 .
.
Берілген бірнеше бөлшектерді ортақ бөлімге келтіру деп осы бөлшектерді шамаларын өзгертпей бөлімдері бірдей боларлықтай етіп, түрлендіруді айтады.
Бұл үшін барлық бөлімдердің еселік саны берілген бөлшектердің ортақ бөлімі етіп алып, әр бөлшектің алымын да, бөлімін де бөлімінің табылған еселікке жетпей тұрған көбейткішіне көбейтсе болғаны.
Мысалы:
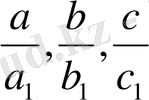 бөлшектерін былайша жазуға болады.
бөлшектерін былайша жазуға болады.
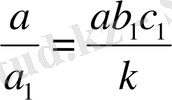 ,
,
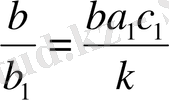 ,
,
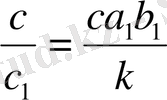 ,
,
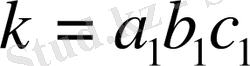
Бұл бөлшектің әрқайсысын түрлендірудің мәнін бөлшектің алымын да, бөлімін де бірдей анға көбейтуде екендігі өзінен-өзі түсінікті; бұдан бөлшектің шамасы өзгермейді (бөлшектің негізгі қасиеті бойынша) .
Бөлшектерге амалдар қолданғанда есептеуді оңай ету және ықшамдау мақсатымен оларды ең кіші ортақ еселігі осы бөлшектердің ең кіші ортақ бөлімі болып табылады.
Берілген бөлшектерді ең кіші ортақ бөлімге келтіру үшін, егер мүмкін болса, әуелі оларды қысқартады, одан кейін барлық бөлімдердің Е. К. О. Е. табады, әр бөлім үшін тиісті толықтауыш көбейткішін анықтайды да, бөлшектің екі мүшесін де осы көбейткішке көбейтеді.
Бөлшектерді ең кіші ортақ бөлімге келтірудің дербес жағдайлары.
1-жағдай. Бөлімдердің ешбір қосының ортақ көбейткіштері болмайды.
Бұл жағдайда бөлімдердің барлығы да өзара жай сандар болатындығы өзінен-өзі түсінікті. Мұндай сандардың ең кіші ортақ еселігі олардың көбейтіндісіне тең. Олай болса, бұл қарастырылып отырған жағдайда бөлшектерді ең кіші ортақ бөлімге келтіру үшін әр бөлшектің екі мүшесін де қалған бөлшектердің бөлімдерінің көбейтдісіне көбейтсе болғаны.
Мысалы:
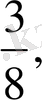
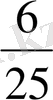 ,
,
 . Бөлімдердің Е. К. О. Е
. Бөлімдердің Е. К. О. Е
 -ге тең.
-ге тең.
8-дің толықтауыш көбейткіші 75-ке тең.
25-тің толықтауыш көбейткіші 24-ке тең.
3-тің толықтауыш көбейткіші 200-ге тең.
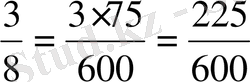 ;
;
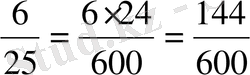 ;
;
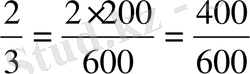 .
.
2-жағдай. Қысқартылмайтын бөлшектердің бөлімдерінің ең үлкені былайғы бөлімдердің әрқайсысына бөлінеді.
Бұл жағдайда ең үлкен бөлім барлық бөлімдердің ең кіші ортақ еселігі болады; ендеше ол берілген бөлшектердің ең кіші ортақ бөлімі де болып табылады.
Мысалы:
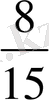 ,
,
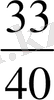 ,
,
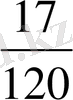 бөлшектерін ең кіші ортақ бөлімге келтіру керек.
бөлшектерін ең кіші ортақ бөлімге келтіру керек.
m (15; 40; 120) =120
15-тің толықтауыш көбейткіші 8-ге тең.
40-тың толықтауыш көбейткіші 3-ке тең.
Сонымен,
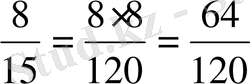 ;
;
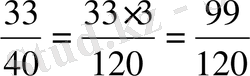 және
және
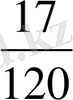 .
.
Бөлшектердің ортақ бөлімге келтіруінің дұрыстығын бөлшектерді қысқарту арқылы тексеріледі; бөлшектердің қысқартулуының дұрыстығы қысқарған бөлшекті бастапқы бөлшекпен ортақ бөлімге келтіру арқылы тексеріледі.
Бөлшектерді салыстыру.
Бөлшектерді натурал сандар сияқты салыстырылады.
Егер
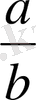 бөлшегінің алымының
бөлшегінің алымының
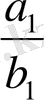 бөлшегінің бөліміне көбейтіндісі екінші бөлшектің алымының біріншісінің бөліміне көбейтіндісінен артық, яғни
бөлшегінің бөліміне көбейтіндісі екінші бөлшектің алымының біріншісінің бөліміне көбейтіндісінен артық, яғни
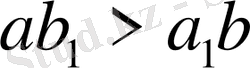 болса, онда
болса, онда
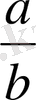 бөлшегі
бөлшегі
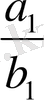 бөлшегінен үлкен болады.
бөлшегінен үлкен болады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz