Теріс Сандар арифмет

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 22 бет
Таңдаулыға:

Рационал сандар жиыны
Мазмұны

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... ... ... ...3
1. Рационал сандар туралы жалпы түсінік
1.1 Оң және теріс
сандар ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ...5
1.2 Рационал сандардың шығуы және оның даму
тарихы ... ... ... ... ... ... ... . ...10
2. Рационал сандарға арналған сабақ жоспарлары
2.1 Рационал сандарға амалдар қолдану
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .15
2.2 Оң және теріс сандарға амалдар
қолдану ... ... ... ... ... ... ... ... ... ... ... ... ... ..18
2.3 Рационал сандарды көбейту
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 22

Қорытынды ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... ..25
Пайдаланған әдебиеттер
тізімі ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ..27

Кіріспе
Сан — математиканың негізгі ұғымдарының бірі. Қарапайым түрде алғашқы
қоғамдарда-ақ пайда болған, кейін бірте-бірте қолданыс аясы кеңейіп әрі
жалпыланды. Кейбір заттарды санауға байланысты бүтін оң (натурал) Сан дар
ұғымы, кейіннен Сандардың натурал қатарының (1, 2, 3, 4, ...) шексіздігі
туралы идея пайда болды. Сан ұғымының алғашқы кеңеюі — натурал Сандарға
бөлшек Сандардың қосылуы болды. Ол ұзындықты өлшеу, ауданды табу, сондай-
ақ, атаулы шамалардың үлесін бөліп шығару қажеттілігіне байланысты
қолданысқа енгізілді. Теріс Сандар арифмет. есептерді шешудің жалпы
тәсілдерін беретін алгебраның ғылым ретінде дамуына байланысты шықты.
Бүтін, бөлшек (оң және теріс) және нөл сандары рационал сан деп аталды.
Айнымалы шамалардың шексіз өзгеруін зерттеу үшін Сан ұғымы кеңейтіліп,
нақты сандар жиынтығы пайда болды. Шамалардың қатынасын (мыс., квадрат
диагоналының оның қабырғасына қатынасы) дәл өрнектеу қажеттігі иррационал
сандар ұғымын енгізуге себепші болды. 16 ғ-да квадрат және куб теңдеулерді
шешуге байланысты жорымал сандар ұғымы енгізілді. Сан ұғымы дамуының соңғы
кезеңі комплекс Сандардың енгізілуі болды. Бұл идея 16 ғ-да 3- және 4-
дәрежелі алгебр. теңдеулердің шешімін табуға байланысты пайда болған.
Натурал сандар нәрселерді санау нәтижесінде пайда болғандағы
мәлім. Адамға шамаларды өлшеу қажет болғандығының және өлшеу
нәтижесі әр дайым бүтін сандармен өрнектеле бермейтігінің салдарынан
натурал жиынтығын ұлғайтуға тура келеді.
Сан ұғымының тарихи даму процесі мұнымен аяқталмайды.Алайда сан
ұғымының ұлғайуына әр дайым алғашқы түрткі болып табылған жағдай
адамдардың тек практикалық қажеті ғана емес еді. Математикалық өз
міндет-мақсаттары сан ұғымының ұлғайуын талап еткен жағдайларда
болған. Теріс сандар ұғымы алгебралық теңдеулерді шешу практикасында
пайда болды.
Натурал сандар жиынын бөлшек сандарға жеткізе ұлғайтқаннан
кейін кез-келген бүтін санды басқа бір бүтіннен азайту көпке дейін
мүмкін емес болып көрінеді. Алайда теңдеулерді шешкенде аз саннан
көп санды азайтуға тура келетін жағдай жиі кездесетін, сондықтан
теріс сан ұғымына талап болуға тура келетін.
Сан әуел баста заттарды санаудың қажеттілігінен туған
математикалы ұғымдардың бірі. Кейін ол математикалық білімнің дамуына қарай
жетілдірілді. Бұл ұғым өте ерте заманда адамдардың практикалық
қызметтерінінен қажеттілігінен келіп туды. Нәрселерді санауда
пайдаланылатын сандарды натурал сандар деп аталады. Натурал сандар қатары 1
санынан басталады.Оның мүшелері шексіз болады. Натурал сандар ұғымының
дамуы ерте заманда адамдардың заттар жиынтығының санын оларды санамай-ақ ,
яғни өзара бірмәнді сәйкестікті тағайындау негізінде қабылдануымен
сипатталады.
Уақыт өте келе адамдар сандарды атауды ғана емес, сонымен қатар оларды
белгілеуді де, сондай-ақ олармен амалдар қолдануды да үйренді.
Натурал сан терминін тұнғыш рет римдік ғалым А. Боэций (шамамен 480-514
жылдар) қолданған. Натурал сан ұғымы қалыптасқаннан кейін сандар дербес
объектлерге айналды.
ХІХ ғасырда ғалымдардың назары натурал сандармен есептеулер жұргізуге
негіз болған теорияларды құруға және логикалық тұрғыдан негіздеуге
аударылды. Натурал сандар ұғымының өте қарапайым және табиғи көрінетіні
сондай, ғылымда ұзақ уақыт бойы оны қандай да болсын қарапайым ұғымның
терминдерімен анықтау туралы мәселе қойылған жоқ.

1. Рационал сандар туралы жалпы түсінік
1.1 Оң және теріс сандар
Оң сан - нөлден үлкен (a0) нақты сан(a). Оң сандар - сан түзуінің
бойында санақ бас нүктесінің оң жағында (яғни нөлдің оң жағында) жататын
нүктелермен бейнелененеді.
XVII ғасырда математика, механика, астрономия кең өрістеп
дамыды.Теріс сандарды қолдану нәтижесінде математикалық есептеу
жұмысы едәуір жеңілденді де, ол сандардың математикадағы мәні
барған сайын арта түсті. XVII ғасырдың 20-шы жылдарының өзінде
Стевин шәкірті,фламанд математигі А. Жирар теңдеулерді шешкенде теріс
шешімдерді де ескеріп отырды және теріс сандарды оң сандармен
қатар пайдаланды.
Француз математигі, физигі, философы Декарттың 1637 жылы басылып
шыққан Геометрия деген атақты шығармасында оң сандар мен теріс
сандардың геометриялық түсініктемесі баяндалады; оң сандар сан осінің
бойында, бас нүкте нольдің (0) оң жағында жатқан нүктелермен, ал
теріс сандар нольдің сол жағында жатқан нүктелермен кескінделеді.

Оң және теріс сандарға геометриялық түсініктеме беру теріс
сандар табиғатын айқынырақ түсінуге және олардың барлығын мойындауға
септігін тигізді. Теңдеулердің оң және теріс шешімдерін қарама-қарсы
бағытталған кесінділермен кескіндеп көрсетуі арқылы Декарт бұл
шешімдерді тең праволы, бірдей нақтылы деп есептейтіндігін әйгілейді,
бірақ сонда да дәстүр бойынша олардың біреулерін ақиқат,екінші
біреулерін жалған деп бұрынғыша атай берді.
Алайда, теріс сандарды көбейту және бөлу ережелері әлі де
сипатталып негізделмегендіктен, тіпті XVIII ғасырдың өзінде ғалымдардың
теріс сандарды да, оң сандар сияқты, өздігінше бар сандар деп
тану жөніндегі таласы аяқтала қойған жоқ еді. Теріс сандарды
осылайша танып мойындауды, атап айтқанда, Ньютон, Эйлер және ол
кездегі орыс математиктерінің барлығы дерлік жақтады. Теріс сандарды
жұрт XIX – ғасырдың бірінші жартысында оң және теріс бүтін
сандардың дәйекті қатаң теориясы дамыған кезде жаппай танып
мойындады.
Теріс сан - нөлден кіші нақты сан.Теріс сан - сан өсінде санақтың бас
нүктесінің сол жағында, яғни нөлдің сол жағында орналасқан нүктелермен
белгіленген.Көне заманнан белгілі натурал сандар математиктерді кейбір
жағдайларда тұйыққа тіреген.Алғашында кіші сандарды үлкен сандарға бөлу
амалы, кейіннен кіші саннан үлкен санды шегеру мәселесі туындаған.Кіші
санды үлкен санға бөлу амалы орындалу үшін бөлшек сандар ұғымы, соңынан
кіші саннан үлкен санды шегеру теріс сандар ұғымын енгізумен біржолата
шешілген.Теріс сан ұғымы алғашқы кездері біздің заманымыздың VII ғасырында
Үнді елінің математиктерінің ойын мазалаған.Олар кіші саннан үлкен санды
шегеру мәселесін сауда-саттықта қолданылатын қарыз(борыш) ұғымымен
ұштастыру нәтижесінде жаңа ұғым - теріс сан ұғымын қалыптастырған.Сауда-
саттық ісіндегі қарыз(борыш) мәселесі кіші саннан үлкен санды шегерудің
түпқазығы іспеттес болды.Үнді математиктері кіші саннан ұлкен санды
шегеруді мысалы, 3 - 5 айырымы түрінде есептемеген, керісінше 5 - 3 айырымы
түрінде азайтып, нәтижесін "қарыз"("борыш"), яғни берешек пұл немесе
басқадай зат деп түсіндірген.Осылайша есептеу негізінде қосу және азайту
амалын орындау мүмкін болғанымен көбейту және бөлу ережелерін түсіндіру
мүмкін болмаған.
Кіші саннан үлкен санды шегерудің мүмкін болмауы математик ғалымдардың
натурал сандар қатарының бір бағытта ғана шексіз математик ғалымдардың
натурал сандар қатарының бір бағытта ғана шексіз болуынан деп жорымалдауына
негіз болған.Мысалы, 7, 6, 5, 4, 3, 2, 1 натурал сан қатарынан 1 санын
шегеретін болсақ: 6, 5, 4, 3, 2, 1 сандар қатарының пайда болатындығына
ешкімнің күмәні жоқ.Осылайша 1 санын шегеруді жалғастыра берсек, ең соңында
шегерілетін сан "жоқ" санды да "сан" деп есептеуіміз қажет екеніне ешкімнің
күмәні болмаса керек.Кейіннен осы "жоқ" санның "нөл"(латынша нуллис -
"ешқандай" деген сөзінен қалыптасқан) деп аталып кеткенін
білеміз.Нөлден(яғни нөл санынан) 1 санын шегеру мүмкін болады деп есептеліп
бұл айырым: - 1(минус 1) болып белгіленіп кетті.Осылайша жаңа сандар
тізбегі, -1, -2, -3, ... . қолданысқа енген.Осы сандар бүтін теріс сандар
деп аталған.Осылардың алдында тұрған минус таңбасы теріс санның 1 санынан
шегеруден пайда болғанын меңзейді.Сондықтан бұл белгі "мөлшер белгісі" деп
аталған.Сырт түрі - болып жазылатын "минус" белгісі азайту амалында
"амал белгісі" деп аталды.
Бүтін теріс сан ұғымы енгізілгеннен кейін, оның соңынан бөлшек теріс
сандар ұғымы қалыптасқан.Арифметикада теріс сандарға қарама-қарсы оң
сандардың қолданылатынын білеміз.Оң сандар(бүтін және бөлшек) және теріс
сандар(бүтін және бөлшек) нөл санымен қоса - рационал сандар деп аталады.
Мысырлықтармен вавилондықтар түгіл, ежелгі гректерде теріс
сандарды білмеген. Теріс сан ұғымы сызықтық теңдеулер системасын
шешкенде пайда болады.Есептеп шығару жұмысымен шұғылданғанда ол
кездегі математиктер есептеу тақтасымен шұғылданған, ал бұл тақтада
сандар есептеу таяқшалары арқылы кескінделген. Ол уақытта + және –
таңбалары болмағандықтан, оң сандарды қызыл түсті таяқшалармен, ал
теріс сандарды қара таяқшалармен кескіндеп көрсеткен. Теріс сандарды
көп уақыт бойы “борыш” ,“кемшін” мағынасындағы сөздермен атаған. Тіпті
VII ғасырдың өзінде Үндістанда оң сандарды мүлік, теріс сандарды
борыш ретінде қарастырған, оларға амалдар қолдана білген.
Арифметикалық есептеулер жүргізу, теңдеулер шешу, алгоритмдер
жасау барысында Қытай математиктері математика тарихында тұңғыш рет
теріс сандар ұғымын енгізді. Олар теңдеудің оң, теріс
коэффиценттерін және сандардың оң, терісін ажырату үшін әр түрлі
таяқшалар мен таңбалар пайдаланған. Қытай математиктері теріс
сандарды қосу, азайтудың қарапайым ережелерін тағайындады.
Математикаға теріс таңбаны енгізу және оларға амалдар қолдану
ережесін тағайындау жалпы сандар жөніндегі ілімнің қалыптасуына мол
үлесін қосты. Қазір теріс сандар бүтін сандардың бір бөлігі.
Диофанттан Бхаскараға дейін. Ежелгі грек математигі Диофант ІІІ
ғасырдың өзінде-ақ мынадай түрлендіруде: (4х-3)(2х-3)=4х-12х+9 теріс
сандарды көбейту ережесімен іс жүзінде пайдаланған болатын.
Алайда Диофант -3-ті жеке бір дербес сан деп қарастырмай, тек
азайтқыш деп,ал кез-келген оң санды қосылғыш деп қана қарастырған.
Көбейту ережесін ол былайша тұжырымдады: Қосылғышқа көбейтілген
азайтқыш нәтижесі азайтқыш; азайтқышты азайтқышқа көбейткенде қосылғыш
шығады. Дербес теріс сандардың болатындығын Диофант мойындамаған,
ал теңдеулерді шешкенде теріс шешім шықса, оны жарамсыз деп біліп,
ескермейтін. Біздің эрамыздың VII ғасырында өмір сүрген үнді
математигі Брахмагупта баяндаған қосу және азайту ережелері
мынандай:
Қәзіргіше Брахмагупта
жазу ережелері
1. а+в=с Екі мүліктің қосындысы мүлік.
2. (-а)+(-в)=-с Екі борыштың қосындысы борыш.
3. а+(-в)=а-в Мүлік пен борыштың қосындысы олардың
айырмасына тең.
4. а+(-а)=0 Мүлік пен оған тең борыштың қосындысы нольге
тең.
5. 0+(-а)=-а Ноль мен борыштың қосындысы борыш борыш
болады.
6. 0+а=а Ноль мен мүліктің қосындысы мүлік мүлік
болады.
7. 0-(-а)=а Нольден азайтылған борыш мүлікке айналады.
8. 0-а=-а Нольден азайтылған мүлік борышқа айналады.

Үнді математигі Бхаскара көбейту және бөлу ережелерін былайша
тұжырымдаған: Екі мүліктің немесе екі борыштың көбейтіндісі мүлік
болады; мүліктің борышқа көбейтіндісі зиян болады.Бұл ереже бөлуге
де қолданылады. Алайда, есептерді теңдеулер құру арқылы шығарғанда
теріс сандар кеңінен пайдаланылып отырғанына қарамастан, Үндістанда
теріс сандарды ерекше бір,онша нақты деуге келмейтін сандар деп
есептеп, оларға азды-көпті күмәндана қараған. Европалық математиктер
де теріс сандарды көп уақытқа дейін мақұлдамады, өйткені олар бұл
сандарды мүлік-борыш деп түсінуге таңырқай да күмәндана қарады.
Расында да, мүліктерді, борыштарды қосуға немесе азайтуға болар, ал
мүлікті борышқа көбейтудің немесе бөлудің қандай нақты мағынасы
болмақ. Міне сондықтан да теріс сандардың математика саласында
тиісті орнын алуы өте қиын болды.

1.2 Рационал сандардың шығуы және оның даму тарихы
Карл Гаусс математиканың сан салаларына сарапқа сала келіп
арифметиканы математиканың патшасы деп бағалаған. Ал арифметиканың негізгі
ұғымы – сан. Ендеше , сол сан ұғымының қалай пайда болуын ашу , білу –
ғылыми методологиялық үлкен мәселе.
Сан туралы ұғым адамзат мәдениетінің тууымен және оның дамуымен тығыз
байланысты. Шынында , егер осы ұғым болмаса , өзіміздің рухани өміріміз бен
практикалық қызметімізді тиісті дәрежеде көрсете алмас едік. Есеп – қисап
жүргізу , уақыт пен қашықтықты өлшеу , еңбек нәтижесінің қорытындысын
есептеу сан ұғымынсыз мүмкін емес.
Жалпы алғанда сан ұғымы басқа ешқандай емес тек шындық дүниеден шыққан
. Өте ерте заманда пайда болған сан ұғымы көптеген ғасырлар бойы
жалпыланып, кеңейе түсті . Сонда сан жайындағы түсініктер адамзаттың
практикалық мұқтаждығына, мәселен, шамаларды өлшеудің қажеттілігіне және
математиканың өзінің ішкі мұқтаждығына байланысты кеңейіп отырғандығы
байқалады. Мысалы шамаларды дәлірек өлшеудің мұқтаждығы оң бөлшек ұғымының
тууына себепті болса, теңдеулерді шешу тәжірибелері мен осы санаудағы
теориялық зерттеулерге байланысты теріс сандар пайда болды. Бастапқыда
санның жоқ екенін белгілеу үшін қолданылған нөл саны теріс сандар
енгізілгеннен кейін сан ретінде қарастырылатын болды.
Француз математигі Рене Декарт (1596-1650) 1637 жылы координаталық
түзуді енгізіп теріс және оң сандарға түсінік берді.
Нөл саны , натурал сандар және оған қарама –қарсы сандар бүтін сандар
жиынын құрайды. Оны Z әріпімен белгілейді. Ал бүтін сандар жиыны және теріс
бөлшектер рационал сандар жиынын құрайды. Рационал сандар жиынын Q әріпімен
белгілейді. Рационал термині латын тіліндегі ratio деген сөзден шыққан.
Ол қазақшаға аударғанда бөлінді , қатынас деген мағынаны береді.Яғни
бұл жерде рационал сан бүтін сандардың қатынасы деп түсіндіріледі. Мысалы
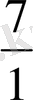7=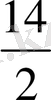;7=; 7=
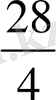
Бұлар бөлшек сандар. Жалпы рационал сан ұғымы әртүрлі шамаларды –
ұзындықты , салмақты . ауданды, перимеитрді және тағы сол сияқты өлшеу
процесіне байланысты пайда болды.
Бөлшектердің пайда болуы шамаларды өлшеумен пайда болды. Ерте кезде
адамдарға сауда – саттық және түрлі есептеу жұмыстарында бөлшектер мен
үлестерді есептеу қажет болған. Алғашында математикада бөлшектерді сынық
сандар деп атаған. Бөлшектер туралы түсініктің дамуында үш түрлі бөлшектер
ұғымы қалыптасқан.
Бірлік бөлшектер – алымдары 1 болатын бөлшектер.
Жүйеленген бөлшектер. Жүйеленген бөлшектің алымы кез келген бүтін сан,
бөлімі тек 10 санының немесе 60 санының дәрежелері ғана болған.
Жалпы түрдегі бөлшек. Жалпы түрдегі бөлшектің алымы да , бөлімі де кез
келген натурал сан болды.
Бөлшектердің мұндай әртүрлілігі есептеу және өлшеу жұмыстарында
көптеген қиындықтар туғызды.Бөлшек ұғымының дамуы ғылым мен сауда-саттық
жұмыстарында өркендеген елдерде: Мысырда , Вавилонда, Үндістанда және Римде
қалыптасты. Ертеде әртүрлі елдер бөлшек сандарды белгілеуде өздерінің
түрліше символдарын енгізді. Мысалы, мысырлықтар 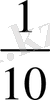-ді -белгісімен,
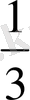-ні-- белгісімен және–ді -белгісімен көрсеткен. Ежелгі
Үндістанда жай бөлшектерді жазуда оның бөлшек сызығын сызбай, алымын
үстіне , бөлімін астына жазған. Мысалы, 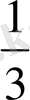-ді түріндежазған.
Бөлшекті осы түрде жазу тәжік ғалымы әл-Насави (1030 жылдар) ғылыми
жұмыстарында орын алған. Ежелден -ді жарты, -ді ширек , 1 -
ді бір жарым және т.с.с, деп атаған. Осылайша жарты , ширек ұғымдары
қалыптасқан.
Бөлшек сызығын уал-Хасара және итальяндық Леонардо Пизанский өздерінің
жазба есептеулерінде пайдаланған. Леонардо Пизанский бөлшек деген сөзді
енгізді.Бөлшек сызығы ХҮІ ғасырда ғана белгілеуге толық неді.
Ертедегі вавилондықтар өздерінің ғылыми зерттеулерінде алпыстық
бөлшектерді (бөлімі алпыс болатын сан) пайдаланылады. Осыдан қалған бөлшек
жүйесінен қазіргі уақыт бірлігіндегі 60-тық жүйе қалыптасқан.
1 мин = 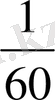сағ; 1сек = 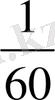мин. Бөлшектегі алым , бөлім
атауларын ХІІІ ғасырда грек математигі Максим Плаунд енгізген, жалпы
түрдегі 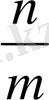бөлшегі ежелгі грек ғалымы Архимедтің еңбектерінде
пайдаланылған. ХХ ғасырдың алғашқы жылдарында үнділер жай бөлшектерге
амалдар қолдануды қалыптастырды.
Самарқанд қаласындағы астрономиялық обсерваторияның негізін салушы әл-
каши бөлшек сандарды жазудың барлық түрлендірулер мен есептеулерін
айтарлықтай ықшамдайтын түрін, яғни ондық бөлшек деп аталатын жаңа түрін
ашты.
ХҮІІ ғасырдың басында ондық бөлшекті жазуды, айыру таңбасы ретінде
үтір немесе нүкте қолданыла бастады.
Ондық бөлшектерді есептеу натурал сандарды есептеуге ұқсас және
ыңғайлы болғандықтан,ғылымдағы,өндірістегі, күнделікті өмірдегі
есептеулерге жиі пайдаланылады. Ондық бөлшектер және ондық бөлшектерге
амалдар қолдану туралы ортаазиялық ғалым Әл-Каши өзінің Арифметика кілті
(1437ж) атты кітабында жазды. Әл-Каши ондық бөлшектерді жазуда үтірді
пайдаланбаған, бірақ ол үтірдің орнына тік сызық қойған. Ал, индерландиялық
математик Стевин Симон (1548-1620) өзінің ондық бөлшек туралы Ондық атты
(1585) кітабында үтірді пайдаланбай , бөлшектің бүтін бөлігі мен бөлшек
бөлігін бір қатарға үтірсіз жазған. Мысалы, 37,48 ондық бөлшегін мына түрде
жазған: 37 0 4 1 8 2. Үтірдің орнына бірліктің үстіне нөл жазған. 1, 2, 3,
... цифрларымен ондық таңбалардың ретін белгілеген.
Өмірде, тұрмыста, кездесетін көптегшен шамалар ( жылдамдық,
биіктік, температура, баға, т.б.) көбейіп, азайып өзгеріп отырады.
Шамалардың өзгерістерін белгілеу үшін оң сандармен қатар теріс сандар
енгізілді. Теріс сандар туралы ең алғашқы ұғым біздің заманымызға дейінгі
ІІ ғасырдағы қытай математиктерінің еңбектерінде кездескен. Оң санды өсу
өзгерісінде қолданса , теріс санды кему ретінде қолданған немесе теріс
сандар қарыз мағынасында қолданса , оң сандарды қолда бар зат мүлік деп
түсінген.
Кейбір шамалардың тура мағынасы,тура бағыты болумен қатар,
қарама- қарсы мағынасы ,қарма –қарсы бағыты болады. Шамалардың өзгерісінің
сан мәнін жазғанда,оқығанда оның тура мағынасының сан мәнінің алдына +
таңбасы қойылады. Шаманың қарама-қарсы мағынасының сан мәнінің алдына -
таңбасы қойылады. Координаталық түзудегі оң (оңға қарай) бағытқа қарама-
қарсы (солға қарай) бағыт теріс бағыт деп аталып, ол бағытта теріс сандар
кескінделеді. Бір-бірінен тек қана таңбаларымен ажыратылатын сандар қарама-
қарсы сандар деп аталады.
Математикаға теріс сандардың енгізілуімен қатар нөл саны да жаңа
мағынаға ие болды. Нөл саны санақ басы болып және қарама-қарсы сандардың
қосындысы деп есептелді. Үнділер нөлді сунья (қазақша бос деген
мағынаны білдіреді) деп атаған, ал арабтар ас-сифр деп аударған,
сондықтан ХҮІІ ғасырға дейін нөл цифр деп аталып келген .
Нөл қазақшаға аударғанда ешқандай дегенді білдіретін латынның
nullus деген сөзінен шыққан.
Қазіргі кездердегі түсінігімізше нөл – сан. Оны басқа сандар
сияқты қосуға,азайтуға , көбейтуге, бөлуге болады , тек қана 0-ге санды
бөлуге болмайды.
Нөл саны координаталық түзуде санақ басы болатын О нүктесінің
координатасы,0 ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.