Сызықты кеңістіктер. Сызықты кеңістіктің базисі мен өлшемі. Сызықты кеңістіктердің изоморфтылығы

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:

Қазақстан Республикасының Білім және ғылым министрлігі.

Ы. Алтынсарин атындағы Арқалық мемлекеттік педагогикалық

институты.

Жаратылыстану және ақпараттандыру факультеті.

Тақырыбы: Сызықты кеңістіктер. Сызықты кеңістіктің

базисі мен өлшемі.

Сызықты кеңістіктердің изоморфтылығы.

Орындаған: И - 21 тобының студенті

Қыдырбекова А.

Тексерген: Сабитбекова Г. С.

Арқалық, 2008 жыл.

Сызықты кеңістіктер.

Сызықты кеңістіктің анықтамасы.

Осы курстың І-бөліміндс (аналитикалык геометрия) векторды векторға қосу және санды векторға көбейту амалдарын қарастырдық. Осы амалдарға орындалатын қасиеттермен таныстық. Ал ІІ-бөлімнің I тарауында бірден ретті матрицаны матрицаға қосу және матрицаны санға көбейту амалдарын қарастырып, осы амалдарға орындалатын қасиеттердіц векторға орындалатын қасиеттермен бірдей екендігін байқадық. Енді осы тарауда сызықты кеңістікте орындалатын амалдарға да жоғарыдағы қасиеттер орындалатынын қарастырамыз. Ол үшін жиын туралы ұғым алайық.

Әртүрлі заттарды біріктіріп оларды бір бүтін зат ретінде қарастыруымызға болады. Осы жаңа зат жиын , ал оның кұрамындағы әртүрлі заттар жиынның элементтері деп аталады. Біз қарастыратын тарауда жиынның элементтерін х, у, z, . . . - кіші латын әріптерімен, ал жиынның өзін бас латын әріптерімсн және сандарды кіші грек әріптерімен белгілейтін боламыз. Мысалы: X - жиын, ал х, у, z, . . . немесе х1, х2 . . . осы жиынның элементтері. х -элемент X жиыннын элементі болатынын (болмайтынын) былай белгілейміз

\[{\tilde{\sigma}}\in G\]

(

\[{\tilde{O}}\in O\]

немесе және

\[{\tilde{\sigma}}{\tilde{\mathrm{e}}}{\tilde{D}}\]

ол х элемент X жиынының элементі немесе х элемент X жиынына тиісті (х элемент X жиынына тиісті емес немесе х элсмент X жиынының элементі емес) деп оқылады. Егер X жиынының барлық элементтері У жиынының да элементтері болса, онда X жиыны У жнынның жиыншасы деп аталып, былай белгіленеді:

\[O\mathbf{1},\mathbf{v}\]

нсмесе

\[\mathbf{U}\supset O\]

жәнс X жиыны Ү жиынының жиыншасы немесе X жиыны Ү жиынына тиісті деп оқылады.

Анықтама. х, у, z, . . . элементтерінен анықталған R жиыны сызықты кеңістік деп атау үшін мына төмендегі үш ереже орындалуы керек:

I. кез келген

\[\sigma\in R\]

пен

\[\phi\in R\]

элементтері үшін осы элементтердің қосындысы деп аталатын х + у үшінші элемент анықталып және ол R жиынынын элементі болса, яғни х + у

\[\in R\colon\]

II. кез келген

\[\sigma\in R\]

және а саны үшін х пен а -нің көбейтіндісі деп аталатын а • х элементі анықталып және ол R жиының элементі болса, яғни а •

\[\scriptstyle\sigma\in R\]

;

III. жоғарыдағы екі ереже мына аксиомаларі бағынса:

1) кез келген,

\[\varnothing\in R\]

, үшін

\[\scriptstyle\phi\in R\]

үшін қосындысының ауыстырымдылық ; қасиеті орындалады, яғни х+у= у + х;

2) кез келген

\[\sigma\in R\]

\[\phi\in R\]

\[z\in R\]

үшін қосындының терімділік қасиеті орындалады, яғни (х + у) +z = х +(y+z) ;

3) кез келген

\[\scriptstyle\sigma\in R\]

элемент үшін 0- нөл элемент деп аталатын элемент табылып х + 0 = х теңдігі орындалады, мұндағы 0

\[\in R\]

(кеңістіктің нол элементі мен нол санын бірдей әріппен белгілейміз, ал олар сөз болған жағдайда оларды мағынасына қарап бір-бірінен ажырататын боламыз) ;

4) кез келген

\[\varnothing\in R\]

үшін осы элементтің кері элементі деп аталатын

х элементі бар және х + (-х) - 0 болады;

5) кез келген

\[\varnothing\in R\]

үшін 1 • х = х;

6) кез келген

\[\sigma\in R\]

және

\[a\ \beta\]

сандары үшін

\[a\left(b\,\ \bar{\sigma}\right)=\left(a\,\cdot\beta\,\right)x\]

теңдігі орындалады;

7) кез келген

\[\scriptstyle\sigma\in R\]

және

\[a\ \iint\]

сандары үшін

\[(a\ +b\mathbf{\alpha})x=a\ x+\beta y\]

тсндігі орындалады;

8) кез келген

\[\sigma\in R\]

\[\scriptstyle\phi\in R\]

және а саны үшін а (х + у) = а х + а у теңдігі орындалады.

Анықтамадағы сандар нақты сандар болып ондағы үшін ереже орындалса, онда R сызықты нақты кеңістік , ал олар комплекс сандар болса, онда R - сызықты комплекс кеңістік деп аталады.

Сызықты кеңістіктің элементтері вектор деп аталады. Сондықтан, алдағы тарауларда сызықты кеңістіктің элементтңрін вектор деп айтатын боламыз, бірақ вектордың сызықша белгісін (х) қоймай басқа жазылу таңбасын сақтаймыз, мысалы, х = { х ₁ , х ₂ , х ₃ }. Сызықты нақты кеңістікті қарастырайық. Оның мынадай қасиеттері бар.

1. Сызықты кеңістіктің нөл элементі тек біреу ғана.

Дәлелдеу үшін кері жориық, яғни сызықты кеңістіктің нөл элементі екеу делік мәні: олар 0 ₁ мсн 0 ₂ болсын. Онда, кез келген

\[\sigma\in R\]

үшін х + 0 ₁ = х : және х + 0 ₂ = х ^- теңдіктері орындалады. Осыдан 0 ₂ + 0 ₁ = 0 ₂ және 0, + 0 ₂ =0 ₁ мұндағы 0 ₂ + 0 ₁ = 0 ₁ + 0 ₂ . Олай болса, 0 ₁ = 0 ₂ .

2. Сызықты кеңістіктің х элементінің кері элементі тек біреу ғана.

Дәлелдеу үшін кері жориық, яғни х -элементінің кері элементі екеу және олар у пен z болсын, яғни х + у = 0 және х + z=0. Енді сызықты кеңістігінің III ережесін пайдаланайық

y + x + z = y + (x+z) = y + 0 = y,

y + x + z = (y+x) + z = 0 + z = z.

Олай болса, у = z.

3. Сызықты кеңістіктің кез келген х элементі үшін 0 • х = 0 теңдігі орындалады.

Кез келген

\[\textstyle\beta\]

санын алайық. Сонда 0 ٠ х =

\[(b-\beta\,)\]

х=

\[b\ x-\partial\ x=b\ x+(c\ \beta\ x)=0\]

4. Кез келген а саны мен 0

\[\in R\]

үшін а • 0 = 0 теңдігі орындалады.

а • 0 = а • (0 + 0) = а • 0 + а • 0. Осы теңдіктің екі жағына - а • 0-ді қосайық: а • 0 + а • 0 = = а • 0 + а • 0 - а • 0. Осыдан 0 = а • 0.

5. Егер а • х - 0 болса, онда не х = 0, нс а = 0, мұндағы,

\[\varnothing\in R\]

, а -кез келген сан.

Алдымен

\[a\ \neq0\]

деп ұйғарып, х = 0 болатынын дәлелдейік. Шынында да,

\[x=1\times\!\Omega=_{\frac{\zeta}{\Theta}}^{\frac{\zeta}{2}}a\ {\frac{\ddot{\vartheta}}{\vartheta}}x\!=\!{\frac{1}{a}}\left(\alpha\ \times\!x\right)={\frac{1}{a}}\times\!0=0.\]

Енді

\[x\div\not\leftrightarrow0\]

деп ұйғарып,

\[{\mathcal{Q}}\]

= 0 болатынын оқырмандарға жаттығу ретінде ұсынамыз.

6. (-1) • х элемент х элементінің кері элементі, мұндағы

\[\varnothing\in R\]

Шынында да, х + (-1) х = 1 • х + (-1) [1 +(-1) ], ٠ х = 0 ٠ х =0.

Сондықтан (-1) х = - х .

Сызықты кеңістікке мысалдар:

1 - м ы с а л . Дәрежесі п -нен кіші әрі п -ге тең көпмүшеліктер жиынын қарастырайык. Бұл жиында көпмүшеліктерді қосу мен санды көлмүшелікке көбейту амалдары орындалатынына оңай көз жеткізуге болады. Сондықтан дәрежесі п -ненкіші әрі п -ге тең көпмүшеліктер жиыны сызықты кеңістік құрайды.

Кез келген дәрежелі көпмүшеліктегі; . жиыны да сызықты кеңістік түзейді.

2-м ы с а л. Бірдей дәрежелі көпмүшеліктер жиынын қарастырайық, мысалы дәрежесі п > 0 болсын. Бұл жиын сызықты кеңістік түземейді. Себебі, санды көпмүшелікке көбейту амалы орындалғанмен де, көпмүшелікті көпмүшелікке қосып, қосындының дәрежесі п -нен кіші көпмүшелік аламыз.

3-м ы с а л . [а, b] сегментте анықталған әрі үзіліссіз функциялар жиынын қарастырайық. Мұндай функциялардың жиыны математикалық талдауда С [а; b ] - символымен белгіленеді,

\[f(x){\hat{\mathbb{I}}}\ C[a,b]\,x\in[a;b].\]

Үзіліссіз функцияларды қосу және нақты санды үзіліссіз функцияға көбейту амалдары орындалғанда [а; b] сегментте анықталған үзіліссіз функцияларды аламыз. Сондықтан, С[а ; b] кеңістігі сызықты кеңістік түзейді.

Сызықты кеңістіктің базисі мен өлшемі.

Анықтама. Егер R сызықты кеңістігінде 1)

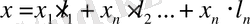
\[\begin{array}{c}{\int_{{\bf l}}{\bf l}_{\bf l}\,\rangle\,\ne\approx\,\cdot\,\approx\,\rangle\,\not=\,\frac{1}{\bf r}\,\mathrm{~}\nonumber}\end{array}\]

элементтері сызықты тәуелсіз болса, 2) сызықты кеңістіктің әр х элементі үшін х ₁ , х ₂ . . . , х _n нақты сандар табылып

теңдігі орындалса,

\[\begin{array}{c}{\int_{{\bf l}}{\bf l}_{\bf l}\,\rangle\,\ne\approx\,\cdot\,\cdot\,\rangle\,\not=\,\frac{1}{n}\,\mathrm{~}}\end{array}\]

онда элементтерінің жиынтығы осы кеңістіктің базисі деп аталады. Бұл жағдайда (2. 5) теңдігі л элементінің

\[\tilde{I}_{1},\tilde{J}_{2},\cdot\cdot\cdot\cdot\cdot\cdot\tilde{I}_{n}\]

базисі арқылы жіктелінуі, ал х ₁ , х ₂ . . . , х _n - нақты сандар х элементінің координаттары деп аталады және х = [х ₁ , х ₂ , . . . , х _л } символымен белгіленеді.

Анықтама. R сызықты кеңістігі п- өлшемді кеңістік деп аталады, егер осы кеңістікте п сызықты тәуелсіз элементтср бар болып, ал кез келген п + 1 элементтері сызықты тәуелді болса және ол R _п - әрпімен, белгіленеді. Бұл жағдайда п -саны R _п сызықты кеңістігінің өлшемі деп аталады да

\[\dim R_{n}=n\]

символымен белгіленеді.

Мысалы, дәрежесі п - 1-ден кіші және п - 1-ге тең көпмүшеліктердің жиынтығы п -өлшемді кеңістік. Себебі бұл кеңістікте п дәрежелі көпмүшелік, яғни

\[\textstyle\bigsqcup_{j}f_{,}f^{2}{}_{,\cdot\cdot,j}^{n-1}\]

сызықты тәуелсіз. Жазықтықтағы векторлар жиынының өлшемі 2-ге, кеңістіктегі векторлар жиынының өлшемі 3-ке, ал R _п - п өлшемді кеңістігінің өлшемі п- ге тең.

Егер R сызықты кеңістігінде шексіз сызықты тәуелсіз элементтер бар болса, онда ол кеңістік шексіз кеңістік деп аталады. Мысалы, С[а; b] -кеңістігі шексіз кеңістік.

Себебі бұл кеңістікте шексіз сызықты тәуелсіз функциялар бар.

Егер кеңістіктің өлшемі шектелген болса, онда ол кеңістік шектелгеп сызықты кеңістік деп аталады.

Негізіндс біз бұл тарауда п өлшемді кеңістіктерді қарастырмақпыз.

Теорема. R _п - сызықты кеңістігінің х элементі

\[\begin{array}{c}{\int_{{\bf l}}{\bf l}_{\bf l}\,\rangle\,\ne\ast_{\bf\varphi}\,\ldots\,\rangle\,\not=\,\frac{1}{n}}\end{array}\]

базисі арқылы жіктелінуі

\[{\mathcal{X}}={\mathcal{X}}_{1}{\mathcal{Y}}_{1}+{\mathcal{X}}_{2}\left.{\mathcal{Y}}_{2}\right.\cdot\cdot\cdot+{\mathcal{X}}_{n}\cdot{\mathcal{I}}_{n}\]

тек біреу ғана.

Дәлелдеуі. Теореманы дәлелдеу үшін кері жориық, яғни R _п кеңістігінің х элементі 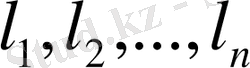базисі арқылы жіктелуінсн өзгеше жіктелсін, яғни

\[{\mathcal{X}}={\mathcal{X}}_{1}\ \S_{l}+{\mathcal{X}}_{2}^{1}{\mathcal{A}}_{2}\ldots+{\mathcal{X}}_{n}^{1}\cdot l_{n}\]

(6) мсн (5) жіктелулерінің айырымын қарастырайық:

\[0=\left(x_{1}^{\prime}\ {\mathcal{D}}_{1}\right)d_{1}+\left(x_{2}^{\prime}\mathcal{D}_{2}\right)\!\mathcal{A}_{2}+...+\left(x_{n}^{\prime}\mathcal{D}_{n}\,\right)\!\cdot\!l_{n}\]

(7) теңдіктен және

\[\begin{array}{c}{\int_{{\bf l}}{\bf\cdot}\int_{{\bf2}}{\bf\cdot}\cdot{\bf\cdot}\cdot{\bf\cdot}\cdot{\frac{}{\cal l}}_{n}}\end{array}\]

- базисінің сызықты тәуелсіздігінен