Еселі интеграл ұғымы

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 45 бет
Таңдаулыға:

КІРІСПЕ

Математика ғылымы барлық ғылымдардың арасында ерекше орын алады. Математика нақты әлемнің кеңістіктегі формалары мен сандық қатынастары туралы ілім. Бұл арада кеңістіктегі формалар мен сандық қатынастар ұғымдары нағыз кең және жалпы түсінуді қажет етеді.

Математика өзінен басқа ілімдер үшін сан және белгі (символ) түрінде табиғаттың әртүрлі құбылыстарының ара қатынастарын өрнектейтін тіл болып саналады. Міне осы тұрғыдан да «ғылым өзінің шыңына Математиканы пайдаланғанда ғана жететін болады».

Ал бұл жағдай нақты объектілердің (заттардың) мәндерін толық түрде кескіндейтін математикалық модель құру арқылы іске асатын болады. Бірақ Математикалық модельдеуді іске асыруды игеруден бұрын және өзінің іс-әрекетінде Математиканы қолданудан бұрын инженер-технолог, химик, физик, экономист немесе биолог т. б. мамандық иелері алдымен Математиканың негізін, оның тәсіл-әдістерін игеруі керек.

Қазіргі ғылым мен техникада математикалық зерттеулер, модельдер,

жобалар өте үлкен роль атқарады. Ол қазіргі ақпараттар жүйесінің дамуына

тікелей байланысты. Демек математикалық нақты сандар шешімін табуға

табысты қолдану мүмкіншілігін кеңейтеді.

Математика фундаменталды пән, одан дәріс беру төменгі жағдайды

қарастырады:

а) ойдың логикалық және алгоритмдік дамуын;

ә) негізгі зерттеу әдістерін меңгеру және математикалық есептердің

шешімдерін таба білу;

б) математикалық негізгі сандық әдістерін меңгеру және оны

компьютерде орындау;

в) математикалық білімді өз бетінше ұғып алуға еңбектену, қолданбалы

инженерлік және экономикалық есептерге талдау жүргізу.

Математиканың жалпы курсы дәстүрлі мамандар үшін оқу жоспары

бойынша арнайы және жалпы техникалық пәндерді табысты оқытуға

маңызды мәні бар инженерлер білімдерінің математикалық фундаментін

қалайды.

Зерттеудің көкейтестілігі. Болашақ математика пәнінің мұғалімдерін даярлау үшін математикалық анализдің физика, механика және т. б. салаларда қолданбалылығын пайдалану іргелі білімді меңгеруге кең көлемде мүмкіндік туғызады. Бұл диплом жұмысында еселі интегралдар үшін болған негізгі білімдер жүйесі жайында, сондай-ақ олардың шешімдерін табу әдістері және геометриялық, физикалық қолданыстары көрсетіледі.

(D) облысында анықталған z=f(x, y) екі айнымалының функциясын қарастырып, оның интегралының анықтамасын және екі айнымалының интегралынның механикалық және геометриялық мәндері қаралған.

Осы тұрғыда болашақ математика пәнінің мұғалімдерін даярлау үшін математикалық анализдің физика, экономика, топография, механика және т. б. салаларда қолданбалылығын пайдалану іргелі білімді меңгеруге кең көлемде мүмкіндік туғызады. «Математикалық анализ» курсындағы беттік интегралдар бөлімінің практикалық мазмұнды есептерді шешуде қолданылуын көрсету арқылы бұл тарауларды меңгеруде жақсы нәтижедерге жетуге болады.

Зерттеудің мақсаты: Диплом жұмысын жазудағы мақсат «Математикалық талдау» пәнінен алған теориялық білімді практикада тереңірек қолдану көзделген. Диплом жұмысын еселі интегралдар тақырыбын өткен кезде және практикалық сабақтар өткенде пайдалануға болады.

Дипломдық жұмыстың құрылымы: Бұл дипломдық жұмыс кіріспе, екі тарау, қорытынды және пайдаланған әдебиеттер тізімінен тұрады.

Бірінші бөлімде еселі интегралдар жайлы баяндалса, екінші бөлімде еселі интегралдардың кейбір механикада, физикада қолданыстарының шешу әдістері қарастырылды.

1 ЕСЕЛІ ИНТЕГРАЛДАР

1. 1 Еселі интеграл ұғымына келтірілетін есептер.

Еселі интеграл ұғымы

Декарт координат жүйесіне келтірілген қайсы бір (D ) фигурада үздіксіз түрде массасы таралған болсын. Орташа тығыздық деп, осы фигура массасының оның ауданына қатынасын айтатыны белгілі, .

Бірақ орта тығыздық фигураның кез-келген нүктесіндегі тығыздықты толық анықтамайды. Сондықтан да кез-келген нүктедегі шын тығыздықты орта тығыздықтың кішкене фигура нүктеге айналатын болғандағы шегін алады:

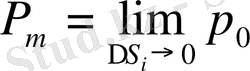
Егер фигураның әр бір тең ауданына тең масса келетін болса, онда пластина ( фигура ) біртекті деп аталады. Мұндай пластинаның тығыздығы әрбір нүктеде бірдей болады да, ол орта тығыздыққа тең болады. Егер пластина біртекті болмаса, онда оның тығыздығы нүктеден нүктеге өзгеріп отырады, яғни нүкте координатасы орнының ( екі айнымалының ) функциясы болып табылады, яғни .

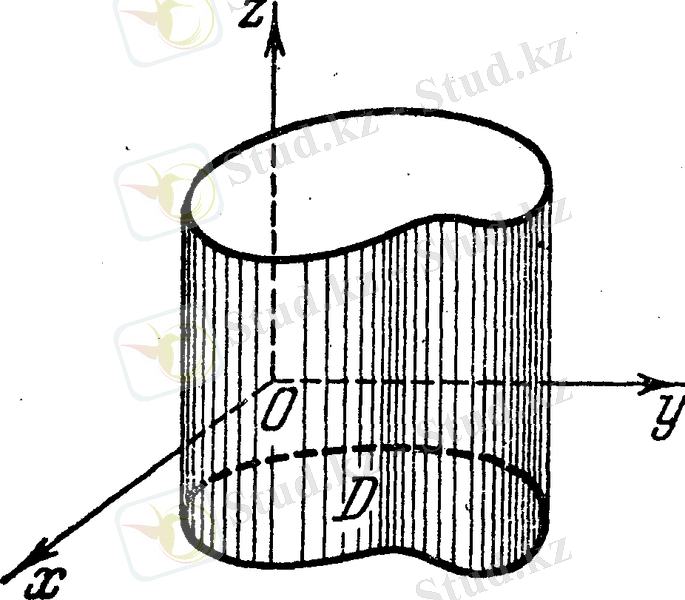
Сурет1

Сонымен берілген ( D ) фигурасы, осы фигурада анықталған және үздіксіз функциясы арқылы оның массасын табу керек болсын.

Ол үшін (D ) фигурасын кез-келген тормен n бөлікке бөлеміз:

.

Олардың диаметрлерін және аудандарын және арқылы белгілейміз. ( -кішкене фигураның ең қашықтықтағы екі нүктесінің ара қашықтығы D нолге ұмтылғанда функциясы көп өзгеріп үлгермейді. Олай болса оны тұрақты деп қабылдауға болады. Ендеше, (D ) вигураның торкөзінің массасы

,

ал (D) фигураның массасы жуық қосындысына тең болады. Оның дәлдігі -ның аздығына тәуелді. Сондықтан

.

Бұл алынған қосынды функциясы үшін интегралдық қосынды болып саналады. өйткені функциясы (D ) фигурасында үздіксіз функция.

Міне осы сияқты есепдарды ғылымның және техниканың кез-келген саласынан көптеп келтіруге болады. [1]

Ал енді осы сияқты есептердің мәніне тоқталмай-ақ ( D ) облысында анықталған екі айнымалының функциясын қарастырып, оның интегралының анықтамасын және екі айнымалының интегралының механикалық және геометриялық мәндеріне тоқталайық. [2]

1. 2 Екі еселі интегралдың анықтамасы

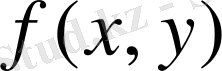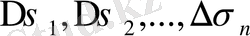ХОУ жазықтығында квадратталатын тұйық облыста функциясы берілген. облысын облыстарының ортақ ішкі нүктелері болмайтындай кез келген 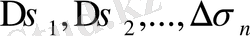n бөліктерге бөлейік. Әрбір 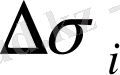тұйық облысында (ішінде немесе шекарасында) кез келген 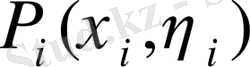нүктесін таңдаймыз да осы нүктедегі 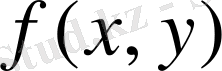функциясының мәнін 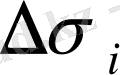ауданына көбейтеміз. Осындай барлық көбейткіштерді қосып, келесі қосындыны аламыз:

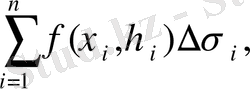(1. 2)

бұл 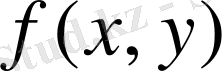функциясының облысындағы интегралдық қосындысы деп аталады. Интегралдық қосынды облысын 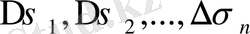бөліктерге бөлуден және осы бөліктерде нүктелерін таңдап алудан тәуелді, яғни облысындағы 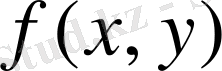функциясы үшін шексіз көп интегралдық қосындылардың жиынын құруға болады.

Шектік операцияға көшпес бұрын облыс диаметрі және облысты бөлу қадамы ұғымдарын енгізейік. Тұйық облыстың (екі немесе үш өлшемді кеңістіктегі) диаметрі деп осы облыстың шекарасындағы екі нүктенің ең үлкен арақашықтығын айтамыз. Облысты ақырлы бөліктерге бөлу қадамы деп бөлік облыстардың диаметрлерінің ең үлкенін айтамыз.

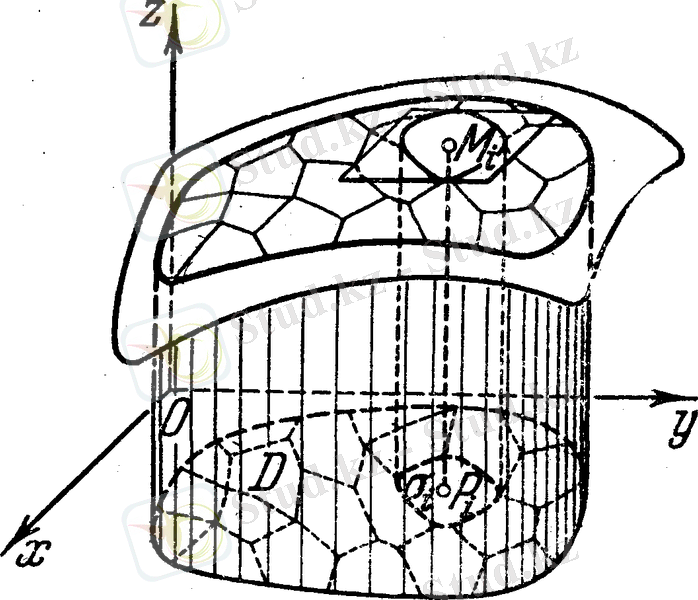
Cурет 2

арқылы облысын 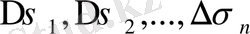бөліктерге бөлу қадамын белгілейміз. Облысты шексіз ұсақ бөліктерге бөлу және оған сәйкес облысты бөлу n санының шексіз артуынан тұратын процесті « облысын бөлу қадамы нөлге ұмтылады» деп сипаттауға болады.

Егер облысының 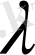бөлу қадамы нөлге ұмтылғанда (1. 1) интегралдық қосындының шегі бар болса, онда бұл шекті 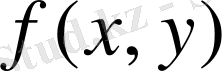функциясының облысы бойынша екі еселі интегралы деп атайды және

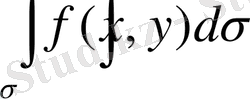немесе .

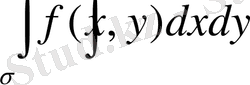символдарымен белгілейді. Мұндағы 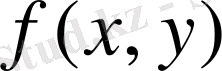- интеграл астындағы функция, - интегралдау облысы, x және y - интегралдау айнымалылары, 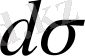(dxdy) - аудан элементі. Осыдан, анықтама бойынша

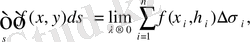
егер бұл шек бар болса.

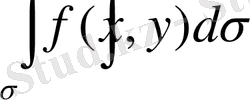екі еселі интегралы бар 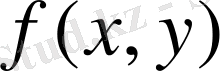функциясы облысында интегралданады деп аталады.

1. 3 Екі еселі интегралдың бар болуы және

қасиеттері

Шынында да, барлық функциялар үшін облысы бойынша екі еселі интеграл табылады ма, егер жоқ болса, қандай функциялар үшін екі еселі интегралдар анықталады деген сұрақ туындайды.

облысында интегралданатын функция тұйық облысында шектелген болуы керек, өйткені кері жағдайда нүктелерін таңдауда интегралдық қосындыны абсолют шамасы бойынша өте үлкен етіп алуға болады, яғни 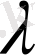нөлге ұмтылғанда интегралдық қосындының шегі болмас еді.

Екі еселі интегралдың бар болуының жеткілікті шарттарын қарастырайық.

Теорема 1. Егер 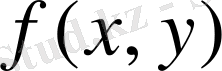функциясы тұйық облысында үзіліссіз болса, онда 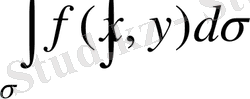екі еселі интеграл бар болады.

Бұл теореманың дәлелдеуін анықталған интегралдың сәйкес теоремасына сай дәлелдеуге болады.

Теорема 2. Егер 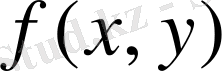функциясы тұйық облыста шектелген және үзіліссіз болса, онда 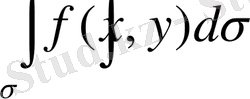екі еселі интеграл бар болады. Төмендегі функциялар (1 немесе 2) теореманың шарттарын қанағаттандырады деп ұйғарып, екі еселі интегралдың негізгі қасиеттерін келтірейік. Бұл қасиеттердің дәлелдеуін анықталған интегралдың қасиеттеріне сай дәлелдеуге болады.

1. 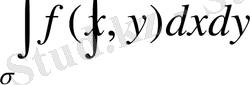екі еселі интегралы интегралдау айнымалысын белгілеуден тәуелді емес.

2. k тұрақты көбейткішті екі еселі интеграл таңбасы алдына шығаруға болады:

3. Екі функцияның қосындысының екі еселі интегралы осы функциялардың екі еселі интегралдарының қосындысына тең:

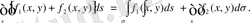
4. Егер облысы және облыстарына бөлінсе, онда

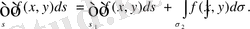
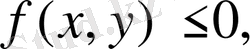5. Егер барлық облысында онда

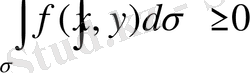
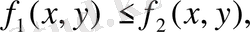6. Егер барлық облысында онда

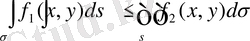
7. Егер 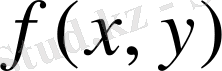функциясы облысында берілсе, онда

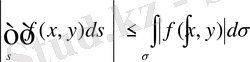
1. 4 Екі еселі интегралдың геометриялық мағынасы

Цилиндрлік дененің көлемін табу есебіне оралайық. Қарастырып отырған 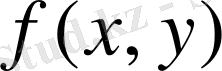функциясы тұйық облысында үзіліссіз болса, онда 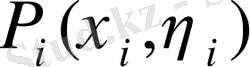нүктелері 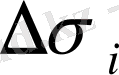тұйық облыстарында қандай болса да

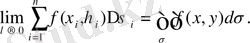
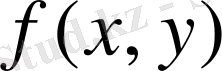функциясы 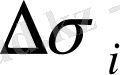облыстарында (m _i ) ең кіші немесе (M _i ) ең үлкен мәндерін қабылдайтындай етіп, 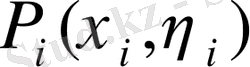нүктелерін таңдай отырып, келесі теңдікті аламы:

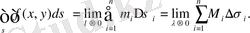
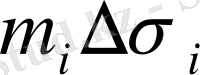және 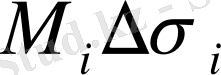қосылғыштары табаны 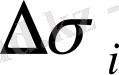болатын цилиндр көлеміне тең. 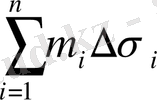және 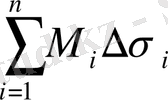қосындылары сәйкесінше іштей және сырттай сызылған V цилиндрлік денелердің көлемдеріне тең. 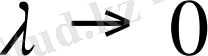бұл көлемдер ортақ шекке ие болады, берілген дене кубталады және оның V көлемі екі еселі интегралға тең:

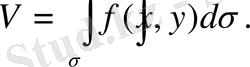
Осыдан екі еселі интегралдың геометриялық мағынасы: тұйық облысында теріс емес, үзіліссіз 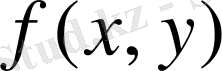функциясының 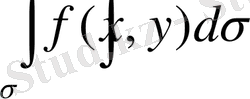екі еселі интегралы жоғарыдан 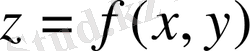бетпен шектелген, XOY жазықтығындағы табаны болатын цилиндрлік дененің көлеміне тең. Егер облысында 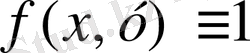болса, онда цилиндрлік дене табаны ал биіктігі болатын цилиндрді білдіреді. Оның көлемі сан жағынан табанының ауданына тең. Осылайша, екі еселі интеграл арқылы облысының ауданын бұрыннан белгілі формуламен есептейміз 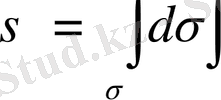немесе .

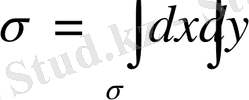1. 5 ЕКІ ЕСЕЛІ ИНТЕГРАЛДЫҢ КЕЙБІР ГЕОМЕТРИЯЛЫҚ

ЖӘНЕ МЕХАНИКАЛЫҚ ҚОЛДАНУЛАРЫ

Екі еселі интегралды жоғарыда айтылғандай жазық фигураның ауданын, дененің көлемін есептеуге қолдануға болады. Бірнеше мысалдар қарастырайық.

1-мысал: y ² =x+1, x+y=1 сызықтармен шектелген $\sigma$ $\sigma$ облысының ауданын тап. $\sigma$ $\sigma$ облысы сол жағынан x=y ² -1 парабола доғасымен және оң жағынан x=1-y түзуімен шектелген, параболалық сегмент болып табылады.

Параболаның теңдеуімен түзу теңдеуін бірге шеш отырып, олардың қиылысу нүктелерінің ординатасын табамыз: y=-2, y=1

Осыдан

$\sigma = \iint_{a}^{}{{dx}{dy}} = \int_{- 1}^{1}{{dy}\int_{y^{2} - 1}^{y - 1}{dx}} = \int_{- 2}^{1}{\left( 2 - y - y^{2} \right) {dy} = \frac{9}{2}}\$ $\sigma = \iint_{a}^{}{{dx}{dy}} = \int_{- 1}^{1}{{dy}\int_{y^{2} - 1}^{y - 1}{dx}} = \int_{- 2}^{1}{\left( 2 - y - y^{2} \right) {dy} = \frac{9}{2}}\$

Ескерту. Егер біз интегралдау ретінде керісінше алатын болсақ $\sigma\$ $\sigma\$ облысын алдын-ала екі облысқа бөлуге болады.

2-мысал: у=x ² , y=1, z=0, z=x ² +y ² , беттерімен шектелген V дененің көлемін тап.

Берілген дене табаны $\sigma$ $\sigma$ болатын, жоғарыдан $z = x^{2} + y^{2}$ $z = x^{2} + y^{2}$ параболойдпен шектелген цилиндрлік дене болғандықтан:

$V = \iint_{}^{}{\left( x^{2} + y^{2} \right) {dx}{dy} =}2\int_{0}^{1}{dy}\int_{0}^{\sqrt{2}}{(x^{2} + y^{2}) {dx}} = 2\int_{0}^{1}{(\frac{1}{3}y^{\frac{3}{2}} + y^{\frac{5}{2}}) {dx}} = \frac{88}{105}$ $V = \iint_{}^{}{\left( x^{2} + y^{2} \right) {dx}{dy} =}2\int_{0}^{1}{dy}\int_{0}^{\sqrt{2}}{(x^{2} + y^{2}) {dx}} = 2\int_{0}^{1}{(\frac{1}{3}y^{\frac{3}{2}} + y^{\frac{5}{2}}) {dx}} = \frac{88}{105}$

3-мысал: Жақтары $x = \pm 1, \ y = \pm 1$ $x = \pm 1, \ y = \pm 1$ және $x^{2} + y^{2} = 4 - z$ $x^{2} + y^{2} = 4 - z$ , $x^{2} + y^{2} = 4(z + 2)$ $x^{2} + y^{2} = 4(z + 2)$ параболойдтармен шектелген призмалық дененің көлемін тап.

Дененің V көлемін XOY жазықтығына сәйкес жоғарғы жақтарында жатқан екі дененің көлемдерінің V ₁ және V ₂ қосындысы түрінде қарастырамыз.

Яғни

${\ \ \ \ \ \ \ \ \ \ \ \ \ V}_{1} = \iint_{}^{}{(4 - x^{2} - y^{2}) }dxdy = 4\int_{0}^{1}{dx}\int_{0}^{1}{(4 - x^{2} - y^{2}) }dy = \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 4\int_{0}^{3}{\left( 4 - x^{2} - \frac{1}{3} \right) {dx} = \frac{40}{3}}$ ${\ \ \ \ \ \ \ \ \ \ \ \ \ V}_{1} = \iint_{}^{}{(4 - x^{2} - y^{2}) }dxdy = 4\int_{0}^{1}{dx}\int_{0}^{1}{(4 - x^{2} - y^{2}) }dy = \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 4\int_{0}^{3}{\left( 4 - x^{2} - \frac{1}{3} \right) {dx} = \frac{40}{3}}$

$V_{2} = - \iint_{}^{}{(\frac{x^{2} + y^{2}}{4}} - 2) dxdy = - 4\int_{0}^{1}{(\frac{x^{2} + y^{2}}{4}} - 2) dy = \frac{22}{3}$ $V_{2} = - \iint_{}^{}{(\frac{x^{2} + y^{2}}{4}} - 2) dxdy = - 4\int_{0}^{1}{(\frac{x^{2} + y^{2}}{4}} - 2) dy = \frac{22}{3}$

$V = V_{1} + V_{2} = \frac{62}{3}$ $V = V_{1} + V_{2} = \frac{62}{3}$

S бетінің ауданын табу формуласы

$S = \iint_{}^{}{\sqrt{1 + f_{x}^{'\ 2}(x, y) + f_{y}^{'\ 2}(x, y) }{dx}{dy}}$

1. 6 Дұрыс облыс және қайталамалы интеграл

ұғымы

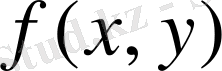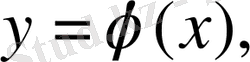
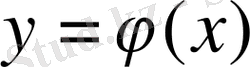
Теорема 1. Егер функциясы x=a, y=b (a<b), 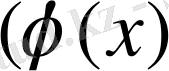и 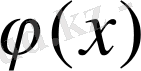- [a, b] кесіндісінде үзіліссіз функциялар, және осы кесіндіде 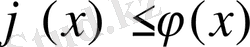) сызықтарымен шектелген тұйық облысында үзіліссіз болса, онда

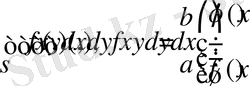(1. 3)

екі еселі интегралды есептеуге мүмкіндік беретін теңдік орындалады.

(1. 3) теңдігінің оң жағындағы қайталанбалы интегралы келесі түрде жазылады:

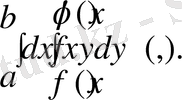
Теорема 2. Егер 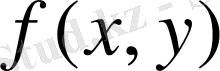функциясы y=c, y=d (c<d), 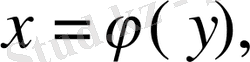Equation. 3 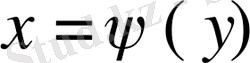Equation. 3 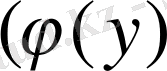Equation. 3 және 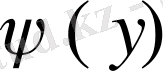- [c, d] кесіндісінде үзіліссіз және 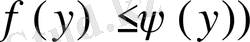сызықтармен шектелген тұйық облысында үзіліссіз болса, онда

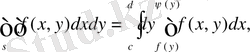(1. 4)

екі еселі интегралды есептеуге мүмкіндік беретін теңдік орындалады.

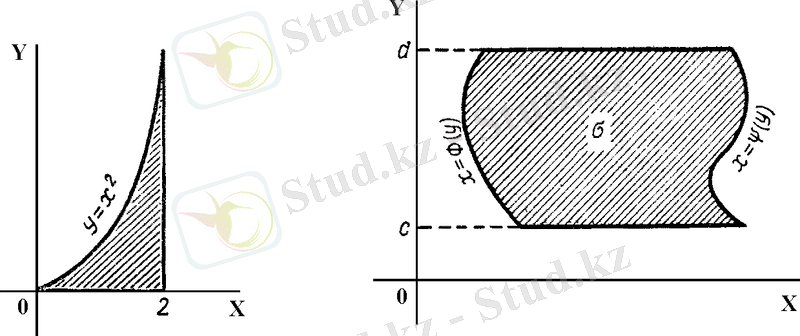
Cурет 3

Екі еселі интегралды қайталанбалы интеграл арқылы (1. 4) формуласы бойынша бірінші ішкі интеграл 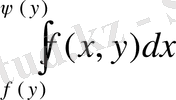Equation. 3 есептеледі, мұнда у тұрақты, өзгеру шектері у-тен тәуелді ( Equation. 3 облысы үшін) . Содан кейін у-тен тәуелді функция 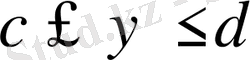аралығында у бойынша интегралданады. [5]

4-мысал: 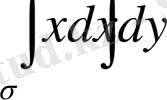интегралын 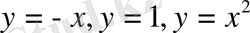сызықтарымен шектелген облысы бойынша есепте.

2-ші теореманың шарттары орындалып тұрғандықтан, (1. 4) формуласын қолданамыз:

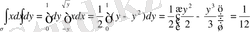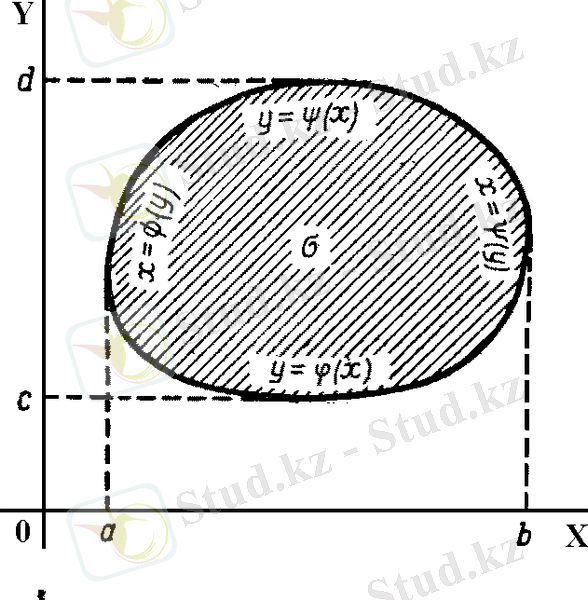
Cурет 4

Егер 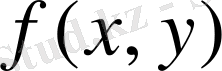Equation. 3 функциясы Equation. 3 тұйық облысында үзіліссіз, 1 және 2 теореманың шарттарын бір уақытта қанағаттандырса, онда 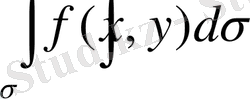Equation. 3 екі еселі интегралын есептеуде интегралдау ретінің кез келгенін алуға болады (сыртқы интеграл x бойынша, ішкі интеграл y бойынша немесе керісінше) . Есепы, егер облыс шекарасының ОХ осіне параллель әрбір түзуі және Оу осіне параллель әрбір түзуі тек екі нүктеде қиылысса, онда (1. 3) және (1. 4) формулаларын да қолдануға болады, яғни

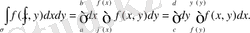
Егер облысы - x=a, x=b, y=c және y=d түзулерімен шектелген тік төртбұрыш, ал f(x, y) - 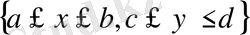тік төртбұрышында үзіліссіз болса, онда (1. 3) және (1. 4) формулаларын қолданып,

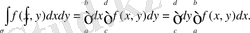
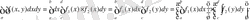
аламыз.

Есепы, егер - 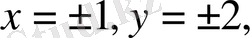тік төртбұрыш болса, онда

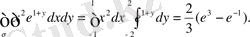
5-мысал Интегралдау ретін өзгертіңіз.

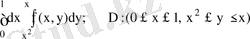
Шешуі: D аймағы 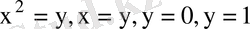, осыдан

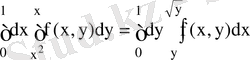6-мысал: Интегралдау ретін өзгертіңіз.

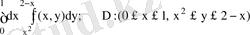
Шешуі: D=D ₁ +D ₂ болғандықтан (сурет 5),

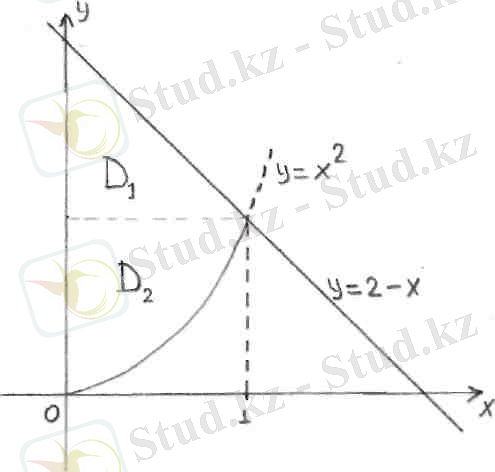
Cурет 5

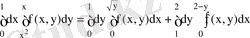
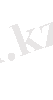
7- мысал: D облысы 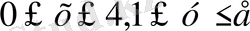тікбұрышы болғанда 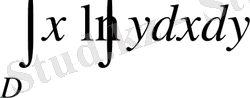екі еселі интегралды есептеңіз.

Шешуі:

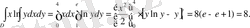
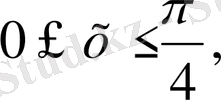
8-мысал: D облысы 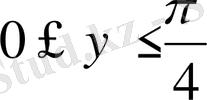квадраты болғанда 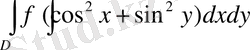екі еселі интегралды есептеңіз.

Шешуі:

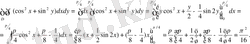
9- мысал: Интегралдау ретін өзгертіңіз

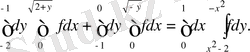
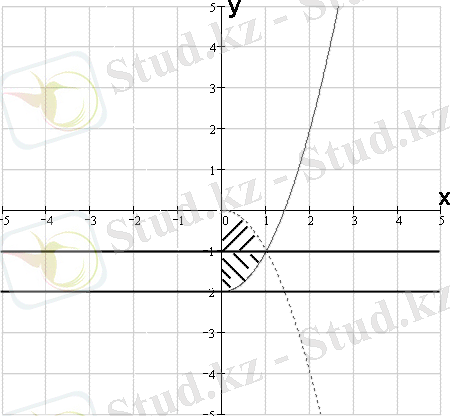
Cурет 6

10- мысал: Есептеңіз

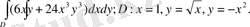
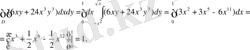
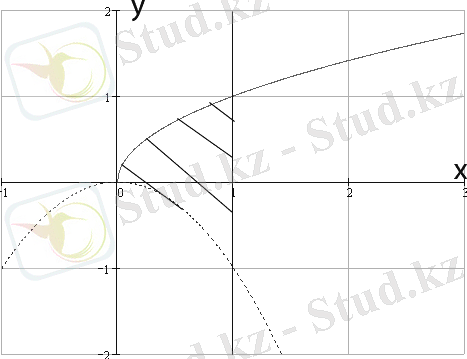
Сурет 7

11- мысал:

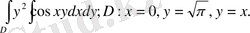
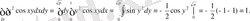
Сурет 8

12- мысал: Есептеңіз 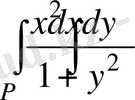, мұнда Р тіктөртбұрыш [0, 1; 0, 1] .

. ∆

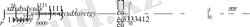13- мысал: Р : y = x ³ , y + x =2, x =0 шектелген. 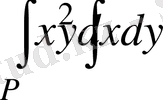есептеңіз.

Анүктесінің координатасын табамыз:x3=2-x, x3+x-2=0, x=1.

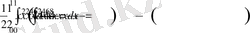
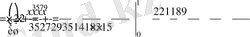
Сурет 9

14- мысал: Р : y ² =3 x +9, y =3- x шектелген . 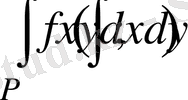интегралын қайталама

интегралдың екі әдісімен есептеңіз.

∆ Функция графигңнен қиылысу нүктелерін

табамыз:

(3 -x ) ² =3 x +9, 9-6 x + x ² -3 x -9=0,

x ² -9 x =0, x ( x -9) =0, x =0, x =9,

y =3, y =-6.

3 x +9= y ² -9, 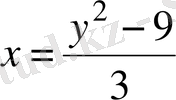. Бірінші теңдеуден өрнектейміз.

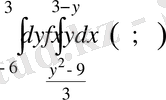1. 7 Екі еселі интегралда айнымалыларды

ауыстыру

Якобиан және оның геометриялық мағынасы. UOV және XOY декарттық жүйе координатасында екі жазықтық берілсін. Сәйкесінше UOV және XOY жазықтықтарында жатқан екі 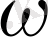және облыстарын қарастырайық, және

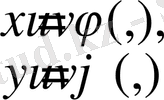(1. 5)

функциялары осы облыстағы нүктелер арасында өзара бірмәнді сәйкестікті орнатады. Яғни 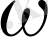облысындағы әрбір (u ₀ , v ₀ ) нүктеге облысындағы тек бір (x ₀ , y ₀ ) нүкте сәйкес қойылады, мұндағы . 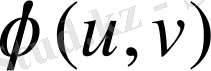және 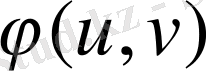функциялары облысында бірінші ретті дербес туындыларымен қоса үзіліссіз болсын. Онда

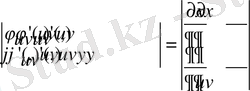
анықтауышы 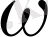облысында анықталған u және v айнымалыларынан тәуелді үзіліссіз функция болады. Бұл функционалдық анықтауыш Якоби анықтауышы немесе (1) бейнелеуінің якобианы деп аталады да 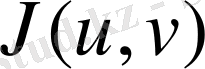немесе 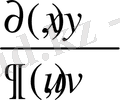символымен белгіленеді. [2]

Екі еселі интегралда айнымалыны ауыстыру формуласы

тұйық облысында үзіліссіз 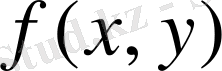функциясының

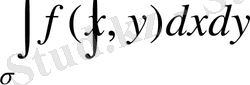Equation. 3 (1. 6)

екі еселі интегралын қарастырайық.

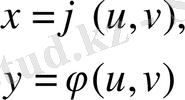(1. 7)

формулалары UOV жазықтығындағы тұйық облысын XOY жазықтығындағы тұйық облысына өзара бірмәнді бейнелейді деп ұйғарайық, және бұл бейнелеу жоғарыда айтылған барлық шарттарды қанағаттандырады.

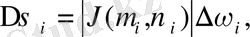
(1. 6) x және y айнымалыларынан тәуелді ( облысы бойынша) екі еселі интеграл u және v айнымалыларынан тәуелді ( облысы бойынша) екі еселі интегралына тең екендігін көрсетейік. Бұл үшін облысын жазық қисықтар көмегімен 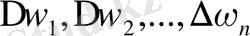n облыстарға бөлейік. Олар облысын n облыстарға 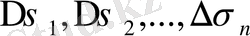бөледі. 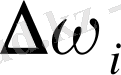және 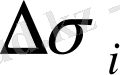сәйкес облыстардың аудандары облысындағы 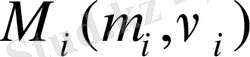нүктесімен және 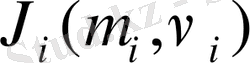якобиан бейнелеуімен байланысты. (сурет 9) . 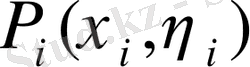арқылы 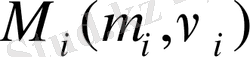нүктесінің бейнелеуі 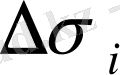облысында жатқан нүктені белгілейміз:

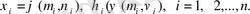
облысын 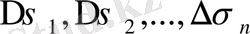облыстарға бөлу және осы облыстардан 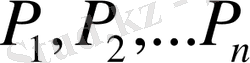нүктелерін таңдау үшін екі еселі интегралдың интегралдық қосындысын құрамыз:

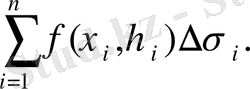
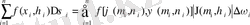(1. 8)

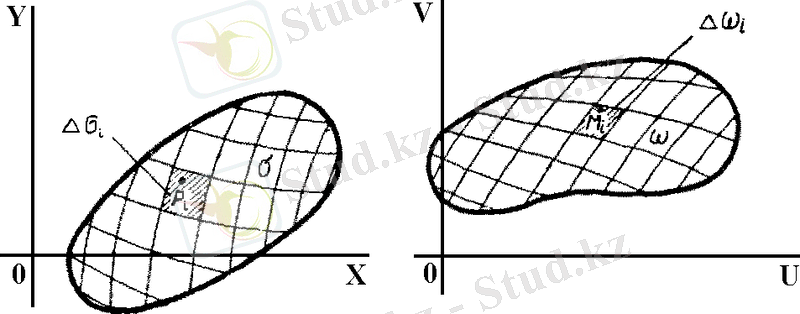
Cурет 10

Бұл теңдіктің оң жағы 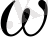Equation. 3 облысы бойынша екі еселі интеграл үшін 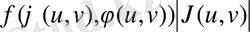Equation. 3 үзіліссіз функциядан тәуелді интегралдық қосынды тұр.

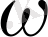облысы бойынша бөлу қадамы нөлге ұмтылғанда облысы бойынша бөлу қадамы да нөлге ұмтылады. (1. 6. 3) теңдігінде шекке көшіп:

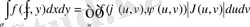
теңдігін аламыз. Бұл формула екі еселі интегралда айнымалыны ауыстыру формуласы деп аталады.

15-мысал: 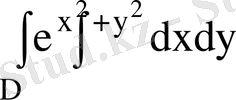, D - бірінші квадрантта жататын 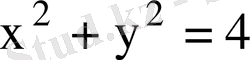дөңгелегінің бөлігі 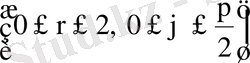. Осы интегралды есептеу керек. Шешуі: формулаларынан

; .

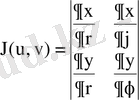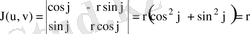Сондықтан, .

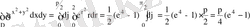16-мысал: 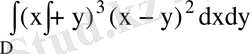интегралын есепте, егер D: 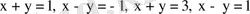түзулерімен шенелген аймақ болса. Шешуі: Айталық, 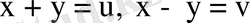болсын, онда 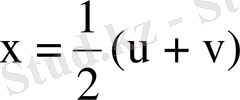, 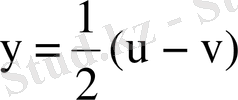. Ал түрлендіру Якобианы

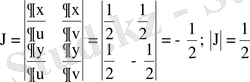Сондықтан,

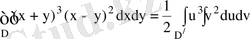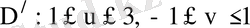
Сурет 11

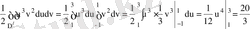17- мысал : 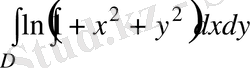есепте, мұнда D - x ² + y ² = R ² І ширекте жататын дөңгелектің жартысы.

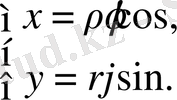
∆ Полярлық координатаға өтеміз 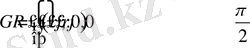облысы. Шындығында,

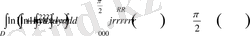
18- мысал: y = ax ² , y=bx ² параболасы (0< a < b ) мен xy=p , xy=q (0< p < q ) гиперболасымен шектелген Р фигурасының ауданын табу керек.

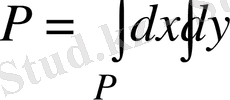∆ фигура ауданы, бірақ бұл интегаралды тікелей интегралдау қиындық тудырады. Сондықтан айнымалыларға алмастыру енгіземіз.

y = ux ² парабола ( немесе 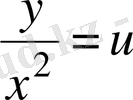) және xy=v гипербола қисықтарын қарастырайық. Р қисық сызықты фигураның нүклерінің координаттары:

(*)

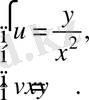Р облысы uOv жазықтығындағы тіктөртбұрышқа өтеді Q : a ≤ u ≤ b , p ≤ v ≤ q

, ,

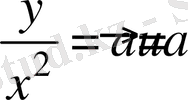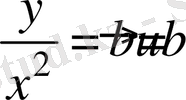, . (*) теңдеуден x және y өрнектеп және

якобианды табамыз.

⇔ ⇔ ⇔

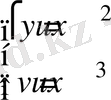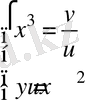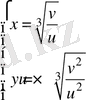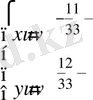
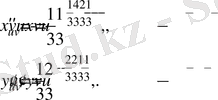
Сонда . ∆

19-мысал

интегралын (D) тік төртбұрыш облысында есептеу керек болсын тік төрт бұрыш облысында есептеу керек болсын.

Шешуі: (D) -тік төртбұрыш

немесе

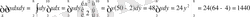
20-мысал: функциясының екі еселі интегралын ( D) үшбұрышы бойынша, яғни өстерімен және түзуімен шектелген үшбұрыш бойынша есептеу керек болсын.

Шешуі: Берілген үшбұрышты құрамыз.

Сурет 12

21 -мысал: екі еселі интегралды есептеңіз. Шешуі .

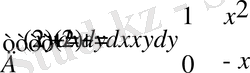
22-мысал:

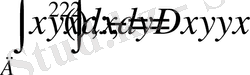
екі еселі интегралды есептеңіз. y

B

0 1 х

Сурет 13.

.

Демек сызықтар нүктелерінде қиылысады екен. Берілген қисықтарды салып облысын анықтаймыз.

.

23-мысал: екі еселі интегралды есептеңіз.

Шешуі: Берілген 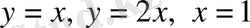қисықтарды салып (D) облысын анықтаймыз.

y

0 1 x

Сурет 14

1. 8 ЕСЕЛІ ИНТЕГРАЛДАРДЫ КОМПЬЮТЕР КӨМЕГІМЕН

ЕСЕПТЕУ

1. Екі еселі интегралдарды Int функциясының көмегімен есептеу

Maple жүйесінде екі еселі интегралдарды әр түрлі әдістермен есептеуге болады [10-13] . Бұл әдістердің ең қарапайымы int( ) функциясынан пайдалану. Бұл функцияны қолдану кезінде қосымша бұйрықтар және Maple жүйесінің библиотекасы қосылуы қажет емес.

Бұл функцияны қолдану үшін қарастырылатын екі еселі интеграл қайталанба түрге келтірілген болуы қажет .

24-мысал:

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.