Сұйықтардың қасиеттері

Қазақстан Республикасының білім және ғылым министрлігі

Қарағанды мемлекеттік техникалық университеті

Кафедра: Х және ХТ

КУРСТЫҚ

ЖҰМЫС (ЖОБА)

Пәні бойынша: Химия өндірістерінің негізгі прцестері мен аппараттары

Тақырыбы: Сұйықтықтың ағу ережелері

Жетекшісі:

(Бағасы) (Күні, қолы)

Студент: тобы

(Күні, қолы)

Қарағанды 2017

Мазмұны

КІРІСПЕ . . . 3

1. Сұйықтар туралы жалпы түсінік . . . 4

2. Сұйық ағыстарының түрлері: Ламинарлы және турбулентті ағыс . . . 5-7

3. Сұйықтың саңылау және саптамалар арқылы ағуы . . . 7

3. 1 Жіңішке қабырғалардағы кішкене саңылаулар арқылы тұрақты арында сұйықтықтың ағуы . . . 7-10

3. 2 Деңгейлік ағу . . . 10-11

3. 3 Тұрақты арында қондырма арқылы ағу . . . 11-15

3. 4 Сұйықтық ағынының қоршаған беттерге түсіретін қысымы . . . 15-16

4. Сұйықтардың құрылымы . . . 16-17

5. Сұйықтардың қасиеттері: Булану және конденсациялану . . . 17

ҚОРЫТЫНДЫ . . . 18-19

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ . . . 20

КІРІСПЕ

Курстық жұмыс өзектілігі. Біз бұл курстық жұмысты жаза отырып сұйықтардың негізгі қасиеттерін толықтай дерлік біле алатын деңгейге жетеміз. Біз сұйық ұғымын тек қана ғылымда ғана сонымен қатар өнеркәсіпте, тұрмыста да көптеп қолданамыз. Сондықтанда сұйықтар туралы толықтай зерттеу білу бізге көптеп көмегін тигізері сөзсіз. Егерде біз сұйықтардың негізгі қасиеттерін зерттемесек ғылымда кейбір нәрселер белгісіз болып қалар еді және сонымен қатар өнекәсіпте, тұрмыста қолайсыз жәйттардың орын алары мүмкін болар еді. Ұсынылып отырған зерттеудің негізгі өзектілігі де осында.

Зерттеу нысаны. Жұмысымызда сұйықтардың негізгі қасиеттеріне байланысты барлық жағдайларды зерттей, талдай отырып, осы сұйықтарға байланысты негізгі қасиеттерді қарастырып, сұйықтардың басқа да агрегаттық күйлермен салыстырғандағы айырмашылықтарына, ерекшеліктері мен айырмашылықтарын, түрлері мен олардың қасиеттеріне сондай-ақ сұйықтарда болатын құбылыстарға тоқталамыз.

Зерттеу жұмысының мақсаты мен міндеті. Жұмыстың мақсаты - сұйықтар туралы жан-жақты саралап, айқындап, сұйықтарға қатысты құбылыстардың барлығына дерлік зерттеулер нәтижелері арқылы көз жеткізу. Ол үшін мынадай мынадай міндеттер орындау көзделді;

• Сұйықтардың негізгі қасиеттері туралы мәселенің ғылыми-теорилық негіздерін анықтау;
• Сұйықтардың болмысын, түрлерін, негізгі белгілерін, ерекшеліктерін, құрылымын, қозғалысын, субъектілерін анықтау;
• Сұйықтардың басқа да физикалық құбылыстармен байланыстарын зерттеу, оларға сипаттама беріп, жіктеу;
• Сұйықтарда ғана орын алатын құбылыстарды кеңінен зерттеп жазу;

Зерттеу материалдары. Сұйықтардың негізгі қасиеттерін, түрлерін және басқа агрегаттық күйлермен салыстырғандағы салыстырғандағы ерекшеліктерін мен олардан айырмашылықтарын, қозғалыстағы қасиеттерін, күйлерін, белгілерін зерттеуде үлкен үлес қосқан қазақстандық ғалымдардың еңбектері. Олар мыналар: Ж. Абдулла, Т. Аязбаев, Ә. С. Асқарова, М. С. Молдабекова және тағы басқа ғаламтор ресурстары қолданылды.

1. Сұйықтық туралы негізгі түсініктер

Сұйықтық - сұйық агрегаттық күйдегі зат, газ бен қатты күйлердің арасындағы аралықты алып жатыр. Сұйықтықтың басқа агрегаттық күйлерден басты айырмашылығы - көлемін түрақты түрде сақтай отырып жанама күштердің әсерінен өзінің формасын шексіз түрде өзгерте алуы. Сұйықтық үлкен қысымда тұтқыр күйде кездеседі.

Сұйық дегеніміз ағатын қасиеті бар материал (орта) . Ағын - үзіліссіз деформацияланатын қозғалыст түрі. Қозғалыс әрине күш әрекетімен болады. Сұйық ағыны, өте аз күштің әсерімен, шексіз деформацияланатын тұтас ортаның көрінісі. Табиғаттағы заттың бәрі қатты, сұйық және газ күйінде кездеседі. Олардың молекулаларын қозғалу ерекшеліктері және молекулааралық күштері әртүрлі болады. Қатты заттардың молекулалары тұрақты орталықтарда тербеліс жасап тұрады. Ал газ молекулалары бір-бірімен соқтығысып, үздіксіз орын ауыстырып отырады. Сұйықтар белгілі жағдайда қатты зат күйіне де өте алады. Сондықтан он молекулалары лездік орталықта тербеліс жасап тұрып, секіріп басқа орталыққа ауыса алады. Сұйық молекулаларын осы қозғалу ерекшелігі сұйыққа аққыштық қасиет дарытады және кез-келген ыдыс формасын қабылдай алуын қамтамасыз етеді. Газ молекулаларын ара қашықтығы, сұйық немесе қатты дене молекулаларын ара қашықтығынан әлдеқайда көп, ал оның есесіне молекулааралық күштері өте аз. Сондықтан газдарды сығу оңай, сұйық пен қатты денелерді сығу қиын. Осы тұрғыдан қарағанда газдарды сығылатын сұйық, ал шынайы сұйықтарды сығылмайтын немесе өте аз сығылатын, тамшы құрайтын сұйық деп бөлуге болады. Гидравликада тек тамшы құрайтын сұйықтардың тыныштық күш мен қозғалыс сырларын қарастырады. Мұн ең төте жолы - сұйық табиғатын танытатын он моделін анықтау болып табылады. Ол сұйықт тұтастығы. Бұл модель бойынша, сұйық өзі алып тұрған кеңістікте, немесе қозғалып бара жатқан арнада біртұтас, арасында қуыс немесе бос орын жоқ деп есептелінеді. Сондықтан сұйықты сипаттайтын физикалық ұғымдарды үздіксіз функциялар және олардың дербес туындыларында да үздіксіз деп қарастыруға болады. Басқа сөзбен айтқанда, дифференциалдық және интегралдық есептеу тәсілдерін кеңінен пайдалануға жол ашылады. Бұл жорамалды бірінші болып Б. Кастелли ұсынған.

Табиғатта кездесетін сұйықтардың барлығы оларды немесе сығуға қарсылық көрсетеді, сондықтан оларды шынайы (тұтқырлы), немесе ньютондық сұйықтар деп атайды. Керісінше, сұйық қабаттарын өзара салыстырмалы қозғалысқа түсіретін күштерге ешқандай қарсылық көрсетпейтін сұйықты идеал (тұтқырлықсыз) сұйық деп атайды.

Идеал сұйықтың тығыздығы тұрақты, оған тек сыққыш күштеулер ғана әсер етеді. Табиғатта идеал сұйық жоқ, ол тек сұйық қозғалысын ерекшеліктерін зерттеуді оңайлататын модель ретінде пайдаланылады.

2. Сұйық ағыстарының түрлері: Ламинарлы және турбулентті ағыс.

Табиғатта сұйық қозғалыстың екі әртүрлі тәртібі бар екендігін бақылаудың нәтижесінен білеміз. Оның біріншісінде жекелей тарамдар бір-бірімен араласпай, параллель түрінде қозғалады. Сұйықтық бұлайша ағыстық бағытымен параллель күйінде қабаттар тәрізді араласа отырып белгілі бір тәртіппен қозғалысы ламинарлы ағыс деп атайды. Ал екінші жағыдайда, ағыс белгілі бір тәртіпсіз, олқы күйінде судың жылжуы. Сұйықтық құбырдың бойымен келіп түсуінің негізгі жолымен қатар, оның кей бөліктерінің айналып, араласа отырып заңсыз тәртіпте келуі де айқындалған. Сұйықтың мұндай тәртіпсіз жылжу түрі турбуленттік ағыс деп аталады.

Ламинарлы ағын (Поток ламинарный; лат. lamina - жолақ, қатпар ) - газ немесе тұтқырлы сұйықтықтың қатпарлы ағыны. Ламинарлы ағын сараптамада Рейнольде саны мәнімен өрнектеледі: R _c =VL/A, < R _c мұндағы V және L - берілген ағынның жылдамдығы (м/с), λ - кинематикалық сүйықтықтың тұтқырлығы (м ² /с), мысалы, ағын дөңгелек құбырда болса, L=d (құбырдың диаметрі) R _cкр = 2300 және орташа V=4λ _c /¶d ² , мұндағы λ _c - сұйықтықтың секунтдағы шығын көлемі (м ³ /с), Пуазелля заңдылығымен анықталады. Ламинарлық ағыс - сұйықтық-тың немесе газдың көрші қабаттары бір-бірімен араласпай, параллель ағатын тәртіптелген ағысы.

Ламинарлық ағыс өте тұтқыр сұйықтықта, едәуір аз жылдамдықпен қозғалатын сұйықтық ағысында, шағын мөлшердегі денелерді сұйықтық баяу жылдамдықпен орай аққанда пайда болады. Сондай-ақ, Ламинарлық ағыс жіңішке ( капиллярлық ) түтіктерде, мойынтіректерде ( подшипниктерде ), майлау кезінде пайда болған қабаттарда, сұйықтық не газ денені орай аққанда, дене беті маңында пайда болатын жұқа шекаралық қабаттарда, т. б. байқалады. Сұйықтық қозғалысының жылдамдығы артқан сайын, оның Ламинарлық ағысты белгілі бір кезеңде сұйықтық бөлшектері ретсіз қозғалатын турбуленттік ағысқа айналады. Сұйықтық ағысының режимі Рейнольдс санымен ( Re ) сипатталады. Re-нің шамасы, белгілі бір кризистік мәнінен ( Reкp ) кіші ( Re<Reкp ) болса, онда сұйықтық ағысының тәртібі ( режимі ) Ламинарлық ағысқа, ал Re>Rekp болса, онда сұйықтық ағысының тәртібі ( режимі ) турбуленттік ағысқа жатады. Сондықтан Re<2300 болғанда құбырдағы ағыс Ламинарлақ ағыс болып есептеледі. Тұтқыр Ламинарлақ ағыс кезінде құбырдағы сұйықтық шығыны Пуазәйль заңы бойынша анықталады.

Турбуленттік ағыс (лат. turbulentus - тәртіпсіз, долы) - сұйықтықтың немесе газдың әр нүктесінде уақыт өзгеруіне байланысты қозғалыс жылдамдығының мәні де, бағыты да өзгеріп, жылдамдығы тамырдың соғуына ұқсас сипатта өтетін ағыс.

Ешбір зандылықсыз қозғалған сұйық (газ) тамшыларының (ортаның өте шағын бөлшектерінің) бір-бірімен араласуы мейілінше қарқынды өтетін және сындарлы көрсеткіштен жоғары жылдамдықтармен қозғалған сұйық (газ) ағысы. Синонимі -"сұйықтың құйынды қозғалысы".

Турбуленттілік - сұйықтықтың соңғы массасының газ молекулаларына ұқсас ретсіз, бей-берекет, әр түрлі бағытта қозғалуы. Турбулентті қозғалыс кезінде сұйықтықтың бөлшектері өзара араласып, ағынның кез келген нүктесіндегі жылдамдық үнемі белгілі бір орташа мәннің айналасында және оның бағыты, шамасы бойынша да өзгеріп отырады. Бұл құбылыс - жылдамдық лүпілі, яғни турбуленттілік қозғалысының шын мәніндегі бірқалыпсыз қозғалысы, өйткені оның жылдамдығы үздіксіз әрі үнемі уақыт бойынша ешбір зандылыққа бағынбай өзгеріп отырады. Қарастырылып отырған уақыт мезгіліндегі турбуленттік ағыс механизмі күрделі жылдамдықтың мұндай ретсіз өзгеруі ағындының бір нүктесінен екінші нүктесіне көшу кезінде де байқалады. Турбуленттік ағыстағы сұйық - бөлшектерінің қарқынды араласуы және сұйық бөлшектері қозғалыс траекториясының күрделілігімен түсіндіріледі. Сол қозғалыс үстінде олар ағынның бағытынан күрделі траектория бойынша ауытқып отырады. Жьлдамдық пен қысым лүпілі, яғни ағынның әр нүктесінде болып отыратын үздіксіз өзгеріс сұйықтықтың турбуленттілік қозғалысының өзіне тән ерекшелігі ретінде түсіндіріледі. Бұл лүпілдер белгілі бір мөлшерде кездейсоқ сипатқа ие. Жылдамдықтың лүпілдік өзгерісін оның бағыты бойынша өзгеріп отыратын нүктенің уақыт бойынша орташаланған жылдамдығына үстеме ретінде қарастыруға болады. Лүпілдік қозғалыс сұйықтардың іргелес қабаттарының араласуын немесе турбулентті араласу проңесін тудырады. Турбуленттілік лүпіл жиілігі бойынша ажыратылады:

1) жиілігі төмен лүпілдер сызықтық өлшемі ағын тереңдігімен бірдей немесе одан да артық турбуленттік ағынмен қозғалатын анағұрлым ірі құйындар туғызады;

2) жиілігі жоғары лүпілдер кіші құйындардың таралуына байланысты, соңғысы ірі құйындардың ішінде болады және олардың арасындағы бос кеңістікті толықтырады.

Егер ағынның барлық нүктелеріндегі жылдамдық өрісінің орташаланған барлық сипаттамалары бірдей болса, онда турбуленттілік ағыс біртекті деп аталады. Басқаша айтқанда, біртекті турбуленттілік ағыс барлық нүктелердің бірдей жағдайда болуымен сипатталады. Егер жылдамдықтар арасындағы корреляция коэффициенті координатор жүйесін кез келген бағытқа бұрған кезде де өз мәнін сақтап қалатын болса, онда турбуленттілік ағыс изотронды деп аталады. Изотронды турбуленттілік ағыс әр түрлі бағыттардың тепе-тендігімен әрі басым бағыттардың жоқтығымен сипатталады. Сұйықтықтың турбулентті қозғалысы кезінде ағын мынадай екі аймақпен сипатталады:

1) меншікті турбулентті режім;

2) үйкеліс күшінің қатысуымен құйын тудырып, ағынның барлық қабатына таралатын, қабырғаға тікелей жанасатын шекаралық аймақ.

Шекаралық аймақты турбуленттік қозғалысқа Рейнольде санының ықтимал мәнінде жүзеге асырады.

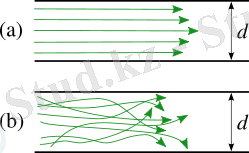
Ламинарлық (а) және турбулентті (b)

3. Сұйықтың саңылау және саптамалар арқылы ағуы

Сұйықтықтың резервуарлардан, бактардан, қазандықтардан саңылаулар мен қондырмалар арқылы (әр түрлі формадағы қысқа құбырлар) атмосфераға немесе газбен немесе дәл сол сұйықтықпен толтырлған кеңістікке ағуын қарастырайық. Осындай ағу процесі кезінде резервуардағы сұйықтықтық ие болатын потенциалдық энергия қоры еркін ағыстың кинетикалық энергиясына айналады.

Аталған жағдайдағы қызықтыратын негізгі мәселе саңылаулар мен саптамалар үшін ағу жылдамдығы мен сұйықтық шығынын анықтау болып табылады.

3. 1 Жіңішке қабырғалардағы кішкене саңылаулар арқылы тұрақты арында сұйықтықтың ағуы

Ішінде Р ₀ қысымдағы сұйықтығы бар, қабырғасында еркін бетінен жеткілікті деңгейдегі Н ₀ тереңдікте кішкене дөңгелек саңылауы бар үлкен (7. 1- сурет) .

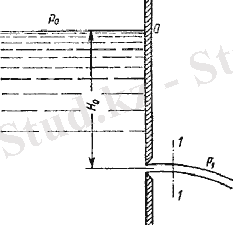
Cурет 7. 1- Резервуардан кішкене саңылау арқылы ағу

Сұйықтық қысымы Р ₁ болатын ауа кеңістігіне ағады. Саңылау 7. 2 а) суретте көрсетілгендей қалыпта, яғни, жіңішке қабырғаға кіру жиегін өңдеусіз бұрғылап тесу түрінде немесе 7. 2 б) суреттегідей, яғни, қалың қабырғада, бірақ, кіру жиегін сыртқы жағынан үшкірлеу арқылы жасалған болсын. Ағын саңылау жиегінен ажырағанда біраз сығылады (7. 2 а сурет) . Мұндай сығылу сұйықтықтың әр түрлі бағыттардан қозғалысына, оның ішінде қабырға бойымен тарамдалған қозғалыстан, ағындағы остік қозғалысқа дейін қозғалыстармен түсіндіріледі.

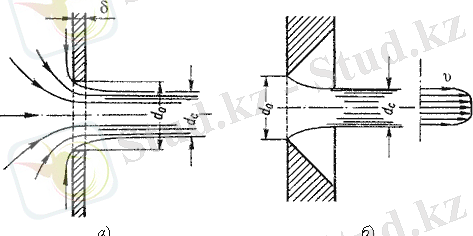
Cурет 7. 2 - Дөңгелек саңылау арқылы ағу

Сығылу дәрежесі сығылу коэффициентімен бағаланады.

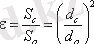
мұнда: Sс және Sо - сәйкесінше ағын мен саңылаудың көлденең қималарының аудандары;

dс және dо - ағын мен саңылаудың сәйкес диаметрлері.

Мұндай саңылау арқылы сұйықтың ағу жылдамдығы

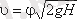
мұнда: Н - сұйықтық арыны, былай анықталады

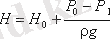
φ- жылдамдық коэффициенті:

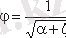
мұнда: α-Кориолис коэффициенті;
ζ- саңылаудың кедергі коэффициенті.

Сұйықтық шығыны іс жүзіндегі ағу жылдамдығының нақты қима ауданына көбейтіндісімен анықталады:

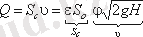
ε және φ көбейтіндісін μ әрпімен белгілеу және шығын коэффициенті деп атау қабылданған, яғни, μ = εφ. Нәтижесінде шығынды аламыз:

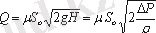
мұнда: ΔР - әсерінен ағу жүретін қысымдардың есептік айырымы.

Осы өрнектің көмегімен негізгі есеп шешіледі - шығын анықталады. Дөңгелек саңылау үшін сығылу ε, кедергі ζ, жылдамдық φ және шығын μ коэффициенттерінің мәнін эмпирикалық тұрғызылған тәуелділіктер арқылы анықтауға болады. (7. 3 суретте) идеал жылдамдық үшін есептелінген ε, ζ және μ коэффициенттерінің Рейнольдс санына тәуелділігі көрсетілген:

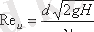
мұнда: ν - кинематикалық тұтқырлық.

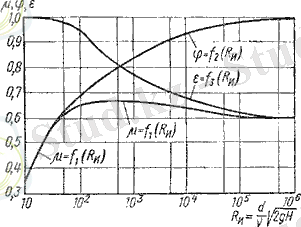
Сурет 7. 3- ε, ζ және μ - дің Re _u санына тәуелділігі

Жіңішке қабырғадағы кішкене саңылаудан ағынның атмосфераға ағуы кезінде, ағын инверсиясы (7. 4 сурет) деп аталатын, ағынның оның ұзындығы бойынша өзгеруі жүреді. Бұл құбылыс, негізінен, ағып жатқан қисық сызықты ағыншаларға әсер ететін беттік керілу күштерімен және саңылау периметрі бойынша әр түрлі жағдайларға байланысты түсіндіріледі. Инверсия бәрінен бұрын дөңгелек емес саңылаулардағы ағу кезінде байқалады.

Жіңішке қабырғадағы кішкене саңылаудан ағынның атмосфераға ағуы кезінде, ағын инверсиясы (7. 4 сурет) деп аталатын, ағынның оның ұзындығы бойынша өзгеруі жүреді. Бұл құбылыс, негізінен, ағып жатқан қисық сызықты ағыншаларға әсер ететін беттік керілу күштерімен және саңылау периметрі бойынша әр түрлі жағдайларға байланысты түсіндіріледі. Инверсия бәрінен бұрын дөңгелек емес саңылаулардағы ағу кезінде байқалады.

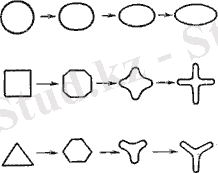
Сурет 7. 4 - Ағын инверсиялары

3. 2 Деңгейлік ағу

Сұйықтықтың атмосфераға емес, дәл осы сұйықтықпен толтырылған кеңістікке ағуы іс жүзінде жиі кездеседі (7. 5- сурет) . Мұндай жағдай деңгейлік ағу немесе су басып кеткен саңылаумен ағу деп аталады.

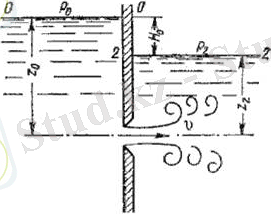
Сурет 7. 5- Деңгейлік ағу

Бұл жағдайда ағынның барық кинетикалық энергиясы кенеттен ұлғаю кезіндегі сияқты құйын түзілуге шығындалады.

Ағынның сығылған қимасындағы жылдамдық

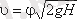
мұнда: φ - жылдамдық коэффициенті;
Н -есептік арын.

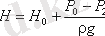
Сұйықтық шығыны мынаған тең

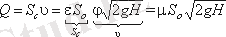
Сонымен, ауаға (газға) ағу кезіндегідей есептеу формулаларын аламыз, тек қана есептік арын Н берілген жағдайда екі қабырғасы бойынша гидростатикалық арындардың айырымы түрінде болады, яғни, аталған жағдайда сұйықтық жылдамдығы мен шығыны саңылаудың орналасу биіктігіне тәуелді емес.

Деңгейлік ағу кезінде сығылу мен шығын коэффициенттерін ауалық ортаға ағу кезіндегідей қабылдауға болады.

3. 3 Тұрақты арында қондырма арқылы ағу

Сыртқы цилиндрлік қондырма деп кіру жиегінің дөңгелектеуінсіз ұзындығы бірнеше диаметрге тең қысқа құбыршаны айтады (5. 7 сурет) . Практикада мұндай қондырма қалың қабырғаны бұрғылап тескенде және кіру жиегін өңдемеген кезде жиі көрініс табады. Осындай қондырма арқылы газдық ортаға ағу екі режимде жүруі мүмкін.

Бірінші режим - үздіксіз режим. Ағу кезінде ағын қондырмаға кіргеннен кейін, жіңішке қабырғадағы саңылау арқылы ағу кезіндегіге ұқсас сығылады. Содан соң ағын саңылау өлшеміне дейін біртіндеп ұлғаяды да, қондырмадан толық қимамен шығады (7. 6- сурет) .

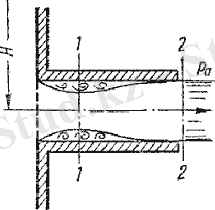
Сурет 7. 6- Қондырма арқылы ағу

Қондырманың салыстырмалы ұзындығы l / d мен Рейнольдс санына тәуелді шығын коэффициенті μ мына эмпирикалық формуламен анықталады:

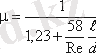
Қондырмадан шыққан кездегі ағын диаметрі саңылау диаметріне тең болғандықтан, сығылу коэффициенті ε = 1 және бұдан шығатыны, μ = φ, ал кедергі коэффициенті ζ = 0, 5.

Егер 1-1 сығылған қима мен қондырмадан кейінгі 2-2 қимасы үшін Бернулли теңдеуін құрып және оны түрлендірсек, қондырма ішіндегі қысымның төмендеуін алуға болады

Белгілі бір Нкр кризистік арында қондырма ішіндегі (1-1 қимасы) абсолют қысым нөлге тең болып кетеді (P1 = 0), сондықтан

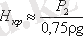
Бұдан шығатыны, Н > Н _кр болғанда P ₁ қысым теріс мәнге ие болуы керек, бірақ сұйықтықтарда теріс қысымдар болмайтындықтан, бірінші қозғалыс режимі мүмкін емес болып шығады. Сондықтан Н Н _кр болғанда ағу режимінің өзгеруі, бірінші режимнен екінші режимге өту жүреді (7. 7- сурет) .

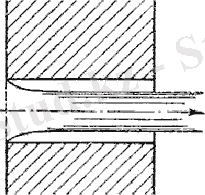
Сурет 7. 7- Қондырма арқылы ағудың екінші режимі

Екінші режим ағынның сығылудан кейін ұлғаймай, цилиндрлік формасын сақтап және қондырма ішінде, оның қабырғаларына жанаспай орын ауыстыруымен сипатталады. Ағу жіңішке қабырғадағы саңылаудағы сияқты, дәл сондай коэффициент мәндерінде болады. Яғни, бұдан шығатыны, бірінші режимнен екінші режимге өткенде жылдамдық артады, ал шығын ағынның сығылуына орай азаяды.

Цилиндрлік қондырмадан деңгейлік аққанда ағудың бірінші режимінің жоғарыда суреттелгендегіден айырмашылық болмайды. Бірақ Н > Н _кр болғанда екінші режимге өту жүрмейді, кавитациялық режим басталады.

Осылайша, сыртқы цилиндрлік қондырма айтарлықтай кемшіліктерге ие: бірінші режимде - үлкен кедергі және шығын коэффициентінің жеткілікті дәрежеде жоғары болмауы, ал екінші режимде - өте төмен шығын коэффициенті. Кемшілігінің қатарына осылармен бірге деңгейлік ағу кезіндегі кавитацияның болу мүмкіндігі саналады.

Сыртқы цилиндрлік қондырманы кіру жиегін дөңгелектеу немесе конустық кіріс орнату жолымен айтарлықтай жақсартуға болады. 7. 8- суретте әр түрлі қондырма түрлері және сәйкес коэффициенттер мәндері көрсетілген.

Сурет 7. 8- Сұйықтықтың қондырмалар арқылы ағуы а - конустық ұлғаятын; б - конустық кішірейетін; в - коноидалы; г - ішкі цилиндрлік.

Конустық қосылатын және коноидалы қондырмалар энергияны аз жоғалта отырып салыстырмалы түрде үлкен ұзындықтағы, жақсы ықшам ағынды алу керек жерлерде (арындық брандспойттарда, гидромониторларда және т. б. ) қолданылады. Конустық қосылатын қондырмалар шығу жылдамдықтары аз кезде ағу шығынын арттыру үшін пайдаланылады.

Атмосфераға ашылған ыдыстың ағыс орнықпаған кезде, тұрақты кемитін арында босауын қарастырайық (7. 9- сурет) .

Алайда, егер арын, ал бұдан шығатыны ағу жылдамдығы да жай өзгереді, онда әрбір уақыт мезетіндегі қозғалысты орныққан деп қарастыруға және есепті шешуге Бернулли теңдеуін қолдануға болады.

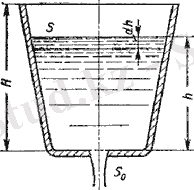
Сурет 7. 9- Резервуардың босау сызбанұсқасы

Ыдыстағы сұйықтық деңгейінің өзгермелі биіктігін h, осы деңгейдегі резервуар қимасының ауданын S, саңылау ауданын Sо деп белгілеп және шексіз аз dt уақыт аралығын алып келесі көлем теңдеулерін жазуға болады:

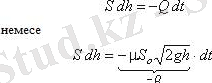
мұнда: dh - dt уақыт аралығындағы сұйықтық деңгейінің өзгеруі.

Осыдан биіктігі Н ыдыстың толық босау уақыты

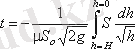
Егер S ауданның h биктік бойынша өзгеру заңдылығы белгілі болса, онда интегралды есептеуге болады. Призмалық ыдыс үшін S = const (7. 10- сурет), бұдан шығатыны, оның толық босау уақыты

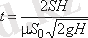
Бұл теңдеуден призмалық ыдыстың толық босау уақыты бастапқысына тең тұрақты арындағы тура сондай сұйықтық көлемінің ағу уақытынан екі есе көп.

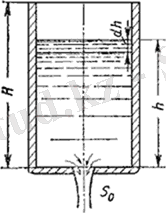
Cурет 7. 10- Резервуардың босау сызбанұсқасы

Горизонталь цилиндрлік ыдыстан (цистернадан) (7. 11- сурет) сұйықтықтың ағу уақытын анықтау үшін S айнымалы ауданның h -қа тәуелділігін өрнектейік:

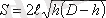
мұнда: l - цистернаның ұзындығы;

D - цистернаның диаметрі.

Сол кезде осындай цистернаның толық босау уақыты, яғни, арынның h1 = D -дан h2 = 0-ге дейінгі өзгеруі мынаған тең

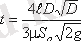
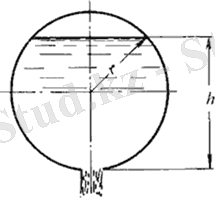
Cурет 7. 11- Призма түрінде емес резервуардың босауы

3. 4 Сұйықтық ағынының қоршаған беттерге түсіретін қысымы

Егер саңылау немесе саптама арқылы ағатын ағын қозғалмайтын қабырғаға түссе, онда ол белгілі бір қысыммен оған әсер етеді. Ағынның алаңшаға түсіретін қысымы есептелетін негізгі теңдеу келесі түрге ие:

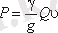
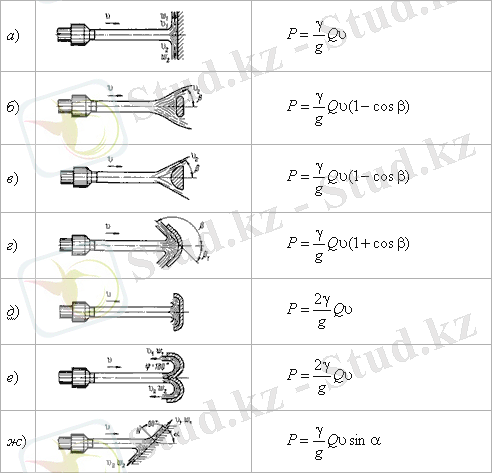
7. 12- суретте практикада неғұрлым жиі кездесетін қоршайтын беттер (бөгеттер) мен ағынның сәйкес бетке түсіретін қысымы есептелетін теңдеулер келтірілген.

Ағын қысымының шамасы, әрине, қондырма мен бөгеттің арақашықтығына тәуелді. Ара қашықтықтың артуымен ағын ыдырайды және қысым төмендейді. Осыған сәйкес зерттеулер берілген жағдайда ағын үш сипаттық бөлікке бөлінетінін көрсетеді: ықшам тұтас, бөлшектенген және шашыранды.

Ықшам тұтас бөлігінің шегінде ағынның цилиндрлік формасы қозғалыстың тұтастығын бұзбастан сақталады. Бөлшектенген бөлігінің шегінде ағыс тұтастығы бұзылады, мұнымен қоса ағын біртіндеп ұлғаяды. Соңғысы ағынның шашыранды бөлігінің шегінде ағыстың толығымен жекелеген тамшыларға ыдырауы жүреді.

... жалғасы

Сұйықтар. Сұйық құбылыстары

Сұйықтар,қатты денелер

Азық-түлік өнімдерінің реологиясы

Сұйықтар мен газдардың қозғалыстарын зерттеу мәселелері

Полимерлі материалдардың реологиясы және жылуфизикалық қасиеттерін зерттеу

Сұйықтар. Қатты денелер туралы ақпарат

Фармацевтикалық химияның міндеттері

Көмір сутекті газдарды тазалаудың технологиялық параметрлерін автоматты бақылау

Сұйықтықтың физикалық қасиеттері

Сұйықтар мен қатты денелердің қасиеттері

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс