Кешігуі бар буыны

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 11 бет
Таңдаулыға:

Қазақстан Республикасы Білім және ғылым министрлігі

Шәкәрім университеті

СӨЖ

Тақырыбы: Буындардың түрлері және реттеу заңдары

Орындаған: Әбдікәрім Ә

Топ: АУ-601

Тексерген: Секербаева А. Б.

Семей 2018

Жоспар:

Кіріспе

Инерциясыз (күшейткіш) буын
Инерциялы буын
Тербелмелі буын
Интегралды буын
Дифференциалдаушы буын
Кешігуі бар буыны
Реттеуіштер

Қорытынды

Пайдаланылған әдебиеттер

Кіріспе

Автоматты реттеу жүйелері әр түрлі жолмен оларды құрайтын жеке элементтерге бөлінуі мүмкін. Тәсілдердің бір түріне жүйе тағайындалуы бойынша, функционалды белгісі бойынша жеке элементтерге жіктеледі, мысалы реттеу объектісі, басқарушы элемент, орындаушы механизм және т. б. ажыратылады.

Жүйені конструктивті рәсімделуі бойынша элементтерге жіктеуге болады (мысалы, генератор, электромашиналы күшейткіш, потенциометр) .

Дегенмен автоматты реттеу жүйесінің төзімділігі мен сапасын зерттеу кезінде элементтерді олардың динамикалық қасиеттері бойынша бөлу маңызды. Жүйе элементтерін осындай негізде қарастыру, әр түрлі әрекет ету принциптері мен әр түрлі конструктивті рәсімделуі бар түрлі элементтер бірдей дифференциалды теңдеумен сипатталады, демек бірдей динамикалық қасиеттерге ие және өтпелі процесс кезінде өзін-өзі ұстауы да бірдей болады.

Өзінің динамикалық қасиеті жағынан қарастырылатын элемент буын деп аталады. Шоғырланған параметрлері кез келген сызықтық жүйе осындай қарапайым жай элементтерге бөлінуі мүмкін. Буынның өтпелі процестері қарапайым дифференциалды теңдеулермен бейнеленеді, олардың әрқайсысының реті екіден жоғары емес. Автоматты реттеу жүйесінің барлық нақты элементтері бөліне алатын үзбелер типінің саны онша үлкен емес. Төмендегідей буындарды ажыратуға болады: күшейткіш, апериодты, тербелістік, интегралдаушы, дифференциалдаушы, кешігу.

Инерциясыз (күшейткіш) буын

Инерциясыз буын деп шығыс шамасы кіріс шаманы еш бөгетсіз және кешіктірмей көрсететін буынды айтамыз:

X _шығ = k Х _кір , (1) мұндағы k - буынның күшею коэффициенті (беріліс коэффициенті) .

Күшейткіш буынды кейде қатаң байланыс деп атайды. Өтпелі процесс күшею үзбесінде болмайды. Күшейткіш буынның мысалдары: қатты рычак, инерциясыз электронды күшейткіш, электр машинасы бөлшектерінің механикалық жіктелуі. (1) өрнегінен күшейткіш буынның беріліс функциясы:

W(p) =X _шығ / Х _кір =k (2)

Амплитуда-фазалық жиілікті сипаттаманың (АФЖС) теңдеуі: W (jw) = k (3)

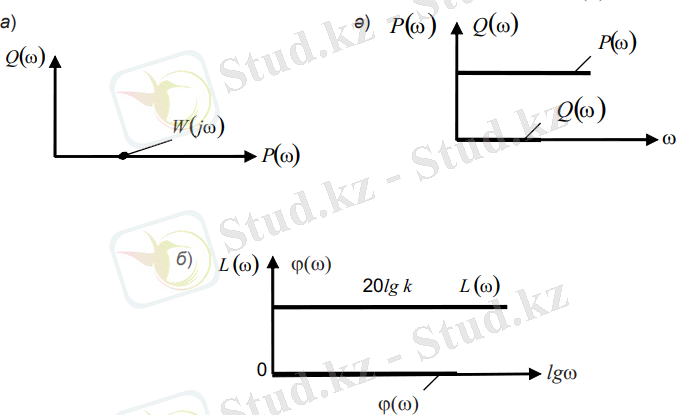
$C:\Users\компьютер\Pictures\Безымянный.png$

1-сурет. Инерциясыз буынның жиіліктік сипаттамалары

2. Инерциялы буын

Инерциялы буын деп бірінші ретті буынды айтамыз, кірісіне сатылы әсерді берген кезде шама апериодты түрде (экспоненция заңы бойынша) жаңа орнатылған мәнге ұмтылады. Сонымен қатар, мұндай буынды инерциялы, статикалық, релаксациялы, бір сыйымдылықты деп атайды.

Апериодты буындарға сыйымдылық пен активті кедергіден тұратын электр тізбегі (сыйымдылықсыз), массасы мен үйкеліс күші бар (серіппесіз) немесе серіппе мен үйкеліс күшінен (массасыз) тұратын механикалық құрылғылар және энергияның кез келген түрі жинақтала алатын және оны тарата алатын басқа да ұқсас құрылғылар жатады.

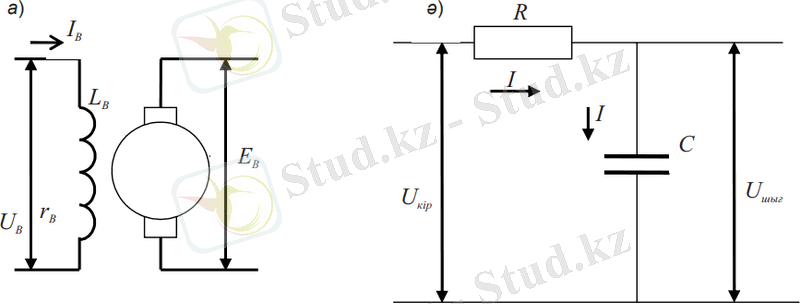
$C:\Users\компьютер\Pictures\Безымянный2.png$

2-сурет. Инерциялы буын мысалдары

3. Тербелмелі буын

Тербелмелі деп (екі сыйымдылықты) екінші ретті буын аталады, оның кірісіне сатылы әсерді берген кезде, шығыс шама өшіп-жанатын тербеліс жасай отырып, жаңа орнатылған мәнге ұмтылады.

Тербелмелі буындарға екі энергетикалық сыйымдылықтар арасындағы энергиямен алмасып, өтпелі режимдер ағып өтетін құрылғылар кіреді, мысалы, индуктивтілік, сыйымдылық және активті кедергіден құралған электр тізбегінен тұрады, массасы, серіппесі және (3. 1, а-сурет) үйкеліс күші бар механикалық құрылғы; кинетикалық энергияны якорьда және электрмагнитті энергияны магнитті тізбекте жинақтай алатын тәуелсіз әсерлі тұрақты токтың элекр қозғалтқышы, оның кіріс шамасы якорьға қосылған кернеу, ал (3. 1, ә-сурет) шығыс - якорьдың айналу жылдамдығы болып табылады.

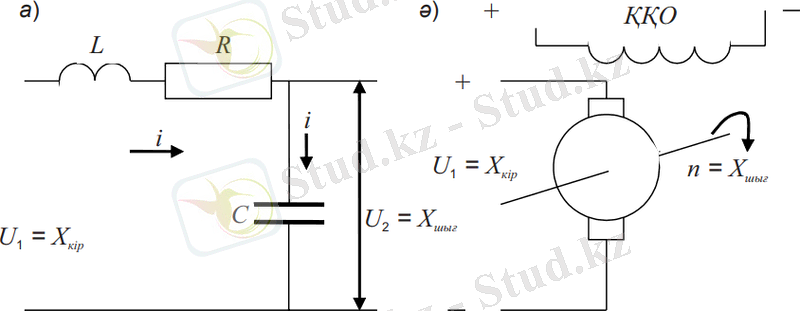
$C:\Users\компьютер\Pictures\Безымянный3.png$

3. 1-cурет. Тербеліс буын мысалдары. а - активті кедергісі, индуктивтілігі және сыйымдылығы бар тізбек; ә - тәуелсіз әсерлі тұрақты ток қозғалтқышы

$C:\Users\компьютер\Pictures\Безымянный4.png$

3. 2-cурет. Тербелмелі буынның жиіліктік сипаттамалары

4. Интегралды буын

Интегралды буын деп шығыс шаманың өзгеру жылдамдығы кіріс шамаға пропорционал немесе шығыс шамасы сол шаманың уақыт бойынша интегралына пропорционал болатын буынды айтамыз. Мұндай буынды, сонымен қатар астатикалық немесе бейтарапты буын деп айтады. Идеалды және шынайы интегралдауы буындар деп ажыратылады.

Идеалды интегралдаушы буынға тәуелсіз әсердегі тұрақты токтың электрлі қозғалтқышы мысал бола алады, егер кіріс шама ретінде UЯ якорьдың кернеуін, ал шығысы деп якорьдың бұрылу бұрышы α, егер электрмеханикалық және электрмагнитті уақыт тұрақтылары салыстырмалы түрде аз және оларды ескермеуге болады (4, а-сурет) .

Басқа мысал болып, егер қоректену құбырдағы сұйықтың жылдамдығы лезде орнықты мәнге жеткен кезде кіріс шама деп Q сұйық ағынын, ал шығысы деп резервуардағы сұйықтың деңгейін санағанда сұйық келіп түсетін резервуар табылады (4, а-сурет) .

Көбінесе тәжірибелік есептеулердің жеткілікті дәлдігі бойынша шынайы интегралдаушы буындардың орнына идеалды буындарды қабылдауға болады.

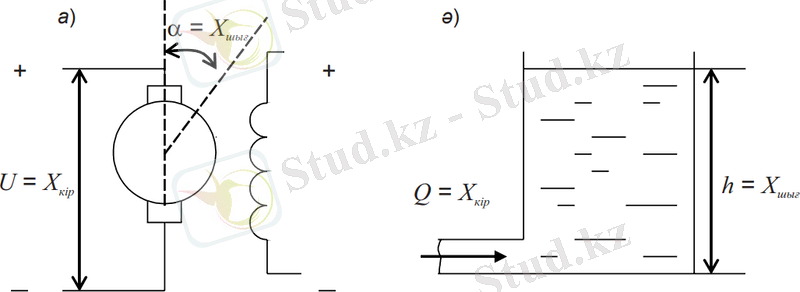
$C:\Users\компьютер\Pictures\Безымянный5.png$

4. 1-сурет. Интегралды буынның мысалдары

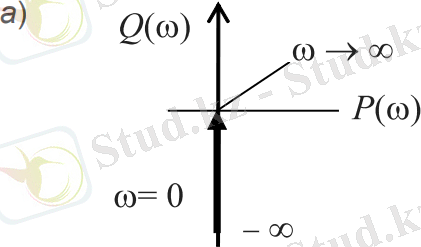
$C:\Users\компьютер\Pictures\Безымянный6 - копия.png$ $C:\Users\компьютер\Pictures\Безымянный6.png$

4. 2-сурет. Идеалды интегралды буынның жиіліктік сипаттамалары

5. Дифференциалдаушы буын

Дифференциалдаушы буын деп шығыс шама кіріс шаманың өзгеру жылдамдығына пропорционал, яғни оның туындысына пропорционал буынды айтамыз.

Дифференциалдаушы буындарға мыналар мысал бола алады: серіппелі гидравликалық тыныштандырғыш (5. 1, а-сурет), трансформатор (5. 1, ә-сурет), активті кедергісі мен сыйымдылығы бар тізбек (5. 1, б-сурет), активті кедергі мен индуктивтілігі бар тізбек (5. 1, в-сурет) .

Идеалды дифференциялдаушы буындар деп жоғарыда қарастырылған барлық құрылғыларды санауға болады, егер онда активті электрлі кедергілер мен үйкеліс күштерімен елемеуге болса (механикалық құрылғыларда) .

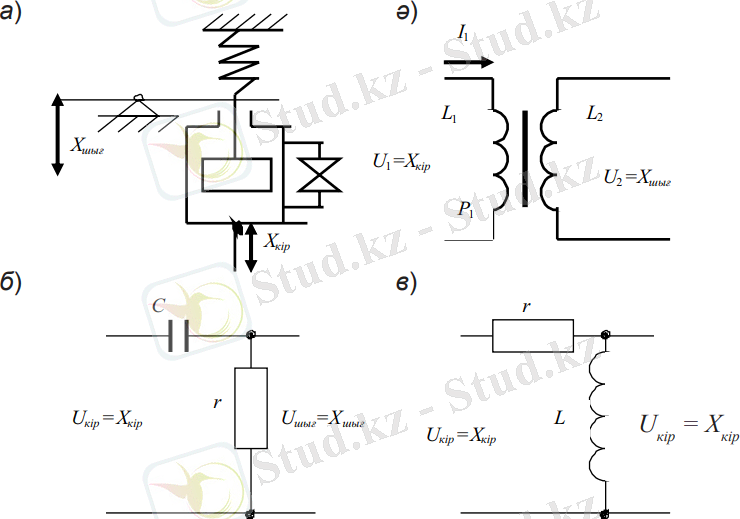
$C:\Users\компьютер\Pictures\Безымянный7.png$

5. 1-сурет. Дифференциялдаушы буынның мысалдары

Кірісіне сатылы әсерді берген кезде шығыс шаманың өзгерісі мен өтпелі функциясы келесі түсініктерден анықталуы мүмкін. Сатылы кіріс функция, үзіліс сияқты дифференциялданбайды, бірақ кіріс шаманы сатыдағы өзгеріс жылдамдығы шексіздікке тең, өйткені кіріс шаманың соңғы өзгеруі нөлге ұмтылатын уақыт шегінде жүреді. Ал дифференциялдаушы үзбенің шығыс шамасы кірістің өзгеру жылдамдығына пропорционал болғандықтан, идеалды буындағы кірісіне сатылы әсер берген кезде шығыс шамасы нөлге тең уақыт моментінде шексіздікке дейін шолп береді, ал содан кейін нөлге айналады, өйткені кіріс шаманың өзгеру жылдамдығы барлық тізбекті моменттерде нөлге тең болады (5. 2-сурет) .

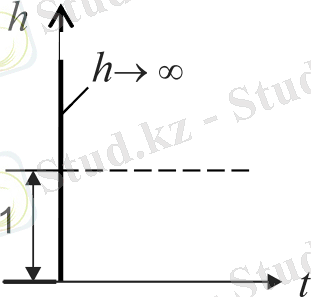
$C:\Users\компьютер\Pictures\Безымянный8.png$

5. 2-сурет. Идеалды дифференциялдаушы буынның өтпелі процесінің графигі

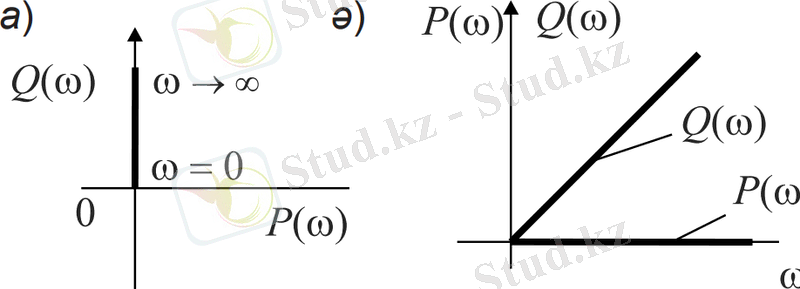
$C:\Users\компьютер\Pictures\Безымянный9.png$

5. 3-сурет. Идеалды дифференциялдаушы буынның жиілікті сипаттамалары

6. Кешігуі бар буыны

Кешігуі бар буын деп шығыс шама кіріс шаманың өзгерісін еш бөгетсіз, бірақ кейбір тұрақты t кешіктірумен жүргізетін буынды айтамыз (6-сурет) .

Кешігу буынына бір ұшымен жүктелетін конвейер мысал бола алады, ал жүктемені жүктелу пунктінен біршама арақашықтықта орналасқан конвейерлік таразымен өлшейді. Конвейерге келіп түсетін материалдың мөлшерінің өзгерісі таразылармен сол өзгерген сәтте емес, материалдың жүктелу пунктінен конвейерлік таразыларға орнын ауыстыру үшін қажетті біршама уақыт өткеннен кейін тіркеледі. Кіріс шама шығысқа тек қана уақыт бойынша қалып қойып, еш бөгетсіз беріледі. Мұндай кешігуді таза немесе транспорттық кешігу деп атайды.

Таза кешігу құбылысы тармақталған тұрақтылары мен элементтері бар және сигналдың соңғы өту жылдамдығы (мысалы, ұзын құбырлар) бар автоматты реттеу жүйелерінде орын алуы мүмкін.

Көп құбырлардағы кірістен шығысқа беру кезіндегі әсер бірнеше уақыт аралығында кешігіп қалады және түрі бойынша бұрмаланады. Бұл шар тәрізді диірмендерде, бу қазандарында және автоматты реттеудің басқа технологиялық объектілерінде жүруі мүмкін. Мұндай құрылғыларды көп жағдайларда екі буыннан тұратын кешігусіз буын және кешігуші буын деп қарастыруға болады.

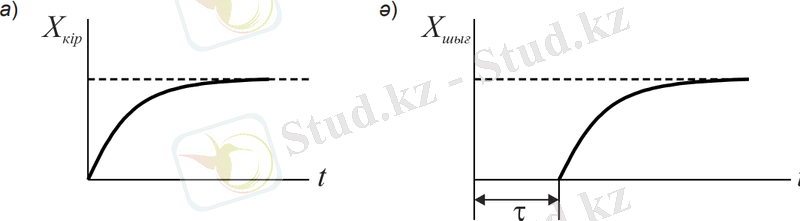
$C:\Users\компьютер\Pictures\Безымянный10.png$

6. 1-сурет. Кешігуі бар буынның өтпелі процесі: а - кіріс шаманың өзгерісі; ә - шығыс шаманың өзгерісі

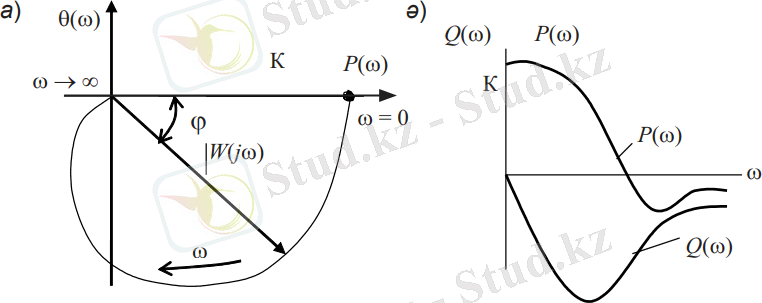
Кешігуі бар буынның анықтамасына Х _кір кіріс шамасы мен Xшығ шығыс шама арасындағы тәуелділікті аламыз. Х _шығ (t) = X _кір (t-t), (3) мұндағы t - таза кешігу уақыты. Нөлдік бастапқы шарттардағы операторлық түрдегі теңдеуді кешігу теоремасын пайдалана отырып аламыз. Х _шығ = X _кір е ^-τp . (4)

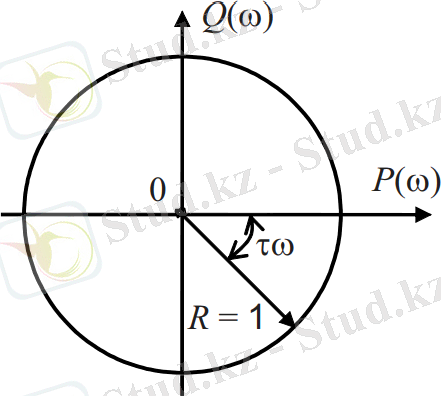
$C:\Users\компьютер\Pictures\Безымянный11.png$

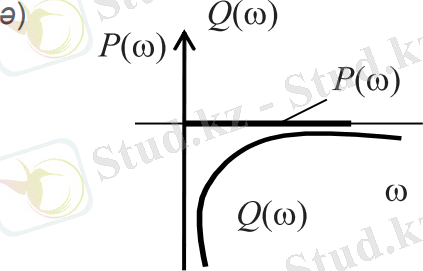
6. 2-сурет. Кешігуі бар буынның амплитуда-фазалық сипаттамасы

7. Реттеуіштер

Автоматты реттеуiштер мен реттелу объектiсi қосылып АРЖ-ны құрайды. Автоматты реттеуiштер деп реттелетiн шаманы берiлген деңгейде белгiлi бiр дәлдiкпен ұстап отыратын құрылғылар жиынтығын айтады.

Реттеуiштің кiрiсiне реттелетiн шаманың нақты 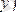және берiлген мәндерi 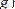келiп түседi (7. 1, а-сурет) . Олардың арасындағы айырымы реттеуiштiң шығыстық шамасының өзгерiсін тудырады:

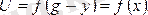(7. 1)

Автоматтандыру жүйесiндегі реттеуiштiң негiзгi міндетi реттеу қатесін анықтап, реттеушi ықпалды тудыру болып табылады. Реттеуiш элементтерiнiң инерциялығын ескермегендегi кiрiстiк және шығыстық шамалардың арасындағы тәуелділік реттеу заңын тұжырымдайды.

Қазіргі автоматтық жүйелерге қосымша талаптар қойылуда:

- екпінсіз ауысу ( тізбекте қосымша өтпелі үрдіссіз) қолмен басқарудан автоматты басқаруға және керсінше;

- автоматты басқару режимінде қорек көзінің сыртқы режимінен ішкі режимге екпінсіз өтуі;

- шығыс аналогты сигналдың төменгі және жоғары деңгейі бойынша шектелуі;

- кіріс және шығыс сигналдың гальваникалық бөлінуі;

- УВМ жоғары деңгейімен байланысы;

- адаптивті басқару жүйесін құруға қажетті аналогті және дискретті сигналдарды реттеу.

Автоматты реттегіштер тағайындалуы, әрекет принцпі, конструктивті ерекшелігі, пайдаланылатын энергия түріне т. б. байланысты бөлінеді.

Конструкциясы бойынша: аппаратты, құрылғылы, агрегатты, модульді.

Аппаратты типті реттеуіштер алғашқы өлшегіш түрлендіргіштермен кешенді жұмыс жасайтын құрылғылар. Бұндай типті реттегіштер технологиялық параметрлерді өлшеу құрылғыларынан тәуелсіз жұмыс жысайды.

Құрылғы типті реттегіштер екінші өлшегіш түрлендіргіштермен кешенді жұмыс жасауға арналған. Құрылғы типті реттегіштер алғашқы өлшегіш түрлендіргіштермен тікелей байланысы жоқ.

Агрегатты принцп бойынша тұрғызылған автоматты реттегіштер анықталған функцияларды орындайтын бөлек блоктардан тұрады. Кіріс және шығыс сигналдары бірыңғайланған.

Модульді принцип бойынша тұрғызылған автоматты реттегіштер қарапайым операцияларды орындайтын бөлек модульдерден тұрады. Модульдердің кіріс және шығыс сигналдары бірыңғайланған.

Қолданылатын энергия түріне байланысты реттегіштер электрлік (электромеханикалық, электронды), пневматикалық, гидравликалық және құрамданған (электропневматикалық, электро-гидравликалық және т. б. ) .

Реттегішті пайдаланатын энергия түріне байланысты таңдау реттеу объектісінің сипаты мен автоматты жүйенің ерекшелігімен анықталады.

Пневматикалық автоматты реттегіштер жарылу және от қауіпті аймақтарда қолданады. Реттеу объектісінен басқару пунктісіне дейінгі арақашықтық 400 м . Гидравликалық реттегіштер жұмыс жасауда сенімділігі жоғары.

Пневматикалық және гидравликалық реттегіштердің кемшілігі:

- арнайы қорек көзіне қажеттілік;

- шектелген әрекет радиусы;

- реттегіш пен байланыс желісінің толық герметикалық жабылуы;

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.