Сығылған стерженьдердің орнықтылығы: Эйлер формуласы, тірек түрлері және кернеулердің әсері


Қазақстан Республикасы Білім және ғылым министрлігі
Шәкәрім университеті
Ақпараттық-коммуникациялық технологиялар факультеті
Автоматика және есептеу техникасы кафедрасы
СӨЖ
Тақырыбы: Орнықтылық
Орындаған: Әбдікәрім Ә
Топ: АУ-601
Тексерген: Секербаева А. Б.
Семей 2018
Жоспар:
Кіріспе
- Аумалы күш. Эйлер фомуласы
- Тірек түрлерінің аумалы күш шамасына әсері
- Кернеулері пропорционалдық шектен ұзын сырықтардың орнықтылығын жоғалтулары туралы түсінік
Қорытынды
Пайдаланылған әдебиеттер
Кіріспе
Конструкция элементтері беріктікке, қатаңдыққа есептелгенде, оған әсер етуші сыртқы күштер мен оның көлденең қималарындағы ішкі күштер өзара орнықты тепе-теңдік күйде деп қарастырылады. Негізінде, кез келген серпімді жүйенің тепе-теңдік күйі орнықты бола бермейді. Мұндай құбылыстар түсінік физика курсынан мәлім:
1. Ойыс беттің ең төменгі нүктесінде жатқан шарды шамалы қозғап еркіне жіберсек, ол өзінің бастапқы орнына қайта оралады (ХІ. 1 а-сурет) . Дененің мұндай күйі орнықты тепе-теңдік күй деп аталады.
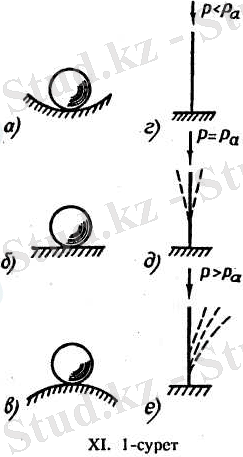
2. Горизонталь жазықтық бетінде жатқан шарды шамалы қозғап еркіне жіберсек, ол бастапқы орнына қайтып келмей, қозғалысын тоқтатады (XI. 1, б-сурет) . Мұндай құбылыс дененің талғаусыз тепе-теңдік күйі деп аталады.
3. Дөңес беттін, ең жоғарғы нүктесіндегі жатқан шарды шамалы қозғап еркіне жіберсек, ол қозғалысын онан әрі шексіз жалғастыра береді (XI. 1, в~сурет) . Мұндай құбылыс дененін орнықсыз тепе-теңдік күйі деп аталады.
Осындай құбылыстарды күш әсер еткен серпімді жүйелерде де байқауға боладьк
Мысалы, шамасы аз бойлық күшпен сығылған стержень иіліп, өзінің түзу сызықты пішінін шамалы өзгерткенімен, орнықты тепе-теңдік күйін жоғалтпайды (ХІ. 1, г-сурет) . Сығушы күш аз шамаға өссе, деформация да аз шамаға өседі. Сыртқы күш әсері жойылса, деформация да жойылып, стержень өзінің бастапқы түзу сызықты орнықты тепе-теңдік күйіне қайтып оралады. Сыртқы күш шамасы кризистік күштен аз ғана артса, сығылған стерженьнің түзу сызықты тепе-теңдік күйі орнықсыз тепе-теңдік күйге айналып, орнықты қисық сызықты тепе-теңдік күйге ауысар еді (ХІ. І д-сурет) . Сызылған стерженьді түзу сызықты тепе-теңдік күйінен ажырататын ең кіші сыртқы күш аумалы күш деп аталады.
1. Аумалы күш. Эйлер фомуласы
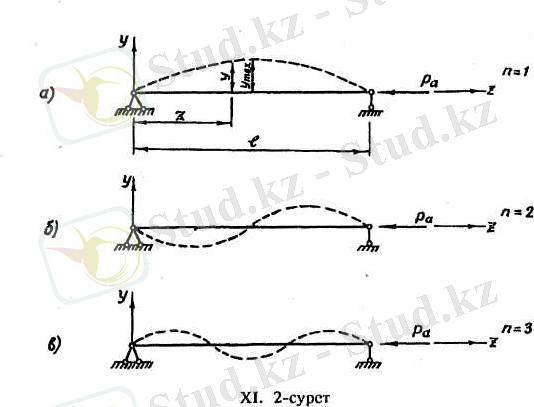
Бойлық ось бойымен сығылған қос топсалы арқалықты қарастырайық. Сығушы күштін шамасы аумалы күшке теңелгенде арқалық орнықтылығын жоғалтпай, шамалы иіліп, талғаусыз тепе-теңдік күйде болады (ХІ. 2, а-сурет) .
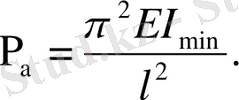 XI. 08
XI. 08
Бұл формуланы 1744 жылы Петербург академиясынын академигі Л. Эйлер ұсынғандықтан, Эйлер формуласы деп атайды.
2. Тірек түрлерінің аумалы күш шамасына әсері
Талғаусыз күйдегі топсалы қос тіректі арқалықтың серпімді сызығы синусоиданың жарты толқынымен сәйкес келеді (XI. 3, а-сурет) . Енді, басқа тіректермен бекітілген аркалықтарды қарастырайық.
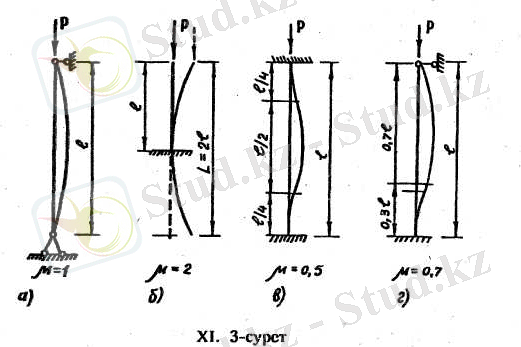
Талғаусыз күйдегі, тіректері әр түрлі стерженьдердің аумалы күштерін анықтайтын Эйлер формулаларын жалпы түрге келтіруге болады:
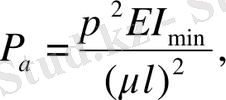 XI. 14
XI. 14
мұндағы l - стерженьнің ұзындығы; μ - тіректердің түрлеріне байланысты қабылданатын, келтірілген ұзындық коэффициенті; μl=l - стерженьнің келтірілген ұзындығы.
Келтірілген ұзындық деп, аумалы күші берілген стерженьнің аумалы күшіне тең топсалы қос тіректі стерженьнің ұзындығын айтады.
3. Кернеулері пропорционалдық шектен ұзын сырықтардың орнықтылығын жоғалтулары туралы түсінік
Талғаусыз тепе-теңдік күйдегі арқалықтың, көлденең қимасындағы тік кернеу келесі формуламен анықталады
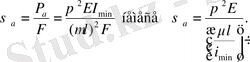
Мұндағы
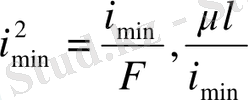 = λ- стержень иілгіштігі деп аталып, стержень өлшемдері мен тірек түрлерінің аумалы шамасына әсерін сипаттайтын өлшем бірліксіз шама. Сонымен, аумалы кернеу
= λ- стержень иілгіштігі деп аталып, стержень өлшемдері мен тірек түрлерінің аумалы шамасына әсерін сипаттайтын өлшем бірліксіз шама. Сонымен, аумалы кернеу
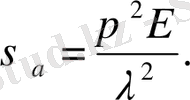 XI. 15
XI. 15
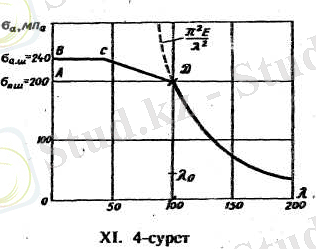
Осы формула бойынша, аа мен X араларындағы тәуелділікті график түрінде көрсетуге болады. Бұл график Эйлер гиперболасы деп аталады. Серпімділік модулі Е = 2*10 5 МПа, пропорционалдық шегі σ пш = 200 МПа болаттан жасалған стерженьнің осындай графигі ХІ. 4-суретте көрсетілген, Графиктен стержень иілгіштігі өскен сайыи аумалы кернеу нолге, ал стержень иілгіштігі кеміген сайын аумалы кернеү шексіздікке ұмтылатындығын байқауға болады. Эйлердің формуласын қорытып шығарғанда серпімді сызықтың дифферендиалдық (ХІ. 04) теңдеуі пайдаланылған. Бұл теңдеу, стержень серпімді деформацияланғанда ғана тиянақты. Сондықтан, Эйлер формуласын сығылған стерженьдердегі тік кернеу пропордионалдық шектен кіші болғанда ғана пайдалануға болады

Бұдан Эйлер формуласының қолдану шарты
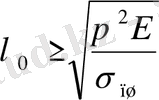 XI. 16
XI. 16
Демек, λ
 λо болганда Эйлер формуласын пайдалануға болмайды. Болаттан жасалған стерженъ үшін
λо болганда Эйлер формуласын пайдалануға болмайды. Болаттан жасалған стерженъ үшін
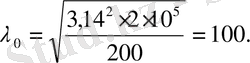
Бұл шаманы, ХІ. 4-суреттегі графиктен де табуға болады. Ол үшін пропорционалдық шегін ордината осіне өлшеп салып, алынған А нүктесі арқылы абсцисса осіне параллелъ түзу жүргізеді. Түзудің Эйлер гиперболасымен қиылысқан нүктесі λо шамасын анықтайды (ХІ. 4-сурет) .
Тік кернеулері пропорционалдық шектерінен үлкен, сығылған стерженьдер үшін аумалы күшті анықтау - күрделі мәселелердің бірі. Көптеген, тәжірибелік зерттеулердің нәтижелеріне сүйеніп Ф. С. Ясинский иілгіштік шамасы кіші (λ<λо) стерженьдердің аумалы кернеулерін анықтауға келесі формуланы ұсынған
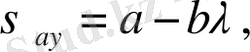 XI. 17
XI. 17
мұндағы а, b - материалдарға байланысты қабылданатын коэффициенттер. Қарастырылған болат үшін а = 3*10 МПа, b= 1, 14 МПa Иілгіштік шамасы
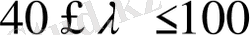 болат стерженьдердің аумалы кернеулері Ясинский формуласымен анықталып, ХІ. 4-суретіндегі DС көлбеу сызығына сәйкес келеді. Иілгіштік шамасы λ < 40 стерженьдер орнықты деп қарастырылып, тек беріктікке есептеледі. Кейбір материалдар үшін а, b коэффициенттері ХІ. І-кестесінде берілген.
болат стерженьдердің аумалы кернеулері Ясинский формуласымен анықталып, ХІ. 4-суретіндегі DС көлбеу сызығына сәйкес келеді. Иілгіштік шамасы λ < 40 стерженьдер орнықты деп қарастырылып, тек беріктікке есептеледі. Кейбір материалдар үшін а, b коэффициенттері ХІ. І-кестесінде берілген.
Сондықтан, сығылған стерженьдер беріктікке есептелумен қатар, міндетті түрде орңықтылыққа да тексеріледі.
Орнықтылық шарты келесі түрде жазылады
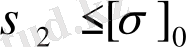
мұндағы
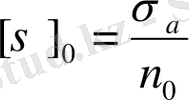 - орнықтылық мүмкіндік кернеуі;
n
0
- орнықтылық қоры коэффициенті.
- орнықтылық мүмкіндік кернеуі;
n
0
- орнықтылық қоры коэффициенті.
Негізгі мүмкіңдік кернеудің коэффициентін
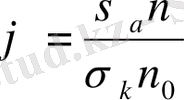 арқылы белгілеп, [σ]
0
, [σ
-
] мүмкіндік кернеулерінің арасындағы байланысты мына түрде жазуға болады
арқылы белгілеп, [σ]
0
, [σ
-
] мүмкіндік кернеулерінің арасындағы байланысты мына түрде жазуға болады
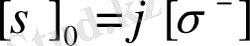 XI. 19
XI. 19
Мұндағы φ - негізгі мүмкіндік кернеуді кемітуші коэффициент.
Негізгі мүмкіндік кернеудің φ коэффициентін стерженьнің кез келген иілгіштігі (λ) үшін есептеп шығаруға болады. Болаттың, шойынның, ағаштың коэффициенттерінің мәндері ХІ. 2-кестеде берілген.
Негізгі мүмкіндік кернеудің φ коэффициентін пайдаланып сығылған стерженьнің орнықтылығын тексеру тәртібі мынадай болады:
1. Өлшемдері мен пішіні белгілі қиманың ең кіші инерция радиусы мен стерженьнің иілгіштігі анықталады
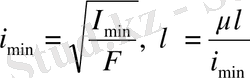
2. Стерженьнің иілгіштігі λ бойынша ХІ. 2-кестеден φ алынып, орнықтылық мүмкіндік кернеуі анықталады [σ ] 0 = φ[σ - ] .
3. Сығылған стерженьнің тік кернеуі орнықтылық мүмкіндік кернеуімен салыстырылып, орнықтылығы тексеріледі
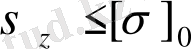 .
.
Сығылған стерженьдер үшін жобалау есебі келесі теңсіздік бойынша шешіледі
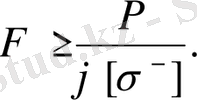
Бұл теңсіздікте Ғ, φ белгісіз. Соңдықтан, олардың бірі беягілі деп есептеліп (мысалы, φ = 0, 5), кима ауданы
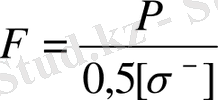 , инерция радиусы ішіп
, инерция радиусы ішіп
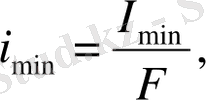
стерженьнің иілгіштігі
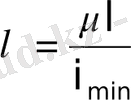 анықталады
анықталады
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz