Колмогоров теңдеулері: формуласы, дәлелдемесі және стационарлық ықтималдықтар


Қазақстан Республикасы Білім және ғылым министрлігі
Шәкәрім университеті
Ақпараттық-коммуникациялық технологиялар факультеті
Автоматика және есептеу техникасы кафедрасы
СӨЖ
Тақырыбы: Колмогоров формуласы мен түсіндірмесі
Орындаған: Әбдікәрім Ә
Топ: АУ-601
Тексерген: Секербаева А. Б.
Семей 2018
Жоспар:
Кіріспе
- Жүйе жай-күйінің соңғы ықтималдығы
- Мысал
Қорытынды
Пайдаланылған әдебиеттер
Кіріспе
Жүйеде соңғы сандар саны болсын және онда кездесетін кездейсоқ процесс әрқайсысында жүйені табудың ықтималдылығымен сипатталады.
Үздіксіз уақыт және соңғы сандар саны бар Марков жүйесі жағдайында олардың ықтималдығын Колмогоров дифференциалдық теңдеулер жүйесін шешу арқылы табуға болады:
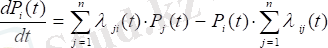 (1)
(1)
Бұл құндылық күйден-күйге көшу ықтималдығының ағымы деп аталады.
Колмогоров теңдеулері жүйенің белгілі бір күй графигіне негізделіп, келесі ережені қолданады: әр күйдің ықтималдық туындысы басқа күйлерден осы ықтимал ағымдарға дейінгі барлық ықтималдық ағындарының сомасына тең, бұл осы күйлерден басқаларға баратын барлық ықтималдық ағындарының сомасы.
Колмогоров теңдеулер жүйесін шешу кезінде бастапқы ықтималдығын бөлуді көрсету керек. Ерекше қарапайым жүйелерді қоспағанда, шешім тек сандық әдістермен ғана алынуы мүмкін.
1. Жүйе жай-күйінің соңғы ықтималдығы
Егер жүйеде орын алған процесс жеткілікті ұзағырақ болса, онда ықтималдықтың шектеулі мінез-құлқы туралы айтуға болады. Кейбір жағдайларда, соңғы (шекті) күйдің ықтималдығы бар:
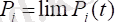 (2)
(2)
жүйе бастапқы кезде болған күйден тәуелсіз. Жүйеде күйден-күйге өтетін шектік стационарлық режим құрылады деп айтылады, бірақ жағдайлардың ықтималдығы уақытпен өзгермейді. Соңғы жағдайлары бар жүйе эргодикалық деп аталады, ал тиісті кездейсоқ процесс эргодикалық деп аталады.
Жүйенің соңғы ықтималдығы Колмогоров дифференциалдық теңдеулерден алынады, егер туындылар нөлге тең болса, Колмогоров теңдеулерінің оң жақ бөліктеріндегі ықтималдық функциялары белгісіз түпкілікті ықтималдықтармен алмастырылған сызықты алгебралық теңдеулер жүйесін шешу арқылы алынады.
Осылайша, күйлермен жүйе үшін белгісіздермен сызықты біртекті алгебралық теңдеулер жүйесі алынады, ол тұрақты факторға дейін жетеді. Олардың дәл мәндерін табу үшін қалыпты жағдай теңдеулерге қосылады, ол арқылы кез-келген ықтималдылықты басқалар арқылы білдіруге және теңдеулердің бірін алып тастауға болады.
2. Мысал
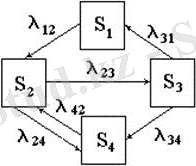
1-сурет
Көрсетілгендей, шағын уақыт аралығы үшін (Dt << max [1 / lij] ) мемлекет i-дан j j p ij (Dt) -қа көшу ықтималдығы lj × Dt (i ¹ j) . Біз p1 (t) ықтималдығын табу міндетін қойдық, яғни S кезіндегі S1 күйінде жүйені табу ықтималдығы. Біз Dt-нің шағын артуын береміз және жүйе T + Dt кезінде S1 күйінде болатындығын табамыз. Бұл оқиға екі жағдайда болуы мүмкін:
- t уақытта жүйе S1 күйінде болды және Dt кезінде жүйенің күйі өзгермеді;
- t уақытта жүйе S3 күйінде болды және Dt кезінде S3 күйінен S1 күйіне ауысты.
Бірінші нұсқа ықтималдығы p1 (t) × (1-112Dt), екінші ықтималдығы p3 (t) × l31Dt. Ықтималдылықты қосу ережесін қолдану, біз аламыз
p1 (t + Dt) = p1 (t) × (1-112Dt) + p3 (t) × l31Dt.
Осыдан,
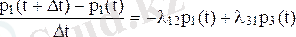
Dt®0 шегіне дейін өтетін дифференциалдық теңдеуді алуға мүмкіндік беретін p1 (t) ықтималдығы:
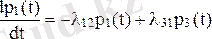
Сол әдісті пайдалана отырып, біз p2 (t) ықтималдық үшін дифференциалдық теңдеуді табамыз. P2 (t + Dt) ықтималдығын анықтаймыз, яғни жүйе T + Dt кезінде S2 күйінде болатындығы ықтималдығы. Бұл оқиға келесі жолдармен кездеседі (1-сурет) :
- T уақытында жүйе S2 күйінде болды және Dt кезінде жүйенің күйі өзгерген жоқ.
p2 (t) × (1-l23Dt-l24 Dt) .
- T уақытында жүйе S1 күйінде болды және Dt уақыт S1 күйінен S2 күйіне ауысты. Бұл оқиғаның ықтималдығы p1 (t) × l12 × Dt.
- T уақытында жүйе S4 күйінде болды және Dt уақыт S4 күйінен S2 жайына ауысты. Бұл оқиғаның ықтималдығы p4 (t) × l42 × Dt.
Өйткені Dt (Dt << max [1 / lij] ) екі немесе одан да көп ауысу ықтималдығы аз, қажетті ықтималдық
p2 (t + Dt) = p2 (t) × (1-l23 Dt-l24 Dt) + p1 (t) × l12Dt + p4 (t) × l42Dt.
Өзгерістер жасай отырып, Dt®0 шегіне жеткенде, біз р2 (t) ықтималдығын қанағаттандыратын дифференциалдық теңдеуді аламыз:
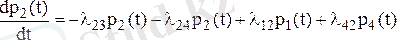
Осындай пікірмен біз дифференциалдық теңдеулер жүйесін (Колмогоров теңдеуі) аламыз:
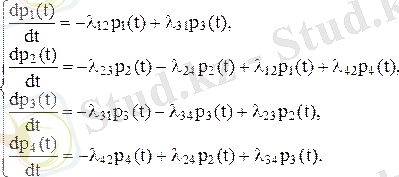
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz