Шектік цикл

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 7 бет
Таңдаулыға:

Қазақстан Республикасы Білім және ғылым министрлігі

Шәкәрім университеті

Ақпараттық-коммуникациялық технологиялар факультеті

Автоматика және есептеу техникасы кафедрасы

СӨЖ

Пән: Бейсызықты автоматты реттеудің жүйелері

Тақырыбы: Сызықсыз жүйенің фазалық бейнеленуі

Орындаған: Әбдікәрім Ә. Қ.

Топ: АУ-601

Тексерген: Секербаева А. Б.

Семей 2019

Жоспар:

Кіріспе

Шектік цикл
Бейсызықты жүйелердің фазалық траекториясының типтік жағдайлары
Сезімталсыз аймағы бар бейсызықты жүйелер

Қорытынды

Пайдаланылған әдебиеттер

Кіріспе

Кіріс және шығыс сигналдарының сипатталуы:

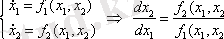
Анықталмағандығы:

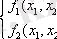
Бейсызықты жүйелердің фазалық портреттерінің сызықты жүйелерден принципті айырмашылықтары оның қасиеттерінен туындайды. Егер сызықтық жүйе тұрақты болса, онда фазалық жазықтықтың кез келген нүктесінен фазалық траекториялар координаталардың басталуына ұмтылатын болады, егер сызықтық жүйе тұрақсыз болса, яғни оның тепе-теңдік жағдайы тұрақсыз болса, онда кез келген бастапқы жағдайларда фазалық траекториялар координаталардың басталуына ұмтылатын болады. Бейсызықты жүйеде ерекше нүктенің сипаты фазалық траекториялардың тек координаталардың басына жақын, яғни жүйенің тепе-теңдік күйінен аз ауытқулар кезінде мінез-құлқын анықтайды. Егер сызықсыз жүйенің тепе-теңдігінің жағдайы тұрақсыз және процесс шығындалса, онда ол шектеусіз шығындалмайды: жүйедегі тербелістердің амплитудасы белгілі бір шекке дейін өсуі және одан әрі тұрақты қалуы мүмкін. Координаттардың басында тұрған ерекше нүктеден басқа фазалық портрет ерекше траекторияны - шекті циклді қамтиды.

Сызықты жүйелермен салыстырғанда бейсызықты жүйелерде ерекше сызықтар болады. Ал ерекше нүктелер: ортасы, түйіні, фокусы, ертоқым және т. б.

Ерекше сызықтар: орнықты шектік цик (фазалық траектория тұйықталған), орнықсыз шектік цикл, орнықты күй сызығы, сепаратрисс сызығы (фазалық траекториясы әртүрлі облыстарды бөлетін сызық) .

Ерекше нүктелерді анықтау үшін жүйе теңдеуі оның маңынды сызықтандырылады, содан кейін сызықталған жүйенің сипаттамалық теңдеуінің түбірлері анықталады:

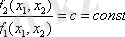
1. Шектік цикл

Шекті цикл - фазалық траекториялар координаттардың басынан бұрыла отырып, жақындап келе жатқан тепе-теңдік жағдайына жақын оқшауланған тұйық траектория. Оған шекті циклдің сыртында жүрген траекториялар да бар. Шекті циклдер жүйедегі автотербелістерге сәйкес келеді және тұрақты немесе тұрақсыз болуы мүмкін. Тұрақты шекті цикл жағдайында фазалық траекториялар сыртынан және ішінен шекті циклге бұралады. Мұндай жүйеде нақты жағдайларда автотербеліс режим бақыланады. Егер фазалық траекториялар екі жағынан шектік циклден алыстатылса, онда ол тұрақсыз деп аталады және тұрақсыз автотербелістерге сәйкес келеді. Мұндай жүйеде байқалуы мүмкін нақты процестер бастапқы жағдайларға байланысты.

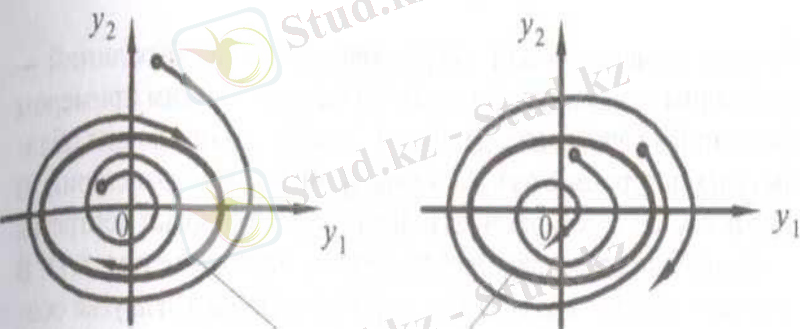
Безымянный.png

Автотербелістері бар бейсызықты жүйелердің фазалық портреттерінің мысалдары

Егер бейнелейтін нүкте шекті цикл ішінде болса, онда ол координаталардың басына фазалық траекториямен қозғалады, яғни жүйе тепе-теңдік жағдайына жақындай отырып, өзін тұрақты ретінде жүргізеді. Егер бастапқы сәтте бейнелейтін нүкте шекті циклдің сыртында болса, онда жүйеде тербеліс амплитудасы шексіз және қарастырылатын жүйе "кіші" және "үлкен"тұрақты болады. Тұрақсыз автотербелістік режимдер кездейсоқ ауытқулар әсеріне ұшыраған нақты жүйелерде байқалмайды. Жүйеде бір-бірінен амплитудамен және кезеңмен ерекшеленетін бірнеше мүмкін болатын автотербелістік режимдерге сәйкес келетін бір емес, бірнеше шекті цикл болуы мүмкін.

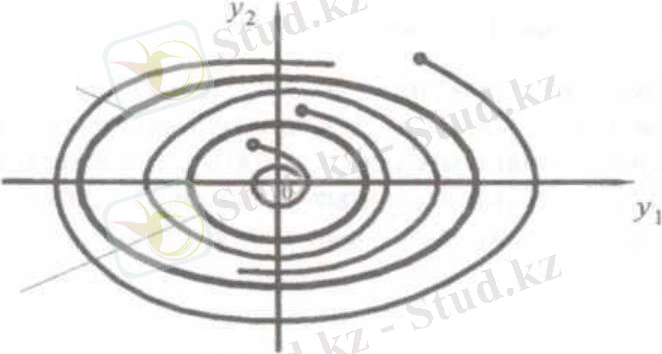
Безымянный2.png

Екі шекті циклі бар бейсызықты жүйенің фазалық портреті

2. Бейсызықты жүйелердің фазалық траекториясының типтік жағдайлары

1. Орнықты шектік цикл (автотербелістер)

Оның фазалық траекториясы шектік циклге ұмтылады, цикл орнықты болады.

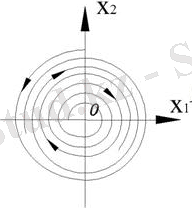
1-сурет. Фазалық портреті және өтпелі үрдісі

Бұл жағдайда жүйе кіші аумақта орнықсыз ((0, 0) нүктесінде - орнықсыз фокус), бірақ үлкен аумақта - орнықты.

2. Орнықсыз шектік цикл

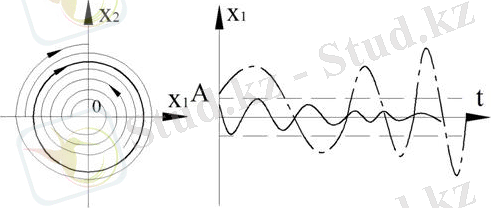
2-сурет. Фазалық портреті және өтпелі үрдісі

Бұл жағдайда кіші аумақта жүйе орнықты, үлкен аумақта - орнықсыз.

3. Бірнеше шектік циклдер

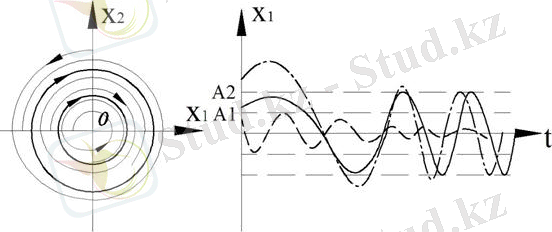
3-сурет. Фазалық портреті және өтпелі үрдісі

Бұл кезде сыртқы шектік цикл орнықты, ішкісі - орнықсыз.

4. Сепаратрисса

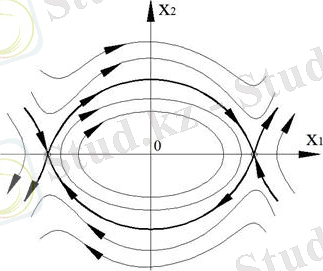
4-сурет. «Сепаратрисса» типті ерекше нүкте

Мұндағы ерекше нүктелер: ортасы және екі ертоқым.

Ерекше нүктелердің жіктелуі

Автономды дифференциалдық теңдеулер жүйесін қарастырайық:

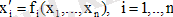(1)

(1) үшін айнымалылар кеңістігі 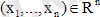фазалық кеңістік болып табылады. Егер n=2, онда фазалық кеңістік фазалық жазықтық болып табылады. Мұндағы t нүктесі 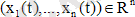- фазалық нүкте деп аталады. Ал 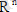қисық сызықтар фазалық траекториялар. Фазалық траекторияның бағыты деп t артатын бағыттағы фазалық нүктенің қозғалыс бағытын 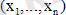айтады. Ал фазалық жазықтықта фазалық траекториялар салатын сурет фазалық портрет деп аталады.

(1) жүйеде, 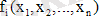оң жақтары үздіксіз және үздіксіз жеке туындылар болса 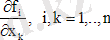, онда фазалық траекторияның үш түрі мүмкін: нүкте, тұйықталған, тұйықталмаған қисық. Нүктелер жүйенің тепе-теңдік күйіне сәйкес келеді. Тұйықталған қисық периодты шешімді, ал тұйықталмаған - периодты емес шешімді білдіреді.

n=2 кезінде (1) жүйесі тұрақты коэффициенттері бар біртекті дифференциалдық теңдеулер жүйесі болсын:

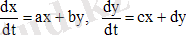(2)

(2) жүйені сапалы зерттеудің негізгі мақсаты - оның фазалық кеңістігінің сапалы суретін алу. Жүйенің фазалық траекториясының жүрісі сипаттамалық теңдеудің түбірлерін 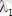және 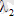анықтайды:

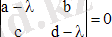. (3)

Бұл түбірлер нақты немесе кешенді шамалар бола алады. Кестеде ерекше нүктелердің фазалық траекторияларының жіктелуі көрсетілген.

Дикритикалық түйін

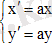
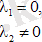
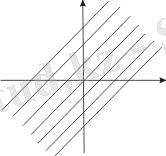
Бұл жағдайда жүйе түрі

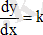
Траекториясы - түзу

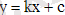
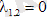
Барлық фазалық жазықтық

3. Сезімталсыз аймағы бар бейсызықты жүйелер

Сезімталсыз аймағы және құрғақ үйкеліс аймағы бар элементтері бар сызықсыз жүйелердің ерекшелігі - белгіленген жағдайға сәйкес келетін стационарлық режимдер аймағының болуы.

Фазалық жазықтықта бұл ерекше нүктені тарту арқылы көрінеді, мысалы, түйін ерекше сызыққа.

Сезімталсыз аймағы бар сызықсыз жүйенің фазалық портреті екінші ретті сызықты жүйелер үшін фазалық портреттерді тұрғызу фазалық траекториялардың теңдеулері бойынша тікелей орындалуы мүмкін.

Бейсызықты жүйелер үшін міндет қиындайды, өйткені. көп жағдайда аналитикалық түрде фазалық траекториялар үшін теңдеуді алу мүмкін емес.

Бейсызықты жүйелердің фазалық портреттерін құру үшін жуықталған әдістерді қолданады:

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.