Шеннон теоремалары: арна сыйымдылығы және кодтау негіздері


Қазақстан Республикасы Білім және ғылым министрлігі
Шәкәрім университеті
Ақпараттық-коммуникациялық технологиялар факультеті
Автоматика және есептеу техникасы кафедрасы
СӨЖ
Тақырыбы: Шеннон теоремалары
Орындаған: Әбдікәрім Ә
Топ: АУ-601
Тексерген: Секербаева А. Б.
Семей 2018
Жоспар:
Кіріспе
- Бірінші теорема
- Шеннон-Хартли немесе Шеннонның екінші теоремасы
- Шеннонның дискретті бөгеті бар арна үшін теоремасы
- Шеннонның дискретті бөгеусіз арна үшін теоремасы
- Қорытынды
Пайдаланылған әдебиеттер
Кіріспе
Клод Элвуд Шеннон ( ағыл. Claude Elwood Shannon; 30 сәуір, 1916, Петоски, Мичиган, АҚШ - 24 ақпан, 2001, Медфорд, Массачусетс, АҚШ) - американдық инженер, криптоаналитик және математик. Ол «ақпараттық ғасырдың әкесі» деп саналады.
Ол заманауи жоғары технологиялық коммуникация жүйелерінде қолданылатын ақпараттық теорияның негізін қалаушы. Қазіргі кезде қазіргі заманғы коммуникациялық технологиялар үшін негіз болып табылатын негізгі ұғымдар, идеялар және олардың математикалық формулаларын енгізген. 1948 жылы ол «бит» деген сөзді ең кішкентай бірлікті белгілеу үшін қолданды («Математикалық байланыс теориясы») . Сонымен қатар, энтропия түсінігі Шеннон теориясының маңызды ерекшелігі болды. Ол ендірілген бойымыздағы хабар жіберілген хабарламада ақпараттық белгісіздікке тең екендігін көрсетті. Шеннонның «Байланыс жүйесінің математикалық теориясы» және «Құпия жүйелердегі байланыс теориясы» мақалалары ақпараттық теория мен криптографияға негіз болып табылады. Клод Шеннон криптографияны ғылыми тұрғыдан жақындастырғандардың бірі болды, ол өзінің теориялық негіздерін тұжырымдайтын және көптеген негізгі ұғымдарды ұсынды. Шеннон ықтималдық схемалар теориясы, ойын теориялары, автомат теориялары және басқару жүйесі теориясы - кибернетика тұжырымдамасының бөлігі болып табылатын ғылым салалары үшін маңызды үлес қосты.
1. Бірінші теорема
Шеннонның интерференция болмаған кезде негізгі кодтау теоремасы деп аталатын ақпаратты беру туралы алғашқы теоремасы келесідей тұжырымдалған:
Жеткізу кедергісі болмаған жағдайда, кодталған алфавиттің бір таңбасына арналған кодтық таңбалардың орташа саны бастапқы ақпаратты және орташа алфавиттердің белгісіне орташа ақпараттың арақатынасына жақын болады.
Қайта көбейту кодының тұжырымдамасын қолдану арқылы сіз теореманы қысқаша тұжырымдай аласыз:
Жеткізу кедергісі болмаған жағдайда, кодты босату нөлге жақын болады, әрдайым хабарды кодтау нұсқасы болады.
Бұл мәлімдемелер теоремалар болып табылады және сондықтан да дәлелдеуге болады, бірақ дәлелдерді жоққа шығарамыз. Теоремент оңтайлы кодтаудың іргелі мүмкіндігін ашады. Дегенмен, теореманың өзі мұндай кодтауды іс жүзінде қалай жүзеге асыруға болатынын түсінбеу керек - бұл үшін кейіннен талқылаудың мәні болатын кейбір қосымша ойларды тарту керек.
Сонымен қатар, біз негізінен өзімізді M = 2 , яғни, байланыс желісіндегі кодтарды ұсыну үшін практикалық тұрғыдан алғанда, сигналдың екі түрін ғана қолдануға болады (мысалы, сымның кернеуінің болуы (оны импульстік деп атаймыз) немесе оның жоқтығы (үзіліс), бұрылысты картада немесе магниттелген аймақта тесік бар немесе болмауы дискетте) ; бұл кодтау екілік деп аталады. Бинарлық алфавиттің кейіпкерлері әдетте «0» және «1» деп белгіленеді, бірақ олар сандар емес, әріптер ретінде қабылданады. Екілік кодтардың қолайлылығы, бірдей ұзақтықпен және ықтималдықпен, әрбір қарапайым сигнал (0 немесе 1) 1 бит ақпаратқа ие ( log2M = 1 ) ; онда Шеннон теоремасы (1)
I
1
(A)
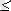 K
(2)
K
(2)
Шеннонның алғашқы теоремасы мынадай түсіндірмені алады:
Жеткізу кедергісі болмаған жағдайда, екілік кодтың орташа ұзындығы негізгі алфавиттік таңбаға тән орташа ақпаратқа жақын болуы мүмкін.
Бинарлық кодтау үшін формуланы (2) пайдалану:
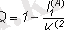
Екілік кодтауда берілген ақпараттардың мөлшерін анықтау импульстардың (олардың) саны мен үзілістердің (нөлдер) қарапайым санына дейін азаяды. Бұл жағдайда сигнал ағынының жекелеген кодтарын (импульстердің және үзілістердің реті) алу проблемасы туындайды. Қабылдаушы құрылғы сигналдардың қарқындылығы мен ұзақтығын белгілейді. Бастапқы сигналдар (0 және 1) бірдей немесе әр түрлі ұзақтықтарға ие болуы мүмкін. Бастапқы алфавиттің белгісіне қойылған кодтағы олардың коды (код тізбегінің ұзындығы) да бірдей болуы мүмкін (бұл жағдайда код бірыңғай деп аталады) немесе әр түрлі (біркелкі емес код) болуы мүмкін. Ақыр соңында кодтар бастапқы алфавитінің (әліпбилік кодтау) әрбір таңбасына немесе олардың комбинациясына (блоктарды, сөздерді кодтау) арналған болуы мүмкін. Нәтижесінде, кодтау кезінде (алфавиттік және ауызша) келесі комбинациялар мүмкін:
Біркелкі емес кодтау немесе әртүрлі ұзақтықтағы сигналдар (жағдай (2), (3) және (4) ) пайдаланылған жағдайда, олардың арасындағы бір таңбаның кодын бөлек ажырату үшін арнайы сигнал - уақытша бөлгіш (белгі белгісі) немесе осы кодтарды қолдануы керек бірегей болу үшін, яғни басқа кодтардың бөліктерімен сәйкес келмейді. Сол ұзақтық сигналдарының біркелкі кодтауымен (жағдай (1) ), бір кодты басқа бірінен бөлу барлық кодтар үшін бірдей (немесе сақтау кезінде бит саны бірдей) жалпы ұзақтыққа сәйкес жасалғандықтан, арнайы сепаратор қажет емес.
Бинарлы қарапайым импульстың ұзақтығы (
 ) 1 бит ақпаратты беру үшін қанша уақыт қажет екенін көрсетеді. Әрине, бастапқы алфавит бойынша орташа есеппен ақпарат беру уақытын
) 1 бит ақпаратты беру үшін қанша уақыт қажет екенін көрсетеді. Әрине, бастапқы алфавит бойынша орташа есеппен ақпарат беру уақытын
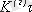 талап етеді. Осылайша, кодтаудың оңтайландыру мәселесі басқа жағдайларда тұжырымдалуы мүмкін: мұндай кодтау жүйесін құру, осы хабарламаның беру кезінде кодтардың жалпы ұзақтығы (немесе сақтау кезінде кодтардың жалпы саны) қысқа болуы мүмкін.
талап етеді. Осылайша, кодтаудың оңтайландыру мәселесі басқа жағдайларда тұжырымдалуы мүмкін: мұндай кодтау жүйесін құру, осы хабарламаның беру кезінде кодтардың жалпы ұзақтығы (немесе сақтау кезінде кодтардың жалпы саны) қысқа болуы мүмкін.
2. Шеннон-Хартли немесе Шеннонның екінші теоремасы
Клод Шэннон ақпараттың көлемін айқындаған кезде, шулы коммуникациялық арналардың өткізу қабілеті туралы керемет теореманы дәлелдеді. Бұл теория 1957-1961 жж. өз жұмыстарында жарияланды және қазір оның атын атайды. Шын мәнінде, бұл бір теорема емес, әртүрлі жағдайларға арналған ондаған теоремалар. Шеннонның теоремасының мәні неде? Әр шулы байланыс арнасы Шеннон шегі деп аталатын ең жоғары (ең жоғары) ақпарат беру жылдамдығы (өткізу қабілеті) арқылы сипатталады. Берілген шектеуден жоғары беру жылдамдығында жіберілген ақпараттың қателері сөзсіз. Бірақ төменнен осы шектеуді қалағаныңыздай жақындай аласыз, бұл ақпараттың тиісті кодтауы сіз кез келген арна шуында еркін қателік ықтималдығын қамтамасыз етеді.
Шеннон-Хартли теоремасы барлық ықтимал көп қабатты және көпфазалы шифрлау әдістерін ескере отырып, С-арнасының сыйымдылығын, ол деректерді беру жылдамдығының теориялық жоғарғы шегін білдіретін, бұл ретте А сигналының белгілі бір қуаты S арқылы аналогтық байланыс арнасы арқылы берілуі мүмкін. :
C = F × log2 (1 + S/N) ; (3)
C/F ≈ 1. 44 × S/N, (4)
мұндағы
C - арна сыйымдылығы (өткізу қабілеті), бит / с;
F - өткізу жолағының ені, Гц;
S - өтпелі жолдың үстіндегі сигналдың жалпы қуаты, W немесе B2;
N - өтпелі жолақтың үстіндегі шудың толық күші, W немесе B2;
S/N - қуат коэффициенті ретінде көрсетілген RMS сигналының қуатын беру жүйесінің Гаусс шуының RMS қуатына қатынасы.
Ақпарат беру жүйесінің беру қабілеті трансмиссиялық жиілік диапазонының еніне тікелей пропорционалды. Мысалы, стандартты телефон арна үшін өткізу жолағы F = 3 кГц, N / S = 30 дБ, сондықтан жалпыға ортақ пайдаланылатын телефон желісінің теориялық лимиті шамамен 30 кбит / с. Телефонның бұрылыс жұптары үшін шамамен 15 дБ / километрді жоғалту, керуенге байланысты қосымша шектеулер туындайды.
Дискретті (цифрлық) нысанда берілетін F диапазонымен аналогтық сигнал қарастырсақ, онда Котельников теоремасына сәйкес, сынама жиілігі 2F (8 кГц) тең немесе артық болуы керек. Үлкен іріктеу жиіліктерін қолданғанда, жоғары гармоника ойнатылғанда алынуы мүмкін, бірақ олар белгілі бір өткізу қабілеттілігіне кедергі келтіреді. N дискретті түрлендіру деңгейлерінде максималды деректер ағымы F = 4 кГц / с және N = 256 квантизация деңгейлерінде болатын 2F × log2 (N) бит / с болады. Жеткізу жиілігі 8 есе кеңірек және 64 кбит / с жылдамдықта болады. F = 4 кГц, тіпті шу болмаған кезде, 8 кбит / с-тан астам беру жылдамдығы алынбайды (сағатына бір бит болса) .
Дәл осылай аналогтық аудио сигналда F = 22. 05 кГц жиіліктер диапазоны және оның жоғары сапалы цифрлық берілімі үшін бинарлық кодта 16 бит бар, F = 2. 03 Мбит / с жиілік диапазоны қажет. Қалыпты теледидар кескіні F = 4 МГц жиілік ауқымында аналогтық сигнал, ал F = 32 Мбит / с сигналының 256 квантизация деңгейінде беріледі. Жоғары ажыратымдылықтағы цифрлық теледидарда (HDTV) өткізудің өткізу қабілеті 504, 3 Мбит / с.
Шэннон негізінен Найквист идеясын дамытты. Егер сигналдың екілік көрінісі пайдаланылса, онда Котельников - Найквист сынамалық үлестіру теоремасы бойынша [1924], егер араласусыз арнадағы деректерді беру жылдамдығы ең жоғары болады:
I = 2F × log2V [бит / с], (5)
мұндағы
F - арнаның өткізу жолағын Гц;
V - сандық конвертердің дискретті сигнал деңгейінің саны.
Таңдау теоремасының мәні сигналдың өткізу қабілеттілігі F болғанда, қабылдау жиілігі бастапқы сигналдың пішінін дұрыс қалпына келтіру үшін 2F-ден артық болуы керек. Осы себепті, <a href = «/ index. php / communication / 81-chrk"> F = 3 кГц өткізу қабілеті бар стандартты телефон арнасы, кедергі болмаған жағдайда және V = 2 арқылы 6 кбит / с-тан жоғары жылдамдықты беру мүмкін емес. Шеннон теоремасы қайшы емес. Шынында да, кедергі болмаған жағдайда, V мәні жоғары болмайды! Бұл сигналдың ең үлкен амплитудасы киловольтқа жетуі мүмкін дегенді білдірмейді. Келісіңіз, мұндай перспективалар телефон абоненттеріне жағымды әсер қалдырады. Бірақ кедергі болмаған жағдайда, бір вольттағы сигнал деңгейінің кез-келген санын елестету мүмкін. Шаннонның теоремасы шу деңгейінің берілген ең жоғары сигнал амплитудасының V шамасының шектеуін қалай анықтайтынын түсіндіреді.
Шеннон теоремасынан нөлдік кедергі деңгейінен төмен жылдамдықтағы каналдың өткізу қабілетін төмендетуге болады. Екінші жағынан, егер байланыс каналының өткізу жолағының ені H көзінің бойымен антропиядан үлкен болса, онда хабарды кідірместен орта есеппен жүргізілетін етіп кодтау мүмкін болады. Шеннон теоремасының мәні, егер байланыс арнасының өткізу қабілеті жеткілікті үлкен болса, уақытты кешіктіру мүмкін болса да, олар қандай да бір жолмен «еріп кетеді».
Шеннонның шулы арнаға арналған теоремасы арнаның сыйымдылығына ерікті түрде жылдамдықпен сенімді ақпаратты беруді қамтамасыз ететін нақты кодтау әдісін көрсетпейді, бірақ мұндай әдісті іргелі тұрғысынан ғана көрсетеді. Бұдан басқа, кодтауды кешіктіріп жіберілген хабармен қоса жүреді. Сондықтан, тамаша кодтау техникалық мүмкін болмайды. Дегенмен, қате ықтималдығы үшін формуладан өте маңызды практикалық тұжырымдама бар: хабарлардың сенімді болуы неғұрлым сенімді болса, арна ретіндегі кодтау ұзағырақырақ және каналдың сыйымдылығы азырақ қолданылады. каналдың өткізу қабілеттілігі көбірек көзден (Ck> Vu) жұмыс істеуден асып түседі.
3. Шеннонның дискретті бөгеті бар арна үшін теоремасы
Бөгеу - пайдалы сигналға қосылып және оның қабылдануына кедергі жасайтын кез-келген әрекет. Бөгеулер пайда болуына да, сондай-ақ физикалық қасеттеріне де байланысты әр түрлі.
Өткізгіш байланыс арналарында бөгеулердің негізі болып импульстік шуылдар мен байланыстың үзілісі болып табылады. Импульсті бөгеулердің пайда болуы көбінесе автоматты коммутация және қиылысты апарумен байланысты. Байланыстың үзілу құбылысы кезінде желідегі сигнал кенеттен өшеді немесе мүлдем жойылады.
Тәжірибеде кез келген жиілік диапазонында аппаратураның күшейткіш құрылғыларындағы, кедергілерде және тағы басқа аппарат элементтерінде заряд тасымалдаушылардың бейберекет қозғалуынан болатын ішкі шуылдары кездеседі. Бұл бөгеудің түрі әсіресе, ультрақысқа толқындар диапазонына әсер етеді. Бұл диапазонда сонымен қоса, күнде, жұлдыздарда және басқа да ғарыштық объектілерде болатын электромагниттік процесстермен байланысқан ғарыштық бөгеулері бар.
Бөгеулердің классификациясын келесі белгілер бойынша құруға болады:
- пайда болуына байланысты (пайда болған орны) ;
- физикалық қасиеттеріне байланысты;
- сигналға әсер етуіне байланысты.
Бөгеулердің пайда болуына ең алдымен аппаратураның күшейткіш құрылғыларындағы, кедергілерде және тағы басқа аппарат элементтерінде заряд тасымалдаушылардың бейберекет қозғалуынан болатын ішкі шуылдары (жылулық шуылдар) әсер етеді. Кез келген өткізгіштегі зарядтардың кездейсоқ жылулық қозғалысы потенциалдар айырмасына әкеледі. Кернеудің орта мәні нөлге тең, ал айнымалы құраушысы шуыл ретінде болады. Жылулық шуылдардағы кернеудің эффективті квадраты белгілі Найквист формуласымен анықталады.
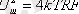 . (6)
. (6)
Мұндағы Т- абсолютті температура, R кедергісі ; F - жилік жолағы; k =1, 37*10 (-23) Вт. сек/град-Больцман тұрақтысы.
Пайда болуына байланысты бөгеулер келесіше бөлінеді:
- байланыс арнасынан тыс бөгде таратқыштан болатын бөгеулер;
- атмосфералық бөгеулер (найзағай кезіндегі разрядтар, полярлық жарқырау, және т. б. ), атмосферадағы электрлік процестермен байланысты;
- индустриалды бөгеулер, электрқондырғыларда пайда болатын бөгеулер (электрокөлік, электрлік қозғалтқыштар, медициналық қондырғылар және басқалар. ) ;
- бөгде арналар мен станциялардан болатын бөгеулер;
- ғарыштық бөгеулер, күн бетіндегі, жұлдыздардағы, ғаламшардағы және басқа жерден тыс объектілердегі электромагнитті үрдістерге байланысты.
Физикалық қасиеттерге байланысты бөгеулер:
- флуктуациялық бөгеулер;
- шоғырланған бөгеулер.
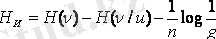 .
.
Ақпаратты жіберу жылдамдығы:
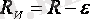 , мұндағы
, мұндағы
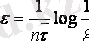 . (7)
. (7)
Арна бойынша ақпаратты жеткізудегі максималды жылдамдығы maxR=C
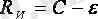 . (8)
. (8)
Бір мезетте құру мүмкіндігі декодтық қателіктің аз ықтималдығында Р ОД және ε аз өлшемдегі пайдасы Шеннон теоремасының шындығын дәлелдейді.
Жоғары мөлшердегі кедергісі бар дискретті арналарда ақпаратты жіберу теориясындағы негізгі мәндері бар теореманы Шеннон дәлелдеді. Бұл теорема келесі жолдармен қалыптасуы мүмкін.
Егер таратқыштың өнімділігі
R
и
 C-ε
, бұл жерде
ε-
өте аз шамада болғандықтан, барлық мәліметтерді аз мөлшердегі қателіктермен кодтау әдісі бар. Егер
Rи>C
болса, бұлай жіберу мүмкін емес.
Әрбір топқа типтік ауысу мөлшері:
C-ε
, бұл жерде
ε-
өте аз шамада болғандықтан, барлық мәліметтерді аз мөлшердегі қателіктермен кодтау әдісі бар. Егер
Rи>C
болса, бұлай жіберу мүмкін емес.
Әрбір топқа типтік ауысу мөлшері:
М Г =2 nH(v/u) . (9)
Жалпы жағдайда ауысулар айқастандырылады, яғни бір ғана тізбек V j .
Бірнеше тізбектің U бір тізбегі жіберілу нәтижесінде пайда болуы мүмкін.
Декодтаудағы қателік ықтималдығы:
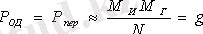 .
(10)
.
(10)
М И - ақпаратты тасымалдауға арналған тізбек саны;
Р пер - тасымалдаулардың айқастану ықтималдығы.
Бұл ықтималдық шамасы өте жақын болып табылады, бірақ Р ОД пен М И арасындағы тәуелділікті сипаттауға дұрыс бағыт береді.
Егер таратушынын энтропиясы Н И тең болса, онда:
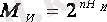 . (11)
. (11)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz