Температураның жылуға тәуелділігі

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 66 бет
Таңдаулыға:

Мазмұны

Белгілеулер мен қысқартулар . . .

Белгілеулер мен қысқартулар . . .: Кіріспе . . .

3: 4

Белгілеулер мен қысқартулар . . .: 1 Термодинамиканың негізгі ұғымдары . . .

3: 5

Белгілеулер мен қысқартулар . . .: 1. 1 Идеал газдардың молекула-кинетикалық теориясы . . .

3: 5

Белгілеулер мен қысқартулар . . .: 1. 2 Термодинамика заңдары . . .

3: 9

Белгілеулер мен қысқартулар . . .: 1. 3. Нақты газдар және фазалық өзгерістер . . .

3: 17

Белгілеулер мен қысқартулар . . .: 2 Жылудың негізгі қасиеттерін тәжірибе жүзінде қарастыру . . .

3: 21

Белгілеулер мен қысқартулар . . .: 2. 1 Металдың жылусыйымдылығының ерекшелігі . . .

3: 21

Белгілеулер мен қысқартулар . . .: 2. 2 Температураның жылуға тәуелділігі . . .

3: 27

Белгілеулер мен қысқартулар . . .: 2. 3 Жылудың булануы . . .

3: 32

Белгілеулер мен қысқартулар . . .: 2. 4 Термиялық жылу . . .

3: 40

Белгілеулер мен қысқартулар . . .: 3. Температураның қасиеттерін сипаттау . . .

3: 46

Белгілеулер мен қысқартулар . . .: 3. 1 Фазалық ауысу . . .

3: 46

Белгілеулер мен қысқартулар . . .: 3. 2 Абсолюттік нөл . . .

3: 52

Белгілеулер мен қысқартулар . . .: 3. 3 Бойль-Мариотта заңы . . .

3: 57

Белгілеулер мен қысқартулар . . .: Қорытынды . . .

3: 62

Белгілеулер мен қысқартулар . . .: Пайдаланылған әдебиеттер тізімі . . .

3: 63

Белгілеулер мен қысқартулар . . .: Қосымша 1 . . .

3: 65

Белгілеулер мен қысқартулар . . .: Қосымша 2 . . .

3: 69

Белгілеулер мен қысқартулар . . .: Қосымша 3 . . .

3: 72

Белгілеулер мен қысқартулар

1 моль= 12 көміртек атомына тең бөлшектер саны.

1 кПа= $10^{- 3}$ $Па$

1 МПа= $10^{6}$ $Па$

1 $℃$ =+273. 15 $K$

$\pi$ =3, 14

1 л=1 $м^{3}$

1см= $м^{2}$

ПӘК = пайдалы әсер коэффициенті

$K^{- 1} = \frac{1}{K}$

1см = $\ 10^{- 2}$

1мл = $10^{- 3}$ л

1г = $10^{- 3}$ кг

1мг = $10^{- 3}$ г

1кДж = $10^{- 3}$ Дж

1мм = $10^{- 3}$ м

Кіріспе

Тақырыптың өзектілі: Адамдар ертеден суық пен ыстықтың ара-жігін айырып, температураны дененің жылыну дәрежесін сипаттайды деп есептеген. Жылу жайлы ғылымның дамуы температураны өлшеуге арналған құрал-термометр пайда болуымен басталады. Ең алғашқы термометрді 16 ғасырдың соңында Галилей жасады деп есептелінеді. Термодинамика механикалық жұмыс жасауға дененің ішкі энергиясын пайдаланудың негізгі тәсілдерін зерттейтін эмперикалық ғылым ретінде пайда болды.

Денелердің әртүрлі қасиеттері мен зат күйінің өзгерістері термодинамикада зерттелінеді. Термодинамика денелер мен табиғат құрылғысының тек макраскопиялық қасиеттерін зерттейді. Сонымен қатар физика ғылымындағы жылулық жұмыс және басқа энергия түрлерімен арадағы қарым-қатынасын зерттейтін тармағы. Тәжірибеден жинақталған нәтижелерге сүйенетін феноменологиялық ғылым. Ол көптеген құрамдас бөліктерден тұратын макраскопиялық жүйелер-термодинамикалық жүйелерді зерттейді. Мұндай жүйелерде жүретін процестер макраскопиялық шамалар, мысалға қысым және температура арқылы сипатталады, олар молекулалық деңгейге қолдануға келмейді.

Термодинамиканың негізгі ұғымдары: термодинамикадағы негізгі заңдар, газдардың молекула кинетикалық теориясы және фазалық өзгерістері мен термодинамиканың нақты газдарын толығырақ айтып түсіндіру.

Термодинамика лабораториясының құрамына кіретін құрылғылармен материалдардың жылулық қасиеттерін тәжіриебе жүзінде зерттеу жұмыстарын жүргізу. Металдар мен берілген жылуды сумен салысырып жылдың нақты мәндерін есептеу. Жылу тасымалдаушы мен температураның өзгеруі арасындағы қатынас туралы түбегейлі түсінік қалыптастырып, температура мен жылу арасындағы қатынастар мен судың балануының жасырын қызуын ақықтау.

Температураның қасиеттерін жан-жақты сипаттайтын зерттеу жұмыстары жүргізу. .

Жұмыстың мақсаты: Термодинамиканың әдістерін меңгеру.

Жұмыстың жаңалығы: Термодинамиканың лабораториядағы қондырғылар алғашқы рет жүйелі түрде қарастырылады.

Тәжірибелік құндылы: Термодинамика лабораториясында өткізілетін оқу процесінде қолданылады.

Дипломдық жұмыстың құрылымы : Дипломдық жұмыс кіріспеден, үш бөлімнен, қорытындыдан, пайдаланылған әдебиеттер тізімінен және қосымшадан тұрады. 35 сурет, 9 кесте бар. Әдебиеттер тізімі 27 және жұмыстың жалпы көлемі 64 бетті құрайды.

1 Термодинамиканың негізгі ұғымдары

1. 1 Идеал газдардың молекула-кинетикалық теориясы

Бізді қоршаған ортадағы денелер негізінен тоқсаннан астам біртекті атомдардан тұрады. Біртекті атомдардан құралған заттарды химиялық элементтер деп атайды. Оларға сутегі, көміртегі, күміс т. б. жатады. Атомдар бір-біріне тартылады. Осы тартылыстың нəтижесінде атомдар бірігіп, тұрақты күйге енеді. Яғни молекула түзеді. Ал бірдей молекулалардан құралған заттарды қосылыс деп атайды. Мұндай қосылыстарға, мысалы, су ( $H_{2}$ О), ас тұзы (NaCl) т. б. жатады. Заттың кішкене бір бөлігін бөлшек деп атайды. Біздің күнделікті көріп жүрген затымыз макроскопиялық деп есептеледі. Басқаша айтқанда, өте көптеген бөлшектерден тұрады.

Макроскопиялық заттар бір-біріне қарағанда реттелген түрде қозғалуы мүмкін. Оны механикада динамикалық қозғалыс деген атпен қарастырады. Бұл қозғалыстың басты ерекшелігі ретсіздігінде болып отыр. Осындай қозғалыс заңдылығын статистикалық деп атайды. Денелер өте көптеген макроскопиялық бөлшектерден құралғанда статистикалық заңдылық күшіне енеді $\lbrack 5\rbrack$ .

Макроскопиялық денелерді құрайтын бөлшектердің ретсіз қозғалысын жылулық қозғалысы деп атайды. Жылулық қозғалысы арқылы əрбір макроскопиялық дененің ішкі күйі анықталады. Макроскопиялық денені құрайтын бөлшектер ретсіз қозғалыста болатындықтан, олар бірімен-бірі соқтығысып отырады.

Макроскопиялық дененің тепе-теңдік күйде болуы оның кез келген бөлігінде температура бірдей екендігін білдіреді. Ал макроскопиялық дененің əр бөлігіндегі температура түрліше болса, онда энергия оның бір бөлігінен екінші бөлігіне беріледі. Демек температура - макроскопиялық дене бөлшегінің жылулық қозғалысының интенсивтілігін көрсететін шама. Дененің температурасын өлшеу үшін термометрлер пайдаланылады. $\lbrack 3\rbrack$ .

Макроскопиялық дененің күйін анықтайтын келесі параметр - қысым. Газ немесе сұйық молекулалары тəртіпсіз қозғалған кезде олар тек бірімен-бірі соқтығысып қана қоймай, сонымен қатар, ыдыс қабырғасымен де соқтығысады. Макроскопиялық бөлшектердің ыдыс қабырғаларына соққылау күшінің орташа мəні қысым деп аталады.

Сонымен, макроскопиялық денені қысым р, көлем V жəне температура T сипаттайды. Осы үшеуінің арасындағы байланысты анықтайтын мына формуланы $f\ (p, V, T) = 0$ макроскопиялық дене күйінің теңдеуі деп атайды.

Газ тəрізді заттарда молекулалар мен атомдар бір-бірінен қашығырақ орналасады. Өзара əсерлесу күші тек молекулалардың соқтығысуы кезінде пайда болады. Демек молекулалық күштердің əрекеті тек соқтығысқан молекулалардың энергия алмасуы кезінде ғана байқалады. Сонымен, ыдыстағы газ молекулаларының саны аз болса (тығыздығы аз), олардың бірімен-бірі соқтығысу мүмкіндігі азаяды. Осындай газды идеал газ дейді. Идеал газ деп молекулалар арасында өзара əсерлесу күштері болмайтын, жеке молекулалар көлемі ыдыс көлемімен салыстырғанда өте аз, тіпті оны еске алмауға да болатын жəне молекулалар арасындағы өзара соқтығысу абсолют серпімді болатын газдарды айтады $\lbrack 2\rbrack$ .

Бойль-Маритт заңы. Газ күйіндегі заттардың меншікті көлемі болмайды. Сондықтан газдар ыдысқа толтырылғанда, сол ыдыстың көлемін толық алып тұрады және қабырғаларына белгілі бір қысым күшін түсіреді. ХVII ғасыдың ортасында ағылшын ғалымы Р. Бойль (1627-1691) және француз физигі З. Мариттың (1620-1684) бір-біріне тәуелсіз жасаған тәжірибе қорытындылары температура тұрақты болғанда газ көлемінің $(V)$ оның қысымына $(p)$ тәуелді өзгеретінін тұжырымдады:

\frac{p_{1}}{p_{2}} = \frac{V_{2}}{V_{1}}, \ \ \ pV = const

(1. 1)

Бұл тəуелділікті изотерма деп аталатын гипербола қисығымен көрсетуге болады (1. 1 сурет) . Газ күйінің бір күйден екінші күйге тұрақты температурада өтуі изотермалық процесс деп аталады $\lbrack 3\rbrack$ .

1. 1 сурет - Изотерма (гипербола қисығы)

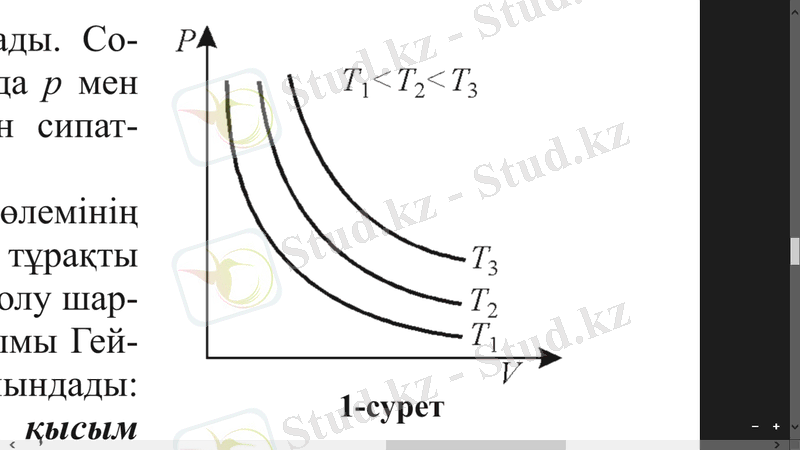
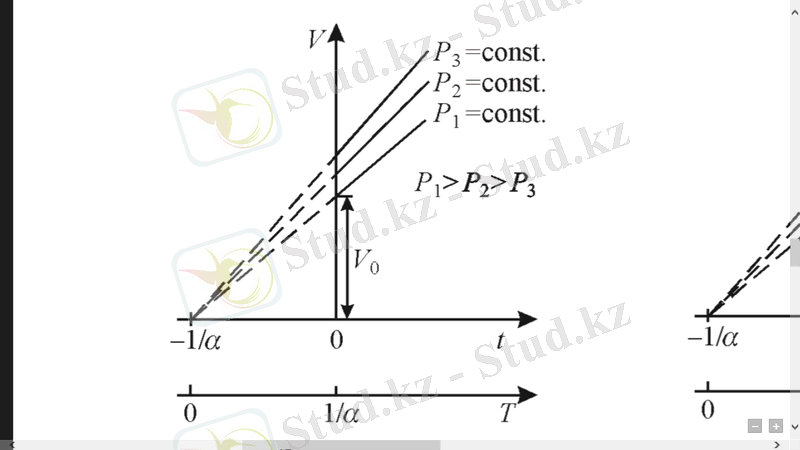
Гей-Люссак заңы. Газ көлемінің $(V)$ оның температурасына $(T)$ тұрақты қысымда $\ (p = const)$ тәуелді болу шартын бірінші рет француз ғалымы Гей-Люссак (1778-1850) тағайындады. Берілген газ массасы үшін қысым тұрақты болғанда, газ көлемі оның температурасына сызықты тәуелді өзгереді ( $p = const, \ m = const$ ) :

V = V_{0}(1 + \alpha_{v}t^{0})

(1. 2)

мұндағы: $V_{0}$ -газдың $0℃$ - тағы көлемі, $\alpha_{v}$ - газдың көлемдік ұлғаюының термиялық коэффициенті. Тұрақты қысымда газ көлемі мен температураның тәуелділігі графикте түзу сызықпен көрсетіледі. Қысымның әрбір мәніне сәйкес келетін түзу сызық изобара деп аталады (1. 2 сурет) $\lbrack 1\rbrack$ .

Шарль заңы. Тұрақты көлемде газ температурасының қысымға тəуелді болатыны да анықталады, яғни берілген газдың массасы үшін көлемі тұрақты болғанда, газ қысымы оның температурасына сызықты тəуелділікте өзгереді $(V = const, \ m = const)$ .

p = p_{0}(1 + \alpha_{\eth}t^{0})

(1. 3)

мұндағы: $p_{0}$ -газдардың 0 $℃$ - тағы қысымы термиялық коэффициенті. Көлем тұрақты болғанда, $\alpha_{\eth}$ - газ қысымының $p$ мен t тәуелділігі түзу сызықты және ол изохора деп аталады (1. 3 сурет) . Газ күйінің мұндай өзгеруін изохоралық процесс деп атайды. Зерттеудің нәтижелері газдардың термиялық коэффициенттері $a_{v}$ және $\alpha_{p}$ бір-біріне шамалас екенін көрсетеді, яғни:

a_{V} = a_{p} = a = \frac{1}{273. 15K} = 0. 00367K^{- 1}

(1. 4)

: 1. 2 сурет изобара түзі сызығы

: 1. 3 сурет изохора түзу сызығы

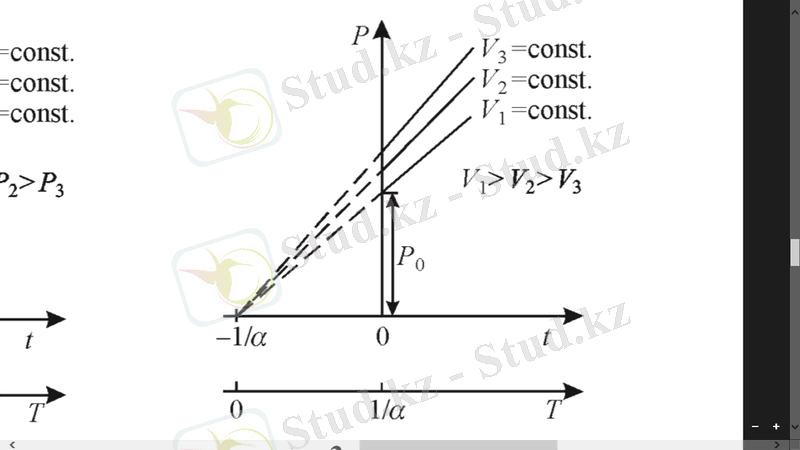
Изобара жəне изохора түзулері абсцисса осінде шамасы $t_{0} = \frac{1}{\alpha} = - 273. 15℃$ нүктесінде қиылысады. Температураның бастапқы санақ нүктесін осы нүктеге ауыстырып, температураның Цельсий шкаласынан абсолют Кельвин шкаласы деп аталатын басқа температуралық шкалаға өтуге болады $\lbrack 7\rbrack$ .

Абсолют температура T мен Цельсий бойынша анықталған t температураның қатынасы мынадай болады

T = t^{0} + \frac{1}{\alpha} = t^{0} + 273. 15.

(1. 5)

Мысалы, 0 $℃$ -қа +273, 15К сәйкес келеді. 0К-ге тең температура абсолют нөл деп аталады, оған -273, 15°С мəні сəйкес келеді. Енді (1. 4) жəне (1. 5) теңдеулерге абсолют температураның мəнін қойып, оны басқа түрде жазуға болады:

$\frac{V}{V_{0}} = 1 + \frac{t^{0}}{273. 15},$

бұдан V/ $V_{0}$ = T/ $T_{0}$ . Егер $V_{0}$ мен $Т_{0}$ тұрақты шама екенін ескерсек, онда изобаралық процесс үшін:

V/T=const.

(1. 6)

Осындай əдіспен изохоралық процесс үшін де мынадай теңдікті жазуға болады, яғни:

p/T=const.

(1. 7)

Авогадро тағайындаған заң бойынша бірдей жағдайларда, яғни бірдей температура мен қысымда барлық газдардың мольдерінің көлемі бірдей болады. Əртүрлі заттардың бір мольдегі молекулалар саны бірдей болады: $N_{A} = 6. 022 \bullet 10^{23}\ {моль}^{- 1},$ бұл Авогадро саны деп аталады $\ \lbrack 5\rbrack$ .

Ағылшын физигі жəне химигі Дж. Дальтон (1766-1844) тағайындаған заң бойынша идеал газдар қоспасының жалпы қысымы сол қоспаны құрайтын газдардың парциал қысымдарының қосындысына тең болады, яғни:

p = p_{1} + p_{2} + p_{3}{+ \ldots + p}_{n}

(1. 8)

мұндағы: $p_{1}, p_{2}, p_{3}{, \ldots, p}_{n}$ - парциал қысымдар.

Клапейрон-Менделеев теңдеуі. Массасы $m$ газдың алғашқы күйін сипаттайтын параметрлердің мəндері $p_{0}, \ \ V_{0}, {\ T}_{0}$ болсын. Егер газдың күйі өзгерсе, онда оның соңғы күйін сипаттайтын параметрлер $p_{1}, {\ V}_{1}, {\ T}_{1}$ болады. Бойль-Мариотт жəне Гей-Люссак заңдары негізінде осы газдың екі күйінің арасындағы байланысты анықтауға болады. Ол үшін газдың бірінші күйдегі қысымын тұрақты деп $p_{0} = const,$ оны, $T_{0} - ден\$ $T_{1} - ге$ дейін қыздырамыз. Сонда оның көлемі $V_{0}$ - ден $V^{, }$ -ке дейін өзгереді. Бұл процесс изобаралық болғандықтан, Гей-Люссак заңы бойынша көлемнің өзгеруі: $V^{, } = V_{0}(T_{1}/T_{0})$ . Енді газ күйінің соңғы өзгерісін тұрақты температурада $(T = const)$ , көлемін өзгертіп байқауға болады: яғни газ қысымы $p_{0}$ -ден $p_{1}$ -ге дейін өзгерсе, онда көлемі $V^{, }$ -тен $V_{1}$ - ге дейін ұлғаяды. Бұл өзгеріс изотермалық болғандықтан, Бойль-Мариотт заңы негізінде:

V^{, } = p_{1}(V_{1}/p_{0})

Сонымен, берілген газ массасы үшін, газ күйінің өзгерісін көрсететін шама $pV/T\$ әр уақытта тұрақты болады, яғни:

\frac{pV}{T} = const

(1. 9)

Бұл теңдікті бірінші рет француз ғалымы және инженер Б. Клапейрон (1799-1864) Бойль-Мариотт және Гей-люссак заңдарын біріктіріп қорытып шығарғандықтан, ол идеал газ күйін сипаттайтын Клапейрон теңдеуі деп аталады $\lbrack 8\rbrack$ . Сондықтан газдың сандық мəні бір мольге тең болса, (1. 9) теңдіктегі тұрақты шама барлық газдар үшін бірдей болады. Барлық газ үшін тұрақты шаманы R əрпімен белгілеп, оны универсал газ тұрақтысы деп атайды. Сонда (1. 9) теңдік мына түрде жазылады:

\left( pV_{\mu} \right) = RT

(1. 9 a)

Енді (1. 9а) теңдеуден универсал газ тұрақтысының сандық мәнін анықтап шығарайық. Егер $T = 273\, \ 15\$ К, $p = 1. 01 \bullet 10^{2}\ \$ кПА, $V_{\mu} = 22. 41 \bullet {\bullet 10}^{- 3}м^{3}/моль$ , болса, онда:

R = \frac{1. 01 \bullet 10^{5} \bullet 22. 41 \bullet 10^{- 3}}{273} = 8. 31Дж/(моль \bullet K)

1 мольде ғана дұрыс болатын ${pV}_{0} = RT, \ (V_{0} = V_{\mu})$ формуланы кез келген мөлшердегі массаға қолданатындай өзгертіп жазуға болады. Ол үшін газдың молярлық массасын $\mu$ әріпімен белгілейміз. Олай болса, тұрақты қысым мен температурада $(p_{1}T = const)$ :

$V_{\mu} = \frac{V_{0}m}{\mu}, \ \ pV_{0}\frac{m}{\mu} = \frac{m}{\mu}RT, \ \ pV_{\mu} = \frac{m}{\mu}RT.$

Бұл теңдік массасы $m$ кез келген газ үшін қорытылып шығарылған Клапейрон менделеев теңдеуі болып табылады.

Vμ=V0mμ,pV0mμ=mμRT,pVμ=mμRT.V_{\mu} = \frac{V_{0}m}{\mu}, \ \ pV_{0}\frac{m}{\mu} = \frac{m}{\mu}RT, \ \ pV_{\mu} = \frac{m}{\mu}RT.Бұл теңдік массасыmmкез келген газ үшін қорытылып шығарылған Клапейрон менделеев теңдеуі болып табылады.: Универсал газ тұрақтысы. Жеңіл қозғалатын поршені бар цилиндрлі ыдыста көлемі 1 моль газ болсын (1. 4 сурет) . Газ жылжымалы поршеньге сыртқы қысымға тең

p = const

қысым түсіреді. Цилиндр ішіндегі газды 1 К температураға дейін қыздырса, оның көлемі ұлғайып, поршеньді

h\

биіктікке көтереді. Поршеньге түсіретін қысым

\ p = F/S

. Мұндағы -поршенге түсірілген қысым күші,

S

- поршенің ауданы. Сонда қысым күші:

F = p \bullet S

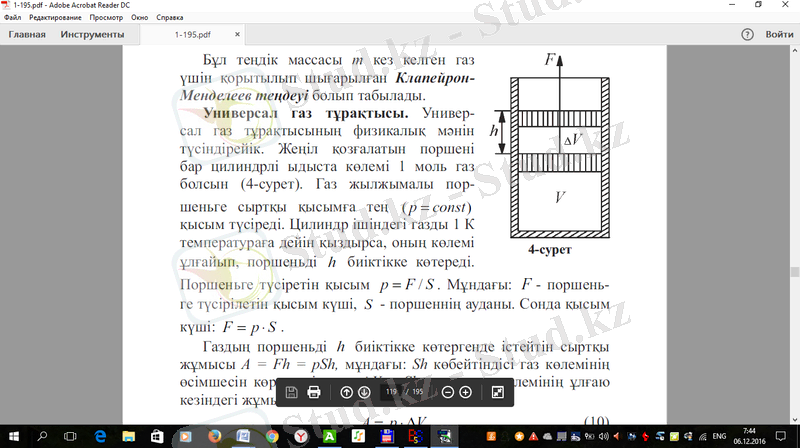
1. 4 сурет

Газдың поршеньді $h\ \ \$ биіктікке көтергенде істейтін сыртқы жұмысы $\ A = Fh = pSh$ , мұндағы: $\ Sh$ көбейтіндісі газ көлемінің өсімшесін көрсетеді, яғни $\mathrm{\Delta}V = Sh$ , сонда газ көлемінің ұлғаю кезіндегі жұмыс:

A = p \bullet \mathrm{\Delta}V

(1. 10)

Егер газдың алғашқы күйін сипаттайтын теңдеу

pV = RT

(1. 11)

болса, 1 K қыздырғаннан кейінгі көлемі $V_{1}$ -ге өзгеріп, (1. 11) теңдеуі басқа түрде көрсетіледі, яғни:

pV_{1} = R(T + 1) .

(1. 12)

Соңғы (1. 11) және (1. 12) теңдеулерден мына теңдік шығады:

p\left( V_{1} - V \right) = R, \ \ \ p\mathrm{\Delta}V = R.

(1. 13)

Егер де (1. 10) және (1. 13) теңдеулерді салыстырсақ, онда универсал газ тұрақтысы істелген жұмысқа тең болады:

A=R

(1. 14)

Сонымен, универсал газ тұрақтысы 1 моль газды 1 К температураға қыздыру үшін кеткен изобаралық жұмысқа тең екен $\lbrack 9\rbrack$ .

1. 2 Термодинамика заңдары.

Больцманның таралу заңы. Молекулалар санының биіктік бойынша өзгеруін, барометрлік формула арқылы анықтауға болады.

p_{1} = p_{0}e^{- \frac{g\mu}{RT}(h_{1} - h_{0}) }

(1. 15)

Егер $T = const\$ $p_{1}/p_{0} = \frac{n_{1}}{n_{0}}$ , бұдан (1. 15) теңдеуін мына түрде жазуға болады:

n_{1} = n_{0}e^{- \frac{\mu g}{RT}(h_{1} - h_{0}) }

(1. 16)

$R/\mu = k/m$ екенін ескеріп, соңғы теңдеуді былайша жазамыз:

n_{1} = n_{0}e^{- \frac{gm}{kT}(h_{1} - h_{0}) }

(1. 17)

Осы формуланың mg( $h_{1} - h_{0}$ ) көрсеткішін газ бөлшектерінің $h_{0}$ - ден $h_{1}$ биіктікке көтерілген кездегі потенциалдық энергиясының өзгерісі деп есептейік: mg( $h_{1} - h_{0}$ ) = $\mathrm{\Delta}E_{p} = E_{p_{1}} - E_{p_{0}}$ . Бұдан (1. 17) теңдік мынадай түрге келеді : $\ n_{1} = n_{0}e^{\mathrm{\Delta}E_{p}/kT}$ немесе $\overline{n} = n_{1}/n_{0}$ қатынасын енгізіп, мына түрге келтіреміз:

\overline{n} = e^{- \frac{\mathrm{\Delta}E_{p}}{kT}}

(1. 18)

мұндағы: $\ \overline{n}$ - молекулалардың салыстырмалы саны. (1. 18) формула Больцманның таралу заңы деп аталады. Бұл өрнек сыртқы күштердің потенциалдық өрісіндегі бөлшектердің таралуын сипаттайды жəне бұл теңдеуден температура төмендегенде, нөлге тең емес биіктікте бөлшектер саны азайып, ал $T = 0\$ жағдайында $n = 0$ болатыны $\$ байқалады. Сөйтіп, абсолют нөлде барлық бөлшектер Жер бетінде орналасқан болар еді. Жоғары температурада, керісінше, биіктікке көтерілген сайын $n$ баяу кемиді, яғни молекулалар биіктікке көтерілген сайын біркелкі таралады. Мұның физикалық мəні мынадай: біріншіден, молекулалардың жерге таралуы $(mg)$ нəтижесінде олар жер бетінде орналасуға ұмтылады, екіншіден, молекулалардың жылулық қозғалысы оларды барлық биіктік бойынша біркелкі таратуға тырысады. Молекулалар массасы m үлкен болса, $T$ аз болған сайын молекулалар жер бетіне таяу қоюлана түседі. Егер $T = 0$ болса, шектік жағдайда жылулық қозғалыс толық тоқтап, молекулалар тартылыстың əсерінен жер бетінде орналасады. $\lbrack 10\rbrack$ . Больцманның таралу заңының Максвелдің жылдамдықтар бойынша таралуының экспоненциалдық мүшесімен ұқсас екенін байқаймыз: