Математикалық талдаудың элементтерінің қолданылуы және қолданбалы есептер


Қазақстан Республикасы білім және ғылым министірлігі
«Ш. Уәлиханов атындағы Көкшетау мемлекеттік университеті» ШЖҚ РМК
Ережеп Мария
Математикалық талдау элементтерінің қолданыстары.
ДИПЛОМДЫҚ ЖҰМЫС
Мамандығы 5В010900-Математика
Көкшетау 2018
Қазақстан Республикасы білім және ғылым министірлігі
«Ш. Уәлиханов атындағы Көкшетау мемлекеттік университеті» ШЖҚ РМК
ДИПЛОМДЫҚ ЖҰМЫС
Тақырыбы: Математикалық талдау элементтерінің қолданыстары.
Мамандығы 5В010900-Математика
Орындады:
Ғылыми жетекші,
п. ғ. к., доцент:
«Қорғауға жіберілді»
Кафедра меңгерушісі
Көкшетау 2018
МАЗМҰНЫ
КІРІСПЕ . . .
1 МАТЕМАТИКАЛЫҚ ТАЛДАУДЫҢ НЕГІЗГІ ҰҒЫМДАРЫНА ҚЫСҚАША ШОЛУ . . .
1. 1Бір айнымалыға тәуелді функциялардың дифференциалдық есептеулері . . .
1. 2 Алғашқы функция және анықталмаған интеграл, оның негізгі қасиеттері мен есептеу әдістері . . .
2 МАТЕМАТИКАЛЫҚ ТАЛДАУ ЭЛЕМЕНТТЕРІНІҢ ҚОЛДАНЫСТАРЫ . . .
2. 1Туынды және оның қолданылуы . . .
2. 1. 1 Физикадағы қолданыстары . . .
2. 1. 2 Құрылыстағы қолданыстары . . .
2. 1. 3 Ағаш өңдеу есептері . . .
2. 1. 4 Автомобиль жолдарына байланысты есеп . . .
2. 1. 5 Мелиорация есептері . . .
2. 2 Интеграл және оның қолданылуы . . .
2. 2. 1 Геометрияның аудан және көлем есептеу формулаларын анықталған интеграл арқылы қорыту . . .
2. 2. 1. 1 Айналу бетінің ауданы.
2. 2. 1. 2Сфера мен оның бөліктерінің ауданы 22
2. 2. 1. 3Доғаның ұзындығы 23
2. 2. 1. 4Дененің көлемін оның параллель қималарының аудандары
бойынша есептеу 25
2. 2. 1. 5Тік дөңгелек конустың көлемі 27
2. 2. 1. 6Шар мен оның бөліктерінің көлемі 30
2. 2. 1. 7 Кез келген цилиндрдің көлемі 34
2. 2. 1. 8Пирамданың көлемі 34
2. 2. 1. 9Айналу денесінің көлемі
2. 2. Физикадағы қолданыстарына байланысты есептер . . .
2. 3 Дифференциалдық теңдеулер нақтылы процестердің математикалық модельдері . . .
ҚОРЫТЫНДЫ . . .
ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР . . .
КІРІСПЕ
Зерттеу тақырыбының өзектілігі.
Елбасы Н. А. Назарбаевтың Еуразия ұлттық университетінде оқыған лекциясында: «Білімді, сауатты адамдар-бұл ХХІ ғасырда адамзат дамуының негізгі қозғаушы күші»-деп аталған [1] .
«Қазақстан Республикасында білім беруді дамытудың 2016-2020 жылдарға арналған Мемлекеттік бағдарламасында» белгіленген орта білім берудің негізгі міндеттерінің бірі « . . . білім алушылардың еңбек нарығындағы бәсекеге қабілеттілігін қамтамасыз ету үшін кәсіптік дағдылар алуына жағдай жасау болып табылады . . . »-деп көрсетілген [2] .
Бүгінде, күн өткен сайын, білім мен ғылымы дамыған елдер барлық жағынан алда болатынына көз жеткізудеміз.
Өткен ғасырдың өзінде, осы замандағы iрi физиктердiң бiрi, немiс ғалымы Гейзенберг табиғат заңдарын танып бiлудегi математиканың ролiн былай сипаттайды: «сегiз қырлы математика кейде физиктердiң ойында жоқ жерден жаңалықтар ашуға көмек көрсетедi» [3] . Оның математика ғылымына бұлайша баға беруiнде бiр себеп бар. 1925 жылы Гейзенберг атомның құрылысымен байланысты бiр теорияны математикалық әдiспен зерттеу үстiнде күтпеген жаңалық ашқан болатын. Ол жаңалық - атом құрылысы жөнiндегi Бор теориясының кемшiлiктерiне түзету енгiзе отырып жаңа кванттық механиканы жасауға негiз болды. Осы жаңалықты ашумен байланысты Гейзенберг былай деп жазған болатын: «Математика физикадан гөрi «ақылдырақ» болды, өйткенi математиканың көмегiмен жаңа тәуелдiлiктердiң iзiне түстiк» [3] .
Физиктер тек сутегi мен гелийдiң ғана атомдарының модельдерiн жасады. Бұл элементтердiң атомдарының ядросын айнала бiр немесе екi электрон қозғалады. Бұлардан басқа химиялық элементтердiң атомдарының құрылысы туралы жалпы түсiнiк берiлгенi болмаса, толық математикалық есептеу жасалған жоқ.
Қозғалыс, айнымалы шамалар және олардың өзара байланыстары бізді айнала қоршап тұр. Қозғалыстардың әр түрлері және олардың заңдылықтары нақты ғылымдардың-физиканың, геологияның, биологияның, социологияның және т. б. -қарастыратын негізгі объектісін құрайды. Сондықтан, сандық қатынастарды сипаттау үшін сандар мен арифметика қаншалықты қажет болса, нақты тіл және айнымалы шамаларды сипаттайтын және қарастыратын математикалық әдістер ғылымның барлық салаларында соншалықты қажет болады.
Тілдің және айнымалы шамалардың және олардың өзара байланыстарын сипаттайтын математикалық әдістердің негізін математикалық талдау құрайды. Бүгінгі күнге дейін математикалық талдаудың көмегімен космостық траекторияны, ядролық реактордың жұмысын, мұхит толқынының жүгірісін, циклонның даму заңдылықтарын, т. б. табиғи процестерді анықтаған еді. Қазіргі кезде математикалық талдаудың көмегінсіз шаруашылықты басқару, ресурстарды тиімді орналастыру, технологиялық процестерді ұйымдастыру, химиялық реакциялардың ағымын алдын-ала болжау немесе табиғаттағы өзара байланыста болатын жануарлар мен өсімдіктердің санының өзгеруін алдын-ала болжай алмаймыз, себебі аталған процестердің бәрі-динамикалық процестер.
XVII ғасырда пайда болған математикалық талдау элементтері бізге айнымалы шамаларды және қозғалыстарды сандық және сапалық түрде қарастыруға, ғылыми тұрғыдан сипаттауға кең мүмкіндіктер ашты.
Бұл мүмкіндіктерді зерттеп білу үшін, математиканың математикалық талдау элементтерін терең меңгеру қажеттілігін туындатады[4] .
Жоғарыда сипатталған құбылыстар үнемі өзгерістегі процестер болғандықтан, таңдалған тақырыбымыз да ғылыми зерттеулердің күн тәртібінен түспейді.
Диплом жұмысының мақсаты- математикалық талдау элементтерінің қолданыстарын көрсету.
Диплом жұмысының міндеті -математикалық талдау элементтерінің қолданыстарын көрсетудің тиімді формасы-бұл қолданбалы бағыттағы есептерді қарастыру.
Диплом жұмысының практикалық маңыздылығы -жұмыстың өне бойында қарастырылған есептерді, мектеп мұғалімдері сабақ процесінде қолдана алады.
Диплом жұмысы кіріспе, екі тараудан, қорытынды және пайдаланған әдебиеттер тізімінен тұрады.
1 МАТЕМАТИКАЛЫҚ ТАЛДАУДЫҢ НЕГІЗГІ ҰҒЫМДАРЫНА ҚЫСҚАША ШОЛУ 1. 1 Бір айнымалыға тәуелді функциялардың дифференциалдық есептеулері[5] - [7] .
Айталық,
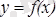 функциясы
функциясы
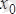 нүктесінде және оның маңайында анықталған болсын.
нүктесінде және оның маңайында анықталған болсын.
Анықтама.
Аргумент
 -тің
-тің
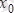 нүктесіндегіөсімшесі деп
нүктесіндегіөсімшесі деп
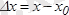 айырмасын атайды
.
айырмасын атайды
.
Анықтама.
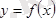 функцияның
функцияның
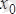 нүктесіндегі өсімшесі деп
нүктесіндегі өсімшесі деп
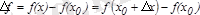 айырмасын айтады.
айырмасын айтады.
Анықтама.
Егер
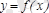 функциясы
функциясы
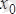 нүктесінің маңайында анықталған және
нүктесінің маңайында анықталған және
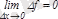 болса
,
онда ол
болса
,
онда ол
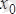 нүктесінде үзіліссіз деп аталады
.
нүктесінде үзіліссіз деп аталады
.
Шындығында да
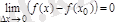

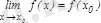 .
.
Анықтама.
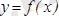 функциясының
функциясының
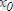 нүктесіндегі туындысы депақырлы шегін айтады.
нүктесіндегі туындысы депақырлы шегін айтады.
Бұл туынды мына символдардың бірімен белгіленеді:
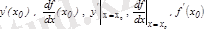 .
.
Егер
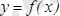 функциясының
функциясының
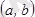 интервалының әрбір нүктесінде туындысы болса, онда оны осы интервалда дифференциалданады дейді. Туындыны табу амалын дифференциалдау дейді.
интервалының әрбір нүктесінде туындысы болса, онда оны осы интервалда дифференциалданады дейді. Туындыны табу амалын дифференциалдау дейді.
Теорема.
Егер
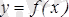 функциясы
функциясы
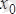 нүктесінде дифференциалда-натын функция болса
,
онда ол бұл нүктеде үзіліссіз болады
.
нүктесінде дифференциалда-натын функция болса
,
онда ол бұл нүктеде үзіліссіз болады
.
Ескерту: теорема керісінше дұрыс емес.
Туындының геометриялық мағынасы.
:
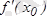 туындысы
туындысы
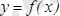 функциясыныңграфигіне
функциясыныңграфигіне
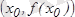
. :
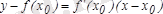 .
.
. Егер
 ,
,
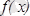 -, онда
-, онда
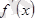 дененің
дененің
 .
.
. , кейбірэлементар (қарапайым) .
1. Көрсеткіштік функция
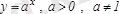
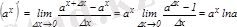 .
.
Дербес жағдайда
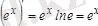 .
.
2. Тригонометриялық функциялар
 .
.
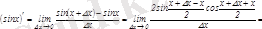
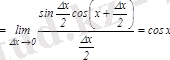
Дәл осылай
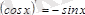 .
.
2. Дәрежелік функция
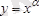 .
.
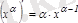
Дербес жағдайда,
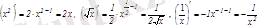 .
.
Теорема 1.
(қосындыны, -циалдауережелері) . Егер
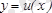 және
және
 , , (қатынастыңбөлімі
, , (қатынастыңбөлімі
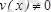 ) :
) :
1.
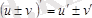
2.
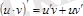
3.
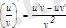 .
.
.
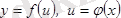 . Сондакүрделі
. Сондакүрделі
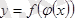 функциясыныңтуындысы:
функциясыныңтуындысы:
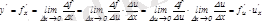 .
.
Сонымен
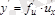 .
.
.
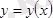 жәнеоғанкері
жәнеоғанкері
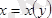 функция-лары
функция-лары
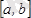 . :
. :
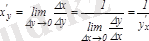 .
.
Сонымен
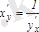
болады.
Негізгі элементар функциялар туындыларының кестесі
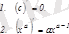
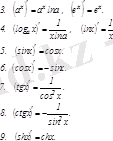
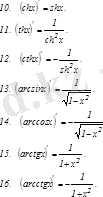
Жоғары ретті туындылар мен дифференциалдар. Жоғары ретті туындылар және дифференциалдар.
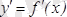 берілген
берілген
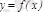 функциясының бірінші немесе бірінші ретті туындысы, ал функцияның өзі нөлінші ретті туынды деп аталады.
функциясының бірінші немесе бірінші ретті туындысы, ал функцияның өзі нөлінші ретті туынды деп аталады.
Анықтама.
Функцияның
 -
(
-
(
 -1
) -
-1
) -
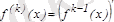 ,
,
 =1, 2, 3, …,
егероларбарболса, онда
=1, 2, 3, …,
егероларбарболса, онда
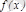 функциясы
функциясы
 -.
-.
Мысал.
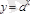 функциясыберілген. Біріншітуындысы
функциясыберілген. Біріншітуындысы
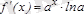 ,
,
екінші туындысы
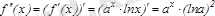 ,
,
үшінші туындысы
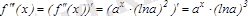 .
.
Демек,
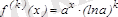 ,
,
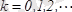 .
.
Егер
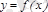 және
және
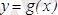 функциялары
функциялары
 -рет дифференциалданатын болса, онда (
-рет дифференциалданатын болса, онда (
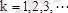 ), мына ережелер орынды:
), мына ережелер орынды:
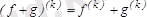 ,
,
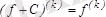 .
.
2. Лейбниц формуласы:
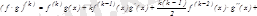
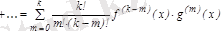 ;
;
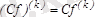 .
.
Айталық
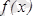 функциясы
функциясы
 -рет дифференциалданатын болсын.
-рет дифференциалданатын болсын.
Анықтама.
Функцияның
 -ші дифференциалы деп оның (
-ші дифференциалы деп оның (
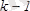 ) -ші ретті дифференциалының дифференциалын айтады:
) -ші ретті дифференциалының дифференциалын айтады:
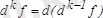 .
.
Дифференциалды есептеу формулаларын келтірейік:
 ,
,
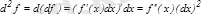 ,
,
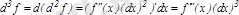
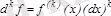 .
.
 -шы ретті дифференциалдар үшін мына ережелер орынды:
-шы ретті дифференциалдар үшін мына ережелер орынды:
1)
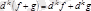 ,
,
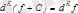 .
.
2)
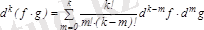 ,
,
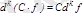 .
.
Ескерту:
Жоғарғы ретті
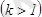 дифференциал формасы инвариантты емес.
дифференциал формасы инвариантты емес.
Анықтама.
Егер
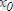 нүктесініңбір маңайында
нүктесініңбір маңайында
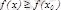
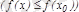 тең-сіздігі орындалса, онда
тең-сіздігі орындалса, онда
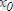 нүктесін
нүктесін
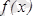 функциясының жергілікті минимум (максимум) нүктесі деп атайды. Жергілікті минимум және жергілікті максимум нүктелері жергілікті экстремум нүктелері деп аталады. Ал осы нүктелердегі функцияның мәні функцияның экстремумы деп аталады.
функциясының жергілікті минимум (максимум) нүктесі деп атайды. Жергілікті минимум және жергілікті максимум нүктелері жергілікті экстремум нүктелері деп аталады. Ал осы нүктелердегі функцияның мәні функцияның экстремумы деп аталады.
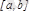 кесіндісінде анықталған функцияның тек қана бір ең үлкен және ең кіші мәндері болады, ал максимумдар және минимумдер бірнеше болуы мүмкін. Функцияның кейбір максимумдары оның минимумдарынан кіші болуы да мүмкін.
кесіндісінде анықталған функцияның тек қана бір ең үлкен және ең кіші мәндері болады, ал максимумдар және минимумдер бірнеше болуы мүмкін. Функцияның кейбір максимумдары оның минимумдарынан кіші болуы да мүмкін.
Ферма теоремасы.
Егер
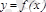 функциясы
функциясы
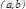 интервалында диффе-ренциалданатын болса және
интервалында диффе-ренциалданатын болса және
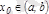 нүктесінде ең үлкен немесе ең кіші мәнін қабылдайтын болса, онда функцияның туындысы бұл нүктеде нөлге тең, яғни
нүктесінде ең үлкен немесе ең кіші мәнін қабылдайтын болса, онда функцияның туындысы бұл нүктеде нөлге тең, яғни
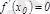 .
.
Геометриялық мағынасы:
функцияның максимум және минимум нүктелерінде жүргізілген жанама
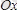 өсіне параллель болады.
өсіне параллель болады.
Ролль теоремасы.
Егер
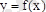 функциясы:
функциясы:
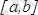 кесіндісінде үзіліссіз болса,
кесіндісінде үзіліссіз болса,
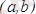 интервалында дифференциалданатын болса және
интервалында дифференциалданатын болса және
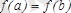 болса, онда ең болмағанда бір
болса, онда ең болмағанда бір
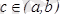 нүктесі табылып,
нүктесі табылып,
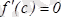 болады.
болады.
Геометриялық мағынасы:
егер теорема шарттары толығымен орындалса, онда
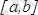 кесіндісінде жататын ең болмағанда бір
кесіндісінде жататын ең болмағанда бір
 нүктесі табылып, сол нүктеде жүргізілген жанама
нүктесі табылып, сол нүктеде жүргізілген жанама
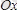 өсіне параллель болады.
өсіне параллель болады.
Kоши теоремасы.
Егер
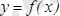 және
және
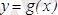 функциялары
функциялары
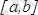 ке-сіндісінде үзіліссіз болса,
ке-сіндісінде үзіліссіз болса,
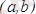 интервалында дифференциалданатын болса және
интервалында дифференциалданатын болса және
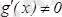
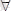
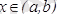 , онда ең болмағанда бір
, онда ең болмағанда бір
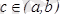 нүктесі табылып
нүктесі табылып
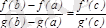
теңдігі орындалады .
Л
агранж теоремасы.
Егер
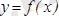 функциясы
функциясы
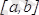 кесіндісінде үзіліссіз болса,
кесіндісінде үзіліссіз болса,
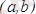 интервалында дифференциалданатын болса онда
интервалында дифференциалданатын болса онда
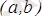 интервалында жататын
интервалында жататын
 нүктесі табылып,
нүктесі табылып,
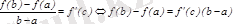 теңдігі орындалады.
теңдігі орындалады.
Геометриялық мағынасы:
мына қатынас
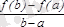
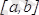 кесін-дісінде
кесін-дісінде
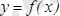 функциясының графигінің шеткі нүктелерін қосатын хорданың
функциясының графигінің шеткі нүктелерін қосатын хорданың
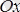 өсінің оң бағытымен жасайтын бұрыштың тангесіне тең, ал
өсінің оң бағытымен жасайтын бұрыштың тангесіне тең, ал
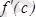
 нүктесіне жүргізілген жанаманың
нүктесіне жүргізілген жанаманың
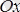 өсінің оң бағытымен жасайтын бұрышының тангенісіне тең. Лагранж теоремасы бойынша
өсінің оң бағытымен жасайтын бұрышының тангенісіне тең. Лагранж теоремасы бойынша
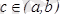 нүктесінде олар өзара тең болады, яғни қиюшы мен жанама параллель болады.
нүктесінде олар өзара тең болады, яғни қиюшы мен жанама параллель болады.
Лопиталь ережесі.
Бұл ереже
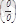 немесе
немесе
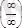 анықталмағандықтарын есептеуге мүмкіндік береді.
анықталмағандықтарын есептеуге мүмкіндік береді.
Теорема.
Айталық,
 нүктесінің маңайында
нүктесінің маңайында
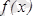 және
және
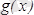 функциялары анықталған және дифференциал-данатын болсын (нүктенің өзінде бұл шарттар орындалмауы да мүмкін) және
функциялары анықталған және дифференциал-данатын болсын (нүктенің өзінде бұл шарттар орындалмауы да мүмкін) және
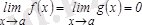 ,
,
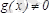 ,
,
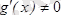 .
.
Егер
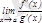 шегі бар болса, онда
шегі бар болса, онда
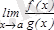 шегі бар болады және мына теңдік орындалады:
шегі бар болады және мына теңдік орындалады:
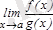 =
=
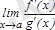 .
.
Осысияқты тұжырымдар
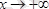 ,
,
 ,
,
 ,
,
 ,
,
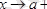
жағдайларда да орынды.
Функцияның дифференциалы.
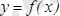 функциясының шектелген туындысы бар болсын, онда:
функциясының шектелген туындысы бар болсын, онда:
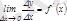 ,
,
демек
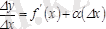
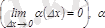 шексіз аз шама.
шексіз аз шама.
Онда функцияның өсімшесі былай жазылады:
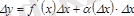 .
.
Осы теңдікте екінші қосылғыш
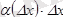 ,
,
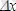 ке қарағанда жоғарғы ретті шексіз аз шама болғандықтан, бірінші қосылғыш
ке қарағанда жоғарғы ретті шексіз аз шама болғандықтан, бірінші қосылғыш
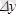 ке эквивалентті шама болады.
ке эквивалентті шама болады.
Анықтама.
Функцияның туындысының аргументтің өсімшесіне көбейтіндісін дифференциал деп атайды және мына түрде жазады:
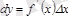 . Дербес жағдайда, егер
. Дербес жағдайда, егер
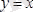 болса, онда
болса, онда
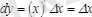 , осыдан
, осыдан
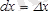 және осыны пайдаланып дифференциалдың формуласын былай жазуға болады:
және осыны пайдаланып дифференциалдың формуласын былай жазуға болады:
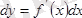 . Осыдан
. Осыдан
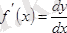 , яғни туынды функцияның дифференциалының аргумент дифференциалына бөлінген мәніне тең.
, яғни туынды функцияның дифференциалының аргумент дифференциалына бөлінген мәніне тең.
Дифференциалды есептеу ережесі.
Айталық
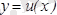 және
және
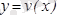 дифференциалданатын функциялар болсын,
дифференциалданатын функциялар болсын,
1)
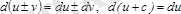 , мұндағы
с -
сан.
, мұндағы
с -
сан.
2)
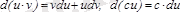 ,
,
3)
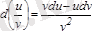 , егер
, егер
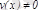 .
.
4) Егер
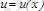 функциясы
функциясы
 нүктесінде дифференциалданатын, ал
нүктесінде дифференциалданатын, ал
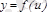
 нүктесінде дифференциалданатын болса, онда
нүктесінде дифференциалданатын болса, онда
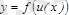 күрделі функция үшін,
күрделі функция үшін,
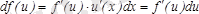 . Бұл ережені
бірінші дифференциал формасының инварианттығы
деп атайды. Дифференциалды жуықтап есептеуге қолдануға болады. Айталық,
. Бұл ережені
бірінші дифференциал формасының инварианттығы
деп атайды. Дифференциалды жуықтап есептеуге қолдануға болады. Айталық,
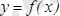 функциясы дифференциалданатын болсын, онда оның өсімшесі:
функциясы дифференциалданатын болсын, онда оның өсімшесі:
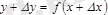 , осыдан
, осыдан
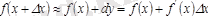 .
.
Егер
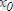 нүктесінде функцияның мәні берілсе, онда:
нүктесінде функцияның мәні берілсе, онда:
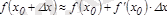
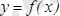 функциясы
функциясы
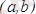 аралығында берілсін. Егер кез келген
аралығында берілсін. Егер кез келген
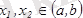 үшін
үшін
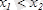 теңсіздігінен
теңсіздігінен
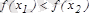 (
(
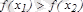 ) теңсіздігі шығатын болса, онда
) теңсіздігі шығатын болса, онда
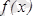 функциясы
функциясы
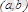 аралығында өседі (кемиді) дейді.
аралығында өседі (кемиді) дейді.
Теорема.
Егер
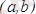 аралығында дифференциалданатын
аралығында дифференциалданатын
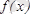 функция-сының туындысы осы аралықта оң (теріс) болса, онда ол осы аралықта өседі (кемиді) . Демек, өсу немесе кему интервалында функцияның туындысы таңбасын өзгертпейді.
функция-сының туындысы осы аралықта оң (теріс) болса, онда ол осы аралықта өседі (кемиді) . Демек, өсу немесе кему интервалында функцияның туындысы таңбасын өзгертпейді.
1-мысал
.
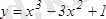 функцияның өсу және кему аралықтарын табу керек. Ол үшін функция туындысының таңбасының тұрақтылық интервалдарын анықтаймыз
функцияның өсу және кему аралықтарын табу керек. Ол үшін функция туындысының таңбасының тұрақтылық интервалдарын анықтаймыз
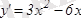 . Бұл квадрат үшмүшеліктің түбірлері
x
1
=0, x
2
=2.
Сондықтан, егер
. Бұл квадрат үшмүшеліктің түбірлері
x
1
=0, x
2
=2.
Сондықтан, егер
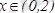 аралығында
аралығында
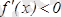 , демек
, демек
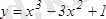 функциясы бұл аралықта кемиді. Ал
функциясы бұл аралықта кемиді. Ал
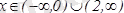 аралықтарында
f'(x) >0,
демек бұл аралықтарда функция өседі.
аралықтарында
f'(x) >0,
демек бұл аралықтарда функция өседі.
Теорема (экстремумның қажетті шарты) .
Егер дифференциалданатын
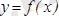 функциясының
функциясының
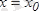 нүктесінде экстремумы бар болса, онда сол нүктеде
нүктесінде экстремумы бар болса, онда сол нүктеде
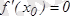 болады. Осы теоремадан мынадай қорытындыға келеміз: егер
болады. Осы теоремадан мынадай қорытындыға келеміз: егер
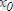 нүктесінде функцияның экстремумы бар болса, онда ол нүктеде оның туындысы нөлге тең, не ол нүктеде туындысы болмауы мүмкін. Кері тұжырым әрқашан орындала бермейді.
нүктесінде функцияның экстремумы бар болса, онда ол нүктеде оның туындысы нөлге тең, не ол нүктеде туындысы болмауы мүмкін. Кері тұжырым әрқашан орындала бермейді.
Мысалы,
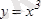 функциясының
x
0
=0
нүктесінде туындысы
функциясының
x
0
=0
нүктесінде туындысы
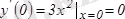 , ал бірақ ол нүктеде функция не максимум, не минимум қабылдамайды.
, ал бірақ ол нүктеде функция не максимум, не минимум қабылдамайды.
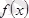 функциясының туындысы нөлге айналатын немесе тіпті болмайтын нүктелерді күдікті нүктелер немесе «кризистік» нүктелер деп атайды. Функцияның экстремумын осы күдікті нүктелердің арасынан іздеу керек.
функциясының туындысы нөлге айналатын немесе тіпті болмайтын нүктелерді күдікті нүктелер немесе «кризистік» нүктелер деп атайды. Функцияның экстремумын осы күдікті нүктелердің арасынан іздеу керек.
Теорема(экстремум бар болуының жеткілікті шарты) .
Егер
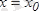 нүктесінде
нүктесінде
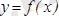 функциясының туындысы нөлге тең болса және
функциясының туындысы нөлге тең болса және
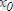 нүктесінен өткенде
нүктесінен өткенде
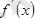 таңбасын өзгертсе, онда
таңбасын өзгертсе, онда
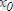 нүктесі экстремум нүктесі болады: 1) егер таңба «плюс»-тен «минус»-ке өзгерсе, онда
нүктесі экстремум нүктесі болады: 1) егер таңба «плюс»-тен «минус»-ке өзгерсе, онда
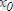 - максимум нүктесі; 2) егер таңба «минус»-тен «плюс»-ке өзгерсе, онда
- максимум нүктесі; 2) егер таңба «минус»-тен «плюс»-ке өзгерсе, онда
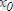 - минимум нүктесі болады.
- минимум нүктесі болады.
2-мысал.
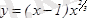 функцияны экстремумге зерттеп, өсу және кему аралықтарын анықтау керек. Функция туындысы
функцияны экстремумге зерттеп, өсу және кему аралықтарын анықтау керек. Функция туындысы
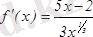 , осыдан
, осыдан
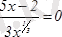 ,
,
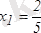 күдікті нүктесін табамыз.
күдікті нүктесін табамыз.
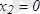 нүктесінде функцияның туындысы болмайды, сондықтан ол да күдікті нүкте. Интервалдар тәсілімен
f '(x) -
тің таңбаларын анықтаймыз. Функция
нүктесінде функцияның туындысы болмайды, сондықтан ол да күдікті нүкте. Интервалдар тәсілімен
f '(x) -
тің таңбаларын анықтаймыз. Функция
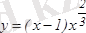 барлық нүктелерде үзіліссіз, жеткіліктілік шарт бойынша
барлық нүктелерде үзіліссіз, жеткіліктілік шарт бойынша
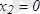 максимум нүктесі, ал
максимум нүктесі, ал
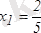 минимум нүктесі. (-¥, 0) және
минимум нүктесі. (-¥, 0) және
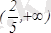 интервалдарда функция өседі, ал
интервалдарда функция өседі, ал
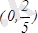 интервалда кемиді Зерттеу нәтижелерін таблицаға жазамыз:
интервалда кемиді Зерттеу нәтижелерін таблицаға жазамыз:
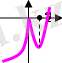
Функцияның екінші ретті туындысы қолданылатын экстремумның тағы бір шартын келтірейік.
Теорема.
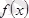 функциясының
функциясының
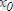 нүктесінде бірінші және екінші туындылары бар болсын. Егер
нүктесінде бірінші және екінші туындылары бар болсын. Егер
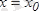 нүктесінде
нүктесінде

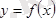 функциясының бірінші туындысы нөлге тең, яғни
функциясының бірінші туындысы нөлге тең, яғни
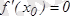 болса, ал екінші туындысы нөлден ерекше, яғни
болса, ал екінші туындысы нөлден ерекше, яғни
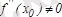 болса, онда
болса, онда
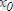 - экстремум нүктесі болады:
- экстремум нүктесі болады:
1) егер
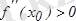 болса, онда
болса, онда
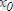 - минимум нүктесі;
- минимум нүктесі;
2) егер
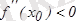 болса, онда
болса, онда
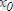 - максимум нүктесі болады.
- максимум нүктесі болады.
Функцияның кесіндідегі ең үлкен және ең кіші мәндері . Функция өзінің ең үлкен және ең кіші мәндерін экстремум нүктелерінде не кесіндісінің шеткі нүктелерінде қабылдауы мүмкін. Ең үлкен және ең кіші мәндерді табу үшін алдымен функцияның күдікті нүктелерін (не туынды нөлге тең, не туынды жоқ нүктелер) табу керек. Содан соң функцияның күдікті нүктелеріндегі және кесіндінің шеткі нүктелеріндегі мәндерін тауып, олардың ішінен ең үлкен және ең кіші мәндерді іздеу керек.
3-мысал.
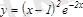 функциясының
функциясының
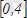 кесіндісіндегі ең үлкен жіне ең кіші мәндерін табу керек. Күдікті нүктелерді табамыз:
кесіндісіндегі ең үлкен жіне ең кіші мәндерін табу керек. Күдікті нүктелерді табамыз:
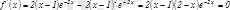
Осыдан
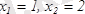 - күдіктінүктелер. :
- күдіктінүктелер. :
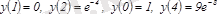 .
.
Сонымен
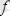 үлкен
үлкен
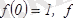 кіші
кіші
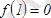 .
.
Анықтама.
Егер
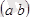
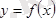 қи-, (дөңестігітөменқараған) дейді, ал
қи-, (дөңестігітөменқараған) дейді, ал
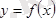 , () дейді. Қисықтың ойыс және дөңес бөлігін бөліп тұратын нүктені
иілу нүктесі
деп атайды.
, () дейді. Қисықтың ойыс және дөңес бөлігін бөліп тұратын нүктені
иілу нүктесі
деп атайды.
Теорема.
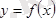 функциясы
функциясы
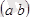 интервалында екі рет дифференциал-данатын болсын. Егер осы интервалдың әрбір нүктесінде 1)
интервалында екі рет дифференциал-данатын болсын. Егер осы интервалдың әрбір нүктесінде 1)
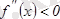 болса, онда функцияның графигі бұл интервалда дөңес болады; 2)
болса, онда функцияның графигі бұл интервалда дөңес болады; 2)
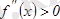 болса, онда функцияның графигі бұл интервалда ойыс болады
болса, онда функцияның графигі бұл интервалда ойыс болады
4-мысал.
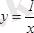 гиперболасы (0, +¥) интервалында ойыс болады, себебі
гиперболасы (0, +¥) интервалында ойыс болады, себебі
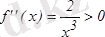 , ал (-¥, 0) интервалында дөңес, себебі
, ал (-¥, 0) интервалында дөңес, себебі
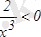 .
.
Теорема (иілу нүктесінің қажетті шарты) .
Егер
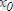 нүктесі
нүктесі
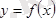 функциясының иілу нүктесі болса, онда бұл нүктеде функцияның екінші туындысы нөлге тең, яғни
функциясының иілу нүктесі болса, онда бұл нүктеде функцияның екінші туындысы нөлге тең, яғни
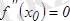 . Функцияның екінші туындысы нөлге айналатын немесе екінші туындысы болмайтын нүктелер екінші текті күдікті нүктелер деп аталады. Функцияның иілу нүктесін осы күдікті нүктелердің арасынан іздеу керек.
. Функцияның екінші туындысы нөлге айналатын немесе екінші туындысы болмайтын нүктелер екінші текті күдікті нүктелер деп аталады. Функцияның иілу нүктесін осы күдікті нүктелердің арасынан іздеу керек.
Теорема (иілу нүктенің жеткілікті шарты) .
Егер
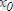 нүктесінен өткенде функцияның екінші туындысы таңбасын өзгертсе, онда
нүктесінен өткенде функцияның екінші туындысы таңбасын өзгертсе, онда
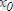 нүктесі иілу нүктесі болады.
нүктесі иілу нүктесі болады.
1. 2 Алғашқы функция және анықталмаған интеграл, оның негізгі қасиеттері мен есептеу әдістері [5] -[9]
Интеграл ұғымы жазық фигураның ауданын, сондай-ақ дененің беті ауданын және көлемін есептеу қажеттілігінен пайда болды. Мәселен, Ежелгі Греция мен Римде математик ғалымдар кез келген жазық фигураның квадратурасын және кез келген дененің кубатурасын табуға есептер шығарумен айналысқан. Олар өз есептеулерінде Книдский Евдокс ұсынған біртіндеп түгесу әдісін [9] қолданған. Мысалы, бұл әдісті қолдану арқылы Евдокс екі дөңгелектің аудандарының қатынасы олардың диаметрлері квадраттарының қатынасына, ал табаны мен биіктігі цилиндрдікіндей болатын конустың көлемі цилиндр көлемінің
 бөлігіне тең екені дәлелденген.
бөлігіне тең екені дәлелденген.
Архимед өзінің «парабола квадратусы» шығармасында Евдокс әдісін жетілдіріп, дөңгелектің ауданын есептеу формуласын қорытып шығарды. Архимед әдісінің негізгі мағынасы мынада: алдымен дөңгелектің ауданы оған сырттай сызылған кез келген дұрыс көпбұрыштың ауданынан кіші, бірақ оған іштей сызылған кез-келген дұрыс көпбұрыштың ауданынан үлкен екені дәлелденеді. Содан кейін іштей және сырттай сызылған дұрыс көпбұрыштардың қабырғалар санын екі еселеп арттырғанда олардың аудандарының айырымы өте аз шама болатыны дәлелденеді.
Ең соңында сырттай сызылған дұрыс көпбұрыштың қабырғалар санын шексіз екі еселеп арттырғанда оның ауданының ұмтылатын сандық шамасы дөңгелек ауданының шамасы ретінде табылады.
«
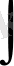 » интеграл белгісін Г. В. Лейбниц 1675ж. енгізген [9] . Бұл белгі «summa» сөзіндегі S латын әрпінің өзгерген алғашқы күйі, қалпына келтіру ұғымын білдіретін «integro» деген латын сөзінен шыққан. Мұның тұтас деген мағына беретін «integer» сөзінен шығуы да мүмкін.
» интеграл белгісін Г. В. Лейбниц 1675ж. енгізген [9] . Бұл белгі «summa» сөзіндегі S латын әрпінің өзгерген алғашқы күйі, қалпына келтіру ұғымын білдіретін «integro» деген латын сөзінен шыққан. Мұның тұтас деген мағына беретін «integer» сөзінен шығуы да мүмкін.
Анықтама: Х жиынында өзгеретін кез келген х үшін:
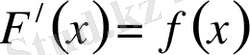

теңдігі орындалса, онда
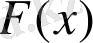 функциясы осы жиында
функциясы осы жиында
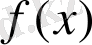 функциясының алғашқы функциясы деп аталады.
функциясының алғашқы функциясы деп аталады.
Мысалы: Алғашқы функцияның анықтамасы бойынша
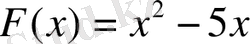 функциясының тундысын табамыз:
функциясының тундысын табамыз:
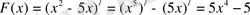
Демек, кез келген
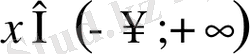 үшін
үшін
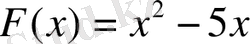 функциясы
функциясы
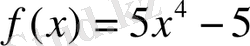 функциясының алғашқы функциясы болады.
функциясының алғашқы функциясы болады.
Берілген функцияның туындысын табу дифференциалдау деп аталатыны математика курсынан белгілі. Ал функцияның белгілі туындысы бойынша алғашқы функциясын анықтауды интегралдау деп атаймыз.
Интегралдау амалы дифференциалдау амалына кері амал. Интегралдаудың негізгі мақсаты интегралданатын функцияның барлық алғашқы функцияларын табу. Мысалы:
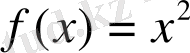 функциясының алғашқы функциясы ретінде
функциясының алғашқы функциясы ретінде
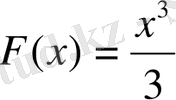 функциясын ғана емес,
функциясын ғана емес,
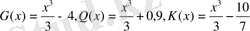 және т. с. с. функияларды алуға болады. Себебі, бұл алғашқы функциялардың туындысын анықтасақ, барлық жағдайда да
және т. с. с. функияларды алуға болады. Себебі, бұл алғашқы функциялардың туындысын анықтасақ, барлық жағдайда да
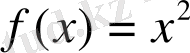 функциясына келеміз. Олай болса, кез келген
функциясына келеміз. Олай болса, кез келген
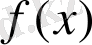 функциясы үшін бір алғашқы функция табылса, онда оның шексіз көп алғашқы функциялары бар болады.
функциясы үшін бір алғашқы функция табылса, онда оның шексіз көп алғашқы функциялары бар болады.
Теорема: Егер
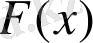 функциясы Х аралығында
функциясы Х аралығында
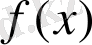 функциясының алғашқы функциялрының бірі болса, онда бұл функцияның барлық алғашқы функцияларының жиыны
функциясының алғашқы функциялрының бірі болса, онда бұл функцияның барлық алғашқы функцияларының жиыны
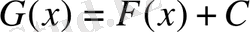

формуласымен анықталады. Мұндағы С-кез келген тұрақты сан.
Анықтама:
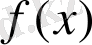 функциясының алғашқы функцияларының жалпы түрін, яғни
функциясының алғашқы функцияларының жалпы түрін, яғни
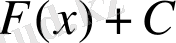 өрнегін осы функцияның анықалмаған интегралы деп атайды.
өрнегін осы функцияның анықалмаған интегралы деп атайды.
Анықталмаған интегралды табу формуласы:
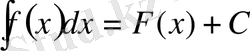

 формуладағы
формуладағы
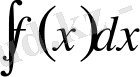 -анықталмаған интеграл.
-анықталмаған интеграл.
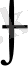 интегралдау амалының белгісі.
интегралдау амалының белгісі.
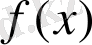 - интеграл таңбасы астындағы функция,
- интеграл таңбасы астындағы функция,
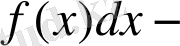 интеграл таңбасы астындағы өрнек.
интеграл таңбасы астындағы өрнек.
1. 1-мысал:
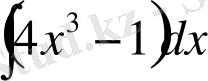 интегралын табайық.
интегралын табайық.
Шешуі:
 формула мен алғашқы функцияны табу кестесін қолданамыз. Сонда
формула мен алғашқы функцияны табу кестесін қолданамыз. Сонда
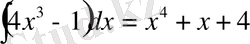 болады.
болады.
Анықталмаған итегралдың қарапайым қасиеттері
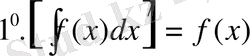
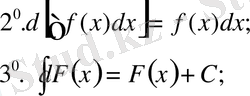
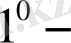 қасиет
қасиет
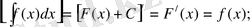 теңдіктері арқылы дәлелденеді, яғни анықталмаған интегралдың туындысы интеграл астындағы функцияға тең.
теңдіктері арқылы дәлелденеді, яғни анықталмаған интегралдың туындысы интеграл астындағы функцияға тең.
 қасиет
қасиет
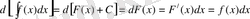 теңдіктері көмегімен дәлелденеді, яғни дифференциял таңбасы интеграл таңбасынан бұрын тұрса, онда
теңдіктері көмегімен дәлелденеді, яғни дифференциял таңбасы интеграл таңбасынан бұрын тұрса, онда
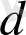 мен
мен
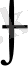 таңбалары өзара жойылып кетеді.
таңбалары өзара жойылып кетеді.
 қасиет
қасиет
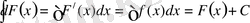 теңдіктері арқылы дәелденеді, яғни, егер дифференциал және интеграл таңбаларының орындарын алмастырып, оларды қысқартсақ, онда ол таңбалардың өзара жойылуы кез келген тұрақты С санына дейінгі дәлдікпен орындалады.
теңдіктері арқылы дәелденеді, яғни, егер дифференциал және интеграл таңбаларының орындарын алмастырып, оларды қысқартсақ, онда ол таңбалардың өзара жойылуы кез келген тұрақты С санына дейінгі дәлдікпен орындалады.
 Егер
Егер
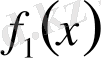 және
және
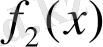 функцияларының Х аралығында алғашқы функциялары бар болса, онда сол аралықта
функцияларының Х аралығында алғашқы функциялары бар болса, онда сол аралықта
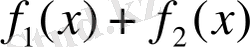 функиясының да алғашқы функциясы бар болады және
функиясының да алғашқы функциясы бар болады және
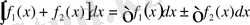

теңдігі орындалады.
Шынында да,
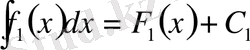 және
және
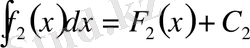 дейік. Олай болса,
дейік. Олай болса,
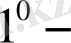 қасиет бойынша
қасиет бойынша
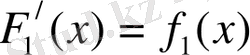 және
және
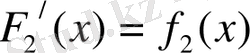 .
.
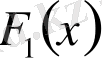 және
және
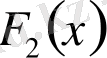 функциялары қосындысын (айырмасын)
функциялары қосындысын (айырмасын)
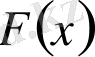 арқылы белгілейік. Сонда Х аралығында
арқылы белгілейік. Сонда Х аралығында
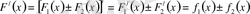
теңдігі орындалады. Ал бұл теңдік
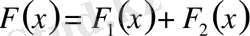 функциясы
функциясы
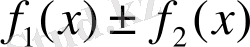 функциясының алғашқы функциясы екенін көрсетеді. Сондықтан
функциясының алғашқы функциясы екенін көрсетеді. Сондықтан
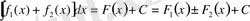
Демек,
 формуланың сол жағы
формуланың сол жағы
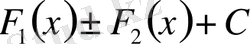 өрнегімен, ал оң жағы
өрнегімен, ал оң жағы
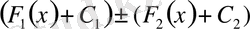 қосындысынан (айырмасынан) тұрады. Бірақ,
қосындысынан (айырмасынан) тұрады. Бірақ,
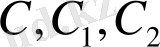 тұрақтылары кез келген еркімізше алынған сандар болғандықтан,
тұрақтылары кез келген еркімізше алынған сандар болғандықтан,
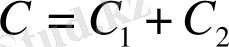 деп жазуға болады, яғни
деп жазуға болады, яғни
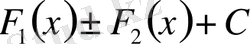 және
және
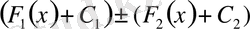 жиындары бір біріне тең.
жиындары бір біріне тең.
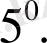 Егер
Егер
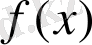 -тің Х аралығында алғашқы функциясы бар болса, онда кез келген
-тің Х аралығында алғашқы функциясы бар болса, онда кез келген
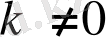 саны үшін
саны үшін
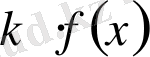 функциясының сол аралықта алғашқы функциясы бар болып және мына теңдік орындалады:
функциясының сол аралықта алғашқы функциясы бар болып және мына теңдік орындалады:
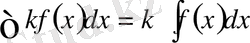
Шынында да,
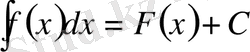 дейік. Олай болса,
дейік. Олай болса,
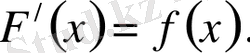 Х аралығында
Х аралығында
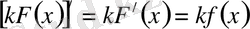 болғандықтан,
болғандықтан,
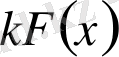 функциясы
функциясы
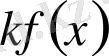 функциясының сол аралықтағы алғашқы функциясы. Сондықтан
функциясының сол аралықтағы алғашқы функциясы. Сондықтан
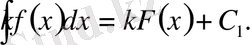 Ал теңдіктің оң жағы
Ал теңдіктің оң жағы
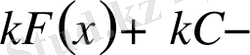 ға тең. Олай болса,
ға тең. Олай болса,
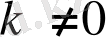 үшін
үшін
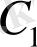 және
және
 сандары еркінше алынған тұрақты сандар болғандықтан,
сандары еркінше алынған тұрақты сандар болғандықтан,
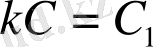 болады.
болады.
Анықталмаған интегралдың
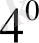 және
және
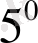 қасиеттері оның қасиеттері деп аталады. Бұларды біріншісі функциялар қосындысының анықталмаған интегралы сол функциялардан жеке-жеке алынған анықталмаған интегралдар қосындысына тең екенін көрсетеді, ал екіншісі тұрақты көбейткішті интеграл алдына шығаруға болатынын көрсетеді.
қасиеттері оның қасиеттері деп аталады. Бұларды біріншісі функциялар қосындысының анықталмаған интегралы сол функциялардан жеке-жеке алынған анықталмаған интегралдар қосындысына тең екенін көрсетеді, ал екіншісі тұрақты көбейткішті интеграл алдына шығаруға болатынын көрсетеді.
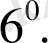 Еер Х аралығында
Еер Х аралығында
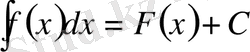 болса, онда сол аралықта
болса, онда сол аралықта
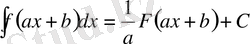
Шынында да,
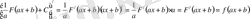
Интегралдаудың негізгі әдістері
1. Айнымалыны ауыстыру жолымен интегралдау (ауыстыру әдісі) . Кестелік интегралдарға жатпайтын көптеген интегралдар астындағы функциялардың алғашқы функцияларын бірден табу көбіне қиындыққа түседі. Мұндай интегралдарды есептеудің ең тиімді әдістерінің бірі айнымалыны ауыстыру әдісі болып табылады. Ауыстыру әдісін қолдану интегралдарды қарапайым (көбіне кестелік) интегралдарға түрлендірейік. Бұл әдіс мынадай теоремаға негізделген:
Теорема: Егер кейбір Т аралығында үзіліссіз
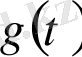 функциясы
функциясы
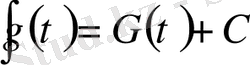 теңдігін қанағаттандыратын болса, онда Х аралығында үзіліссіз дифференциялданатын ( яғни туыдысы да үзіліссіз )
теңдігін қанағаттандыратын болса, онда Х аралығында үзіліссіз дифференциялданатын ( яғни туыдысы да үзіліссіз )
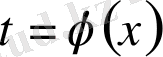 функциясы
функциясы
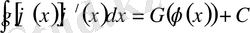 теңдігін қанағаттандырады (мұндағы Т аралығы
теңдігін қанағаттандырады (мұндағы Т аралығы
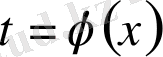 функциясының өзгеру облысы) .
функциясының өзгеру облысы) .
Дәлелдеуі: Теореманы дәлелдеу үшін мына байланысты келтіреміз:
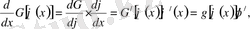
мұндағы
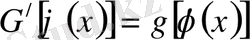 . Бұдан теоремадағы теңдіктің дәлелдемесі тікелей шығады.
. Бұдан теоремадағы теңдіктің дәлелдемесі тікелей шығады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz