Электротехника негіздері: тұрақты ток тізбектері, тізбек элементтері және Кирхгоф заңдары


Қазақстан Республикасының Білім және ғылым министрлігі
Е. А. Бөкетов атындағы Қарағанды мемлекеттік Университеті
Е. А. Бөкетов атындағы Қарағанды мемлекеттік Университетінің коледжі
Алпысова Г. К.,
оқытушы
«Электротехника негіздері»
пәні бойынша
ДӘРІС КУРСЫ
Мамандық: «Тасымалдауды ұйымдастыру және көлік қозғалысын басқару (салалар бойынша) »
Қарағанды
2012
- тақырып Тұрақты ток электр тізбегіЭлектр тізбектері және оның бөліктеріЭлектр тізбегінің элементтері. Тізбек элементтерінің параметрлері.
1. 3 Тізбек элементтерінің номинал, бос жүріс және қысқа тұйықталу әлпілерінің түсініктері
1. 4 Кирхгофтың бірінші заңы
1. 5 Кирхгофтың екінші заңы
1. 6 Кирхгоф заңдарын тізбектерде есептерде қолдану
1. 7 Тізбектерді баламалы түрлендіру
- Электр тізбектері және оның бөліктері
Электрлендіру өнеркәсібінің электр энергиясын оның көзінен электр қабылдағышарға жеткізу, тарату және басқару үшін әр түрлі қондырғылар мен құрылғыларды сым арқылы бірімен - бірін қосып электр тізбегін құрастырады.
Электр тізбегі деп электрлік үрдістері электр қозғаушы күш (ЭҚК), ток және кернеу ұғымдарымен түсіндірілетін, электр тогы жүретін жол түзетін ұондырғылар мен құрылғылардың жиынтығын айтады. Электр тізбегі үлкен үш бөліктен тұрады: электр энергиясы көздерінен, электр энергиясын тасымалдайтын, тарататын һәм оны басқаратын қондырғылар мен құрылғылардан және электр қабылдағыштардан.
Электр энергиясының көзі деп басқа бір энергияны электр энегиясына түрлендіруге арналған қондырғыны немесе аспапты айтады. Мысалы, аккумулятор, электр генераторы (машина), термоэлектр генераторы, фотоэлемент т. б.
Электр энергиясын тасымалдайтын, тарататын құрылғылар мен қондырғыларға және басқаратын аспаптарға электр желілері, трансформаторлар, ажыратқыштар, сақтандырғыштар, релелер т. с. с жатады.
Электрлік қабылдағыш деп, әдетте, электр энергиясын басқа энергияға түрлендіруге арналған қондырғыны, құрылғыны немесе аспапты айтады. Мысалы, электрлік қоздырғыштарда электр энергиясы негізінен механикалық энергияға түрленсе, электролиз астауларында химиялық реакцияның энергиясына түрленеді.
Электр тізбектерін әр түрлі мақсаттағы жұмыстарды орындау үшін графикалық түрде кескіндейді. Электр тізбегінің шартты белгілер арқылы келтірілген графикалық кескіні электрлік сұлба деп аталады. (1. 1- сурет)
Электрлік сұлбалар мақсатына қарай монтаждық, функциялық, парқылық, орынбасарлық т. с. с болып бөлінеді. Шартты белгілердің графикалық кескінін және мөлшерін халықаралық шартты белгілерге сәйкестендіре отырып Мемлекеттік Стандарт (МСт) қабылдаған. Сондықтан олардың кескінін және мөлшерін бұрмалауға болмайды.

1. 1-сурет Электр тізбегінің сұлбасы мен (а) мен тізбек элементтердің шартты белгілері (б) : 1- электр энергиясының көзі; 2- екі полюсті ажыратқыш; 3- сақтандырғыш; 4- электр қабылдағыш.
Электр тізбегіндегі әрбір қондырғы, құрылғы немесе аспап тізбектің элементі деп аталады. Тізбек элементтерін шартты графикалық белгілермен қатар, шартты әріптермен белгілеу де қабылданған. Мысалы электр энергиясын
 әрпімен белгілеу қабылданған, ал графикалық белгілеудегі тілсызық (стрелка) әрқашанда қорек көзінің потенциалы жоғары нүктесін көрсетіп тұруы керек.
әрпімен белгілеу қабылданған, ал графикалық белгілеудегі тілсызық (стрелка) әрқашанда қорек көзінің потенциалы жоғары нүктесін көрсетіп тұруы керек.
Тізбектің бір ток жүретін бөлігі тармақ деп аталады. Қарастырылып отырған тізбекте үш тармақ бар:
 және
және
 .
.
Үш не одан да көп тармақтардың қосылған нүктесі түйін деп аталады (суретте а және с) . Электрлік сұлбада түйінді нүкте қойып белгілейді. Егер нүкте қойылмаса, онда сымдар электрлік байланыспаған, айқасып қана жатыр деп есептелінеді.
Тізбектің ток жүретін кез- келген бөлігі өнбой (контур) деп аталады. Келтірілген тізбекте үш контур бар:
 және сыртқы контур
және сыртқы контур
 . Ең болмаса бір тармағы бойынша ерекшеленетін контурларды өзара тәуелсіз контурлар деп атайды.
. Ең болмаса бір тармағы бойынша ерекшеленетін контурларды өзара тәуелсіз контурлар деп атайды.
Электр тізбегінде элементтер тіркес (бірізді), паралель және аралас түрде жалғанады. Егер тізбек элементтері олармен бір ток өтетіндей етіп, яғни бірінің аяғы екіншінің басымен, екіншінің аяғы үшіншінің басымен т. с. с жалғанса онда мұндай жалғануды тіркес жалғау деп атайды. Суретте
 мен
мен
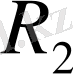 электр қабылдағыштары тіркес, ал
электр қабылдағыштары тіркес, ал
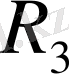 пен
пен
 электр қабылдағыштары параллель жалғанған. Егер тізбекте элементтер тіркес пен параллель жалғанған болса, онда мұндай жалғау аралас жалғау деп аталады. Қарастырылып отырған тізбекте тізбек элементтері аралас жалғанған.
электр қабылдағыштары параллель жалғанған. Егер тізбекте элементтер тіркес пен параллель жалғанған болса, онда мұндай жалғау аралас жалғау деп аталады. Қарастырылып отырған тізбекте тізбек элементтері аралас жалғанған.
1. 2 Электр тізбегінің элементтері
Ток жоқ кезде қысқыштарында кернеуі бар элемент активті, ал ток жоқ кезде кернеуі жоқ элемент пассивті элемент деп аталады. Қорек көздері активті де, ал электр қабылдағыштар пассивті болып табылады.
Әрбір пассивті элементтің кернеуі, тогы және кедергісі Ом заңы бойынша байланысқан:

Мұндағы,
 -- кернеу;
-- кернеу;
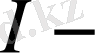 ток күші;
ток күші;
 - кедергі.
- кедергі.
Тізбек элементінің кернеуі деп оның басы мен аяғының арасындағы потенциалдар айырымын айтады. Оны, яғни
 көбейтіндісін, кернеудің түсуі деп те атайды. Пассивті элементте кернеу мен ток әрқашанда бағыттас болады: олар потенциалы жоғары нүктеден потенциалы төмен нүктеге бағытталады. Мысалы,
көбейтіндісін, кернеудің түсуі деп те атайды. Пассивті элементте кернеу мен ток әрқашанда бағыттас болады: олар потенциалы жоғары нүктеден потенциалы төмен нүктеге бағытталады. Мысалы,
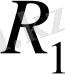 элементінің кернеуі (1. 1-сурет)
элементінің кернеуі (1. 1-сурет)
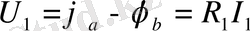 ,
,
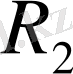 элементінің кернеуі
элементінің кернеуі
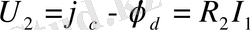 .
.
 элементі мен
элементі мен
 элементі параллель жалғанғандықтан кернеулері өзара тең болады, яғни
элементі параллель жалғанғандықтан кернеулері өзара тең болады, яғни
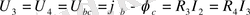
Потенциалдар айырымы, яғни кернеу, өткізгіште ток тудырады:
 . Потенциалы бірдей нүктелердің арасында кернеу болмайды, сондықтан ток жүрмейді.
. Потенциалы бірдей нүктелердің арасында кернеу болмайды, сондықтан ток жүрмейді.

Элементтің кернеуінің тогынан тәуелділігін оның вольт- амперлік сипаттамасы деп атайды. Әдетте элементтің тогы өскен сайын кернеуі де өсіп отырады. Бірақ осы байланысты көрсететін график - вольт -амперлік сипаттама, түзу сызық немесе қисық сызық болуы (1. 2- сурет) . Бұл элементтің кедергісіне байланысты: егер элементтің кедергісі тұрақты болса, онда вольт- амперлік сипаттама түзу сызық та, ал элементтің кедергісі токтың әсерінен өзгеріп отырса, онда вольт -амперлік сипаттама қисық сызық болады. Вольт- амперлік сипаттамасы түзу сызық болатын элементтер сызықты, ал қисық сызық болатын элементтер бейсызықты (түзу сызықты емес) элементтер деп аталады.
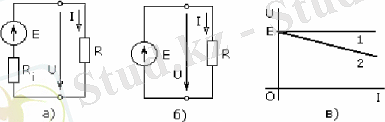
1. 3- сурет Реал (а) және идеал (б) ЭҚК көздерінің электрлік сұлбалары мен вольт -амперлік сипаттамалары: 1- идеал ЭҚК көзі; 2- реал ЭҚК көзі
Электр қозғаушы күші және ішкі кедергісі бар электр энергиясының көзі электр қозғаушы күш көзі деп аталады (1. 3, а- сурет) . Егер ЭҚК көзіне электр қабылдағыш қосса, онда тізбекпен жүретін ток
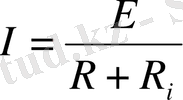
Бұдан
 , (1. 1)
, (1. 1)
мұндағы:
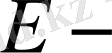 электр қозғаушы күш;
электр қозғаушы күш;
 электр қабылдағыштың кедергісі;
электр қабылдағыштың кедергісі;
 ЭҚК көзінің ішкі кедергісі.
ЭҚК көзінің ішкі кедергісі.
(1. 1 ) өрнегінен ЭҚК көзінің кернеуі
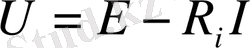 .
.
Бұл өрнек ЭҚК көзінің тогы, яғни жүгі өскен кезде, ішкі кедергідегі кернеудің түсуінің өсетіні себепті, кернеуінің азаятындығын көрсетеді (1. 3, в- сурет, 2- вольт -амперлік сипаттама) . Ал кернеудің төмендеуі электр қабылдағыштың жұмыс әлпіне жағымсыз әсер етеді. Сондықтан ЭҚК көзінің ішкі кедергісі электр қабылдағыштың кедергісінен әлдеқайда аз болатындай етіп жасалады, яғни
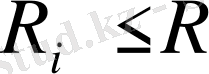 болады.
болады.
Ішкі кедергісі нөлге тең деп алынған ЭҚК көзі идеал ЭҚК көзң немесе кернеу көзі деп аталады (1. 3, б- сурет) . Идеал ЭҚК көзінің кернеуі токтан, яғни жүктен, тәуелсіз және тұрақты деп есептелінеді, өйткені
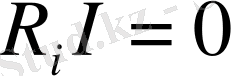 , сондықтан
, сондықтан
 (1. 3, в- сурет, 1- вольт -амперлік сипаттама) .
(1. 3, в- сурет, 1- вольт -амперлік сипаттама) .
ЭҚК көзінде ұйықтар (зарядтар) бөгде күштің әсерінен потенциалы төмен нүктеден потенциалы жоғары нүктеге тасымалданатындықтан әдетте ЭҚК пен ток бағыттас болады. Бірақ ЭҚК көзі электр қабылдағыш әлпінде істеп тұрса, яғни энергия берудің орнына энергия қабылдап тұрса (мысалы, зарядтауға қойылған аккумулятор), онда ток ЭҚК көзіне қарсы бағытталады. ЭҚК потенциалдар айырымын тудыратын элемент болғандықтан, оның ЭҚК-і ток тудырушы себеп болып табылады, яғни ЭҚК ток тударады:
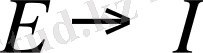
Егер (1. 1) өрнектің екі жағын да токқа көбейтсе, онда тізбек элементтерінің қуаттарының ара қатынасын көрсететін теңдік шығады:
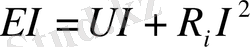 немесе
немесе
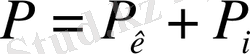 , (1. 2)
, (1. 2)
Мұндағы:
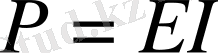 - ЭҚК көзінің тізбекке берген қуаты;
- ЭҚК көзінің тізбекке берген қуаты;
 - электр қабылдағыштың қуаты;
- электр қабылдағыштың қуаты;
 ЭҚК көзінің ішкі кедергісіндегі қуат, басқаша айтқанда қуаттың шығыны.
ЭҚК көзінің ішкі кедергісіндегі қуат, басқаша айтқанда қуаттың шығыны.
Электр қозғаушы күш көзінің тізбекке берген қуаты мен электр қабылдағыштарының тұтынған қуатының өзара тең болатындығын өрнектейтін теңдеуді қуаттар балансының теңдеуі деп атайды. (1. 2) өрнегі 1. 3, а- суретте келтірілген тізбектегі қуаттар баланысының теңдеуі болып табылады.
Тізбек элементтерінің параметрлері. Орынбасарлық сұлба туралы түсінік.
Тізбекпен ток жүрген кезде электр энергиясы басқа энергия түрлеріне айналып отырады. Мысалы, сымның бойымен ток жүргенде сым қызады және оның айналасында магнит һәм электр өрісі пайда болады. Сымды қыздырған электр энергиясы жылу энергиясы түрінде қоршаған ортаға қайтымсыз тарап кетеді. Электр энергиясының екінші бір бөлігі магнит энергиясының бір бөлігіне түрленсе, үшінші бір бөлігі электр өрісінің энергиясына түрленеді. Бірақ сымның қызуы мен магнит өрісі және электр өрісіндегі энергияның шамасы сымның затына һәм мөлшеріне байланысты болады. Олай болса тізбектегі электр энергиясының түрленуі тізбектің және оны құрайтын элементтердің қасиетінен тәуелді. Сондықтан тізбек элементтерінің әр түрлі қасиеттерін сипаттайтын шамалар тізбектің және тізбек элементтерінің параметрлері ретінде алынады.
Тізбек элементінің оған берілген электр энергиясын энергияның басқа түріне қайтымсыз түрлендіретін қасиетін кедергі деп аталатын параметрмен сипаттайды. Кедергінің өлшем бірлігі 1Ом.
Джоуль -Ленц заңына сүйене отырып, тұрақты және айнымалы ток тізбегіндегі тізбек элементінің кедергісін төмендегіше анықтауға болады:
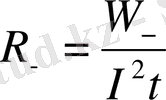 және
және
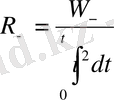
мұндағы:
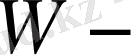 басқа энергияға қайтымсыз түрленген электр энергиясы;
басқа энергияға қайтымсыз түрленген электр энергиясы;
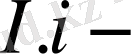 тұрақты және айнымалы ток тізбегіндегі ток күші;
тұрақты және айнымалы ток тізбегіндегі ток күші;
 уақыт.
уақыт.
Тізбек элементінің тұрақты токқа кедергісі омдық кедергі, ал айнымалы токқа кедергісі актив кедергі деп аталады. Жалпы алғанда, омдық және актив кедергілердің сан мәндері өзара тең болмайды. Олардың айырмашылығы жиіліктен тәуелді болады: жиілік өскен кезде айырмашылығы өседі, ал жиілігі азайған кезде айырмашылығы да азаяды. Электрмен жабдықтау жүйесінде қолданылатын 50 не 60 Гц жиілікті ток төмен жиілікті ток болып табылады. Мұндай жиіліктерде омдық кедергі мен активті кедергілердің айырмашылығы өте аз болатындықтан оларды өзара тең деп есептеп, тек кедергі немесе активті кедергі деп атайды.
Негізінен кедергісі бар элементті резистивті элемент деп, ал кедергісін пайдалануға арналған аспапты резистор деп атайды. Мысалы, электр пеші мен шоқтану шамы электр энергиясын жылу энергиясы мен жарық сәулесінің энергиясына қайтымсыз түрлендіретіндіктен резистивті элементтер болып табылады.
Тізбек элементінің оған берілген электр энергиясын магнит өрісінің энергиясына түрлендіретін қасиетін индуктивтілік деп аталатын параметрмен сипаттайды. Индуктивтіліктің өлшем бірлігі 1 Гн (Генри) .
Тізбек элементінің индуктивтілігі магнит ағыны мен оны тудыратын токтың арасындағы пропорционалдық коэффициент ретінде алынатындықтан, тұрақты және айнымалы ток тізбегінде:

Мұндағы
 индуктивтілік қарастырылып отырған өнбоймен (контурмен) ілініскен магнит ағыны.
индуктивтілік қарастырылып отырған өнбоймен (контурмен) ілініскен магнит ағыны.
Индуктивтілігі бар элементті индуктивті элемент деп, ал индуктивтілігін пайдалануға арналған аспапты индуктивтік шарғы (катушка) деп атайды. Мысалы, релелердің шарғылары мен элетр машиналарының келептері (орамдары) индуктивті элементтер, олар магнит өрісін қоздырушы аспап ретінде пайдаланылады.
Тізбек элементінің оған берілген электр энергиясын электр өрісінің энергиясына түрлендіретін қасиетін сыйымдылық деп аталатын параметрмен сипаттайды. Электр сыйымдылықтың өлшем бірлігі 1Ф (фарад) .
Электр сыйымдылық элементінің ұйығы (заряды) мен кернеуінің арасындағы пропорционалдық коэффициент ретінде алынатындықтан, тұрақты және айнымалы ток тізбегінде:
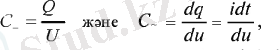
Мұндағы:
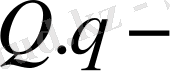 тұрақты және айнымалы ток тізбегінің тізбек элементінің заряды;
тұрақты және айнымалы ток тізбегінің тізбек элементінің заряды;
 тұрақты және айнымалы ток тізбегінің тізбек элементінің кернеуі.
тұрақты және айнымалы ток тізбегінің тізбек элементінің кернеуі.
Электр сыйымдылығы бар элементті сыйымдылықты элемент деп, ал сыйымдылығын пайдалануға арналған аспапты конденсатор деп атайды. Мысалы, жоғары кернеулі кабель және әуе электр желілері сыйымдылықты элементтер ретінде қарастырылады.
Тізбек элементінің параметрлері және оларға сәйкесті аспаптың шартты белгілері 1. 4- суретте келтірілген.

1. 4- сурет Тізбектің идеал элементтері мен олардың шартты белгілері (а, б, в) және екі параметрлі элементтердің орынбасарлық сұлбалары (г, д)
Кез келген тізбек элементінде атлаған үш қасиеттің үшеуі де болады, бірақ бірі әлсіз, екінші бірі күштірек дегендей. Ескерілуге тиісті басым қасиеттеріне қарай тізбектің элементі әдетте бір немесе екі параметрлі болып келеді. Бір параметрі ғана бар, яғни біп ғана қасиеті бар деп алынған элемент идеал немесе идеалданған элемент, ал параметрлері бірден көп, яғни бірнеше қасиеті бар, элемент реал элемент болып есептелінеді. Мыалы, 1. 4- суретте идеал резистивті (а), идеал индуктивті (б) және идеал сыйымдылықты элементтер мен олардың шартты белгілері және активті- индуктивті (г), активті- сыйымдылықты элементтердің (д) орынбасарлық сұлбалары кескінделген.
Тізбектің немесе тізбек элементінің олардың параметрлері арқылы келтірілген графикалық кескінін орынбасарлық сұлба деп атайды. Орынбасарлық сұлба тізбекке әдетте немесе тізбек элементіне талдау жүргізу үшін құрылады. Мысалы, 1. 4, г- суреттегі сұлбаны реал шарғының немесе келептің бірізді орынбасарлық сұлбасы деп есептеуге болады. Жалпы алғанда, тізбек элементі параллель орынбасарлық сұлбамен де кескінделеді.
1. 3 Тізбек элементтерінің номинал, бос жүріс және қысқа тұйықталу әлпілерінің түсініктері
Электрлік қондырғылармен құрылғылар пайдалы әрекет коэффициенті ең жоғарғы және экономикалық тиімді жұмыс әлпін қамтамасыз ететін электрлік және электромеханикалық шамаларға есептеліп жасалады. Қондырғылар мен құрылғылардың паспортында оларды істеп шығарған завод көрсеткен шамалардың мәндерін ноинал мәндер деп атайды. Мысалы, электрлік қозғалтқыштың номинал қуаты
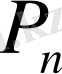 , номинал кернеуі
, номинал кернеуі
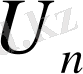 , номинал тогы
, номинал тогы
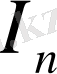 , номинал пайдалы әрекет коэффициенті
, номинал пайдалы әрекет коэффициенті
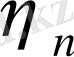 , номинал қуат коэффициенті
, номинал қуат коэффициенті
 , т. с. с деп айтылады. Тізбек элементінің паспорттық мәндеріне сәйкесті жұмыс күйін номинал әлпі деп атайды. Егер элементтің қандай да болмасын бір электрлік шамасы паспорттық мәніне сәйкес келмесе, бұл оның тиімсіз жұмыс істеп тұрғанын көрсетеді. Сонымен, тізбек элементі номинал әлпәнде жұмыс істеуі үшін кернеуі
, т. с. с деп айтылады. Тізбек элементінің паспорттық мәндеріне сәйкесті жұмыс күйін номинал әлпі деп атайды. Егер элементтің қандай да болмасын бір электрлік шамасы паспорттық мәніне сәйкес келмесе, бұл оның тиімсіз жұмыс істеп тұрғанын көрсетеді. Сонымен, тізбек элементі номинал әлпәнде жұмыс істеуі үшін кернеуі
 , тогы
, тогы
 болуы керек.
болуы керек.
Қондырғының немесе құрылғының жүксіз жұмыс күйін бос жүріс әлпі деп атайды. Элементтің бос жүрістік жұмыс күйіндегі шамаларына бос жүріс сөзі қосылып алынады: бос жүріс кернеуі
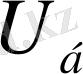 , бос жүріс тогы
, бос жүріс тогы
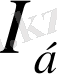 , бос жүріс қуаты
, бос жүріс қуаты
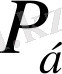 , бос жүрістік пайдалы әсер коэффициенті
, бос жүрістік пайдалы әсер коэффициенті
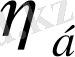 , т. с. с. Бос жүріс әлпінде элементтің кернеуі
, т. с. с. Бос жүріс әлпінде элементтің кернеуі
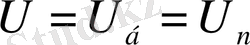 , тогы
, тогы
 , қуаты
, қуаты
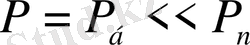 , пайдалы әрекет коэффициенті
, пайдалы әрекет коэффициенті
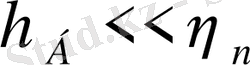 . Бос жүріс әлпіндегі энергияның шығыны салыстырмалы алғанда үлкен болатындықтан пайдалы әрекет коэффициенті өте төмен болады. Сондықтан қондырғының, құрылғының бос жүрісін мүмкіндігінше болдырмау керек.
. Бос жүріс әлпіндегі энергияның шығыны салыстырмалы алғанда үлкен болатындықтан пайдалы әрекет коэффициенті өте төмен болады. Сондықтан қондырғының, құрылғының бос жүрісін мүмкіндігінше болдырмау керек.
Тізбек элементінің кедергісінің өте азаюы немесе аздығы салдарынан тогының рауасыз өсуі себепті апаттық жағдайдағы жұмыс күйін қысқа тұйықталу деп атайды. Қысқа тұйықталу кезінде қысқа тұйықталу кернеуі
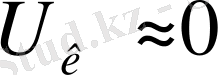 , ал қысқа тұйықталу тогы
, ал қысқа тұйықталу тогы
 болады. Номинал тогынан көп үлкен токтың әсерінен сымдар қызып оқшауы балқиды, жалаңаштанып бір- біріне тұйықталады да, кедергісі одан әрі азаяды. Ток одан әрі өсіп, егер осы уақыт ішінде қорғау тінікілері (элементтері ) іске асырылмаса, тізбектің істен шығып қалуы мүмкін. Сондықтан қысқа тұйықталу тогынан қорғау үшін әр түрлі аспаптар мен сақтандырғыштар қолданылады. Олар қажетті уақыт ішінде іске қосылып, тізбекті қорек көзінен ажыратып, токсыздандырады.
болады. Номинал тогынан көп үлкен токтың әсерінен сымдар қызып оқшауы балқиды, жалаңаштанып бір- біріне тұйықталады да, кедергісі одан әрі азаяды. Ток одан әрі өсіп, егер осы уақыт ішінде қорғау тінікілері (элементтері ) іске асырылмаса, тізбектің істен шығып қалуы мүмкін. Сондықтан қысқа тұйықталу тогынан қорғау үшін әр түрлі аспаптар мен сақтандырғыштар қолданылады. Олар қажетті уақыт ішінде іске қосылып, тізбекті қорек көзінен ажыратып, токсыздандырады.
1. 4 Кирхгофтың бірінші заңы
Әдетте тізбектің түйінінде бірнеше ток ығысып жатады: бірнеше ток түйінге келіп жатса, бірнеше ток түйіннен шығып жатады. Мысалы, 1, 5- суретте b түйінінде
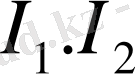 токтары түйінге кіріп жатыр да, ал
токтары түйінге кіріп жатыр да, ал
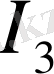 тогы түйіннен шығып жатыр, d түйінінде
тогы түйіннен шығып жатыр, d түйінінде
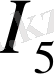 тогы түйінге кіріп,
тогы түйінге кіріп,
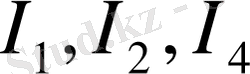 токтары түйіннен шығып, f түйінінде
токтары түйіннен шығып, f түйінінде
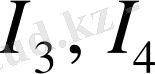 токтары түйінге кіріп,
токтары түйінге кіріп,
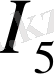 токтары түйіннен шығып жатыр.
токтары түйіннен шығып жатыр.
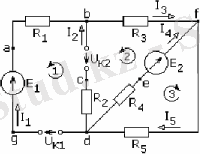
1. 5- сурет Бірнеше қорек көзі бар электр тізбегінің сұлбасы
Тізбек нүктелерінің потенциалдары тізбектегі қорек көздерінің ЭҚК- тері мен тізбек элементтерінің кедергісіне байланысты тізбек бойында әр түрлі мәндерге ие болады. Сондықтан түйінде тоғысқан токтардың бағыттары да ір түрлі болады. Кирхгофтың бірінші заңы осындай түйінде тоғысқан токтардың, яғни түйінге кіріп жатқан токтар мен түйіннен шығып жатқын токтардың ара қатынасын тағайындайды.
Түйінде заряд тудыратын көз болмайтындықтан, Гаусс теоремасы бойынша
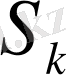 беттік аудан арқылы түйінге кірген зарядтар ағыны
беттік аудан арқылы түйінге кірген зарядтар ағыны
 беттік аудан арқылы түйіннен шыққан зарядтар ағынына тең болады (1. 6- сурет) :
беттік аудан арқылы түйіннен шыққан зарядтар ағынына тең болады (1. 6- сурет) :
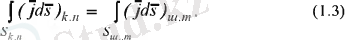
мұндағы
 - түйінге кіріп және түйіннен шығып жатқан зарядтардың тығыздығы;
- түйінге кіріп және түйіннен шығып жатқан зарядтардың тығыздығы;
 - түйін бетінің зарядтар кіріп және шығып жатқан аудандары.
- түйін бетінің зарядтар кіріп және шығып жатқан аудандары.
Зарядтар ағынының ток екенін ескерсе, түйінге кіріп және шығып жатқан токтар:
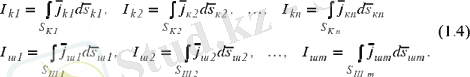
Егер интегралдардың мәндерін (1. 3) теңдікке қойса, онда
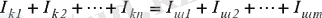
немесе
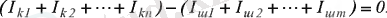
Осы теңдікте түйінге кіріп және түйіннен шығып жатқан токтардың қосындысын қосынды таңбасын пайдаланып жазса, онда
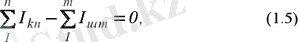
ал жалпы алғанда
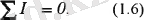

1. 6- сурет Тізбек түйінінің сұлбасы
(1. 5) және (1. 6) өрнектері Кирхгофтың бірінші заңының өрнектері болып табылады. Кирхгофтың бірінші заңы: « түйінге кіріп және түйіннен шығып жатқан токтардың алгабралық қосындысы нөлге тең » (1. 5- өрнек) немесе түйінде « түйінде тоғысқан токтардың алгебралық қосындысы нөлге тең » (1. 6- өрнек ) деп тұжырымдайды.
Кирхгофтың бірінші заңы бойынша өрнектер жазған кезде, (1. 5) -өрнектен көрініп тұрғандай түйінге бағытталған токтар оң таңбамен, ал түйіннен бағытталған токтарды теріс таңбамен алу керек. Мысалы, қарастырылып отырған тізбектің b түйінінде
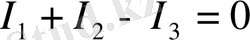 . d түйінінде
. d түйінінде
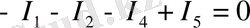 , ал f түйінінде
, ал f түйінінде
 .
.
1. 5 Кирхгофтың екінші заңы
Электр өрісінің потенциалдығына негізделген Кирхгофтың екінші заңы тізбектің кез келген бөлігіндегі кернеулер мен ЭҚК- тердің ара қатынасын тағайындайды.
Потенциалды электр өрісінде бірлік зарядты өрістің бір нүктесінен екінші нүктесіне орын ауыстыртып және оны бастапқы нүктеге қайтып алып келу үшін, яғни тұйықталған контурда істелетін жұмыс нөлге тең:

мұндағы,
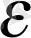 - электр өрісінің кернеулігі;
- электр өрісінің кернеулігі;
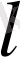 - контурдың ұзындығы.
- контурдың ұзындығы.
Егер контурға ЭҚК кіргізсе, онда заряд бөгде күштің әсерінен орын ауыстырады, яғни

Интегралды қосындымен алмастыра және контурда бірнеше пассивті элемент пен бірнеше ЭҚК бар деп есептелсе, онда

Бұл өрнек « тұйықталған контурда кернеулердің алгебралық қосындысының осы контурдағы ЭҚК-тердің алгебралық қосындысына тең » екендігін көрсетеді. Міне осы тұжырым Кирхгофтың екінші заңы деп аталады.
Электр өрісінің потенциалдығы бойынша «
электр тізбегіндегі
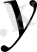 нүктесінің потенциалы зарядтың
нүктесінің потенциалы зарядтың
 нүктесінен
нүктесінен
 нүктесіне қай жолмен орын ауыстырғанынан тәуелді емес
». Ендеше «
тізбектің кез келген екі нүктесінің арасындағы потенциалдар айырымы (кернеу) осы екі нүктені қосып тұрған кез келген тармақтардағы элементтердің потенциалдар айырымының (кернеулердің ) алгебралық қосындысына тең
»:
нүктесіне қай жолмен орын ауыстырғанынан тәуелді емес
». Ендеше «
тізбектің кез келген екі нүктесінің арасындағы потенциалдар айырымы (кернеу) осы екі нүктені қосып тұрған кез келген тармақтардағы элементтердің потенциалдар айырымының (кернеулердің ) алгебралық қосындысына тең
»:
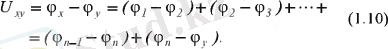
Олай болса, 1. 5- суреттегі тізбектің b және d нүктелерінің арасындағы кернеу:
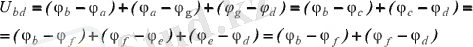
немесе потенциалдар айырымының орнына кернеулер мен ЭҚК- терді қойса және тізбектің пассивті элементінде ток пен кернеудің бағыттыс болатынын ескерсе, онда
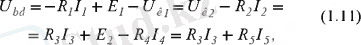
мұндағы,
 - кернеу көздері.
- кернеу көздері.
(1. 11) өрнегінен бірнеше теңдікті алып, ондағы кернеулер мен ЭҚК- терді бөлектеп жазса, онда

Мұндай теңдеулерді тізбектің басқа да нүктелерінің арасындағы потенциалдар айырымы үшін жазуға болады. Ендеше b және d нүктелерін кез келген
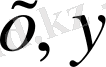 нүктелері деп белгілеп, ал осы екі нүктені қосып тұрған тармақтарда бірнеше пассивті элементтер мен бірнеше кернеу көзі және бірнеше ЭҚК көзінің болу мүмкіндігін ескерсе, онда (1. 12) өрнегін жалпы түрде төмендегіше жазуға болады:
нүктелері деп белгілеп, ал осы екі нүктені қосып тұрған тармақтарда бірнеше пассивті элементтер мен бірнеше кернеу көзі және бірнеше ЭҚК көзінің болу мүмкіндігін ескерсе, онда (1. 12) өрнегін жалпы түрде төмендегіше жазуға болады:
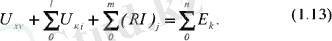
(1. 13) өрнегі (1. 9) өрнегінің кеңейтілген түрі болып табылады: (1. 9) өрнегінің сол жағындағы жалпы кернеудің орнына (1. 13) өрнегінде олар аталып келтірілген.
Ендеше (1. 13) өрнегі бойынша Кирхгофтың екінші заңын былай да тұжырымдауға болады: « тізбектің кез келген екі нүктісінің арасындағы кернеу мен осы екі нүктені қосып тұрған тізбек бөлігіндегі кернеулердің алгебралық қосындысы тізбектің осы бөлігіндегі ЭҚК- тердің алгебралық қосындысына тең ».
Егер тұйықталынған контур қарастырылатын болса, онда екі нүкте арасындағы кернеу ұғымы өзінің мағынасын жояды да (х және у нүктелері беттесіп бір нүктеге айналады,
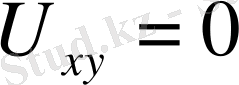 болады), (1. 13) өрнегі мынадай түрге келеді:
болады), (1. 13) өрнегі мынадай түрге келеді:
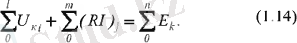
Егер тізбектің қарасытырып отырған бөлігінде кернеу көзі болмаса, онда
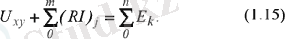
Егер кернеу көзі жоқ тұйықталған контур қарастырылса, онда
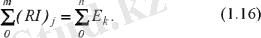
Егер тізбектің қарасытырылып отырған бөлігінде кернеу көзі және ток жоқ болса,

Сонымен, тізбектерді есептеген кезде, қарастырылатын тізбек бөлігінің түріне қарай, Кирхгофтың екінші заңын соңғы бес өрнек түрінде жазып қолдану қажет.
1. 6 Кирхгоф заңдарын тізбектерде есептерде қолдану
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz