Кванттық механикадағы қозғалыстың ерекшеліктері

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 42 бет
Таңдаулыға:

Мазмұны
Кіріспе

I тарау Бірөлшемді қозғалыс
§1.1 Гейзенбергтің анықталмаушылық қатынастары
§1.2 Еркін бөлшектің қозғалысы
§1.3 Кванттық гормониялық осциллятор

II тарау Кванттық механикадағы қозғалыстың ерекшеліктері
§2.1 Потенциалдық шұңқырдағы бөлшек
§2.2 Бөлшектің потенциалдық тосқауылдан өтуі
§2.3 Кванттық осциллятор және оптикалық электрон үшін сұрыптау ережелері

III тарау Кванттық механикадағы есептер шығару әдісі

Кіріспе.

Кванттық механика – микробөлшектердің (элементар бөлшектер,
атомдар, атом ядролары, молекулалар) қозғалысын және олардың бір-біріне
жасайтын әсерлерін зерттейтін қазіргі теориялық физиканың аса маңызды
саласы. Оның ғылым болып қалыптасуы ғасырымыздың бас кезінде ашылған
физикадағы ұлы жаңалықтармен тығыз байланысты.
XXI ғасыр физика ғылымының өте жеделдамыған ғасыры болды.
Классикалық механика тамаша математикалық еңбектердің нәтижесінде жүйелі
аяқталған физикалық теорияға айналды. Электр және магнитизм саласындағы
жетістіктер Максвелдің электромагниттік теориясының ашылуына алып келді, ол
теория оптикалық құбылыстардың табиғаты электромагниттік екендігін толы
түсіндіріп береді. Сөйтіп, классикалық электродинамика қомақты ғылым
саласына айналды. Макроскопиялық денелердің қасиеттерін зерттеу барысында
жасалған тәжірибелердің қорытындысын классикалық механика мен классикалық
электродинамика көмегімен түсіндіру нәтижесінде классикалық статистикалық
физика келіп шықты. Теориялық физиканың жетістіктері дереу адам баласының
практикасында қолданылып, техникалық ғылымдардың дамуына себепші болды (
техникалық механика, электротехника, тнрмодинамика және тағы басқс). Сол
кездегі физиктердің кемшілігі кез келген физикалық құбылысты осы
қалыптасқан физикалық теорияның көмегімен өкжей – текжейлі түсіндіріп
беруге болады деп ойлады. Қысқасы, XIX ғасырдың аяқ ғалымдар арасында
табиғат заңдылықтары түгел бітуге жақын деген пікір орын ала бастады.
Физиканың ары қарай дамуы көп ұзамай ғалымдардың бұл ойын жоққа
шығарды. XIX ғасырдың аяғы мен XX ғасырдың бас кезінде сол кезденгі
физикалық теорияның көмегімен түсіндіруге болмайтын бір қатар фундаметалды
жаңалықтар ашылды, олар: рентген сәулесі, электрон бөлшегі, фотозффект,
радиоактивтілік және тағы басқа. Уақиғаның мұндай күтпеген жерден бетбұрыс
алуы бірқатар физиктер мен философтарды қалыптасқан көзқарастың күйрегенің
мойындауға мәжбүр етті. Бұрынғы басшылыққа алып келген идеялар жөніндегі
бірауыздық, енді ғалымдар арасындағы келіспеушілікпен алмасты. Физиканың
дамуындағы бұл кезең Физиканың дағдарысы деп аталды және ол дағдарыс
физиканы дамудың жаңа сатысына көтерді. Қазір біздің кванттық механиканы
адам баласының табиғат заңдылықтарын танып білу жолындағы жаңа саты болды
деп айтуға толық негізіміз бар.
Кванттық механиканың негізін салған бір-бірімен ол кезде өзара
байланысты болмаған физиканың әртүрлі салаларында соңғы екі ғасырдың
шекарасында жүргізілген эксперименттік жұмыстар: атомдық спектроскопия,
абсолют қара денелердің сәуле шығаруын зерттеу, фотоэффекктіні зерттеу,
қатты денелер физикасы, атом құрылымын зерттеу және тағы басқа.
XIX ғасырдың соңғы жылдарында атомның сәуле шығару спектрлері
жөнінде өте көп эксперименттік мәліметтер жинақталды. Атомның шығаратын
спектрлері белгілі тәртіпппен орналасқан дискретті сызықтар жиынтығы
екендігі белгілі болды. 1885 жылы Бальмер сутегі атомының спектрлік
сызықтарының сериясын ашты, оны қарапайым формуламенен өрнектеп берді. 1889
жылы Ридберг талий мен сынап атомдарының беретін спектрлік сызықтарының
серияларын тапты. 1904 жылы Лайман сутегі атомының спектрдің ультракүлгін
бөлігінде жататын сызықтардың сериясын, ал 1909 жылы Пашен сутегінің
спектрдің инфрақызыл бөлігінде орналасатын сызықтарының сериясын тапты. Бір
ерекшелігі сол – Лайман мен Пашен серияларды да Бальмер формуласына ұқсас
формуламен өрнектеді. Атом спектрлерінің әр түрлі серияларындағы заңдылықты
ескере отырып 1908 жылы Ритц өзінің атақты принципін ұсында. Бұл принцип
1913 жылға дейін өзінің шешімін таппады, спектрлік сызықтардың табиғаты
түсініксіз болып қала берді.
Абсолют қара денеледің сәуле шығаруын зерттеу нәтижесінде 1896
жылы Вин эксперименттік қорытындылардың жоғарғы жиіліктерге сәйкес жағын
ғана түсіндіретін формула тапты. Формула төменгі жиіліктер үшін жарамсыз
болды. 1900 жылы Рэлей төменгі жиіліктерде тәжірибемен сәйкес келетін басқа
формула ұсынды, бірақ бұл формула сәуле шығарудың жоғарғы жиіліктерге
сәйкес бөлігін түсіндіріп бере алмады. Бұл уақиға сол кеде ультракүлгіндік
күйреу деп аталында.
1900 жылы 14 Желтоқсанда Планк Берлин академиясында өзінің
Қалыпты спектрдегі энергияның таралу заңдылығының теориясы деген тарихи
еңбегін тапсырды. Өзіне дейінгі жасалған эксперименттік жұмыстардың
қорытындыларын түсіндіре алатын өзінің атақты формуласын ұсынды. Бұл
формуладан жиіліктің сәйкес облыстары үшін Вин және Рэлей – Джинс
формулаларын алуға болатындығын өрсетіп берді. Планктын даналылығы сонда,
ол осы еңбегінде энергия үздікті, порция (квант) түрінде шығарылады. Және
жұтылады деп түсіндіргі, онын шамасы ε=ħω. Мұндағы ω- циклдік жиілік, ħ-
Плак тұрақтысы. Сондықтан да жоғарыда айтылған күйді белгілі мағынада
кванттық механиканың туған күні деп айтуға болады.
Плактың квантты, гипотезасын пайдаланып, 1905 ж. Эйнштейн сол
кезге дейін түсіндіруге болмай келген фотоэффект заңдылықтарын тамаша
түсіндіріп берді. 1907 ж. Эйнштейн кванттау ережесін көп жыл қтарынан
толғандырып жүрген тағы бір проблеманы шеуге қолданды.Планктын энергияны
кванттау идеясын Эйнштейн кристалдағы атомдардың тербелісіне қолданып,
қатты денелердің жылусыйымдылығының температураға тәуелді болатындығын
көрсететін формула алды. Сол формула тәжірибелерде алынып жүрген қисықтарды
толық түсіндіріп бере алады. Сөйтіп Эйнштейн осы еңбегінде қазіргі кездегі
қатты денелер жылусыйымдылығы теориясының негізін салды.
1915-1916 ж. Зоммерфельд Бор теориясын ары қарай дамытып, кванттау
әдісін еркіндік дәрежесі бірден артық болатын жүйелерге қолданды, сөйтіп
атомдағы электронның тек шеңбер бойымен ғана емес эллипстік орбита бойымен
де қозғала алатын,дығын дәлелдеді. Электронның магниттік моментінің белгілі
бағыттағы проекцияларының квантталатындығын ашып, физикаға кеңістіктік
квантталу ұғымын енгізді. Бұл қағида 1921 ж. Штерн және Герлахтың күміс
атомдарының шоғын күшті әртекті магнит өрісі арқылы өткізген тәжірибесінде
өз дәлелін тапты. Бордың теорияның ары қарай дамуы кезінде оның өзіне тән
ішкі қайшылықтарының бар екендігін сезіле бастады. Бұл қайшылықтарды жеңуге
жарықтың табиғаты жөніндегі екі түрлі көзқарас толқындық және
корпускуларлық үлкен әсерін тигізді.
Дуализм идеясы кванттық механиканың физикалық теория болып
қалыптасуының алғашқы сатысы еді. 1924 ж. Де Броиль өзінің Кванттар
теориясы жөніндегі зерттеулер деп аталатын докторлық диссертациясында
корпускулалық- толқындық дуализм идеясын тек фатонға ғана емес, кез келген
микробөлшекке қолдануға болатындығы жөнінде ұсыныс жасады. Көп ұзамай бір
мезгілде бірнеше лобороторияда жүргізілген эксперименттік жұмыстар
электронның толқындық қасиетінің бар екендігін үзілді- кесілді дәлелдеп
бернді.
Планктың кванттау идеясы мен дуализм идеясын өзара ұштастыру
кванттық механиканың дамуына өте үлкен әсер жасады. 1925-1926 ж. Гейзенберг
пен Шредингер еңбектері кванттық механиканы жүйелі физикалық теорияға
айналдырды.
20 - жылдардың ішінде дамыған кванттық механиканы әдетте
релятивистік емес кванттық механика деп атайды- ол жылдамдығы жарық
жылдамдығымен салыстырғандағы өте аз болатын микро бөлшектердін кванттық
механикасы. Кез келген мүмкін болатын жылдам қозғалатын бөлшектер үші
жазылған кванттық теория релиативистік кванттық механика деп аталады, ол 30-
жылдарда қалыптасты. Міне, 40 жылдан бастап астам уақыт релятивистік
кванттық механикадан бөлініп шығып, өз алдына ғылым саласына айналған,
атомдағы , ядродағы және элементтар бөлшектердегі құбылыстарды түсіндіретін
физикалық теориялар кванттық электродинамика және өрістін кванттық теориясы
болып дамуда.
Көріп отырғанымыздай қазіргі кванттық механика дамып келе жатқан,
әлі соңғы тараулары жазылып бітпеген физикалық теория. Ол тек ғылыми
көзқарастарда ғана емес, сонымен бірге техникада айтарлықтай революция
жасауда. Біз атомдық электростанциялардан беретін тогын пайдаланудамыз.
Бізді қоршаған радиоқабылдағыштар мен телевизорларда жартылай өткізгішті
кванттық техника қолданылады. Жұмысы кванттық құбылыстарға негізделген
интегралдық схемаларды пайдаланатын калькуляторлар мен компьютерлер
тұрмысымызға кеңінен еңуде. Халық шаруашылығы мен медицинада кванттық
сәулелер көздері қолданылуда. Материяның кванттық қасиетіне негізделіп
асқын өткізгіштерден жасалған магниттерді пайдаланып келеміз. Кванттық
механика Әлемнің пайда болуы мен эволюциясы жөніндегі біздің көзқарасымызды
толық өзгертуде.

§1.1 Гейзенбергтің анықталмаушылық қатыстары.
1. Бөлшектердің корпускулалық – толқындық қасиеті және
кеңістіктегі бөлшектер күйін анықтайтын ψ – функциясының статистикалық
мағынасы класикалық физикадағы ұғымдардың микродүниеде қолданылу шекарасы
жөніндегі маңызды мәселеге алып келеді. Кез келген толқындық процесс үшін
орындалатындығын айттық, олай болса аталып отырған теңсіздіктер де Бройль
толқындары үшін де орындалады. Егер бұл теңсіздіктердегі ω және к
микрообьектінің толқындық сипаттамалары десек, онда теңдеулерін пайдаланып
микрообьектінің корпускулалық сипаттары үшін де осыларға ұқсас қатыстар
аламыз:

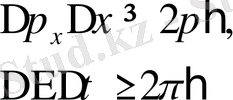(1.1)
Бұл қатыстарды алғаш рет Гейзенберг тапқан болатын, сондықтан бұ
теңсіздіктер Гейзенбергтің анықталмаушылық қатыстары деп аталады. Бұл жерде
импульске Х- индексін бердік , өйткені жалпы жағдайда басқа координаталар
нольге тең болмауы мүмкін, онда мынадай қатыстар орындалады:

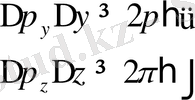(1.2)
Алдымен қатыстарын талқылайық. Бұл формуладағы -де бройль толқынымен
сипатталатын бөлшектің табылатын координаталар интервалдары, ал
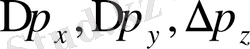бөлшектің импульсінің сәйкес осьтердегі проекциясын қамтитын
интервалдар. Көріп отырғанымыздай, олар белгілі дәрежедегі дәлсіздікпен
анықталады екен және олардың мәні бір мезгілде нольге тең бола
алмайды.Басқаша айтқанда , координата және импульс классикалық
ұғымдарын микробөлшектер қозғалысын сипаттау үшін қолданғанда олардың өзара
Гейзенберг қатыстары арқылы байланысатындығын ескеруіміз керек. Мысала,
электрон Х осінің ∆Х интервалында орналасқан болса, онда оны шексіз ұзаққа
созылған монохраматты де Бройль толқынымен сипаттай аламыз. Электронның ∆Х
интервалында болуы 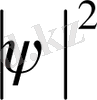тың ∆Х интервалының сыртында нольге айналып
кететіндігін көрсетеді, сондықтан электронды осы шартты қанағаттандыратын
етіп жазық монохраматты де Бройль толқындарының жиынымен сипаттауымыз
қажет.
Ондай толқын пакетін сипаттайтын ψ функцияның модулінің квадраты (ψ)2 х
осінің ∆х интервалынан басқа жерде нольге айналып кетуі тиіс. Ондай қорытқы
толқынның белгілі жиілігі (толқынның саны) болмайды, олай болса электрон
импульсінің дәл мәні жоқ. Электрон импульсі тек Гейзенберг қатыстары
белгілеген 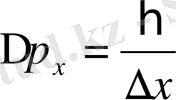дәлдікпен ғана анықталады. Керісінше , егер электронның
импульсі ∆рх интервалында берілген болса , онда электрон бірге тең
ықтималдықпен 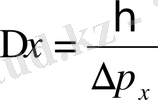интервалынан табылады. Бұл айтылғандардан
микрообьектінің координатасы мен импульсінің бір мезгілде өлшеуге
болмайтындығын көріп отырмыз. Бұл – микробөлшектердің тек өздеріне ғана тән
ерекшелігінің көрінісі, Гейзенбергтің анықталмаушылық қатыстары міне
микробөлшектердің осы обьективтік қасиеттерін ғана көрсетіп беріп отыр.
Енді (1,1) қатыстарына тоқталайық. Микрообьектінің күйі тұрақты
болмасын деп жориық және белгілі күйде өмір сүру уақыты ∆t болсын. Ондай
жағдайда микробөлшектің энергиясы Е – ның анықталмаушылығ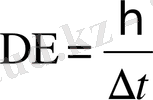ы болады.
Егер микрообьектінің күйі шексіз тұрақты болса (∆t→∞), онда оның энергиясы
дәл анықталады (∆E→∞). Мысал ретінде атомның Е1,Е2 ,Е3 , ... . дискретті
күйлерін алайық. Әр деңгейдің белгілі ені бар, деңгей жоғарылаған сайын
оның ені кеңи түседі. Бұл атомның қозған күйде өмір сүре алу уақыты қысқа.
Атомның негізгі күйде өмір сүре алу уақыты ұзақ болғандықтан, оған сәйкес
деңгейдің ені шексіз жіңішке болады.
Сонымен, Гейзенбергтің анықталмаушылық қатыстары классикалық
ұғымдарды микрообьтілерінің қозғалысын сипаттау үшін қалай болса солай
қолдана беруге болмайтындығын, оларды белгілі дәрежеде шектеу керек
екендігін көрсетеді. Бұл қатыстардың классикалық физикада сезілмеуі
қарастырылған денелер массасының өте үлкен екендігі мен байланысы.
Шындығында 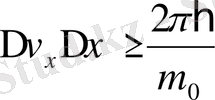болғандықтан, координата мен импульстің
анықталмаушылықтары өте аз шама болады. Мысалы, 10-13кг тозаңның сызықтық
өлшемі анықтағанда жіберілген қате ∆x~ 10-8 м болғанның өзінде
жылдамдығының анықталмаушылығы ∆v~ 10-13мс болады. Әрине мұндай
анықталмаушылықтарды тозанның барлық жылдамдықтарының мәнінде сезуге
болады.
2. Праграфтың бас жағында келтірілген Гейзенберг қатыстарын алу жолы
оқырманға формальды және дәлелі аз сияқтанып көрінуі мүмкін. Шындығында,
қатыстардың орындалатындығын бұлтартпай дәлелдейтін мысалдарды көптеп
келтіруге болады. Солардың бір – екеуін қарастырайық.
а. Микрообьектінің дифракциясы. Импульсі Р болатын бөлшектер ағынының
алдына ені d болатын саңлау қойылған делік. Х – осін бөлшектер ағынына
перпендикуляр бағытта алыйық. Саңлаудан өткен микробөлшектер экранда
дифракция құбылысын береді. Бірінші дифракциялық максимумның көріну бұрышы
θ болсын, онда дифракциялық максимум алу шарты бойынша dsinθ=λ θ бұрышының
аз екндігін ескеріп, бұдан мынадай қатыс аламыз:

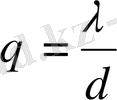(1.3)
Мұндағы λ де Бройль толқыны екендігін еске алып, (1,3) былай жазамыз:

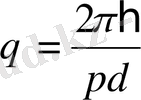(1.4)
Бөлшек саңылаудан өткенде оның импульсі ∆рх қа өзгереді, ∆рх≈рθ екендігін
оңай тауып аламыз. Бұған (1,3) - тен θ – ның мәнін қойсақ, 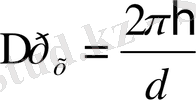шығады.
Саңлау ені d≈∆x- бөлшек координатасының анықталмаушылығы, осыдан ∆рх∆x≈2πħ,
немесе анықталмаушылық қатыс шығады.
б. Оптикалық микроскоппен микробөлшектің орнын анықтау.
Оптикалық микроскоппен қандай да бір микробөлшектің кеңістіктегі орнын
анықтау қажет делік. Оптикалық микроскоптың шешу қабілетінің төменгі шегі:

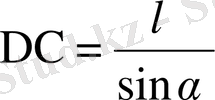(1.5) мұндағы λ – бөлшекке
түсіретін бөлшек түсіретің жарықтың толқын ұзындығы, α –аппаратура
бұрышының жарысы. Егер бөлшекке жарық сәулесін Х – осінің бойымен түсіретін
болсақ, онда бөлшек импульсінің анықталмаушылығы фотон импульсімен
анықталады немесе:

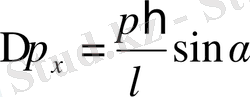(1.6)
Егер бөлшекке қысқалау толқын ұзындықты жарық жіберсек, онда ∆x азаяды,
бірақ жарық квантының импульсі көбейіп кетеді.
Олай болса, бөлшектің координатасын анықтауда жіберетін қателер табылады.
Осы екі өрнекті көбейтіп, бұл жағдайда да анықталмаушылық қатыстардың орын
алатындығына көз жеткіземіз, немесе
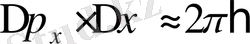
3. Анықталмаушылық қатыстарды пайдаланып қарапайым жолмен өте аз маңызды
қорытындылар алуға болады. Бірнеше мыса келтірейік.

а. Сутегі атомының негізгі күйінің энергиясын шамалау
Кулондық өрісте қозғалатын заряды бар бөлшектің энергиясының
классикалық өрнегін жазайық:

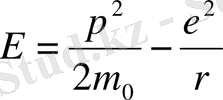(1.7)
мұндағы mе – электрон массасы, е – электрон заряды, r - өріс центірінен
электронға дейінгі қашықтық. P және r шамаларын импульс пен координата
анықталмаушылықтары ретінде алайық, онда pr=2πħ. Осыны пайдаланып r – ді
шығарып тастайық:

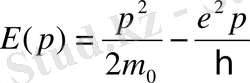(1.8)
Бұл функциясының минимум мәні E1 импульсінің 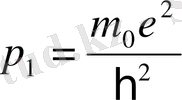мәніне сәйкес келеді,
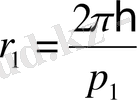екендігін ескеріп, r1 және E1 табамыз:

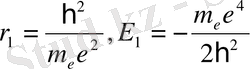(1.9)
Сутегі атомындағы электронның бірінші орбитасының радиусының (Борлық
радиустың) және ең төменгі энергетикалық деңгейдің дәл мәндерін алдық.

б. Осциллятордың нольдік тербелісінің энергиясын шамалау.
Бір өлшемді классикалық гармониялық осциллятордың энергисы
былайөрнектеледі:

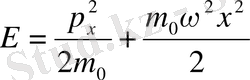(1.10)
Рх пен Х – ты импульс пен координатаның сәйкес анықталмаушылықтары ретінде
алсақ, онда Рх·Х≈2πħ. (1.10) теңдеуіндегі Х – ты 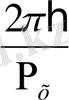пен ауыстырамыз,
сонда

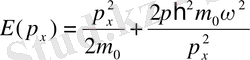(1.11)
Бұл функциясының нольдік мәні Е0 импульсінің мәніне сәйкес келеді, олай
болса

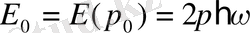(1.12)
Дәл есептеу 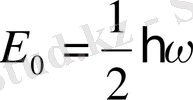екендігін көрсетеді. Бұл алынған қорытынды кванттық
осциллятордың нольдік тербелісінің энергиясы ħω шамасындай болатындығын
анықтайды. Осы айтылған мәселе тағы бір қорытынды жасауға негіз болады.
Микрообьект потенциалдық шұңқыр түбінде жататын болса, онда оның импульсі
(анықталмаушылығы да) нолге айналады. Ондай жағдайда координатаның
анықталмаушылығы шексізге ұмтылады. Бұл бөлшектің шұңқырды болу фактісіне
қайшы келеді.

в. Атомдағы электронның ядроға құлап түспеуін түсіндіру.
Сутегі атомы жөніндегі Бор теориясы атомдағы электронның не себепті
электромагниттік сәуле шығармайтындығын және ядроға құлап түспейтіндігін
түсіндіріп бере алмады.
Гейзенбергтің анықталмаушылық қатыстары туралы мәселені оңай
түсіндіріп береді. Электрон ядроға құлап түссе, онда оның координатаның
анықталмаушылығы күрт кемиді. Алдында электрон сызықтың өлшемі ~10-10м
болатын атом ішінде болған болса, енді ол сызықтың өлшемі ~10-14м болатын
ядро ішінде болады. (1.1) қатысы бойынша, ондай жағдайда, электронның
импульсінің орташа мәні, ол қосымша энергияны қажет етеді. Олай болса,
электрон өздігінен ядроға құлап түспейді. Есептеулердің көрсетуі бойынша
электрон ядроға құлап түсуі үшін сутегі атомының энергиясын шамамен 10 эв
тан 109 эв ке дейін көтеру қажет болады. Онда электронның энергиясы
ядродағы нуклонның байланыс энергиясынан да (~107 эв) артық болып кетеді.
Сондықтан электрон ядроның потенциалдық шұңқырында орналаса алмайды. Біз
сапа жағынан тек электонның ядроға құлап түсе алмайтындығын ғана емес,
сонымен бірге электронның ядро құрамында бола алмайтындығын да түсіндірдік.

г. Тунельдік эффект.
Классикалық механика энергиясы Е болатын бөлшек биіктігі UЕ болатын
потенциалдық тосқауылдан өте алмайды деп түсіндіреді. Микрообьектілер үшін
анықталмаушылық қатыстары (1.2) бұл мәселені басқаша түсіндірді.
Қозғалыстағы микрообьект потенциалдық тосқауылға келіп соққанда, онымен
әсерлеседі, әсерлесу уақыты ∆t болсын. Бұл кезде оның энергиясы

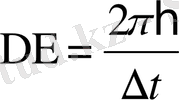(1.13)
анықталмаушылықпен потенциалдық тосқауыл биіктігімен шамалас болса, онда
ол тосқауыл бөлшек үшін кедергі бола алмайды, микрообьект потенциалдық
тосқауылдан өтіп кетеді. Бұл – таза кванттық құбылыс, оны тунельдік эффект
деп атайды.

д. Микробөлшектер траекториясы.
Қандай да бір бөлшектің траекторисын сызу үшін әр уақыт моментіндегі оның
координатасы мен импульсінің дәл мәндері белгілі болуы тиіс. Ал
анықталмаушылық қатыстардың түсіндіруі бойынша микрообьект бір мезгілде
координатаның және оған сәйкес импульс проекциясының дәл мәнін қабылдай
алмайды. Сондықтан. Дәлірек айтсақ. Кванттық механикада микробөлшектерге
траетория ұғымы қолдануға болмайды. Траектория ұғымынан бас тартуымыз
микробөлшектерді классикалық корпускула тәрізді қарастыра алмайтындығымызға
байланысты, өйткені, енді микробөлшектердің толқындық қасиетін ескеруіміз
керек. Кейбір t уақыт моментндегі оның координатасы Х белгілі болғанымен,
t+dt моменті үшін оның координатасының мәні қандай болғанымен алдын ала
айта аламыз. Демек, Бор теориясындағы атомдағы электронның орбитасы деген
ұғым дұрыс емес. Тек электронның атом ішінде екендігін ғана айта аламыз.
Сондықтан, атомның Планетарлық моделі – атом жөніндегі біздің түсінігімізді
даму процесіндегі аралық этап ғана.
Дегенмен, кейбір жағдайларда бөлшектер траекториясы ұғымын
пайдалануға болады. Мысал ретінде телевизор кинескопындағы электорндар
қозғалысын қарастырайық. Электрон шоғын жасаудың өзі ағынға көлденең
бағыттағы координатаның жинақталғанын көрсетеді, жинақталу дәрежесі
электрон шоғының диаметрі d – мен анықталады. Бұл бағыттағы импульстің
анықталмаушылығы (1.1) бойынша , оның әсерінен электрон бұрышқа
ауытқуы мүмкін. Егер электронның кинескоп ішіндегі жүретін жолының
ұзындығы L болса, онда электронның экранға барып соғатын нүктесінің
координатасының анықталмаушылығы болады. U=20 кВ, d=10-5м, L=1м дегенде,
∆х=10-7м болады. Олай болса, анықталмаушылық қатыстарға байланысты
электронның экрандағы орнының ауытқуы электрон шоғының диаметрінен жүз
еседей аз. Әрине, мұндай жағдайда электрон үшін траектория ұғымын
пайдаланса болады. Бөлшектердің фотопластинкада алынатын іздерін, Вильсон
камерасындағы және көпіршікті камерада алынатын тректерін дәл жоғарыдағыдай
әдіспен түсіндіруге болады.
4. Гейзенбергтің анықталмаушылық қатыстарын негізге алып, кейбір идеалистік
бағыттағы философиялық ағымдар қате қорытындылар жасайды.
а. Агностицизм.
Бұл ағымдағы философтар дүниені танып білуге болмайды деп есептейді.
Анықталмаушылық қатыстардың көрсетуі бойынша микробөлшектің бір мезгілде
импульсі мен координатасын дәл өлшеуге болмайды, олай болса бөлшектің күйін
еш уақытта біліп болмайды. Осыдан дүниені танып білуге болмайтындығын
жөнінде қорытынды жасайды. Ал, шындығында микробөлшектің күйін координата
мен импульс емес толқындық функция анықтайды. Олай болса макробөлшектер
күйін зерттеуге болмайды. Микродүниені де түсініп білуге болады, бірақ
түсіну жолы микродүниені түсіну жолынан басқа.
б.Субьективтік идеализм.
Бұл философтар өлшеуіш құралдары мен бақылаушыға ерекше роль береді.
Микробөлшектердің дүниеде бар екендігін жөнінде және олардың күйі туралы
мағлұмат эксперимент жасаушыға тек құрал арқылы ғана келеді, сондықтан
өлшеуіш құралдар болмаса – микробөлшектер де жоқ - деп түйеді. Бірақ,
микробөлшектердің табиғатта бар екендігі – обьективтік шындық, оның дәлелі
көп. Микробөлшектердің күін толқындық функциясымен сипаттау барлық жағдайда
эксперимент қорытындылрымен сәкес келеді.

§1.2 Еркін бөлшек
Бұл тарауда Шредингер теңдеулерін бірөлшемді қарапайым кванттық механикалық
есептерді шешу үшін қолданамыз. Еркін қозғалатын бөлшек алайық, ондай
бөлшек үшін U-0, сондықтан Шредингердің стационар теңдеуін былай жазамыз:

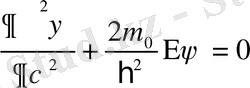(1.14)
Егер осындағы 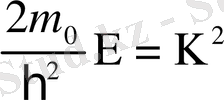деп белгілесек, онда (1.14) қысқаша былай жазылады:

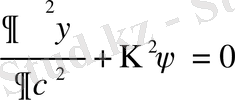(1.15)
мұндағы 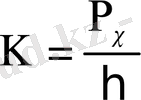- толқындық сан
Бұл қарапайым екінші ретті дифференциалдық теңдеу, оның шешімін
мына түрде жазамыз:

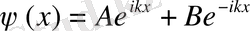(1.16)
Алынған шешімнің физикалық мағынасын түсіну үшін толық толқындық функцияның
жазайық:

(1.17)
Мұндағы бірінші қосылғыш бөлшектің оң бағыттағы қозғалысын, ал екінші
қосылғыш- теріс бағыттағы қозғалысын сипаттайды. Оған фазалық
жылдамдықтардың бағытын анықтау арқылы көз жеткізуге болады. Егер бөлшектің
белгілі бағыттағы қозғалысын қарастыратын болсақ онда (1.14) теңдеуінің
шешуін былай жазамыз:

(1.5)
Бұдан біз еркін бөлшектің қозғалысы кванттық механикада қарапайым жазық
монохраматты де Броиль толқынымен сипатталатындығын көріп отырмыз. Энергия
Е – нің кез келген мәнінде (1.14) теңдеуінің бір мәнді, шекті және үздіксіз
шешуі бар, олай болса еркін бөлшек энергияның үздіксіз мәндерін қабылдайтын
болып шықты. Бөлшекті кеңістіктің кез келген нүктесінде ұшырастырудың да
ықтималдылығы бірдей, өйткені:

(1.19)
Біз жоғарыда еркін бөлшектің импульсі қозғалыс интегралы болатындығын
айттық, ол- еркін бөлшектің импульсі тұрақты болады деген сөз. Еркін
бөлшектің импульс тұрақты болады деген сөз. Еркін бөлшек үшін кванттық
Пуассон жақшасының нолге тең болуы, оның энергиясы мен импульсін бір
мезгілде өлшеуге болатындығын көрсетеді.
2. Еркін бөлшектің меншікті мәндерінің спектрі үздіксіз болғандықтан, оның
меншікті функцияларын бірге нормальдау мүмкін емес өйткені

(1.20)
Сондықтан оны екі түрлі жолмен нормальдайды, сол әдістерін қарастырайық.
а) Алдымен өзіміз айтқандай δ - функцияға нормальдау түсіндірейік. Екі
меншікті функция үшін шартын жазайық:
(1.21)
мұндағы δ-функциясын интегралы арқылы былай жаза аламыз:

(1.22)
(1.21) (1.22) теңдіктерін салыстыра отырып А коэффициентін табамыз:

(1.23)
Сонымен δ-функцияға нормальданған, еркін бөлшектін күйін сипаттайтын
үздіксіз меншікті функция төмендегідей болып жазылады:

(1.24)
б) Меншікті функцияларды нормальдаудың екінші әдісін Борн ұсынған. Мұнда
шекаралық шарттардың орнына ψ функция үшін периодтылық шарты енгізіледі,
немесе
L)
(1.25)
мұндағы L-периодтылықтың ұзындығы.Периодтылық шарты бойынша беггілі. Бұл
теңдік орындалуы үшін

(1.26)

болуы тиіс, мұндағы n = 0,
Табылған К - ның мәндерін пайдаланып еркін бөлшек энергиясының спектрін
жазуға болады:

(1.27)
Сонымен , жасанды жолмен периодтылықтың ұзындығын ендіру нәтижесі де, біз
энергияның үздіксіз мәндерән дискретті мәндермен айырбастадық. Бұл жағдайда
жіберілтін қате L ұзындығына байланысты. Тетелес энергия мәндерінің
айырымы

(1.28)
Мұндағы v- бөлшек жылдамдығы. Егер L, басқаша айтқанда энергия спектрі
үздіксіз болады.
Ψ-функциясы L кесіндісінде периодты болғандықтан, оны нормальдаудың шартын
былай жазамыз:

(1.29)
Бұл алынған формулаға (1.18) бойынша ψ функцияларының мәнін қойып, оңай

(1.30)
екендігін таба аламыз. Сондықтан нормальданған шешім төмендегіше болып
жазылады:

(1.31)
Еркін бөлшекті сипаттайтын бұл табылған функциялар тек нормальданған
ғана болып қоймай, сонымен қатар олар өзара ортогональды да болады,
шындығында теңдігі бойынша:
(1.32)
Еркін бөлшек үшін шешілген бұл бірөлшемді есепті үшөлшемді кеңістік үшін
оңай жалпылауға болады, бірақ алынатын қорытындылардың ешқандай өзгешілігі
болмайды.

§1.3 Кванттық гормониялық осциллятор.
1. Гормониялық осциллятор жөнінднгі есеп теориялық физикадағы маңызды
есептердің бірі болып есептеледі. Ол физиканың әр түрлі саласында
қолданылады, мысалы- механикада, классикалық электродинамика,
радиофизикада, оптикада, атом физикасында және т.б. Бұл есеп сәуле шығару
теориясын жасауда, спектрлер теориясы мен жылусыйымдылық теоияларын құру
үшін нақты түрде қолданылады.
Гомониялық осциллятор деп квазисерпімді күштің әсерінен бірөлшемді
тербеліс жасайтын бөлшекті айтады, оның потенциалдық энергиясын мынадай
формула өрнектейді:

(1.33)
Мұндағы ω- циклдік тербеліс жиілігі, сондықтан кванттық гормониялық
осциллятор үшін Шредингер теңдеуін былай етіп жазамыз:

(1.34)
Белгілеулер енгізейік

(1.35)
және жаңа айнымалы қолданайық:

(1.36)
Ендіріген белгілеулер мен жаңа айнымалы көмегімен (1.34) теңдеуін көшіріп
жазайық:

(1.37)
Бұл теңдеудің z кезіндегі асимтаттық шешуін табайық, ондай жағдайда z2-
қарағанда γ ны ескермеуге болады, сондықтан (1.34) теңдеуі мына түрге
келеді:

(1.38)
Мұндай дефференциалдық теңдеудің шешуі

(1.39)
Түрінде ізделеді. z толқындық функция шектелген болу үшін В=0 болуы
тиіс және ең сонында толқындық функцияның нормальданатындығын ескере отырып
(1.38) теңдеудің шешуі былай жазылады:

(1.40)
Асимтоттық шешу (1.40) көмегімен (1.37) теңдеуінің шешуін жазайық:

(1.41)
мұндағы f(z) қандай да бір функция.
Соңғы алынған теңдеуден ψ дің және ψ11мәндерін (1.37) теңдеуіне қойып,
сәйкес қысқартулардан кейін оны мына түрде жазамыз:

(1.42)
Алынған екінші ретті дифференциалдық теңдеуінің шешуін дәрежелік қатар
түрінде іздейміз:

(1.43)
Осыдан f және f тауып оларды (1.42) теңдеуіне апарып былай жазамыз:
(1.44)
Соңғы теңдеу z тің бірдей дәрежелерінің алдындағы коэффициенттерінің
қосындысы нолге тең болғанда ғана орындалады сондықтан zк ның алдындағы
коэффициенттер қосындысын нолге теңеп жазайық:

(1.45)
Мұнан төмендегідей рекуренттік қатыстар аламыз:

(1.46)
Алынған өрнек ак коэффициенті белгілі болғанда коэффициентін есептеп
таба беруге болатындығын көрсетеді:
(1.41) түрінде ізделініп отырған ψ функциясы шекті функциясы болуы
үшін f функциясын шексіз дәрежелік қатар түрінде ала алмаймыз, сондықтан
оны n-ші дәрежеде үзіп, тек полином түрінде ғана алуға мәжбүр боламыз,
немесе

Онда (1.46) теңдеуінен мынадай формула аламыз:

(1.47)
Егер алынған формулаға (1.35) – тен γ –ның мәнін қоятын болсақ, (1.34)
Шредингер теңдеуінің меншікті мәндерін аламыз:

(1.48)
Мұндағы n=0,1,2,3 ... –кванттық сандар. Сөйтіп, біз кванттық гормониялық
осциллятордың энергиясы квантталатындығын көріп отырмыз. Тағы да мынадай
екі қорытынды жасауға болады: біріншісі - кванттық осциллятордың
энергетикалық деңгейлері бір – бірінен бірдей қашықтықта жатады; екіншісі
-кванттық осциллятордың ең аз энергиясы ешқашан нольге тең болмайды.
Кванттық осциллятордың ең аз энергиясын - - нольдік энергия деп
атайды, оның шындығында осылай екендігін анықталмаушылық қатыстар көмегімен
де дәлелденгенбіз.
Кристалдардағы атомдар кванттық осциллятор мысалы бола алады.
Кристалдардан жарықтың шашырауын зерттейтін тәжірибелер нольдік энергияның
болатындығын толық дәлелдеп беріп отыр. Кристалдан шашыраған жарықтың
интенсивтілігі ондағы атомдардың тербелісіне байланысты. Кристалдың
температурасы төмендеген сайын шашыраған жарық интенсивтілігі белгілі шекті
мәнге ұмтылады, бұл- атомдар тербелісі абсолют ноль кезінде де тоқтамайды
деген сөз.
2. Шредингер теңдеуінің меншікті функцияларын іздеуді
жалғастырайық. Жоғарыдағы келісіміз бойынша f функциясын n дәрежелі полином
екен, оны мына түрде жазайық:

(1.49)
Толқындық функцияның соңында нормальданатындығын ескеріп, деп
алайық, онда формуласының көмегімен коэффициенттерін оңай
таба аламыз:

және т.б.
Осы коэффициенттер көмегімен жазылған полином Эрмит полиномы деп аталады,
оны әдетте деп белгілейді:
(1.50)
Қарапайым Эрмит полиномдарын жазайық:
(1.51)
Эрмит полиномын мынадай тұйық түрде де жазуға болады:

(1.52)
Сонымен біз іздеген екен, онда (1.42) формуласын мына түрде жаза
аламыз:

(1.53)
Айтылған мәселелерді қорыта келіп, гормониялық осциллятор үшін Шредингер
теңдеуінің шешуін былай етіп жазамыз:

(1.54)
Мұндағы - нормальдау коэффициентті, Z айнымаласы X пен (1.36) арқылы
байланысады. Cn коэффициеттерін функциясының нормальдау шартынан
табамыз:

(1.55)
Формуладағы бір орнына (1.52) бойынша мәнін қояйық:

(1.56)
Математикадағы туындыны бір функциядан екінші функцияға ауыстыру ережесі
бойынша немесе (1.56) n рет бөлшектеп интегралдау нәтижесінде
мынадай өрнекке келеміз:
(1.57)
Мұндағы
(1.58)
Осыдан
(1.59)
Сонымен Шредингер теңдеуінің меншікті функцияларын мына түрде аламыз:
(1.60)
Гормониялық осциллятордың жеке күйлері үшін меншікті мәндермен меншікті
функцияларды жазайық:

Жазылған меншікті мәндер мен меншікті функциялардың графиктері және
потенциалдық шұңқырдың түрі (1.3 - суретте) келтірілген.
F(x) функциясындағы Х ті –Х пен ауыстырғанда F(x)=F(x) болса, онда
F(x) функциясын жұп функция деп, ал F(-x)=-F(x) болса, ондаF(x) функциясын
тек функция деп атайды. Гормониялық осцилляторды, меншікті функциялары n-
нің жұп , немесе тақ функция болуы n санына байланысты. Егер n тақ болса,
онда ол тақ функция болады. Меншікті функциялардың графиктері бұл тұжырымды
толық дәлелдейді.
3. Енді гормониялық осцилятордың меншікті функцияларының өзара
ортогональды болатындығын көрсетейік:

Айталық nm делік. Соңғы интегралды полиномын (1.52) тұйық түрімен
алмастырайық, сонда

Туындыны ауыстыру ережесін пайдаланып өрнекті көшіріп жазайық:

Бұл интегралдағы

өйткені m ретті Эрмит полиномынан n ретті туынды алынып отыр, ал келісуіміз
бойынша n›m, сондықтан
(1.61)
Сонымен гормониялық осциллятордың меншікті функциялары үшін ортонормальдану
шартын төмендегіше етіп жазуға болады:
(1.62)
Гормониялық осциллятор үшін меншікті мәндер мен меншікті функциялар
осцилляторды сипаттайтын Гамильтон операторының меншікті мәндері мен
меншікті функциялары екендігін ұмытпауымыз керек. Гамильтониан - өздік
түіндес оператор, сондықтан оның меншікті функциялары өзара ортогональды
болуы тиіс. Алынған нәтижелер оны толығынан растап беріп отыр.

§2.1 Потенциалдық шұнқырдағы бөлшек
1. Шексіз терең шұңқыр
Потенциалдық энергиясы мынадай шарттарды қанағаттандыратын
бірөлшемді өрістегі бөлшектің күйін зерттейік:
(2.1)
Осыған байланысты 0≤х≤а облысында шексіз терең потенциалдық шұңқыр бар деп
есептейді. (2.1 - сурет) Потенциалдық шұңқыр ішінде орналасқан бөлшек
қозғалысын сипаттайтын толқындық функция х=0 және ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.