Конденсирленген орталардағы дыбыс жұтылуы мен кристалдық тордағы фонондардың таралуының теориялық және есептеу негіздері


МАЗМҰНЫ
КІРІСПЕ
Теориялық бөлім
Конденсирленген орталардағы дыбыс жұтылуының қысқаша теориясы
Кристалдық тордың тербелістері және фонондар
Кристалдардың жылулық қасиеттері
Дыбыстық фонондардың жылулық фонондармен әсерлесуі
Дыбыстық толқындардың жылулық фонондармен әсерлесуін макроскоппен қарастыр
Конденсирленген орталардың кристалдық торындағы жылулық фонондардың таралуын есептеу
Конденсирленген орталардың кристалдық торындағы ультрадыбыстық жұтылуды есептеу
Қатты денелердің кристалдық торының акустикалық параметрлерін фонондық теория негізінде зерттеу
Қатты денелердің кристалдық торындағы Дебай температурасын және Дебай жиілігін есептеу
Металдар мен қорытпалардағы дыбыстың жұтылуын бағалау
Cэндвичтердегі дыбыстың жұтылуы
Кремнийдегі жылулық фонондардың қозғалысын зерттеу . . .
Кремнидің жұқа бетінің жылуөткізгіштігінің температураға тәуелділігінің есептеулері
Кремнийдің жұқа қабатындағы жылуөткізгіштігін есептеу
Конденсирленген орталардағы дыбыс қысымының таралуы
Акустикалық сэндвичтің физикалық мағынасы
Сэндвичтердегі дыбыстың жұтылуын есептеу
Ауа-метал, метал-ауа орталарының шекарасындағы және болаттың әртүрлі маркалары арсындағы акустикалық кедергілерді есептеу
Металл-диэлектрик және диэлектрик- метал қабаттарынан тұратын «сэндвич» тегі дыбыс энергиясынынң шығынын есептеу
Кристалдық денелердің көлемді қабаттарында дыбыс жұтылуынынң таралуын есептеу
7
Қоспалардлың дыбыс жұтқыштыққа әсері
7. 1
Қоспалы металдардағы акустикалық толқындардың жұтылуы
7. 2
Радиациялық өрістегі нүктелік ақаулардың пайда болуы
ҚОСЫМША I
Дислокациялық дыбыс жұтылу
ҚОРЫТЫНДЫ
ҚОЛДАНЫЛҒАН АДЕБИЕТТЕР
БЕЛГІЛЕУЛЕР МЕН ҚЫСҚАРТУЛАР
 - ортаның акустикалық импедансы,
- ортаның акустикалық импедансы,
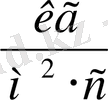 ;
;
h - Планк тұрақтысы;
υ
LL, L
- материалдағы қума дыбыстық толқынның жылдамдығы,
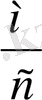 ;
;
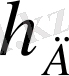 - дыбысжұтқыштың қалыңдығы,
- дыбысжұтқыштың қалыңдығы,
 ;
;
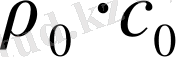 - материал немесе ортаның акустикалық кедергісі,
- материал немесе ортаның акустикалық кедергісі,
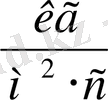 ;
;
Ω - дыбыс жиілігі,
 ;
;
ω - кристалдық тордың тербеліс жиілігі;
ω
D
- Дебайдың кристалдық торының тербеліс жиілігі,
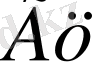 ;
;
Т - температура, К;
γ - Грюнайзен коэффициенті;
k Б - кристалдық тордың қатаңдық коэффициенті (қатаңдық дәрежесі) ;
α - дыбысжұту коэффициенті;
р (ДҚД) - дыбыстық қысым деңгейі, Па;
ДЖК - Дыбысжұту коэффициенті;
ОК-оқшаулағыш кремний;
SOI - төсеніштегі кремний;
УДЖК - ультрадыбыстық жұту коэффициенті;
МЖМТ - Мемлекеттік жалпыға міндетті талап;
КІРІСПЕ
Ультрадыбыстың конденсирленген орталардың кристалдық торлармен әсерлесуін зерттеу, берілген акустикалық сипаттамаға ие материалдардың қажетті құрылымдық құрамын болжауға мүмкіндік береді. Қазіргі уақытқа дейін, қазіргі заманғы қорытпалардың қатты денелерінің кристалдық торларындағы ультрадыбыстың жұтылу процестері, металдардың кристалдық торларындағы ультрадыбыстық жұтылу коэффициентінің температураға тәуелділігі толыққанды зерттелмеген. Көпқабатты конструкциялардың акустикалық сипаттамаларын есептеудің аналитикалық әдістері жоқ. Металдардың дыбыс өткізгіштігін есептеу қызығушылық тудыруда. Қатты денелердің кристалдарындағы ультра- және гипердыбыстық тербелістердің жұтылуы микродеңгейде зерттелуде. Мұнда фонондық және дислокациялық теория негізге алынады. Катты денелердегі ультра - және гипердыбыстардың дисперсиялары мена жытылуға байланысты мәселелер күрделі сипатқа ие. Қатты денелердің құрылымы түрліше болады; оларда өзара әсерлесетін серпімді толқындардың әртүрлі типтері таралуы мүмкін. Егер қатты дененің өлшемдері шектелген болса, онда көлемдіден басқа беттік толқындардың түрлі типтері пайда болады. Теориялық қарастыруға келетін ең қарапайым жағдай бұл изотропты, қатты диэлектрикте серпімді толқындардың ақаусыз және қоспасыз таралуы жөніндегі есеп. Формальды түрде, мұндай диэлектрикте дыбыстың жутылуы жөніндегі мәселені, диссипативті күштердің - ішкі үйкеліс (тұтқырлық) және жылуөткізгіштіктің әсерінен дыбыс энергиясының жоғалуын анықтау әдісіне негізделіп, феноменологиялық тұрғыдан қарастыруға болады. Бұл пікірден
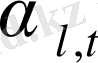 жазық, қума және көлденең, гармоникалық толқындардың жұтылу коэффициенттері үшін теңдеулер алуға болады. Мұндай әдіспен α жұтылу коэффициенті үшін алынған теңдеу, кейбір жағдайларда шаманың дұрыс реттілігін береді, дегенмен, бәрібір α эксперимент нәтижесімен сәйкес келмейді; әдетте α ның дыбыс жиілігі Ω (α~Ω
2
) ға тәуелділігі әсіресе, салыстырмалы жоғарғы ультрадыбыстық жиілікте және төменгі температурада расталмайды. Л. Д. Ландау және Ю. Б. Румер теория негізіне үш фононды әсерлесу жөніндегі ұғымды алды : дыбыс фононы, жылулық фононмен әсерлескенде жұтылады, нәтижесінде үшінші фонон пайда болады [1] . Кванттық-механикалық әдіске негізделген бұл теория Ωτ >> 1( мұндағы τ - жылулық фононның өмір сүру уақыты) жағдайына немесе дыбыс толқынының ұзындығы Λ, жылулық фононның еркін жүру жолының ұзындығы
жазық, қума және көлденең, гармоникалық толқындардың жұтылу коэффициенттері үшін теңдеулер алуға болады. Мұндай әдіспен α жұтылу коэффициенті үшін алынған теңдеу, кейбір жағдайларда шаманың дұрыс реттілігін береді, дегенмен, бәрібір α эксперимент нәтижесімен сәйкес келмейді; әдетте α ның дыбыс жиілігі Ω (α~Ω
2
) ға тәуелділігі әсіресе, салыстырмалы жоғарғы ультрадыбыстық жиілікте және төменгі температурада расталмайды. Л. Д. Ландау және Ю. Б. Румер теория негізіне үш фононды әсерлесу жөніндегі ұғымды алды : дыбыс фононы, жылулық фононмен әсерлескенде жұтылады, нәтижесінде үшінші фонон пайда болады [1] . Кванттық-механикалық әдіске негізделген бұл теория Ωτ >> 1( мұндағы τ - жылулық фононның өмір сүру уақыты) жағдайына немесе дыбыс толқынының ұзындығы Λ, жылулық фононның еркін жүру жолының ұзындығы
 тен едәуір аз болған жағдайына сәйкес келеді. Келесі шекті жағдай, Ωτ << 1 (салыстырмалы түрде төмен ультрадыбыстық жиіліктер және біршама жоғары (мысалы, бөлме) температуралар - А. И. Ахиезера жұмысында қарастырылған [1] . Бұл Больцманның кинетикалық теңдеуін пайдалану арқылы макроскопиялық тұрғыдан қарастыру болып табылады .
тен едәуір аз болған жағдайына сәйкес келеді. Келесі шекті жағдай, Ωτ << 1 (салыстырмалы түрде төмен ультрадыбыстық жиіліктер және біршама жоғары (мысалы, бөлме) температуралар - А. И. Ахиезера жұмысында қарастырылған [1] . Бұл Больцманның кинетикалық теңдеуін пайдалану арқылы макроскопиялық тұрғыдан қарастыру болып табылады .
Практикада радиолокациялық дабылдардың бөгелу желілерінде, фильтрлерде және радиодабылдарды өңдеудің әртүрлі элементтерінде кеңінен қолданылады.
Берілген жұмыста әртүрлі материалдармен конструкциялардың дыбыс жұтқыштық қасиеттері зерттелді. Алынған нәтижелер негізінде, конструкциялардың жасақталған дыбысжұтқыштығын пайдалану жөнінде кеңестер берілді. Қатты денелердің кристалдық торларының қатаңдық (дыбыс өткізгіштік) дәрежелерін есептеу нәтижелері келтірілген. Алюминий, темір, никель және басқа да атомдарының кристалдық торларындағы ультрадыбыстық жұтылу коэффициентінің әртүрлі жиілікте температураға тәуелділігі есептелді. Фонондық теория негізінде, дыбыс жұтқыштықты көтеру мақсатында, автоматтық болаттардағы ультрадыбыстық энергияның жұтылуы зерттелді. Болаттың диссипативтік параметрлерінің салыстырмалы түрдегі ең жоғарғы мәндерін құрамындағы көміртегі және кремний көрсетті. Дыбыстың жұту коэффициентін білу, көлемді және жұқа қабаттардағы дыбыс қысымының таралуы сияқты өзекті мәселелерін қарастыруға мүмкіндік берді.
Кристалдық торлардағы ультрадыбыстық жұтуды зерттеудің нәтижелерін, радиолокациялық дабылдардың бөгелу желілерінде, фильтрлерде және радиодабылдарды өңдеудің әртүрлі элементтерінде, транзисторларды құрастырғанда және т. б. қолдануға болады.
1. Теориялық бөлім
1. 1 Конденсирленген орталардағы дыбыс жұтылуының қысқаша теориясы.
Жалпы жағдайда дыбыс жұту коэффициентін мына түрде жазуға болады :
α =
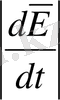 /2c
/2c
 ,
,
 үшін
үшін
 = ρ
= ρ
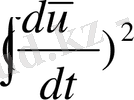 dV, (1. 1)
dV, (1. 1)
мұнда гармоникалық қума толқынды қарастырғанда u = u
x
= u
0
cos (kx - Ωt), u = u
x
= 0 - х осі бағытымен таралатын толқындағы ығысу. Қума және көлденең толқындар үшін дыбыс жұту коэффициенттері α
 α
t
бір-бірінен ерекше болуы тиіс. Қума толқында дефромация бұл изотроптық сығылу мен ығысудың қиысыуы болса, көлденең толқында тек ығысу болады. Осыған сәйкес, қума толқында ішкі үйкеліс немесе тұтқырлық есебінен болатын жұтылудан басқа сығылу және сирету аймағында температураның теңесуі жүруі мүмкін. Демек, ішкі шығынға жылу өткізгіштікке
α
t
бір-бірінен ерекше болуы тиіс. Қума толқында дефромация бұл изотроптық сығылу мен ығысудың қиысыуы болса, көлденең толқында тек ығысу болады. Осыған сәйкес, қума толқында ішкі үйкеліс немесе тұтқырлық есебінен болатын жұтылудан басқа сығылу және сирету аймағында температураның теңесуі жүруі мүмкін. Демек, ішкі шығынға жылу өткізгіштікке
 ге кеткен шығын қосылады. . Сонымен, α
t
тек η функциясы болғанда, жұту коэффициенті α
ге кеткен шығын қосылады. . Сонымен, α
t
тек η функциясы болғанда, жұту коэффициенті α
 η, η
!
және
η, η
!
және
 функциясы болады (Ескерту, мұндағы
функциясы болады (Ескерту, мұндағы
 - жылуөткізгіштік коэффициенті) ;
- жылуөткізгіштік коэффициенті) ;
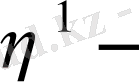 көлемді тұтқырлық (көлемді кеңею немесе сығылу) ;
көлемді тұтқырлық (көлемді кеңею немесе сығылу) ;
 - ығысу тұтқырлығы [Па·с] ) .
- ығысу тұтқырлығы [Па·с] ) .
Термодинамика жағдайларына сәйкес,
 = -
= -
 = - T
= - T
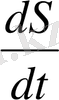 Equation. 3 . (1. 2)
Equation. 3 . (1. 2)
Изотропты дене қарастыра отырып:
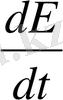 = -
= -
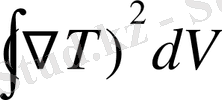 - 2η
- 2η
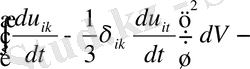
 , (1. 3)
, (1. 3)
Енді
 Т =
Т =
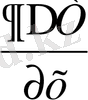 - температура өзгерісінің градиентін табайық
- температура өзгерісінің градиентін табайық
 = Т - Т
0
.
= Т - Т
0
.
Дыбыстың таралуындағы адиабаттық шартына сәйкес, деформация тензоры бірінші реттіліктегі мүшелерге дейін дәл болады
S(T
0
) = S(T) + Kβu
 Equation. 3 . (1. 4)
Equation. 3 . (1. 4)
мұндағы T
0
қандайда бір берілген температура, Т дене температурасы және ол T
0
ден сәл-ақ озгеше; β - жылулықтың кеңею коэффициенті. Мұндай нәтижеге температураның өзгерісін ескере отырып, дененің деформациясын қарастырғанда, дененің ішкі энергиясында тағыда бір мүшені Kβ(Т-Т
0
) u
 Equation. 3 ескеру арқылы қол жеткіземіз, (4) теңдеуде К шамасы - көлемді және жан-жақтан сығылу модулі (көлемді серпімділік модулі) болып табылады, ол
Ķ
сығылумен келесі қатынас арқылы байланысқан
Ķ
= К
-1
.
Equation. 3 ескеру арқылы қол жеткіземіз, (4) теңдеуде К шамасы - көлемді және жан-жақтан сығылу модулі (көлемді серпімділік модулі) болып табылады, ол
Ķ
сығылумен келесі қатынас арқылы байланысқан
Ķ
= К
-1
.
Сығылу және сиретілу аймақтарында
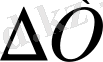 температура айырымы аз болған жағдайда S(T) - S(T
0
) айырымын қатарға жіктеуге болады. Дәлдігі бойынша бірінші реттіліктегі мүшелерге дейін
температура айырымы аз болған жағдайда S(T) - S(T
0
) айырымын қатарға жіктеуге болады. Дәлдігі бойынша бірінші реттіліктегі мүшелерге дейін
S(T) - S(T
0
) = (Т - Т
0
)
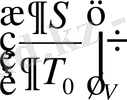 Equation. 3 =
Equation. 3 =
 Equation. 3 (Т - Т
0
) , (1. 5)
Equation. 3 (Т - Т
0
) , (1. 5)
Бұдан
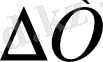 Equation. 3 = Т - Т
0
= -
Equation. 3 = Т - Т
0
= -
 Equation. 3 u
ii .
Equation. 3 u
ii .
Қума толқындардың жылдамдығы с
 Equation. 3 келесі түрде анықталады
Equation. 3 келесі түрде анықталады
с
 =
=
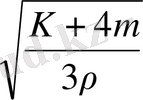 ,
,
мұндағы μ =
 - ығысу модулі,
- ығысу модулі,
 - Пуассона коэффициенті.
- Пуассона коэффициенті.
Сонда
К =
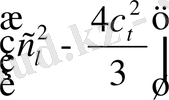 ρ, (1. 6)
ρ, (1. 6)
және
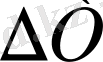 = - (Тβρ/C
P
) (
= - (Тβρ/C
P
) (
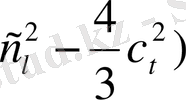 . (1, 7)
. (1, 7)
Адиабаттық К, изотермиялық К из және жан-жақты сығылу модулі келесі қатынас арқылы байланысады [1] :
К
из
=
 К . (1. 8)
К . (1. 8)
Және бір-бірінен озгешеленеді.
Қатты диэлектриктер үшін С
V
≈ C
P
≈ C
P
.
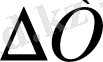 анықтау арқылы, (2) теңдеудегі бірінші мүшені есептеуге болады, онда
анықтау арқылы, (2) теңдеудегі бірінші мүшені есептеуге болады, онда
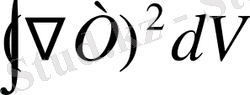 =
=
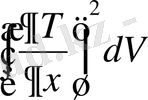 . (1. 9)
. (1. 9)
Енди u
x
(x, t) ке арналған теңдеуді қолданып және дыбыс периоды бойынша орташалап, (1) теңдеуге сәйкес
 ні, ал (9) және (3) теңдеулер арқылы
ні, ал (9) және (3) теңдеулер арқылы
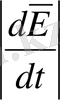 табамыз. Осы есптеулер нәтижесінде келесіге келеміз:
табамыз. Осы есптеулер нәтижесінде келесіге келеміз:
α
 =
=
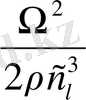
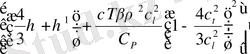 .
(1. 10)
.
(1. 10)
х осі бойымен таралатын көлденең толқындар үшін толқындағы ығысу u x = 0 u y = u yo cos(kx-Ωt), u z = u zo cos(kx-Ωt) болады, және u ik деформация тензорындағы компоненттер нолге тең болмайды:
u xy = - ½ u oy ksin(kx-Ωt), u xz ksin(kx-Ωt), (1. 11)
Көлденең толқындар үшін есептеулерден келесіні аламыз
α t = ηΩ 2 / 2ρc t 2 . (1. 12)
[6] жұмыста анизотропты диэлектриктердегі дыбыстың жұтылуы осылай қарастырылған.
Қатты денелер акустикасында изотропты диэлектриктер үшін α
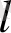 және α
t
үшін жазылған теңдеулер экспериментпен барлық уақытта сәйкес келе бермейді. α ның жиілікке квадраттық түрдегі тәуелділігі де расталмаған. Жоғарғы жиіліктерде кейбір диэлектриктер үшін α(Ω) сызықтық тәуелділігі байқалады. Төменгі жиіліктерде Ω ға тәуелділік тіпті болмауы да мүмкін. Диэлекриктерден басқа металдар мен жартылай өткізгіштерге жасалған қорытындыларда ерекше сақтық талап етіледі. α мінезіндегі теориядан ауытқушылықтар бір жағынан қатты денелердің берілген үлгілерінің көптігімен түсіндірілсе (диэлектриктер, металдар, жартылайөткізгіштер, кристалдар және аморфтық денелер), екінші жағынан оларды алу жолы (құйу, балқу, кристалдану), кристалдардағы қоспалардың, дислокация мен ақаулардың, сонымен қатар құрамдарының күрделі (металдардың қорытпалары) болуымен түсіндіруге болады. Физикалық шамалар кестесінде қатты денелер үшін η және η
1
мәндері келтірілмеген; ішкі үйкеліс бойынша ғана мағлумат бар
.
Негізінен ішкі үйкеліс пен тұтқырлық арасында байланыс бар.
және α
t
үшін жазылған теңдеулер экспериментпен барлық уақытта сәйкес келе бермейді. α ның жиілікке квадраттық түрдегі тәуелділігі де расталмаған. Жоғарғы жиіліктерде кейбір диэлектриктер үшін α(Ω) сызықтық тәуелділігі байқалады. Төменгі жиіліктерде Ω ға тәуелділік тіпті болмауы да мүмкін. Диэлекриктерден басқа металдар мен жартылай өткізгіштерге жасалған қорытындыларда ерекше сақтық талап етіледі. α мінезіндегі теориядан ауытқушылықтар бір жағынан қатты денелердің берілген үлгілерінің көптігімен түсіндірілсе (диэлектриктер, металдар, жартылайөткізгіштер, кристалдар және аморфтық денелер), екінші жағынан оларды алу жолы (құйу, балқу, кристалдану), кристалдардағы қоспалардың, дислокация мен ақаулардың, сонымен қатар құрамдарының күрделі (металдардың қорытпалары) болуымен түсіндіруге болады. Физикалық шамалар кестесінде қатты денелер үшін η және η
1
мәндері келтірілмеген; ішкі үйкеліс бойынша ғана мағлумат бар
.
Негізінен ішкі үйкеліс пен тұтқырлық арасында байланыс бар.
Беттік Релей толқындары құрылымы жағынан біртексіз қума және көлденең толқындардың қисындасуы болып табылады. Онда сол толқын ұзындықтағы аз шығынға ие серпімді ортадағы
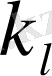 ,
,

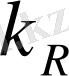 толқындық сандарды келесі түрде жазуға болады [1, 2] :
толқындық сандарды келесі түрде жазуға болады [1, 2] :
 =
=
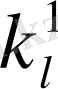 +
+
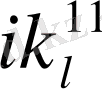 =
=
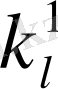 (1 +
(1 +
 )
)
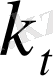 =
=
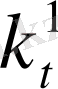 +
+
 =
=
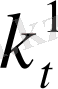 (1 +
(1 +
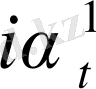 ) (1. 13)
) (1. 13)
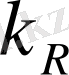 =
=
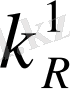 +
+
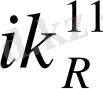 =
=
 (1 +
(1 +
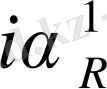 ),
),
где
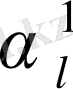 =
=
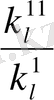 ,
,
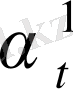 =
=
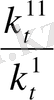 ,
,
 =
=
 - өте аз түзетулер, олар сандық жағынан толқын ұзындықтағы өшу коэффициенттерін 2π ге бөлгенге тең.
- өте аз түзетулер, олар сандық жағынан толқын ұзындықтағы өшу коэффициенттерін 2π ге бөлгенге тең.
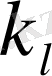 ,
,
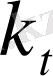 ,
,
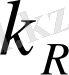 мәндерін Релейдің сипаттық теңдеуіне қою арқылы келесі трдегі теңдеуді аламыз [8] :
мәндерін Релейдің сипаттық теңдеуіне қою арқылы келесі трдегі теңдеуді аламыз [8] :
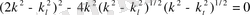 . (1. 14)
. (1. 14)
Шын және жорымал жақтарын нолге теңестіре отырып,
 және
және
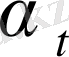 қисындасуы арқылы алынған α
R
Релей толқынының жұту коэффициенті үшін теңдеуді аламыз. Әдетте α
R
қума толқынның жұтылу коэффициенті
қисындасуы арқылы алынған α
R
Релей толқынының жұту коэффициенті үшін теңдеуді аламыз. Әдетте α
R
қума толқынның жұтылу коэффициенті
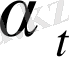 мен салыстырғанда бірнеше есе көп болады.
мен салыстырғанда бірнеше есе көп болады.
1. 2 Кристалдық тордың тербелістері және фонондар
Идеал ақаусыз диэлектриктік кристалдағы тордың динамикасын қарастырайық.
Қатты денедегі жылулық қозғалыс - бұл фонондар деп аталатын квазибөлшектік газ түрінде сипаттауға ыңғайлы болатын, атомдардың өз тепе-теңдігіне салыстырғандағы тербелісі. Жылулық фонондар немесе әрқайсысы энергиясы ħω (ω - жылулық фононның жиілігі) және квазиимпульсы ħк (к - толқындық вектор) серпімді жазық гармоникалық толқын болатын Дебай кванттары энергияның немесе жиіліктің кері спектріне ие (кейде оны фонондық спектр деп те атайды) .
Фонондардың ең кіші жиілігі немесе сәйкесінше серпімді толқындардың ең үлкен толқын ұзындықтары үлгінің өлшемімен, ең жоғарғы жиілік- көршілес атомдардың арақашықтығымен (тор параметрі а арқылы) анықталады.
λ ~ а (λ - жылулық фононның толқын ұзындығы) болған жағдайда фонондық спектр үзіледі. 1. 1 - суретте Дебайдың жылусыйымдылық теориясынан шығатын Z(ω) фонондарының спектрі (штрихталған қисық) және Li үшін алынған эксперименталдық қисық [3] (тұтас қисық) . Эксперименталдық қисықтың баяу емес жүруі кристалдың анизотропиясын ескермегендіктен болады.
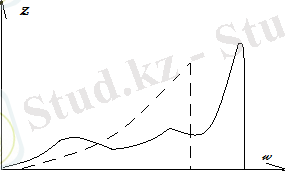
1. 1 - сурет - Идеалдандырылған Дебай спектрі (немесе фонондық күйлердің тығыздығы) (штрих) және спектр Li [9] үшін, эксперименттен алынған
1. 2 - суретте жылулық, серпімді толқынның ұзындығы үлгі өлшеміне (үлгі-Х-45 0 кесілген сегнет тұзы кристалының кесегі) жақынырақ болатын, яғни 4, 7х0, 5х0, 7 см 2 өлшемдерге жақын спектрдің төменгі жиіліктегі тордың жылулық тербелісі көрсетілген [4] . Үлгідегі Дебайдың қума толқындары пьезоэлектриктік эффектіге сәйкес, оның метал астарларында V айнымалы кернеуін пайда етеді. Сонымен, осы толқындардың f спектрі электр жағында шығарылады.
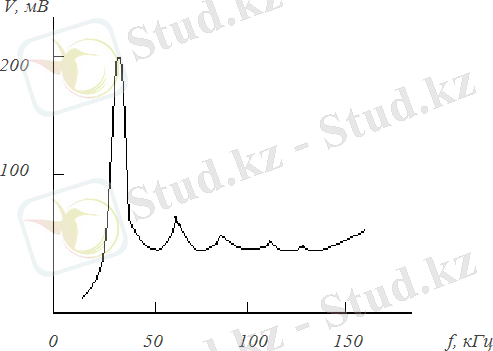
1. 2 - сурет - Спектрдың төменгі жиілігіндегі тордың жылулық тербелістері
Дебайдың негізгі болжамы бойынша, серпімді спектр ω max = ω D жиілікте үзіледі. Онда ω ның к дан сызықтық тәуелділігін жоғарғы жиіліктерге шамалап экстраполяциялауға және Планк теңдеуіне сәйкес осцилляторларды жиіліктер бойынша жіктеуге болады. N атом үшін кристал торында 3N осцилляторлар болғандықтан (еркіндік дәрежесі), фонондардың спектрі жалпы осцилляторлар саны 3N болатындай ω D Дебай жиілігімен шектелуі тиіс, яғни
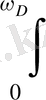 Z(ω) dω = 3N. (1. 15)
Z(ω) dω = 3N. (1. 15)
мұндағы Z(ω) - dω аралығындағы осцилляторлар саны. (По теории Дебай теориясына сәйкес кристалдың қарапайым ұяшығында бір атом болады) .
Дебайдың сипаттауыш температурасы θ D келесі өрнектен анықталады
ħω D = k Б θ D . (1. 16)
мұнда k Б - Больцман тұрақтысы.
Дебай температурасы θ D - кристалдың қатаңдық және дыбыс өткізгіштік дәрежесін сипаттайды. θ D қаншалықты үлкен болса, кристалл дыбысты сонша жақсы өткізеді. [5] есептеуден кварц үшін θ D ≈ 400К ≈ 400К, ал қорғасын үшін θ D ≈ 100К. «Сызықты тәуелділік» θ D ға байланысты өседі .
Екі атомдық кристалдың тербелісі (ұяшығында массалары әртүрлі m және M болатын екі атомы бар) екі тербеліс тармағынан немесе модалардан тұрады. Ең жоғарғы жиіліктілер оптикалық тармақтар (қума толқындар үшін оларды LO деп, ал көлденең толқындар үшін -ТО деп белгілейді) . Опти калық тармақтарда, m және M массалы тербелістегі атомдар к≈0 болған жағдайда, бір-біріне қатысты, массалары бірдей атомдар арасында өзгермейтін қашықтыққа ығысады.
Тербеліс кезінде бірдей атомдардың арақашықтығы озгеретін болса, мұндай тербелістер төменгі жиілікті (нөлдік жиіліктен бастап) болады және акустикалық тармақтар деп аталады (LА - қума, ТА - көлденең акустикалық тармақ) . Акустикалық Дебай тербелістері - оптикалық тербелістер (к≈0) ауырлық центрі қозғалмайтын, ұяшықтар ішіндегі деформацияға жауапты кездегі қарапайым ұяшықтың бүтіндей ығысуы. 1. 3 - суретте ω ның k дан эксперименттік тәуелділігі келтірілген (дисперсиялық қисық) [1] . Өлшеулер (NaFl 7 ) натрий флуоридінде Т=219К төменгі температурада баяу нейтрондарды шашырату әдісімен жүргізілді.
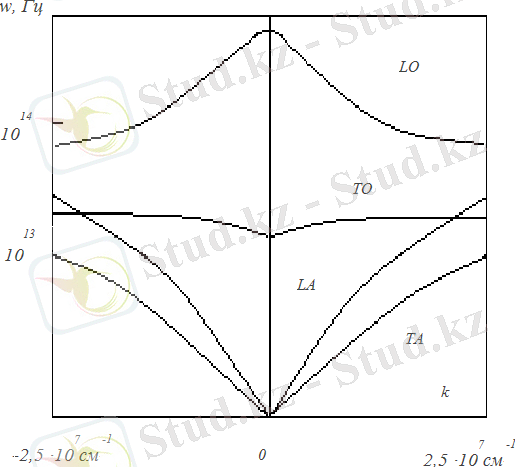
1. 3- сурет - Натрий флуоридінде таралатын фонондар үшін дисперсиялық қисық [9] . Екі көлденең акустикалық тармақ [100] бағытына сәйкес келеді
1. 3 - суреттен акустикалық және оптикалық тармақтардың дисперсияға ие екендігі көрініп тұр. Акустикалық тармақтар үшін к нолге жақын болғанда ω және k арасында тура пропорционалдық орнайды. k ≈ 2∙10 7 см -1 болғанда акустикалық және оптикалық тармақтар қиылысады. Бірнеше ұяшықтардан тұратын күрделі ұяшықтар үшін ТО - және LА - тербелістерінің қиылысу аймағы кішкентай k үшін нақты айқындалған болады. TiO 2 типпіндегі қарапайым кристалдар үшін акустикалық және оптикалық фонондардың рухсат етілген зоналары жиіліктің кең интервалында қиылысады. Бұл әсер оптикалық тербеліс α ға өз үлесін қосатындықтан, дыбыс жұту теориясында үлкен маңызға ие [5] .
Жылуөткізгіштік, қатты денелердің жылулық кеңейуі және дыбыстың жұтылуы сияқты коллективті кинетикалық құбылысты дұрыс түсіндіру үшін тордың қалыпты жылулық тебелісінің әсерлеспейтін фонондардың газдары сияқты көрінісі жеткіліксіз болады екен. Мұны түсіндіру үшін қатты денелер физикасында фонон-фонондық әсерлесу процестері ескеріледі - фонондар бір-бірімен серпімсіз соқтығысуы; екі фонон соқтығысқанда үшінші фононның туылуы (қосылу прцесі) немесе керісінше, фонон екі фононға ыдырауы (ыдырау процесі) . Үш фонондық және төрт фонондық процестердің диаграммалары болуы мүмкін. Төрт фонондық процесс төртінші модульдер мен сәйкес келеді.
1. 3 Кристалдардың жылулық қасиеттері
Бөлме температурасында кристалдағы атомдардың тербеліс амплитудасы шамамен 0, 1 атомдық аралықты құрайды, яғни ( 0, 1-0, 2)
 шамасына. Атомдардың жылулық тербелісінің амплитудасының қатаң тұрақты бағыты болмайды - бұл көршілес атомдармен байланысы арқылы анықталатын күрделі тербеліс.
шамасына. Атомдардың жылулық тербелісінің амплитудасының қатаң тұрақты бағыты болмайды - бұл көршілес атомдармен байланысы арқылы анықталатын күрделі тербеліс.
Бұл байланыстар бағытталған болғандықтан, тербелістер анизотропты болады, ал ол өз кезегінде, монокристалдың сызықтық ұлғаю коэффициентінің анизотроптылығына алып келеді. Ескеретін жағдай, дененің қыздырғанда кеңеюі тербеліс амплитудасының өсу фактісінен шықпайды. Кеңейю тербелетін дененің энергиясының өсуімен түсіндіріледі.
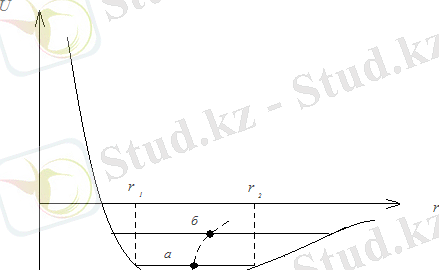
1. 4 - сурет - Сызықтық тізбектің атомдарының өзара әсерлесуінің потенциалдық энергиясы U(x) . Тепе-теңдік жағдай, шамамен қисықтың минимумы арқылы анықталады
1. 4 - суреттегі а горизонтал түзу, қандайда бір температурада (мысалы, бөлме) кристалдық тордағы атом энергиясының деңгейін көрсетеді. Бұл түзудің энергия қисығымен түйісу нүктесі, сол тордағы атом тербелген кездегі соңғы r 1 және r 2 орнын анықтайды. Түзудің ортасы, берілген температурада атомның тепе-теңдік жағдайын анықтайды. Температура жоғарылаған кезде атом б түзуімен анықталатын жоғарғы энергетикалық деңгейге ауысады. б түзуінің ұзындығы а түзуінің ұзындығына қарағанда ұзын болады, ал ол атом тербелісінің амплитудасының өскенін білдіреді. Энергия қисығының симметриялы еместігінен, б түзуі оңға ығысқанын, яғни атомның тепе-теңдік күйінен ығысқанын білдіреді: атомдар арсындағы қашықтық өсіп, кристалды қыздырғанда кеңеюіне алып келеді. Демек, қыздырғанда, дененің сызықтық өлшемдерінің өсуі, тербеліс амплитудасының өскенінен емес, тепе-теңдік күйін сипаттайтын атом арасындағы аралықтың өсуімен түсіндіріледі.
Кеңею анизотропиясына байланысты әртүрлі кристаллографиялық бағыттарының бойындағы кристалдың сызықтық ұлғаю коэффициенті өзара ерекшеленіп тұрады. Кристалдағы атомдар арасындағы байланыс атомдар тобының тербелісіне алып келеді. Кристалл - бұл өлшемдеріне шектеу қойылған дене, мұндай денедегі тербелістер тұрғын толқындардың пайда болуына алып келеді. Тұрғын толқындардың ең үлкен ұзындығы түгел кристалдың тербелісіне сәйкес келеді. Оның ұзындығы бойынша тұрғын толқын анықталады. 2
 = λ. Бірақ, кристал бүтін біртұтас болып тербеліп қана қоймай, молекуласындағы жеке атомдардың тербелісі анықталады. Кристалда еркіндік дәрежесі қанша болса, сонша тұрғын толқын анықталады. N атомнан құралған қатты дененің 3N еркіндік дәрежесі болады. Сонымен қатар, молекула кристалындағы молекула құрайтын бірнеше атомдар тобы еркіндік дәрежесінің жалпы санын көбейте отырып, бүтін біртұтас ретінде тербеледі. Мұндай заттарда айналмалы еркіндік дәрежесі де болады. Егер атомдардың мұндай тобын n деп белгілесек, ондақатты денелердегі мүмкін болатын тұрғын толқындар саны 3nN. Осы толқындардың беттесуі кристалдағы жылулық қозғалысты құрайды. Ең ұзын толқын дене өлшемімен анықталады λ
1
= 2
= λ. Бірақ, кристал бүтін біртұтас болып тербеліп қана қоймай, молекуласындағы жеке атомдардың тербелісі анықталады. Кристалда еркіндік дәрежесі қанша болса, сонша тұрғын толқын анықталады. N атомнан құралған қатты дененің 3N еркіндік дәрежесі болады. Сонымен қатар, молекула кристалындағы молекула құрайтын бірнеше атомдар тобы еркіндік дәрежесінің жалпы санын көбейте отырып, бүтін біртұтас ретінде тербеледі. Мұндай заттарда айналмалы еркіндік дәрежесі де болады. Егер атомдардың мұндай тобын n деп белгілесек, ондақатты денелердегі мүмкін болатын тұрғын толқындар саны 3nN. Осы толқындардың беттесуі кристалдағы жылулық қозғалысты құрайды. Ең ұзын толқын дене өлшемімен анықталады λ
1
= 2
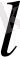 . Ол акустикалық толқын деп аталады, ең қысқа ұзындық атомдық тордың d периодымен анықталады, λ
2
= 2d. Жеке атомдар мен атомдардың топтарының тербелістері арқылы пайда болған тұрғын толқындар оптикалық деп аталады.
. Ол акустикалық толқын деп аталады, ең қысқа ұзындық атомдық тордың d периодымен анықталады, λ
2
= 2d. Жеке атомдар мен атомдардың топтарының тербелістері арқылы пайда болған тұрғын толқындар оптикалық деп аталады.
Фонондар металдардағы электрондармен бірдей қатты дененің жылу өткізгіштігін жүзеге асырады. Фонондар қатты денелердегі серпімді тербелістің түрі ретінде болғандықтан, олардың таралу жылдамдықтары серпімді толқынның таралу жылдамдығына, яғни дыбыс жылдамдығына тең болуы керек, ал ол қатты денеде көп жылу өткізуі керек. Бірақ фонондар жоғарыда айтылғандай, басқа фонондармен және ақаулармен көп соқтығысып, шашырайды, сондықтан олардың таралу жылдамдығы өте аз болады.
Фононның еркін жүруі шекаралық бетпен және кристал біртектілігімен және фонондардың өзара соқтығысуымен шектелген.
Фононның еркін жүру жолы
 жоғарғы температурада л т 1/T, төменгі температурада -
жоғарғы температурада л т 1/T, төменгі температурада -
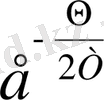 шамасына пропорционал, мұнда θ - сипаттауыш температура.
шамасына пропорционал, мұнда θ - сипаттауыш температура.
Метал емес кристалдардың жылуөткізгіштігі фононның еркін жүру жолына пропорционал, онда кристалдың жылуөткізгіштік коэффициенті
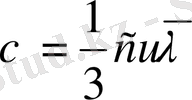 , (1. 17)
, (1. 17)
С - бірлік көлемдегі жылусыйымдылық, u - дыбыс жылдамдығы; с - фонондардың орташа жылдамдығы.
Кристалдың жылуөткізгіштігі үшін Фурье теңдеуі
Q =
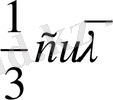 St
St
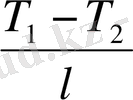 . (1. 18)
. (1. 18)
S - жылулық ағын бағытына перпендикуляр болатын кристалдың қимасынынң ауданы, t - уақыт,
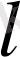 - кристал ұзындығы; Т
1
- Т
2
- температуралар айырымы.
- кристал ұзындығы; Т
1
- Т
2
- температуралар айырымы.
Жылу алмасуда электрондардың болуы себепті металдық кристалдардың жылуөткізгіштігі бір, екі ретке көп.
Екінші жағынан дыбыс жиілігін келесі теңдеу түрінде көрсетуге болатындықтан [5] :
Ω «
 ≈к
Б
Т/ħ . (1. 19)
≈к
Б
Т/ħ . (1. 19)
 - жылулық фонондардың жиілігінің орташа мәні.
- жылулық фонондардың жиілігінің орташа мәні.
Жылуөткізгіштік теңдеуін былай жазуға болады
 . (1. 20)
. (1. 20)
с - фонондардың орташа жылдамдығы, С - тордың жылусыйымдылығы, τ - жылулық фонондардың орташа өмір сүру уақыты.
Жылулық фонондар тепе-теңдік күйде Бозе - Эйнштейн статистикасына бағынады. толқындық векторы к 1 және поляризациясы J 1 болатын фонондардың таралу функциясы n 1 келесі түрде болады
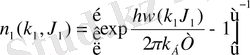 . (1. 21)
. (1. 21)
Жылулық фонондардың жиілікткрінің орташа мәні келесі теңдеуден анықталады
ħ
 ≈ к
Б
Т (1. 22)
≈ к
Б
Т (1. 22)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz