ФУНКЦИОНАЛДЫ ТАЛДАУДАҒЫ СЫЗЫҚТЫ ОПЕРАТОРЛАР ТЕОРИЯСЫ

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 64 бет
Таңдаулыға:

МАЗМҰНЫ

КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 4

1. ОПЕРАТОРЛЫҚ ЕСЕПТЕУЛЕРДЕГІ ЛАПЛАС ТҮРЛЕНДІРУІ
1.1 Лаплас түрлендіруі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 6
1.2 Лаплас түрлендіруінің қасиеттері ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... 13
1.3 Шектік есептерді шешудің вариациялық әдістері ... ... ... ... ... ... ... ... ... ... ...17

2. ФУНКЦИОНАЛДЫ ТАЛДАУДАҒЫ СЫЗЫҚТЫ ОПЕРАТОРЛАР ТЕОРИЯСЫ
2.1 Lp кеңістігі және сызықтық оператор ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..2 6
2.2 Сызықтық емес Урысон интегралдық операторының кейбір қасиеттері ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..31
2.3 Урысон операторының бір классының үзіліссіздік критерийлері ... ... ... ... 35
2.4 Матрица және оның негізгі ұғымдары ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .39
2.5 Квадраттық форма және оны түрлендіру ... ... ... ... ... ... . ... ... ... ... ... ... ... ...50

3. ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕРДІ ШЕШУДЕ ОПЕРАТОРЛЫҚ ӘДІСТЕРДІ ҚОЛДАНУ
3.1 Коэффициенттері тұрақты сызықтық дифференциалдық теңдеулерді операторлық әдіспен шешу ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..60
3.2 Сызықтық дифференциалдық теңдеуді Дюамель интегралын пайдаланып шешу ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 63
3.3 Коэффициенттері тұрақты сызықтық дифференциалдық теңдеулер жүйесін операторлық әдіспен шешу ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..66
3.4 Операторлық әдістерді пайдаланып меншіксіз интегралдарды есептеу мысалдары ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 68

ҚОРЫТЫНДЫ ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .71

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ ... ... ... ... ... ... ... . ... ... ... ... ... ... ..73

КІРІСПЕ

Ел дамуының ертеңгі бағыт- бағдарын саралаған Елбасының Жолдауында білім беру саласына: Ұлттық бәсекелестік қабілеті бірінші кезекте оның білімділік деңгейімен айқындалады. Әлемдік білім кеңістігіне толығымен кірігу білім беру жүйесін халықаралық деңгейге көтеруді талап ететіні сөзсіз деп ерекше мән берілген. Алайда, жаһандану дәуірінде қатаң бәсекеге төтеп бере алатын мемлекет қана өркениет көшіне ілесе алады. Мемлекеттің бәсекелестік қабілеті ең алдымен оның білімділік сипатымен айқындалатынын ескере келе, білім мен тәрбие беру саласының маңызы ерекше екенін мойындауымыз керек.
Адам қазіргі дамуында табиғаты мен ойының мөлшерсіз мүмкіндіктерін игеруге ұмтылуы қажет. Қазіргі таңда мұғалімдердің негізгі міндеті - ұлттық ділі жоғары, сана-сезімі дамыған, өзіндік көзқарасы бар жеке тұлғаны қалыптастыру және оқушылардың өз бетімен білім алу жолдарына үйрету.
Осыған орай оқушы оқыту үрдісінде, әрбір сабақта өзінің оқу әрекетінің мақсат-міндеттерін анықтап, соларды іске асырудың нақты тәсілдерімен амалдарын қолданып, өзін-өзі бақылап отыруға тиіс. Міне, осындай жағдайда ғана балада білімге деген қажеттілік, талпыныс, қызығу, танымдық белсенділігі қалыптасады.
Оқушыны оқу үрдісінің нысаны ретінде ғана санамай, оны сол үрдістің тең құқықты мүшесі ретінде қабылдап, оқушыға бет бұру қазіргі мектеп дамуының негізгі қарқынының бірі болып отыр. Қазақстан Республикасы гуманитарлық білім беру тұжырымдамасында білім берудің гуманитарлық сипаты, онда адам тек жай зерттеу объектісі ретінде ғана емес, ең алдымен, шығармашылық пен таным субъектісі, өзінің шығармашылыққа деген құлшынысымен оқушыларды баурап әкететін субъект ретінде көрінумен бедерленеді делінген. Осыдан білім беру саласында ең алғашқы орында тұрған ол-мектеп мәселесі екенін аңғара аламыз. Себебі мектеп бүкіл білім жүйесінің бастау алар тұсы, білімділіктің іргетасы қаланар сынақ алаңы.
Тақырыптың өзектілігі. Операторлық есептеу математикалық талдаудың маңызды бір саласы болып табылады. Механика, математика және техника есептерін шешуде операторлық әдістер жиі қолданылады. Жылу өткізгіштік теориясында, электротехника және радиотехника, электр тізбегіндегі тұрақты емес құбылыстарды,автоматты реттегіштер жүйесінің жұмысын зерттеуде, сонымен қатар сызықтық дифференциалдық және интегралдық, айырымдық теңдеулер теориясында операторлық есептеу әдістері кеңінен пайдаланылады.
Оператор, операция сөздері латын тілінде operor-жасаймын, operator-жасаушы, жұмыскер деген ұғымды білдіреді. Ал operatio-амал, қимыл, жұмыс, енгізу, іске асыру ұғымдарына сәйкес келеді.
Операторлық есептеу саласындағы алғашқы ғылыми жұмыстар белгілерді есептеу, белгілеулер енгізу арқылы есептеу деген сияқты атаулармен басталады. Операторлық әдістерді физикалық және техникалық есептерді шешу үшін қолдану ағылшын ғалымы Хевисайдтың 1892 жылы жарияланған еңбектерінен кейін басталған.
Операторлық есептеудің алғашқы математикалық түрде негізді дәлелденуі ағылшын математигі Бромвичтің (1916), америка инженері Карсонның (1926) және голландия инженер-электригі Ван дер Польдің (1929-1932) еңбектерімен тығыз байланысты. Россияда бұл саладағы алғашқы еңбектердің бірі М.Е. Ващенко-Захарченконың 1862 жылы шыққан монографиясы болып табылады. Операторлық есептеу теориясын дамытуда орыс ғалымдары Лурье А.И., Данилевский А.Н., Эфрос А.М., Конторович М.И., Диткин В.А. айтарлықтай үлес қосты.
Диплом жұмысының мақсаты математиканы оқытудағы операторлық есептердің маңызын көрсету болып табылады.
Дипломдық жұмыстың міндеттері:
- математикадағы сызықты операторлар мен операторлық есептерге шолу жасай;
- математикадағы функционалдық талдау ұғымына сипаттама беру;
- функционалдық талдаудағы сызықты операторлар теориясына анықтама беру.
Диплом жұмысының зерттеу нысаны сызықты алгебра болып табылады.
Диплом жұмысын жазу барысында есептеу, анықтама беру, мысалдар келтіру және дәлелде секілді математикалық тәсілдер қолданылды.
Диплом жұмысының құрылымы кіріспеден, үш бөлімнен, қорытындыдан және пайдаланылған әдебиеттер тізімінен тұрады.

1. ОПЕРАТОРЛЫҚ ЕСЕПТЕУЛЕРДЕГІ ЛАПЛАС ТҮРЛЕНДІРУІ
1.1 Лаплас түрлендіруі

Ғылыми зерттеулер нәтижесінде операторлық есептеу теориясында Лаплас бойынша түрлендірілетін функцияларды ғана пайдалану, оның қолданылу өрісін тарылтатындығы байқалды. Бұл кемшіліктен құтылу үшін Хевисайдтың белгілеулеріне қайта оралып, функция ұғымын жалпылау қажеттігі туды. Осындай қажеттілікпен байланысты жарыққа шыққан польша математигі Я. Микусинскийдің Операторлық есептеу деп аталатын еңбегі алғашқы операторлық көзқарасқа қайта оралудың бастамасы болды.
Операторлық әдістің мәнін қысқаша былай сипаттауға болады:
Нақты айнымалы t-ның 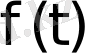функциясы берілсін дейік. Бұл функцияның Лаплас түрлендіруі (-түрлендіру) мына түрде болсын

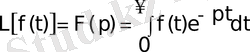
Бұл теңдіктің оң жағындағы жинақталатын меншіксіз интеграл.
түрлендіруін пайдаланып әрбір Лаплас бойынша түрлендірілетін түпнұсқа деп аталатын 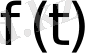функциясына оның бейнесі деп аталатын комплекс айнымалының 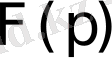функциясын сәйкес келтіруге болады.
Лаплас түрлендіруінің тамаша қасиеттері бар. Мысалы, 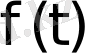түпнұсқасын бойынша дифференциалдауға 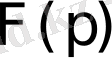функциясын р комплекс айнымалысына көбейту амалы сәйкес келеді. Сонымен, түпнұсқаны дифференциалдау және интегралдау амалдарына бейнелер кеңістігінде қарапайым алгебралық амалдар, яғни 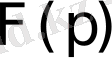бейнесін р санына көбейту және бөлу амалдары сәйкес келеді.
Берілген 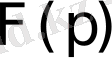бейнесі бойынша оған сәйкес 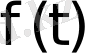түпнұсқасын табу үшін Лапластың кері түрлендіруін ( 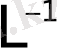түрлендіру) пайдалануға болады. Нақты айнымалы t-ның 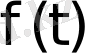функциясы үшін мына шарттар орындалсын:
1) Айнымалы t-ның мәндерінде функция мәні 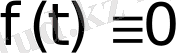болсын;
2) Нақты айнымалы t-ның 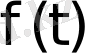функциясы барлық 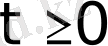мәндерінде үздіксіз болсын.
Үздіксіздік шарты тек бірінші текті үзіліс нүктелерінде ғана орындалмасын және ондай нүктелер саны шектеулі болсын;
3) Берілген 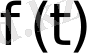функциясының өсу дәрежесі шектеулі болсын, яғни барлық 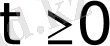мәндерінде 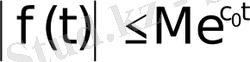теңсіздігі орындалатындай 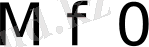және 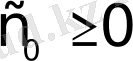сандары табылсын. Осы шартты қанағаттандыратын 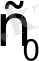сандарының ең кішісі функциясының өсу көрсеткіші деп аталады.
Осы (1)-(3) шарттарды қанағаттандыратын функциясы түпнұсқа деп аталады.
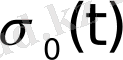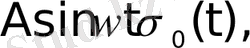
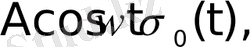
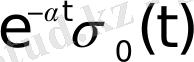
Автоматты жүйелердегі құбылыстарды сипаттағанда кездесетін көптеген функциялар түпнұсқа болады. Мысалы, Хевисайдтың бірлік функциясы деп аталатын функциясы, 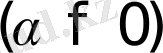функциялары түпнұсқа болады. Бұл функциялардың бірлік баспалдақты функция түріндегі көбейткіштерінің бар болуы түпнұсқаның (1) шартының орындалуын қамтамасыз етеді. Оны физикалық тұрғыдан түсіндірудің ешқандай қиындығы жоқ. Шынында да, автоматты жүйелердегі құбылыстар қандай да бір белгілі уақыт кезеңінен басталады.
Осы уақытты алғашқы уақыт кезеңі ретінде алуға болады. Сонда t 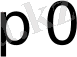болғанда f(t)=0 болады да түпнұсқаның (1) шарты орындалады.
Ал (2) және (3) шарттар автоматты жүйелерді сипаттайтын көптеген f(t) функциялары үшін орындалады.
Егер осы (1)-(3) шарттардың ең болмағанда біреуі орындалмаса, онда f(t) функциясы түпнұсқа болмайды. Мысалы, функциялары түпнұсқа болмайды.Бұл функциялар үшін (3) шарт орындалмайды.
Түпнұсқаның (3) шартын қанағаттандыратын функциялардың мысалын келтірейік:
а) Барлық шектелген функциялар; мұндай функциялар үшін өсу көрсеткіші 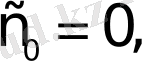өйткені
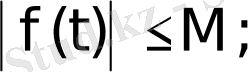
б) Барлық түріндегі дәрежелік функциялар. Бұлар үшін 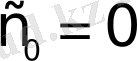болады. Шынында да

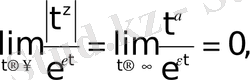
өйткені 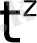-тің модулі көрсеткіштік функциясына қарағанда баяу өседі. Мұндағы 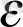-қаншалықты болса да аз оң сан.
Осыдан 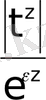функциясының аралығында шектелген функция екендігі көрінеді. Басқаша айтқанда, барлық 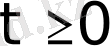мәндері үшін 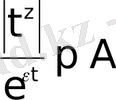, немесе теңсіздігі орындалады.
Мұндағы А-кез-келген оң сан, 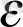-қаншалықты болса да аз оң сан. Сондықтан 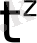функциясының өсу көрсеткіші 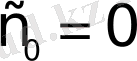болады.
Егер 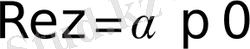болса, онда 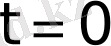үзіліс нүктесі болады да 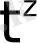функциясы түпнұсқаның (3) шартын қанағаттандырмайды.
Жоғарыдағы

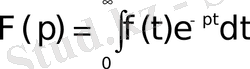
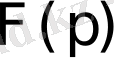теңдігімен анықталған комплекс айнымалының функциясы функциясының Лаплас бойынша бейнесі деп аталады. Осы (1) теңдіктің оң жағындағы интеграл Лаплас интегралы деп аталады. Анықтама бойынша бұл меншіксіз интеграл мынаған тең:

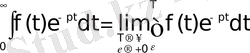
Мұндағы оңжақтық шекке көшу амалын көрсетеді. Лаплас интегралының көмегімен функциясы мен оның 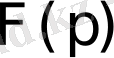бейнесі арасында сәйкестік орнатылады.
Берілген функциясы бойынша оның 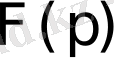бейнесін табу амалы Лаплас түрлендіруі деп аталады. Ол былай белгіленеді:
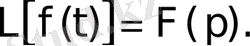
Егер функцияға 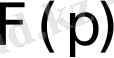бейнесі сәйкес келсе, ол сәйкестік әдетте былай жазылады: 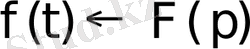немесе .
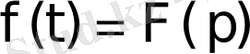Егер (2) теңдіктің оң жағындағы шек бар болатын болса, онда Лаплас интегралы жинақталады.
Енді Лаплас бойынша қандай функцияларын түрлендіруге болатынын қарастырайық.
Теорема 1.1
Егер функциясы түпнұсқа болса, онда оны Лаплас бойынша түрлендіруге болады және оның 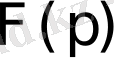бейнесі жарты жазықтығында анықталған.
Мұндағы 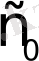деп функциясының өсу көрсеткішін ұғамыз.
Теореманы дәлелдеу үшін р комплекс айнымалысының жазықтығының теңсіздігі орындалатын бөлігінде (1) теңдіктің оң жағындағы интеграл жинақталатындығын көрсетсек жеткілікті.
Түпнұсқаның (3) шартын пайдаланып мынадай теңсіздіктер аламыз:

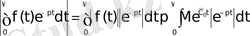
Ал 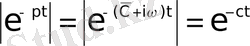болғандықтан

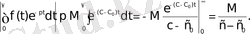
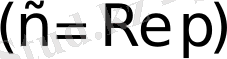Мұндағы болғандықтан, болса, Лаплас интегралы жинақталады. Сонымен, функциясы түпнұсқа болса, онда оны Лаплас бойынша түрлендіруге болады. Оның 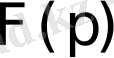бейнесі р комплекс айнымалысы жазықтығының жорымал оске параллель және одан 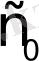қашықтықта өтетін түзуден оңға қарай бөлігінде анықталған.
Осы теоремадан 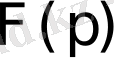бейнесінің мынадай қасиетін алуға болады.
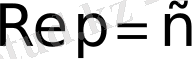Егер (3) теңсіздікте шексіздікке ұмтылса, онда Лаплас интегралының модулі нолге ұмтылады.
Осыдан 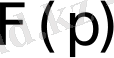функциясы бейне болса, онда

болатындығы шығады.
Теорема 1.2
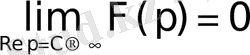
түпнұсқаның 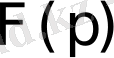бейнесі шарты орындалатын жарты жазықтықта аналитикалық функция болады.
Мұндағы 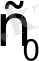-түпнұсқаның өсу көрсеткіші.
Анықтама
Мына
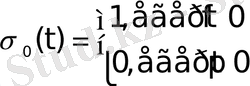болса,

шартымен анықталған 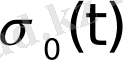функциясы Хевисайдтың бірлік функциясы деп аталады.
Осы 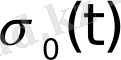функциясы түпнұсқа болады. Оның өсу көрсеткіші 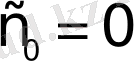. Бұл функцияның мәні 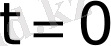болғанда анықталмаған, өйткені Лаплас интегралын есептегенде 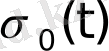функциясының 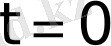болғанда қандай мән қабылдайтыны ескерілмейді.
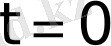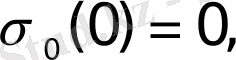
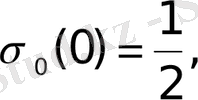
Дегенмен де, нүктесіндегі мәні үшін әдетте 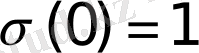мәндерін алады.
Берілген функциясы - аралықта анықталсын және түпнұсқаның (2), (3) шарттарын қанағаттандырсын. Ал болғанда 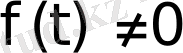шарты орындалсын. Егер 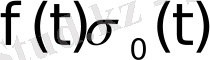функциясын қарастырсақ, яғни
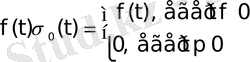болса,
онда 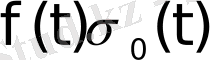функциясы түпнұсқа болады. Мұндағы 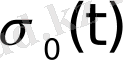көбейткіші түпнұсқаның (1) шартының орындалуын қамтамасыз етеді. Сондықтан, алдағы уақытта функциясының Лаплас түрлендіруінде 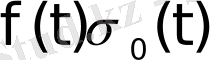функциясы берілген деп есептеп, оның орнына қысқаша деп жазамыз.
Енді кейбір функциялардың бейнесін анықтама бойынша табу мысалдарын келтірейік.
1 мысал
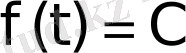функциясының бейнесін табу керек. Мұндағы 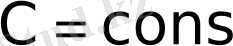(нақты немесе комплекс сан).
Шешуі
Анықтама бойынша

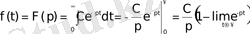
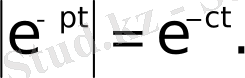Егер деп алсақ, онда Сондықтан, егер 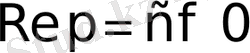болса, онда 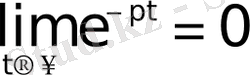болады. Нәтижесінде мынадай сәйкестік аламыз:

0
Re

,

p
р
с
С

Дербес жағдайда

0
Re

,
1
1

p
p

2 мысал
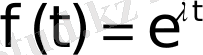функциясының бейнесін табу керек.
Мұндағы (нақты немесе комплекс сан).
Шешуі
Егер 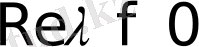болса, онда 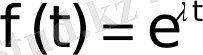функциясының өсу көрсеткіші егер болса, онда функциясы шектелген болады да 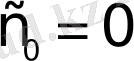мәнін аламыз. Берілген функцияның Лаплас түрлендіруін жазайық:

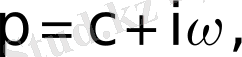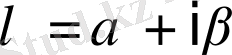Мұндағы ал болсын. Олай болса 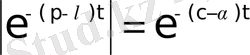теңдігін аламыз. Осыдан, егер 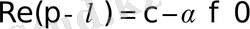болса, онда 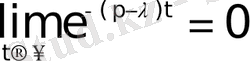мәні шығады.
Нәтижесінде

Re
Re

,
1

p
p
e
t

сәйкестігін аламыз.
Дербес жағдайда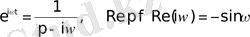

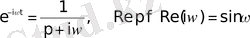
Мұндағы ω-кез-келген комплекс сан.
3 мысал
функциясының бейнесін табу керек.
Шешуі
болғандықтан, функциясының өсу көрсеткіші
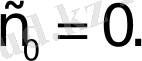
Берілген функцияның Лаплас түрлендіруін табайық

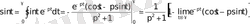
Егер болса, онда

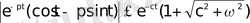
теңсіздігі алынады.
(Мұнда )
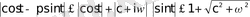Сонда егер 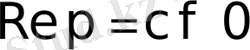болса, онда 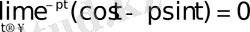аламыз.
Сондықтан

0
Rep

,
1
1
sin
2

p
t

4 мысал
f(t)=cost функциясының бейнесін табу керек.
Шешуі
cost 1 болғандықтан cost функциясының өсу көрсеткіші с=0.
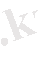
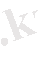
Бұл функцияның Лаплас түрлендіруін жазамыз:

Жақшаның ішіндегі функцияның шегі жоғарыда көрсетілгендей нолге ұмтылады. Сондықтан

0
Re

,
1
cos
2

p
p
p
t

1.3 Меллин формуласы
Берілген 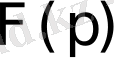бейнесінен оған сәйкес түпнұсқасына көшу үшін Лапластың кері түрлендіруі орындалады.
Теорема 1.3
Түпнұсқа үздіксіздік нүктелерінде

i
c
i
c
pt
dp
e
p
F
i
t
f

)
(
2
1
)
(

теңдігімен анықталады.
Мұндағы 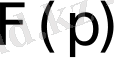функциясы түпнұсқасының Лаплас бойынша бейнесі. (14) теңдіктің оң жағындағы интеграл бас мәні ұғымында анықталады. Басқаша айтқанда

i
c
i
с
i
c
i
c
pt
pt
dp
e
p
F
dp
e
p
F

)
(
lim

)
(
арақатынасы орындалады да, интеграл жарты жазықтығында жатқан және жорымал оське параллель түзу бойынша алынады.
(14) формула Меллиннің кері айналдыру формуласы деп аталады. Ол 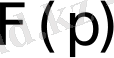бейнесі мен түпнұсқасын байланыстырады.
Берілген 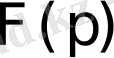бейнесі бойынша түпнұсқаны табу Лапластың кері түрлендіруі болып табылады. Оны былай белгілейді:

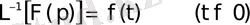
Мұндағ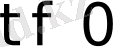ы шарты болғанда функцияның 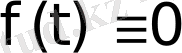шартын қанағаттандыратынын көрсетеді.
(14) формула бейнені тек үздіксіздік нүктелерінде ғана анықтайды. Бірақта түпнұсқаның бірінші текті үзіліс нүктелері болуы мүмкін.
Бұл жағдайда түпнұсқаның үзіліс нүктелерінде

)
0
(
)
0
(
2
1

)
(
2
1
lim

t
f
t
f
dp
e
p
F
i
i
c
i
c
pt

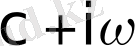
шарты орындалатындығын көрсетуге болады.
Сонымен, айналдыру формуласы 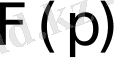бейнесі бойынша түпнұсқасы оның үзіліс нүктелеріндегі мәндеріне дейінгі дәлдікпен анықталады. Түпнұсқаға (1.1) формула бойынша анықталған бір ғана бейне сәйкес келеді. Өйткені түпнұсқаның үзіліс нүктелеріндегі мәндері бейненің түрін өзгертпейді. Дегенмен де бір бейнеге бір-бірінен айырмашылығы үзіліс нүктелеріндегі мәндерінде болатын түпнұсқалар жиынын сәйкес қоюға болады.
Егер түпнұсқасы аралығында дифференциалданатын функция болса, онда берілген бейне бойынша бір ғана түпнұсқа анықталады.

1.2 Лаплас түрлендіруінің қасиеттері

Егер 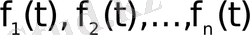функциялары түпнұсқалар, ал олардың бейнелері тиісінш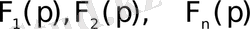е және 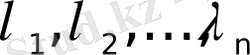шамалары t-мен р-ға тәуелсіз болса, онда мына арақатынастар орындалады:

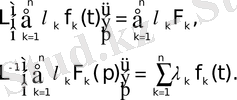
Шынында да, (1.1) формулаға сәйкес

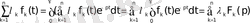
Егер 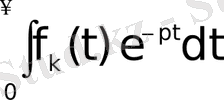интегралы 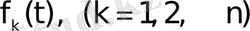функциялары үшін 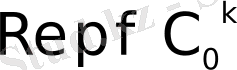жарты жазықтығында жинақталса, онда 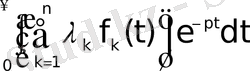интегралы 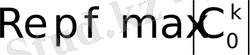жарты жазықтығында жинақталады.
5 мысал
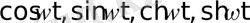функцияларының бейнесін табу керек.
Мұндағы ω-нақты немесе комплекс сан.
Шешуі
Комплекс айнымалының функциясының теориясынан белгілі формулаларды жазайық:

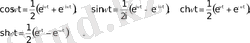
Бейненің сызықтылығын және (9) 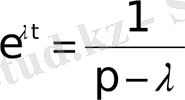формуласын пайдаланып керекті сәйкестіктерді аламыз.

Re
Re

1
1
2
1

Re
Re

1
1
2
1
Im
)
Re(
Re

1
1
2
1
sin
Im
)
Re(
Re

1
1
2
1
cos
2
2
2
2
2
2
2
2

p
p
p
p
t
sh
p
p
p
p
p
t
ch
i
p
p
i
p
i
p
i
t
i
p
p
p
i
p
i
p
t

6 мысал
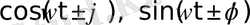функцияларының бейнесін табу керек.
Мұндағы ω, φ-кез-келген нақты немесе комплекс сандар.
Шешуі
Белгілі формулаларды жазайық:

Бейненің сызықтылығын және (18), (19) формулаларды пайдаланып мына сәйкестіктерді аламыз:

Im
Re

sin
cos
)
sin(
Im
Re

sin
cos
)
cos(
2
2
2
2

p
p
p
t
p
p
p
t

Теорема 2.2
Егер өсу көрсеткіші 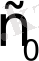болатын функциясы мен оның 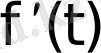туындысы түпнұсқалар, ал 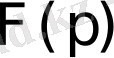функциясы түпнұсқасының бейнесі болса, онда мынадай сәйкестік орындалады:

Re

),
0
(
)
(
)
(
0
с
p
f
p
pF
t
f

Дербес жағдайда, егер 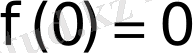болса, онда

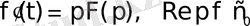
Дәлелдеу үшін 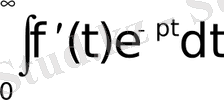интегралын бөліктеп интегралдаймыз:

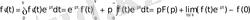
Ал 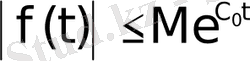болғандықтан

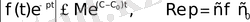
бағалауын аламыз.
Сондықтан 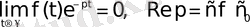болады да 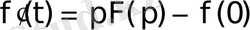сәйкестігін аламыз.
Бұл қасиетті жалпылауға болады.
Егер өсу көрсеткіші 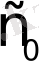болатын 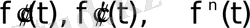туындылары түпнұсқа болса, онда мынадай сәйкестіктер алуға болады:

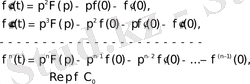
Дербес жағдайда, егер 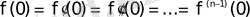болса, онда

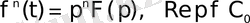
7 мысал
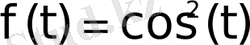функциясының бейнесін табу керек.
Шешуі
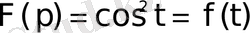болсын дейік. Сонда
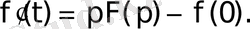
Бірақ 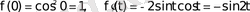болғандықтан

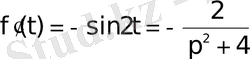
Сонымен
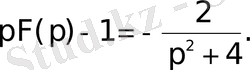
Осыдан 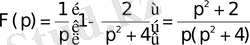аламыз.
Осы нәтижені 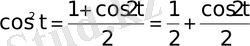теңдігі арқылы да алуға болады.

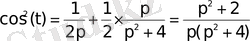
Егер -түпнұсқа, ал 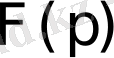оның бейнесі болса, онда

Re

,
)
(
)
(
0
0
с
p
p
p
F
dt
t
f
t

Дәлелдеу үшін 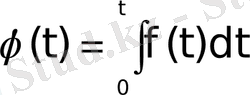деп белгілейік те, түпнұсқаны дифференциалдау теоремасын пайдаланайық. Сонда 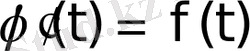алынады.
Егер 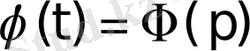сәйкестігін белгілесек 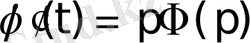деп жазуға болады. Мұнда 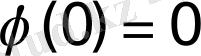екендігі ескерілген. Ал 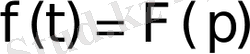болғандықтан 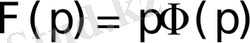сәйкестігі шығады. Осыдан 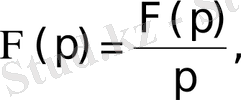яғни

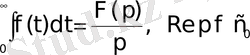
8 мысал
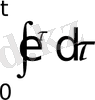функциясының бейнесін табу керек.
Шешуі

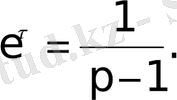
Түпнұсқаны интегралдау формуласы бойынша берілген функцияның бейнесін табамыз.

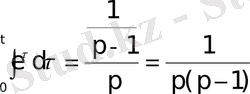
1.3 Шектік есептерді шешудің вариациялық әдістері

Функционал және оператор. Функционалдық анализдің осы тақырыпқа қажетті ұғымдарын атап өткен дұрыс.
1-анықтама. К={g(x)}, мұндағы x - тәуелсіз айнымалы немесе бірнеше тәуелсіз айнымалылар жиыны х=(х1,х2, ...,хn) әлдебір функция класы немесе жиыны берілсін. I=I[g(x)] айнымалы шамасы g(x) функциясынан функционал (функциядан функция) деп айтады, егер әрбір g(x)K функциясы үшін берілген ереже немесе заң бойынша I анықталған сан сәйкес қойылса.
Берілген функционал анықталған К={g(x)} функциялар класы функционалдың анықталу облысы немесе функционалдың берілу облысы деп аталады, ал функциялардың өздері мүмкін функциялар деп аталады.
1-мысал.
К={g(x)} функциялар класы - х=0 нүктесінде дифференциалданатын функциялар жиыны болсын. k=g(0) санын К облысында анықталған g(х) функциясының функционалы деп қарастыруға болады.
2-мысал.
[a, b] аралығында үзіліссіз дифференциалданатын, яғни g(x)C(1)[a, b] болатын g(х) функциясының К жиынын қарастырайық. x=a және x=b нүктелері арасындағы g=g(x) қисығының s доғасының ұзындығы K облысында g(x) функциясынан 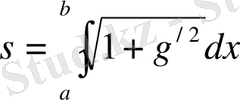формуласымен өрнектелетін функционалы болады.
3-мысал.
К - G облысында тұйықталған үзіліссіз және Г шекарасында нөлге айналатын барлық теріс емес z=f (x,y) функциялар жиыны болсын. 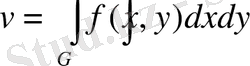көлемі f(x,y)-тен функционал болады.
2-анықтама. К функциялар жиыны сызықты деп аталады, егер әрбір uK және vK функциялары үшін u+vK қосындысы да осы жиында жатса, сонымен қатар uK (- кез келген тұрақты) болса.
Полиномдар жиыны, барлық үзіліссіз функциялар жиыны, облыстың шекарасында нөлге айналатын функциялар жиыны сызықты функциялар жиыны бола алады.
3-анықтама. I=I[g] функционалы сызықты деп аталады, егер ол К сызықты функциялар облысында анықталған болса және кез келген мүмкін u, v функциялар жұбы үшін келесі қатынас ақиқат болса:
I[u+ u]= I[u]+ I[v]
мұндағы және кез келген тұрақты.
k=g[] (0) функционалы сызықты бола алады.
4-анықтама. К={g(x)} жиынында L операторы анықталған дейді, егер әрбір g(x)K функциясы үшін әлдебір заң бойынша жалғыз ғана z=z(x) функциясы сәйкес қойылса. (Сонымен қатар, z(x) функциясы басқа t=(t1, ... , tm айнымалыдан тәуелді болуы мүмкін).
Бұл функциялар арасындағы сәйкестік келесі түрде белгіленеді:
Z=Lg z=L(g)
берілген L операторы анықталған g=g(х) функциясының К жиыны бұл оператордың берілу облысы деп аталады, ал функциялар gК мүмкін функциялар деп аталады.
5-анықтама. L операторы сызықты деп аталады, егер ол сызықты жиында анықталған болса және кез келген мүмкін u және v функциялар жұбы үшін сызықты комбинациялары u +v ( және - еркін тұрақты) да мүмкін функциялар болып, сонымен қатар
1) L(u) = Lu;
2) L(u+v) = Lu+ Lv, шарттары орындалса.
Бұдан кез келген және үшін L(u + v) = Lu +Lv екендігі шығады.
К - облысында анықталған, нақты, үзіліссіз {u} функциялар жиыны болсын. Егер uK және vK болса, онда (u,v)= 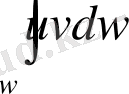саны u және v функцияларының скаляр көбейтіндісі деп аталады және (u,v)=(v,u) болатыны сөзсіз.
6-анықтама. облысында үзіліссіз берілген u сызықты функциялар жиынында L сызықты операторы анықталған болсын. Оның Lu мәндері де облысында анықталған және үзіліссіз функциялар болады. Онда L сызықты операторы симметриялы деп аталады, егер кез келген мүмкін u және v функциялар үшін келесі қатынастар ақиқат болса:

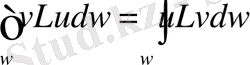
яғни
(Lu,v)=(u,Lv) (1)
Егер кез келген мүмкін u функциясы үшін u0 болғанда ғана (Lu, u)0 теңсіздігі орындалса, онда L оператоы оң оператор деп аталады.
4-мысал.
gС(2)[0,1] функциялар жиынында анықталған Lg=-gn операторын қарастырайық және g(0)=0, g(1)=0 болсын.
Егер u және v мүмкін функциялар болса, онда 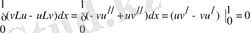болады, сондықтан
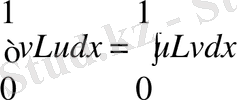, яғни (Lu,v)=(u,Lv) болады және L7 операторы симметриялы деп есептеледі. Сонымен қатар u0 екенін ескерсек, шекаралық шарттардың күші бойынша u!=0 болғанда
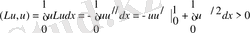болатын u0 жалғыз мүмкін функция табылады және u≡0 болса, онда (Lu,u)=0 болады. Яғни L операторы оң оператор болады.
Вариациялық есеп

I=I[g(x)] (2)
функцияоналы К={g(x)} жиынында анықталған функционал болсын.
(2) функционалының экстремумдарын іздеу есебі вариациялық есеп деп аталады. Одан гөрі дәлірек айтсақ (1-сурет): g=g(х) барлық мүмкін функциялар үшін минимум жағдайында I[g]I[g] теңсіздігі орындалатын немесе максимум жағдайында I[g]I[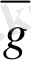] теңсіздігі орындалатын функцияға жеткілікті жуық 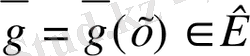функциясын табу керек. g және функцияларының ара қашықтығын әртүрлі түсінуге болады.
у
х
x
0
g=g(х)
А
В
а
b

1-сурет - (2)-есептің геометриялық мағынасы.

1-мысал: М(а,А) және N(b,B) нүктелерінен өтетін g=g(х) жатық қисықтары арасынан доғасының ұзындығы ең кіші түзуді табу керек болсын.
Есеп С(1)[a,b] класына жататын g=g(х) қисықтары үшін және g(а)=А, g(b)=B болатын келесі функционалдың минимумын табуға келеді:

Геометриялық мағынасына көңіл аударсақ: ізделінді түзу
болады.

Негізгі теоремалар
Г шекаралы G облысында үзіліссіз коэффициентті (қарапайым немесе дербес туындылы) сызықты дифференциалдық теңдеу берілсін және осы теңдеудің Г шекарасында берілген шекаралық біртекті шарттарды қанағаттандыратын g шешімін табу керек болсын. Бұл теңдеудің сол жағын G+Г облысында жеткілікті үзіліссіз туындылары бар және Г шекарасында шекаралық шарттарды қанағаттандыратын К функциялар жиынында анықталған L сызықты оператор ретінде қарастыруға болады. Сонда есеп келесі операторлық теңдеуді шешуге келеді:
Lg=f(P) (3)
R[g]=0 (4)

Мұндағы Р тәуелсіз айнымалылар тобы, f(P) функциясы - gK болатын үзіліссіз берілген функция, сонымен қатар g функциясы Г шекарасында шекаралық шартты қанағаттандырсын. R - белгісіз сызықты, төмен ретті оператор.
Lg=f(P) (5)
R[g]=(P), РГ (6)
(мұндағы (P) - белгілі функция) біртекті емес шектік есеп
R[g1]= (P) (7)
біртекті шектік есепке келтіріледі, егер g=z+g1 болып, мұндағы z-жаңа белгісіз және g1 - (6)-шартты қанағаттандыратын жеткілікті жатық функция болса. (5) және (6) формулалардан Lz=f(P) - Lg1 және R[z]=0 екенін аламыз. g1 функциясын таңдау арқылы табуға болады. Сонда бұл әдістің идеясы - (2)-(3) - шектік есепті әлдебір функционалға минимум немесе экстремум беретін теңсалмақты есеппен алмастыруға келтіру. Практикада өзімізге таныс белгілеулермен жұмыс жасау үшін g функциясын y деп белгілеуге болады.
Т е о р е м а 1. L операторы - К класында анықталған және оң симметриялы сызықты оператор болсын. Онда (2)-операторлық теңдеу (7.40)-шекаралық шартпен бірге К класында екі шешім қабылдай алмайды, яғни егер шектік есептің шешімі бар болса, ол міндетті түрде жалғыз болады.
Екінші ретті қарапайым дифференциалдық теңдеу үшін құрылған сызықты шектік есепті вариациялық есепке келтіру
(8)
(9)
есебі берілсін. Бұл есептің шешімін келесі түрде іздейміз:
(10)
Мұндағы z(x) функциясы - шекаралық шарттары біртекті болатын біртекті емес теңдеудің шешімі:
(11)

Ал z1(x) функциясы - шекаралық шарттары біртекті емес болатын біртекті теңдеудің шешімі:
(12)

Ал z2(x) функциясы - шекаралық шарттары біртекті емес болатын біртекті теңдеудің шешімі болады:
(13)

(11)-(13)- есептерді шешіп, (10)-формула мен (9)-шекаралық шарттарды қолданып с1 және с2 коэффициенттерін анықтайтын жүйені құруға болады.
(14)
(14)-жүйені шығару арқылы у(х) белгісізін тауып, оны (8)-(9)-есепке қою арқылы шектік есепті шешеміз.
Мысалы:
(15)
Шешуі:
1. Біртекті шекаралық шартты біртексіз теңдеу құрамыз:
(16)

2.Біртексіз шекаралық шартты біртекті теңдеу құрамыз:
(17)
3.Біртексіз шекаралық шартты біртекті теңдеу құрамыз:
(18)
4. (16)-(18)-есептерді 1-ретті дифференциалдық теңдеулер жүйесі үшін Коши есебіне келтіреміз:
T(x)=z(x), белгілеулерін енгізейік. Сонда
(19)
T1(x)=z1(x), белгілеулерін енгізейік. Сонда
(20)
T2(x)=z2(x), белгілеулерін енгізейік. Сонда
(21)
есептері құрылады. Бұл есептердегі Т(х), T1(x), T2(x) функциялары (16)-(18)-есептердің шешіимдері болады, ал функциялары осы шешімдердің туындылары болады.
5. Т(х), T1(x), T2(x) функциялары табылған соң (14)-формула бойынша с коэффициенттерін табуға арналған жүйе құрамыз:

екенін ескерсек, болады.
екенін ескеріп, (14)-ке қойсақ: сонда болады. Келесі теңдеуіне қойсақ:

6. с2-ні табу үшін алдымен (19)-(21)-есептерді Эйлер әдісімен шешіп Т(хk), T1(xk ), T2(xk ), мәндер кестесін құру керек. Сосын с2-ні тауып формуласына қою арқылы у(хk) шешімдерін тауып алуға болады.
Галеркин әдісі
Вариациялық, ақырлы-айырымдық әдістерді қолдану барысында шектік есептің шешімі кесте лық мәндер түрінде алынады. Ал Галеркин әдісі аналитикалық әдіске жатады.
y +p(x) y + q(x) y = f(x) (22)
(23)
мұндағы p(x), q(x), f(x) - функциялары [a,b] аралығында үзіліссіз функциялар, ал 0,1,0,1, A,B - берілген тұрақтылар және 0+10, 010 шектік есебі берілсін.
Белгілеу енгізейік:
L[y]=y +p(x) y + q(x) y (24)
(25)
[a,b] аралығында базистік функциялар жүйесі берілсін
(26)
және олар келесі шарттарды қанағаттандырсын:
1 (26)-жүйе ортогональды болсын, яғни
(27)
2 (26)-жүйе толық жүйе болсын, яғни барлық функцияларына ортогональ нөлден өзгеше басқа бір де бір функция жоқ болсын.
3 ақырлы базистік функциялар жүйесі төмендегі біртексіз (28)-шарттарды қанағаттандыратындай болып, ал функциялары төмендегі біртекті (29)-шарттарды қанағаттандыратындай болып таңдалынып алынуы керек:
(28)
(29)
(22)-(23)-шектік есептің шешімін
(30)
түрінде іздейміз. (28), (29)-шарттардан бұл функцияның (23)-шартты қанағаттандыратыны көрінеді.
Байныспаушылық (невязка) өрнегін қарастырамыз:
(31)
сi коэффициенттерін байналыспаушылықтың квадратының интегралының мәні
(32)
өте аз шама болатындай етіп таңдап алу керек. Бұл тек қана байланыспаушылық базистік функциялардың барлығына ортогональды болса ғана орындалатыны дәлелденген ([2], [13], [18] қараңыз).
Ортогональдылық шарты:

немесе
(33)
(33)-ден сызықты алгебралық теңдеулер жүйесін аламыз, оны сi-ға қатысты шешу керек болады. Мұндай жүйені шешудің сандық әдістерін жоғарыда келтіргенбіз.
Мысалы:
Галеркин әдісін қолданып
(34)
у(0)=у(1)=0 (35)
шектік есептің шешімін табу.
Ui базистік функциялар жүйесін таңдап аламыз:

Бұл функциялар сызықты тәуелсіз және нөлдік шекаралық шарттарды қанағаттандырады. Жуық шешімін мына түрде іздейміз:
(36)
Бұл теңдеуді (34)-теңдеудің сол жағына қою арқылы байланыспаушылықты аламыз:
. (37)
R функциясының u1(x) және u2(x) функцияларына ортогональдылығын ескерсек:

Бұл жүйеге (7.77) - шешімді қойсақ және интегралды есептесек, келесі сызықты алгебралық теңдеулер жүйесін аламыз:

Бұл жүйені шешсек . Бұл мәндерді (37)-ға қойсақ:
.
Бұл есептің дәл шешімі . Берілген аралықты 0,25 қадаммен бірнеше бөлікке бөліп әр нүктедегі функция мәндерін алып салыстырсақ, төмендегі 22-кестеден қателігінің қаншалықты екенін анықтауға болады.

1-кесте - (34-35)-есептің мәндер кестесi.
xi
0.25
0.50
0.75
yi
0.044
0.069
0.060
Y
0.044
0.070
0.050

Егер (22)-теңдеудің коэффициенттерін есептеу қиынға соғатын болса бұл әдістен гөрі ақырлы-айырымдық немесе қуалау әдістерінің бірін қолдануға болады.
Қуалау және ақырлы-айырымдық, вариациялық әдістерді қолданып төмендегі қарапайым дифференциалдық теңдеулер үшін шектік есептер:
a) , y(0)=1; y(1)=e-1+1=1.367; e=10-2
b) , y(0)=1; y(1)=e-1+1=1.367; e=10-2
c) , y(0)=1; y(1)=e-1+1=1.367; e=10-2
d) , y(0)= y(1)=0, a=1+0,4k,
k=0,1,2.,
b=2,5+0,5n, n=0,1,2,3,4,5.
e) , y(0)=y(1)=0, a=1+0,4k, k=0,1,2.,
b=2,5+0,5n, n=0,1,2,3,4,5.
f) , y(0)= y(1)=0, a=1+0,4k, k=0,1,2.,
b=2,5+0,5n, n=0,1,2,3,4,5.

2. ФУНКЦИОНАЛДЫ ТАЛДАУДАҒЫ СЫЗЫҚТЫ ОПЕРАТОРЛАР ТЕОРИЯСЫ

2.1 Lp кеңістігі және сызықтық оператор

1-анықтама. f(x) өлшемді функциясы жоғарғыдай біз функциялардың шектелуін кейбір берілген [a, b] сегментінде р-дәрежелі қосындыланатын деп аталады. Мұндағы p1, егер
.
Мұндай функциялар жиыны Lp арқылы белгілеу қабылданған (немесе Lp[a,b] арқылы). L1=L екені айқын.
1-теорема. f(x) функциясы, р1 дәрежелі қосындыланатын яғни Lp L қосындыланады.
Расында да егер E=[a, b], A=E(), B=E-A болса, онда f(x)-функциясының қосындыланатын А-жиынында айқын, ал оның В-жиынында қосындылатыны мына жиынынан шығады. 2 - теорема осы сияқты дәлелденеді.
2-теорема. Lp-ға кіретін екі функцияның қосындысы да осы класқа кіреді.
Шынында да, f(x) және g(x) Lp-ға кіреді делік.
E=[a, b], A=E, B=E-A десек, онда үшін шығатыны:
,
бұдан

екендігі шығады.
Осылайша біз шекті интегралданатынына көз жеткіземіз. f(x) функиясымен бірге кез келген k f(x) - функциясы да Lp-ға кіреді.
Мұндағы k - шекті тұрақтылық.
р1 болсын. саны р-ға түйіндес көрсеткіш деп аталады.

болаиыны себепті q-ға түйіндес көрсеткіш р бар, демек бұл р және q өзара түйіндес көрсеткіштер. Дербес жағдайда, егер р=2, онда q=2, яғни 2 өзіне түйіндес.
3-теорема. Егер , ал , мұндағы р және q өзара түйіндес, онда f(x)g(x) көбейтіндісі қосындыланады және
(1)
теңсіздігі дұрыс.

Дәлелдеуі: 0α1 болсын.
(0x+)
функциясын қарастырайық.
Оның туындысы болғанда оң, ал x1 болғанда теріс. Олай болса x=1-де функциясының ең үлкен мәнге жетеді. Осылайша , бұдан шығатыны барлық x0 мәнінде
(2)
шығады.
А және В екі оң сан болсын. Егер (2)-ге x=AB орнына қойып және алынған теңсіздікті В-ға көбейткеннен шығатыны
.
Теореманың шарттында айтылғандай, p және q - екі өзара түйіндес көрсеткіштер болсын. Егер болса, онда бізде
(3)
шығады.
Бұл теңсіздіктер A0 және B0 үшін дәлелденген. Осы сандардың біреуі (немесе екеуі) 0-ге айналса, ол теңсіздік әр уақытта дұрыс орындалады.
Осыдан кейін теоремада айтылғандай f(x) және g(x) функцияларын қарастырамыз.
Егер бұлардың ішінен тек біреуі нөлге эквивалентті болса, онда теореманың барлық тұжырымдары орынды. Бұл ерекше жағдайды есептемей, екі интегралды

қатал оң деп тұжырымдап, мына функцияларды аламыз:
, .
Егер (3) - ке апарып қойсақ, одан шығатыны
, (4)
бұдан f(x)γ(x) көбейтіндінің қосындылануы, ал мұнымен бірге f(x)g(x) көбейтіндісі шығады.
Сонымен қатар

екенін ескеріп және (4) - ті интегралдап,
,
табамыз, бұдан (1) - ден күштірек
,
L(1) теңсіздігі Гëлдер теңсіздігі делініп, p=2 болғанда Буняковский теңсіздігінің жалпылауы деп аталынады.
4-теорема. Егер және (), онда
(5)
Дәлелдеуі: Теоремада p=1 екені айқын. p1 және q p-ға түйіндес көрсеткіш болсын.
Теоремадағы f (x)+g(x) екі қосынды Lp - да жатады, себебі Lp - да жатады.
(6)
береді. Осы сияқты
. (7)
Бірақ . Демек
.
(6) және (7) - ден шығатыны
,
ал бұдан келіп теорема шығады. [ - ға қысқартылуы заңды, егер бұл теорема нөлден өзгеше болса, бірақ кері жағдайда теорема айқын].
(5) - і теңсіздігі Минковский теңсіздігі деп аталады. p=2 болғанда бұл бізге белгілі. Коши теңсіздігіне айналады.
Бұл пайымдаумен Гëлдер мен Минковскийдің теңсіздігі анықталады:
, (8)
. (9)
2-анықтама. болсын.

саны f(x) функциясының нормасы (Lp - ның элементі сияқты) деп аталады.
Норманың келесі қасиеттері айқын:
І. және сонда тек қана сонда
ІІ. және дербес жағдайда
ІІІ. .
Норманың кіріспесі Lp және L2 үшін де геометриялық терминологияны орындауға болатынын көрсетеді.
Элементтердің жүйелі жинақтылығы - ден шегіне норма бойынша
.
Жинақтылықтың бұл түрін орташа ретті жинақтылық деп атайды. Осылайша L2 үшін де жинақтылықтың кейбір жүйесінен р орташа ретті өлшем бойынша жинақтылық шығады. Осылайша L2 үшін шектің жалғыздығы және норманың өзара эквивалентті функциялығы шығады. Сонымен қатар L2 сияқты Lр элементтінің жүйелілігімен өзіне жинақталу түсінігі енгізіледі және дәлелденеді (Lр кеңістігінің толықтығы).
Бұл жерде біз жаңа идеялық моменттің болмағаны себепті сөйлемнің дәлелдеуіне тоқталмаймыз. Тура осылайша біз дәлелдеусіз §2 - гі 6-теоремадағы (соңғы b-a=2PI) M, C, P, S және T кластарының әрбіреуі Lр - ға барлық жерде тығыз.
Жинақтылықтың әлсіз түсінігі p1 болғанда былай болады: жүйелілігі - ға әлсіз жинақталады, егер теңсіздік
(10)
Lp- дағы g(x) - функциясының кез келген орнын алатын болса, мұндағы q p - ға түйіндес көрсеткіш.
Гëлдер теңсіздігін пайдалана отырып орташа жинақталу жүйелілігінің (сол шекке) әлсіз жинақталатынын көрсете аламыз.
Егер p=1 болса, түйіндес көрсеткіш болмайды. Мұндай жағдайда жүйелілігі, егер (10) теңсіздігі функцияның орнын алатын болса, - ге әлсіз жинақталады.
Қорытындылай келе талдауда кеңістігінде қолданылатын (мұндағы ) тағы бір типтегі кеңістікті келтірейік.
нақты санының Lp кеңістігінде жиынның барлық жүйелілігін x=(x1, x2, x3, ...) түсінеді.

саны элементінің нормасы деп аталынады. Жоғарыда айтылғандай үшін Lp элементі енгізіледі. kx - көбейтіндісі k сан, ал элементі.
Норма енді әдеттегі қасиетке ие.
І. және сонда тек қана сонда x=0.
ІІ. және дербес жағдайда .
ІІІ. .
Алғашқы екі қасиет айқын, ал үшінші (9) - дан шығады. Норманың түсінігін пайдалана отырып өзіне жинақталу жиынында, барлық жерде тығыз элементінің жүйелілігінің шектік түсінігі келіп шығады. элементінің жүйелілік шегі жалғыз ба, норма үзіліссіз бе, - кеңістігі толықтық қасиетіне ие бола ма бұған біз тоқталмаймыз.
Е және Е1 - екі сызықтық топологиялық кеңістік болсын.
Сызықтық операторда Е Е1 деп
y= Ax,
шартты қанағаттандыратын
айтады.
DA жиынтығы А - бейнелеуі үшін анықталып, А операторының анықталу облысы деп айтады. Жалпы айтқанда DA=Е деп ұйғарылмайтын, бірақ біз оны әрқашан да DA сызықтық көпбейне деп есептеп, яғни егер , онда барлық үшін .
А операторы нүктесінде үзіліссіз болады, егер нүктесінің кез келген V маңайында х0 - нүктесінде U маңайы бар болып, АхN болса, онда хUDA . А операторы үзіліссіз DA жиынында егер ол әрбір нүктеде үзіліссіз болса.
Е және Е1 нормалданған кеңістік болғанда мына анықтама келесіге пара - пар. А операторы үзіліссіз деп аталады, егер кез келген үшін бар болса, мына теңсіздіктен

бұдан шығатыны

жиыны Ах=0 үшін А сызықтық операторының ядросы деп аталады, KerA деп белгіленеді. жиыны А сызықтық оператордың бейнесі деп аталып, ImA деп белгіленеді. Ядро сияқты, сызықтық оператордың бейнесі де сызықтық көпбейнелік болып саналады. Егер оператор үзіліссіз және DA=E онда KerA ішкі кеңістік, яғни тұйық. Сызықтық үзіліссіз оператордың бейнесі Е1-дің ішкі кеңістігі болу міндетті емес, тіпті егер DA=E.
Бұл тараудың басында келтірілген сызықтық функционал ұғымы ол сызықтық операторының дербес жағдайы. Тіптен сызықтық функционал - бұл сандық түзуін берілген Е кеңістігіне аударатын сызықтық оператор. Оператордың сызықтық және үзіліссіздік анықтамасы жоғарыда келтірілген функционалдар анықтамасына сәйкесінше Е1=R болады.

2.2 Сызықтық емес Урысон интегралдық операторының кейбір қасиеттері

G және F - ақырғы өлшемді кеңістікте екі өлшемді жиын болсын. R(t,s,u) функциясы tG, sF , -infinityu+infinity анықталған болсын. Сызықтық емес интегралдық операторын
(1)
Урысон операторы дейді.
1-теорема. R(t,s,u) және R1(t,s,u) функциясы Каратеодори шарттын қанағаттандырады,және
(tG, s F, -infinityu+infinity)
болсын. В1 операторы мен R1(t,s,u) ядросы Lp(F) (0=pinfinity) Lq(G) (0=qinfinity) және үзіліссіз. Онда интегралдық оператор В Lp(F) кеңістігінен Lq(G) кеңістігіне үзіліссіз.
Қарапайым түрде В1 операторы алынып, қасиеті белгілі болған. Осы байланыста Урысон оператор класын ажырату мағынасы болады, оның негізгі қасиеті толық сырттай сызылған. Қазіргі жұмыста Урысон операторының бір класы қарастырылады.
, (2)
мұндағы K(t,s) - нақты өлшенетін функция (tG, -infinityu+infinity). 1-теоремада берілген Lp(F) (1=pinfinity) - дан Lq(G) (1=qinfinity) K операторға үзіліссіз критерий. Салдар сияқты [2] жұмыстың қорытындысынан шығады. K(t,u)=0 және q - бүтін сан. Барлық Lp=Lp(F) (1=pinfinity) - дан ұйғарайық, Lq=Lq(G) (1=qinfinity), ал mesF infinity (mesF - Лебег өлшемінің F жиыны) жағдайда жалпы шенелмеген mesF=1 қоямыз.
1-теорема. К операторы Lp Lq, үзіліссіз болуы үшін келесі шартардың орындалуы қажетті және жеткілікті .
а)
мұндағы =I, егер mesF=I және =0, егер mesF=infinity ал М- оң тұрақты, с (-infinity, +infinity) жатпайды.
б)
Кез келген с1 (-infinity, +infinity) үшін
Дәлелдеуі. Қажеттілігі. Lp - дан Lq - ға К үзіліссіз болсын. Онда жартылай аддитивтік қасиетінен Урысон операторы шығады, К шенелген. Сондықтан [3] теореманың негізінен а) шарты орындалады. Функция

мұндағы және mesF=I Lp - ға бағынады, (Ku)(t)=K(t,c), осыдан және К үзіліссізден б) шарты шығады.
Жеткіліктілігі. а) және б) шарты орындалсын. а) - дан шығады K операторы Lp Lq . Үзіліссіздігін дәлелдейік. Теореманың тұжырымы дұрыс емес ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.