Регрессия моделінің кестесі

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 34 бет
Таңдаулыға:

Мазмұны
Кіріспе 9
Ⅰ БӨЛІМ. 11
Регрессиялық талдау 11
1.1.Регрессиялық талдау (статистикалық тәуелділік және жалпы регрессиялық модельдер). 11
1.2.Статистикалық тәуелділік 12
1.3.Ең кіші квадраттар әдісі 15
1.4Детерминация коэффициенті 20
Ⅱ Бөлім 23
Регрессиялық модель құру 23
2.1.Құмдық коэффинцентін есептеу 23
2.2.Корреляция коэффицентін бағалау 25
Ⅲ.Бөлім 28
Мұнай бағасының өзгерісн зерттеу 28
3.1.Мұнай бағасының өзгеруіне әсер ететін факторлар 28
3.2. Мұнай бағасын болжау әдісі 30
3.3. Регрессиялық модельді құру 37
Қорытынды 40
ҚОСЫМША 45
Қосымша 1.1 Мұнай бағасының коррелограммы 45
Қосымша 1.2 Көмір бағасының коррелограммы 46
Қосымша 1.3 Газ бағасынынң коррелограммасы 47
Қосымша 1.4 Алтын бағасының коррелограммы 48
Қосымша 2. Регрессия моделінің кестесі 49
Қосымша 3. Артық айнымалыларды тексеру тесті 49
Қосымша 4. Регрессия моделінің коррелограммы 50

Кіріспе
Мұнай және табиғи газ энергияның негізгі көздеріне жатады, олардың лидерлік рөлі өткен ғасырдың соңына дейін ғана емес, осы ғасырдың басында да сақталып отыр. Энергияның балама түрлерін пайданудың өсу қарқындарын сөзсіз ұлғайту кезінде мұнай мен газ 2016 жылы, тіпті 2020-2030 жылдары әлемдегі энергияның бүкіл тұтынысының кем дегенде жартысын қамтамасыз ететін болады. Бүкіл XX- ғасыр бойына мұнай ағымдарына үстемдік ету құқығы үшін қатаң күрес болды. XXI ғасырда мұнай бұрынғысынша әлемдегі өте ірі және кең тараған бизнес, саяси ықпалдың өте күшті тетігі болып отыр.
Ұзақ уақыттан бері мұнай ең маңызды энергия көзі болып табылады. Әлемдегі барлық елдер мұнайды тікелей немесе жанама пайдаланады. Қазіргі таңда мұнай өндірумен айналысатын 100-ден астам мемлекет бар. Соңғы мәліметтер бойынша Қазақстан мұнай қоры жөнінен әлемде 16 орын алады екен. Қазіргі мұнайдың бағасы тек өндірушілерді ғана емес, сонымен қатар тұтынушыларды да алаңдатып отыр . Себебі, мұнай бағасының өзгерісі барлық өндіріске әсер ететіні белгілі. Экономикасы тікелей мұнай қораны байланысты мемлекеттер бар . Солардың қатарына Қазақстан да кіреді. Өйткені, Қазақстанның экспорттан ең көп пайда әкелетін өнімі осы мұнай. Сол себепті мұнай бағасын болжау өте маңызды деп ойлаймын.
Қазақстанның мұнай-газ саласының қазіргі кездегі жағдайы жоғары әлеуетімен сипатталады: мұнай мен газдың үлкен запасы, көмірсутектердің игерілген кеніштерінің болуы, мұнайдың өндірісі мен экспортының өсуі. Қазақстанда мемлекеттік бюджетті қалыптастыруда елеулі рөл атқаратын динамикалық дамушы мұнай-газ өнеркәсібі бар. Қазіргі таңда мұнай-газ өнеркәсібінің өнімі жиынтық өнімнің жалпы көлемінің 30 пайыздық үлесін алады. Қазақстан өзін ресурстармен қамтамасыз етіп қана қоймайды, сонымен бірге көмірсутектік шикізаттың ірі экспорттаушысы болып табылады.
Қазақстан Республикасы Президентінің 2030 жылға дейінгі стратегиялық бағдарламасында Қазақстанның мұнай секторына назар аударылады және елдің экономикалық гүлденуі және де ұлттық мұнай ресурстарын тиімді пайдалану арасында параллель жүргізіледі.
Мұнай бағасы көптеген экономикалық процесстерге қатты әсер етеді. Мысалы, мұнай компанияларының акцияларының бағасы, мұнай импорттаушы елдердегі инфляция көрсеткіші, мемлекет экономикасының қарқынды дамуына. Мұнай бағасының өзгерісі альтернативті энергия көздерінің бағасының өзгерісіне тікелей әсер ететінін айта кеткен жөн.
Бұл дипломдық жұмыстың мақсаты мұнай бағасының өзгерісіне әсер ететін факторларды анықтау.
Қойлған мақсатымзға жету үшін бірқатар тапсырмалар орындауымыз қажет:
Мұнай бағасынаң өзгеруіне әсер ететін факторлрды зерртеу;
Мәліметтерді болжауға мүмкіндік беретін тәсілдерді қарасытыру;
Деректерді жинау және талдау;
Регрессиялық модель құру және бағаға әсер етуші факторларды табу;
Мұнай бағасының динамикасын зерртеу әлемдегі маңызды проблемалардың бірі. Және бұл проблеманы шешуге әлемнің көптеген ғалымдары бас қатыруда. Әртүрлі ғалымдар баға динамикасын зерттеу үшін әртүрлі амалдарды пайдаланады, бірақ осы көптеген амал тәсілдердің бірде-біреуін толығымен дұрыс деп айтуға болмайды. Әр амалдың өзінің артықшылықтары мен кемшіліктері бар. Соған байланысты бұл бағытта әлі көптеген зерттеулер жүргізілуі қажет деп ойлаймын.
Соған байланысты бұл жұмыстың негізгі объектісі мұнай бағасы, ал нысаны мұнай бағасының өзгерісі болып табылады.

Ⅰ БӨЛІМ.
Регрессиялық талдау
Кез келген экономикалық көрсеткішке бір ғана емес, көбінесе бірнеше факторлар әсер етеді. Мысалы, кейбір тауарға сұраныс тауар бағасымен ғана емес, басқа оны алмастыратын және толықтыратын тауарлармен, тұтынушы табысымен және көптеген басқа факторлармен анықталады. Бұл жағдайда екі айнымалының сызықтық регрессиясының заңды жалғасы - регрессия моделі қарастырылады. Яғни, регрессиялық талдау (статистикалық тәуелділік және жалпы регрессиялық модельдер) және моделде кездейсоқ фактор болу себептерін, қос сызықтық регрессия және регрессия теңдеуінің сапасын тексерудегі Гаусс-Марков шарттарын және детерминация коэффициентін, сызықтық регрессиялық талдау есебін және ең кіші квадраттар әдісін түсіну.
1.1.Регрессиялық талдау (статистикалық тәуелділік және жалпы регрессиялық модельдер).
Экономика жеке ғылым болып қалыптасқаннан бері зерттеушілер экономикалық дамудың болжамдарын көрсету арқылы экономикалық жағдайларға ықпал етуге тырысты. Бір түрлі экономикалық жағдай дәл солай екінші рет қайталанбайды деп айтуға болады, себебі бір шартта екі стратегияны қолдану мүмкін емес. Сондықтан экономикалық талдаудың негізгі міндеттерінің бірі экономикалық объектінің дамуын болжау.
Кез келген экономикалық көрсеткіш көптеген факторларға тәуелді. Экономикалық модель құруда олардың бәрін қамту мүмкін емес. Әдетте зерттелініп отырған экономикалық көрсеткішке нақты әсер ететін шектелген факторлар алынады, ал ескерілмеген факторлар экономикалық көрсеткіштерге ауытқулар енгізбейді. Нақты ғылымдарда көбіне функционалдық тәуелділік қарастырылады, яғни тәуелсіз айнымалының бір мәніне тәуелді айнымалының бір мәні сәйкес болады. Экономикалық айнымалылар арасында ондай тәуелділік жоқ.
Мысалы: кіріс пен тұтыну арасында, баға мен сұраныс арасында, еңбек өнімділігі және жұмыс стажы арасында қатал тәуелділік жоқ.h4

1.2.Статистикалық тәуелділік
Анықтама 1
Егер кездейсоқ шамасының әрбір мүмкін мәніне кездейсоқ шамасының мүмкін мәндерінің жиыны, яғни статистикалық үлестіруі сәйкес болса, онда мұндай тәуелділік статистикалық тәуелділік деп аталады.
Анықтама 2
кездейсоқ шамасының 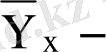шартты орташа мәні деп 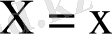болғандағы шамасының қабылдайтын мүмкін мәндерінің арифметикалық ортасын атайды.
Мысалы. болғанда мәндері:

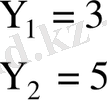
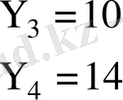
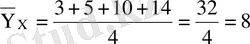
шартты орташа.
Анықтама 3
Егер бір кездейсоқ шама өзгергенде екінші кездейсоқ шаманың орта мәні өзгерсе, онда мұндай статистикалық тәуелділікті корреляциялық тәуелділік деп айтады. Сонымен және кездейсоқ шамаларының арасындағы корреляциялық байланыс мына формуламен беріледі

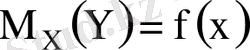(1.1)
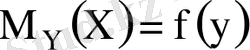(1.2)

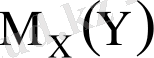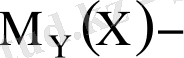, шартты математикалық үміттер. (1.1),(1.2) - моделдік регрессия теңдеулері деп аталады. Оларды табу үшін екі өлшемді кездейсоқ шаманың үлестіру заңын білу керек.

Жалпы регрессиялық моделдер. Регрессиялық модель жалпы түрде былай жазылады:

- кездейсоқ фактор.
Моделде кездейсоқ фактор болу себептері:
1) Моделге барлық түсіндіруші айнымалылардың кірмеуі.
Кез келген регрессиялық модель нақты жағдайдың жеңілдетілген түрі болып табылады.
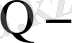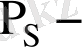Мысалы, тауарға сұраныс, тауардың бағасы, осы тауарды алмастырушы тауардың бағасы, 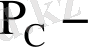осы тауарды толықтырушы тауардың бағасы, тұтынушының кірісі, тұтынушылар саны, тұтынушылар талғамы, тағы сол сияқты факторлар.
Бұл мысалда салт дәстұр, ұлттық және діни ерекшеліктері, географикалық орыны, ауа райы және көптеген факторлар есептелмейді, яғни

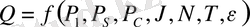
2) Моделдің функционалдық түрін дұрыс таңдай алмау, зерттелініп отырған процесті дұрыс білмеу немесе оның жиі өзгеруіне байланысты моделдеу функциясын дұрыс таңдай алмау.
3) Айнымалылардың күрделілігі. Көптеген моделдерде әрбір айнымалы күрделі бірнеше жай айнымалыларға тәуелді.
4) Өлшеу қателері. Модель қаншалықты сапалы болса да эмпирикалық мәліметтерге сәйкес келмейтін өлшеу қателері кездеседі.
5) Статистикалық мәліметтердің шектеулігі. Көбіне модель үздіксіз функция арқылы құрылады, ол үшін дискретті құрылымдағы мәліметтер қолданылады. Осындай айқыштық ауытқуына әсер етеді.
6) Адам факторын алдын-ала білмеу. Модель сапалы құрылса да, адам баласының ерекшеліктерін болжау мүмкін емес.
Зерттеу мақсатына және эмпирикалық мәліметтерге сәйкес сапалы регрессиялық модель құру күрделі және көп сатылы процесс. Оны үш сатыға бөлуге болады:
1) регрессия теңдеуінің түрін таңдау;
2) регрессия теңдеуінің параметрлерін анықтау;
3) регрессия теңдеудің сапалылығын талдау және моделдің эмпирикалық теңдеулеріне адекват екенін тексеру.h4

Қос сызықтық регрессия және регрессия теңдеуінің сапасын тексеру (Гаусс-Марков теоремасы және детерминация коэффициенті). Сызықтық регрессия моделі экономикалық айнымалылар арасындағы тәуелділікті көрсетеді және жиі қолданатын моделге жатады. Сызықтық регрессия тәуелді айнымалы- тің математикалық үміті және бір түсіндіруші айнымалы (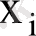- тәуелсіз айнымалының 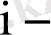ші бақылаудағы мәні ) арасындағы сызықтық функция.

(1.3)

Әрбір 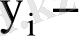дің оның математикалық үмітінен ауытқуын еске алып, (3) теңдеуін былай жазамыз
(1.4)

(1.4) - теориялық сызықтық регрессия моделі деп аталады; 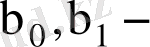регрессияның теориялық параметрлері (теориялық коэффициенттері); 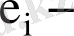кездейсоқ ауытқулар.
Жалпы түрде сызықтық регрессиялық модель былай жазылады

(1.5)

Сызықтық регрессиялық талдау есебі: және айнымалылары үшін белгілі статистикалық мәліметтер бойынша
а) 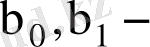коэффициенттерінің ең жақсы бағаларын табу;
ә) моделдің параметрлері туралы статистикалық болжамдарды тексеру;
б) статистикалық мәліметтермен модель қаншалықты үйлесімді, яғни берілген мәліметтерге модель адекват бола ма?
Көлемі шектелген таңдама бойынша сызықтық регрессияның эмпирикалық теңдеуін жазайық

(1.6)

мұнда шартты математикалық үміт бағасы, эмпирикалық коэффициенттер, белгісіз параметрлердің бағалары.
(1.7)

- ауытқуы теориялық кездейсоқ ауытқу 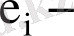дің бағасы. Бас жиынтық пен таңдаманың көлемдері әртүрлі болғандықтан ылғи да 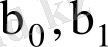-эмпирикалық коэффициенттердің 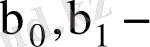теориялық коэффициенттерден айырмашылығы болады. Берілген таңдама мәліметтерін пайдаланып 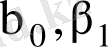коффициенттерінің бағаларын тауып, бақылау бойынша алынған нүктелер

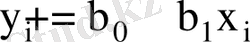
түзуіне жақын орналасатындай түзудің теңдеуін анықтау керек. Бір бас жиынтықтан алынған әртүрлі таңдамалар бойынша бір - бірінен айырмашылығы бар әртүрлі бағалар табылады.

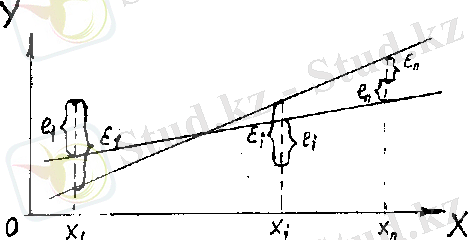
(1.1-сурет)

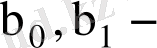коэффициенттерін табудың ең көп таралған және теориялық негізделген әдісі ең кіші квадраттар әдісі болып табылады. Бұл әдіс келесі қосындының минимум мәнін табуға негізделген және есептеуге ыңғайлы қарапайым әдіс.

1.3.Ең кіші квадраттар әдісі
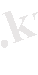
Берілген 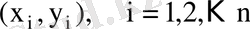таңдама бойынша регрессияның эмпирикалық теңдеуінің коэффициенттері 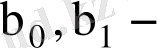ді анықтайық. Бұл жағдайда келесі функцияның минимум мәнін іздейміз.

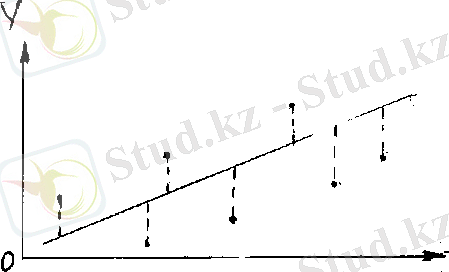
(1.2-сурет)

(1.8)

функциясы 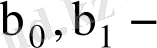параметрлерінің квадраттық функциясы, себебі () 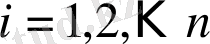бақылау бойынша белгілі сандар. Екі айнымалының функциясының экстремум мәні болуының қажетті шартын пайдаланып, функцияның 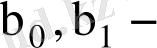белгісіз параметрлері бойынша алынған дербес туындыларын нөлге теңестірейік.

(1.9)

(1.10)

(1.10) жүйесінің теңдеулерін санына бөліп,

(1.11)

мұнда

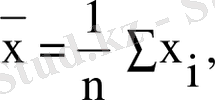
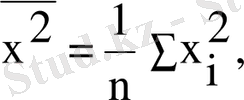
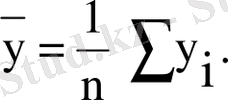
олай болса, ең кіші квадраттар әдісі бойынша белгісіз параметрлер бағасы 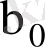және 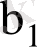(1,11) формулаларымен анықталады.

(1.12)

немесе

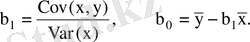
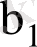коэффициентін түрлендіріп

(1.13)

мұнда 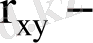таңдаманың корреляция коэффициенті;
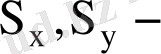стандарттық ауытқулар,
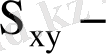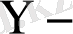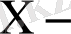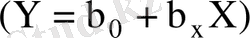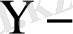таңдаманың ковариациясы. Олай болса, регрессия коэффициенті ковариация және корреляция коэффициенттеріне пропорционал. Ендеше корреляция коэффициенті белгілі болса, (1.13) формуланы пайдаланып қос сызықтық регрессия коэффициентін табуға болады. Егер тің ке регрессиялық теңдеуінен , осы эмпирикалық мәліметтер үшін тің ке регрессиялық теңдеуі (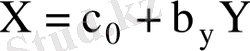) белгілі болса, онда

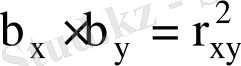
(1.14)

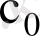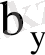және коэффициенттері келесі формуламен анықталады

(1.15)

Регрессия теңдеуінің сапасын тексеру. Ең кіші квадраттар әдісінің алғы шарттары (Гаусс-Марков шарттары)
1) барлық бақылаулар үшін кездейсоқ ауытқу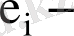дің математикалық үміті нөлге тең ;
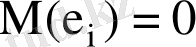2) кез келген 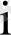және бақылаулары үшін кездейсоқ ауытқулар дисперсиясы тұрақты ;
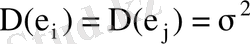3) кездейсоқ ауытқулар және, үшін бір-біріне тәуелсіз;
4) кездейсоқ ауытқулар түсіндіруші айнымалылардан тәуелсіз ;
5) модель параметрлер арқылы сызықтық тәуелсіз.

Гаусс-Марков теоремасы
Егер (1-5) алғы шарттар орындалса, онда ең кіші квадраттар әдісі бойынша табылған бағалар келесі қасиеттерге ие болады:
- бағалар жылжымаған болады, яғни
Бұл 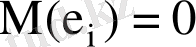шартынан шығады және регрессия түзуін анықтауда ұдайы қате жоқ екенін көрсетеді;
- бағалар орнықты, себебі бақылаулар саны өскенде бағалардың дисперсиясы нөлге ұмтылады
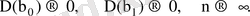
Басқаша айтқанда таңдаманың көлемі өсуіне байланысты бағалау дәлдігі өседі.
- баға тиімді, яғни параметрлердің басқа бағаларына қарағанда дисперсиясы ең кіші баға болып табылады.
Егер 2 және 3 алғышарттар орындалмаса, яғни ауытқулар дисперсиясы тұрақты емес және бір - бірімен байланысты болса, онда бағалар жылжымаған және орнықты болу қасиеттері сақталады, бірақ баға тиімді болмайды. Классикалық сызықтық регрессиялық модель құруда көрсетілген алғы шарттардан басқа бірнеше ұйғарым жасалады. Мысалы
- түсіндіруші айнымалылар кездейсоқ шама болмайды;
- кездейсоқ ауытқулар қалыпты үлестірілген;
- бақылаулар саны түсіндіруші айнымалылар санына қарағанда едәуір үлкен;
- спецификациялау қатесі жоқ;
- жетілген мультиколлинеарлық жоқ.
Сызықтық регрессия теңдеуінің коэффициенттерінің интервалдық бағасы. Ең кіші квадраттар әдісінің негізгі алғы шарттары математикалық үміті нөлге тең, дисперсиясы тұрақты ауытқуларының қалыпты үлестіруі туралы болжам болып табылады, яғни ~ 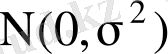. Бұл болжамның нақтылығы ықтималдықтар теориясындағы белгілі орта шектік теоремаға негізделген. Егер кездейсоқ шама көптеген (бірнеше) тәуелсіз кездейсоқ шаманың қосындысына тең және әрбір қосылғыштың қосындыға әсері шамалы болса, онда қарастырып отырған кездейсоқ шама қалыпты үлестіруге жатады. Бірақ кездейсоқ ауытқулары моделге кіргізілмеген тәуелсіз айнымалылардың шамаларына әсерін көрсетеді. Әдетте осындай айнымалылар саны өте көп, бірақ олардың жеке әсері өте аз. Сондықтан кездейсоқ ауытқуларды қарастыруда орта шектік теореманың шарттары толық орындалады деп айтуға болады. 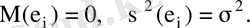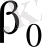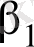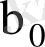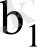кездейсоқ шамалары қалыпты үлестірілген деп тұжырым жасауға болады, яғни Онда ол тұжырым тек қана және сызықтық регрессия теңдеуінің және коэффициенттерінің сызықтық жылжымаған нүктелік бағалары ғана емес, сонымен қатар дәлдік кепілдігін беретін олардың интервалдық бағаларын табуға мүмкіндік береді. 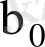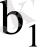Жоғарыда көрсетілген болжамдар, және кездейсоқ шамалары қалыпты үлестірілген деп айтуға мүмкіндік береді. Шынында да, бізге белгілі болғандай, қалыпты үлестірілген кездейсоқ шамалардың сызықтық комбинациясы қалыпты үлестірілген кездейсоқ шама деп айтуға болады. 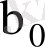және 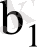мына түрде жазылуы мүмкін:

мұндағы 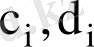- тұрақты сандар. Басқаша айтқанда, 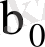және 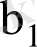, 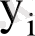арқылы -дің сызықтық функциялары болып табылады. Осыған сәйкес, 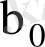және -де қалыпты үлестірілген. Алдында айтылғандай .

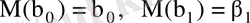(1.16)

мұнда . Ендеше,

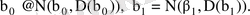
Жоғарыда көрсетілгендей статистика

(1.17)

еркіндік дәрежесі 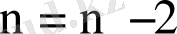, Стьюдент үлестіруі болады. Әрі қарай 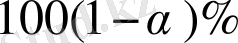- тік сенімділік интервалын табу үшін Стьюдент үлестіруінің кризистік нүктелер кестесінен сенімділік ықтималдығы 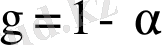және еркіндік дәрежесі 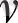болатын, мәні табылады.
(1.18)

(1.19)

(1.20)

Жақшадағы өрнекті түрлендіріп

(1.21)

(1.22)

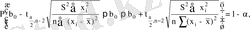(1.23)

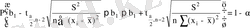. (1.24)

Қатынастар (), сенімділікпен және 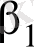параметрлерін жабатын сенімділік интервалдары:

(1.25)

. (1.26)

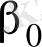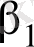Сенімділік интервалы регресияның және теориялық коэфициенттерінің табылған 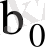және бағаларының 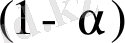сенімділігіне сәйкес болатын интервалды анықтайды.

1.4Детерминация коэффициенті
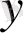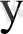Регрессияның әрбір коэффициентінің маңыздылығын тексергеннен кейін әдетте оның регрессия теңдеуінің жалпы сапасы тексеріледі. Егер барлық нүктелер құрылған теңдеудің бойында жататын болса, онда -тің -ке тәуелділігі -тің мәндерінен байқалады. Регрессия теңдеуінің жалпы сапасының қосындылық өлшемі - детерминация коэффициенті.

(1.27)
Коэффициенттің мағынасын түсіндірейік. Регрессияның эмпирикалық теңдеуі:
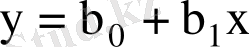. (1.28)

Бақыланған нақты мәндері 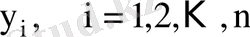; модель бойынша мәндері 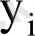, ауытқуы шамасы
. (1.29)

Бұл өрнекті
(1.30)

немесе
,

-бақыланатын 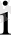-ші нүктенің тәуелді айнымалының орташасы 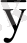-тен ауытқуы; 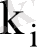- регрессия түзуіндегі осы нүктенің 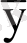-дан ауытқуы; -осы нүктенің модель бойынша регрессия теңлеуімен анықталған 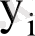мәнінен ауытқуы. Барлық ауытқулар тәуелді айнымалының өсі бойынша есептеледі.

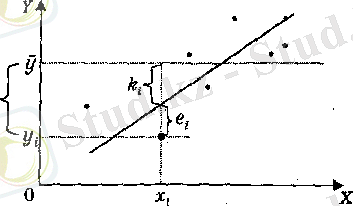
(1.3-сурет)

(1.31)

, онда келесі қатынас орындалады

(1.32)

Соңғы теңдеу жалпы квадраттар қосындысы, яғни 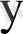-тің қарағанда бытырап орналасуының өлшемі деп қарастыруға болады.

түсіндіруші квадраттар қосындысы.
қалдық квадраттар қосындысы.

(1.32) теңдігін сол жағындағы қосындыға бөліп,

(1.33)

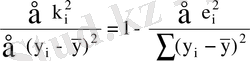
Белгілеу енгізетін болсақ
, ендеше (1.34)

Ⅱ Бөлім
Регрессиялық модель құру
2.1.Құмдық коэффинцентін есептеу
Мұнай мен газ қорын болжаудың негізгі параметлерінің бірі пластардың және пропласклардың қосындысына тең аралық болып табылады. Бұл аралық әдетте қандайда бір коэффицентті перспективті комплекстің жалпы қабатына көбейтіндісімен есептеледі.Бұл коэффицентті құмдық коэффицент деп аталады.Әрине бұл коэффицент әр түрлі аймақ үшін әр түрлі мәнге ие болады. Айтылғанды математикалық түрде жазатын болсақ:
he=aH0
Бұл жердегі he-комплекстің жалпы әсерлі қабаты; H0-комлекстің жалпы қабат; a-құмдық коэффиценті.
Бідің математикалық моделімізде бос мүше бола алмайды. Себебі H0=0 болғанда he=0 болуы қажет.
Мұнай қорларына болжам жасау үшін бізге құмыдқ коэффиценттің шамасын білу қажет.
Орта квадраттық ауытқуы минумум болғанда құмдық коэффицентін есептейік
i=1NHei-hei2= i=1NHei-aH0i2=min, (2.1)

(2)
Мұндағы Hei-қабат қалыңдықтарының нақты мәндрі
i=1NHei-aH0iH0i=0 (2.2)
Осыдан
a=i=1NHeiH0ii=1NH0i2 (2.3)

Кесте 1
Сызқты корреляциялық модельдің параметрлерін есептеу
Аудан, ұңғыма
Hei,км
H0i,км
HeiH0i
H0i2
hei, км
Hei-hei
Hei-hei2
Қызан
Кокбахты
Сарга
Кумтобе
Байтерек
Чагырлы
Тереңқұдық
Буранкуль
Прорва
Шахпахты, 2
Барса-Келмес
Узень
Жетыбай
Шахпахты, 1
Кармандыбас
0,05
0,13 0,12 0,14 0,20 0,20 0,20 0,28 0,29 0,30 0,33 0,34 0,33 0,36 0,36
0,12
0,32 0,48 0,55 0,51 0,58 0,64 0,83 0,99 0,82 0,99 1,02 1,10 1,10 1,32
0,01
0,04
0,06
0,08
0,10
0,12
0,13
0,23
0,29
0,25
0,33
0,35
0,36
0,40
0,48
0,01
0,10
0,23
0,30
0,26
0,34
0,41
0,69
0,98
0,67
0,98
1,104
1,21
1,21
1,74
0,04
0,09
0,15
0,17
0,16
0,18
0,20
0,26
0,31
0,25
0,31
0,32
0,34
0,34
0,41
0,01
0,04
-0,03
-0,03
0,04
0,02
0
0,02
-0,02
0,05
0,02
0,02
-0,01
0,02
-0,05
0,0001
0,0016
0,0009
0,0009
0,0016
0,0004
0
0,0004
0,0004
0,025
0,0004
0,0004
0,0001
0,0004
0,0025
Σ
3,63
11,37
3,23
10,17

0,0126

Кестеде корреляциялық модельдің параметрлерін есептеп көрсетілен. Осы кестені пайдаланып регрессияның коэффицентін бағалауға болады. (2.3) - ті пайдаланып
a=3,2310,17≈0,31 ,
Жалпы тиімді қуттың математикалық үміті
He= 3,6315≈0,24 км

Жалпы қуаттың математикалық үміті
H0=11,3715≈0,76 км
Дисперсия ауытқуы
he=0.31H0
s2=0,012615-2≈0,001 км2
Осыдан
s≈0,03 км

Кесте 2
Корреляция коэффиценттерін есептеу
Hei,
H0i
Hei-He
H0i-H0
Hei-He2
H0i-H02
(Hei-He)x(H0i-H0)
0,05
0,13
0,12 0,14 0,20 0,20 0,20 0,28 0,29 0,30 0,33 0,34 0,33 0,36 0,36
0,12
0,32 0,48 0,55 0,51 0,58 0,64 0,83 0,99 0,82 0,99 1,02 1,10 1,10 1,32
-0,19
-0,11
-0,12
-0,10
-0,04
-0,04
-0,04
0,04
0,05
0,06
0,09
0,10
0,09
0,12
0,12
-0,64
-0,44
-0,28
-0,21
-0,25
-0,18
-0,12
0,07
0,23
0,06
0,23
0,26
0,34
0,34
0,56
0,0361
0,0121
0,0144
0,0100
0,0016
0,0016
0,0016
0,0016
0,0025
0,0036
0,0081
0,0100
0,0081
0,0144
0,0144
0,4096
0,1936
0,0784
0,0441
0,0625
0,0324
0,0144
0,0049
0,0529
0,0036
0,0676
0,1156
0,1156
0,3136
0,1216
0,0484
0,0336
0,0210
0,0100
0,0072
0,0048
0,0115
0,0036
0,0207
0,0260
0,0306
0,0408
0,0672

Σ
0,1401
1,5617
0,4498

2.2.Корреляция коэффицентін бағалау
Корреляция коэффицентін бағалау үшін кеcтені пайдаланайық
r=0,44980,1401∙1,5617≈0,96
Демек, тиімді және жалпы қуаттардың арасында тығыз сызықты байланыс бар.
Анықталған параметрлердің сенімділік интервалын анықтайық
0,31-1,771*0,0011.5617=A=0,31+1,7 71*0,0011,5617
0,31-0,044=A=0,31+0,044
0,266=A=0,354
Дисперсияны бағалау сенімділік интервалы
0,001∙(15-2)19,81=σ2=0,001∙(15-2) 7,04
0,0007=σ2=0,0018
hei мәндерінің сенімділік интервалын табайық
Егер
H0=0,5 км he=0,31∙0,5=0,155 км. болса
α=1 деп алсақ
0,155-1,771∙0,03115+0,5-0,7621,5617 =He0,5==0,155+1,771∙0,03115+0,5- 0,7621,5617
Осыдан
0,137=He(0,5)=0,173.

Егер
H0=1,0 км he=0,31∙1,0=0,31 км, болса
Онда
0,293=He(1,0)=0,327

t=r1-r2N-2-статистикалық критерий (2.4)
Пайдаланып
t=0,961-0,96215-2≈12,16
13-дәрежелі босаңдықта 90 пайыздық ықтималдық үшін t-ның кестелік мәні 1,771 ге тең.

t≫t0.05;13, болғандықтан

тиімді және жалпы қуаттардың арасында байланыс бар деп айта аламыз.
Сенімділік интервалын оңайырақ жолмен есептеп табуға болады. Ол үшін келесі формуланы пайдаланамыз
sa2=sY2sX21-r2N-3 (2.5)
Осыдан шығады:
sa2=0,14010,15617(1-0,96215-3)≈0.00 06
sa≈0,025
Есептеп тапқан регрессия коэффицентіміз a=0,31 сенімді деп айтуға болады. Себебі,
0,31≫3∙0,025
Коррелляция коэффицентін бағалау үшін келесі формуланы пайдаланамыз
sr2=1-r22N (2.6)
Егер,
r3sr (2.7)
болса, онда бағалау (корреляция коэффицентін) сенімді деп айта алмыз

Олай болса
sr2=(1-0,962)2N≈0,0004
sr≈0,02
0,96=3∙0.02 , болғандықтан
Корреляция коэффиценті жоғары сендімділікке ие деп айта аламыз.
Қорыта айтқанда құрастырған моделіміздің сенімділік деңгейі жоғары және болжам жасау үшін пайдалануға болады деген қорытындыға келеміз. Алайда бұл регрессия моделі тек Арал-Каспий мұнай өндіру секторына ғана жарамды екенін айта кеткен жөн

Ⅲ.Бөлім
Мұнай бағасының өзгерісн зерттеу
3.1.Мұнай бағасының өзгеруіне әсер ететін факторлар
Мұнай бағасының өзгеруіне әсер ететін факторларды сыртқы(технологиялар, негізгі мұнай өндіруші елдердегі жағдай) және ішкі(елдегі экономикалық жағдай, политикалық, метеорологиялық) деп 2-ге бөліп қарастыруға болады.
Бағаға ең үлкен әсер етуші фактор бүкіләлемдік экономиканың дамуы деп санаған жөн, және ЖІӨ (жалпы ішкі өнім) өзгеріс қарқындылығы; ғылыми техникалық даму (жаңа технологиялар, материалдар, байланыс құралдары және т.б.); мұнай қорларының бар болуы және болжануы, альтернатифті энергия көздерінің бағасы. Мұнайға байланысты заңдардың өзгерісі. Валюта бағамының өзгерісі жәек т.б.
Қазіргі таңда мұнай бағасының өзгерісіне әсер ететін ең негізгі фактор ол ЖІӨ - нің өсуі болып табылады. ЖІӨ - нің өсуі мұнайға деген сұранысты арттырады.
Мұнайға деген сұраныстың артуына оның әлемдік бағасының деңгейі қатты әсер етеді. Мұнай бағасының жоғары болуы басқа альтернативті энергия көздерінің бәсекеге қабілеттілігін арттырады.Бұл мұнайды басқа энергия көзімен ауыстуға әкеледі (мысалы газ, электр энергиясы және т.б.). Нәтижесінде мұнайға деген сұраныстың төмендеуіне әкеледі. Сұраныстың пайда болуына біршама әсер ететін фактор ол климаттық жағдай, ең алдымен температура өзгеріс. Қысқы мерзімде температура төмен болса мұнайға деген сұраныс сол аралықта артатынын байқауға болады. Себебі, мұнай өнімдерін уйлерді жылытуға көптеп пайдаланылатындықтан мұнайға деген сұраныс артады. Және керіснше қыс жылы болса мұнай өнімдеріне деген сұраныс төмендейді.
Ғылыми техникалық жетістіктер мұнай өндірісінде жұмсалатын шығындарды, тасымалдауға, сақтауға кететін шығындарды азайтады. Бұл мұнай бағасының төмендеуіне әсер етеді.
Мұнай қорларының таусылуы оның бағасының артуына әсер етеді. Ал мұнай қорларының жаңа көздерінің ашылуы керісінше мұнай бағасының төмендеуіне әкеледі.
Алайда соңғы жылдары мұнай қорларының таусылуы оның бағасының өзгеруіне айтарлықтай әсер етіп жатқан жоқ. Себебі, мұнай қорларының таусылуы жайлы ақпараттармен қоса жаңадан табылып жатқан мұнай көздері туралы ақпараттар аз емес. Соған байланысты Халықаралық энеогетикалық агенттіктердің хабарлауы бойынша мұнай әлі ұзақ уақыт өндірілетін болады.
Бағаға әсер етуші факторлардың тізімі уақыт өте келе өзгеруі мүмкін. Ең алдымен мұнай бағасының өзгеріуі саясы жағдайларға байланысты болмауы мүмкін. Егер бұрын АҚШ әскерінің Ирак жеріне кіру мүмкіндігі жайлы ақпараттар мұнай биржасында көптеген толқулар шақыратын болса, қазір мұндай хабарлар мұнай бағасының өзгеруіне еш әсер етпейді.
Мұнай бағасының өзгеруіне әкелетін факторлардың біріне қаржы ұйымдарының әсері артуын атап өтен жөн. Оларға банктер, инвестициялық компаниялар жатады. Бұл қаржылық уйымдар үлкен мұнай компанияларының құнды қағаздарын көптеп сатып алған. Сондықтан олрға мұнай бағасының жоғары болуы тиімді.
2007 жылы Эр-Риядта өткен ОПЕК-ке мүше елдердің 3-самитінде мұнай рыногы қазіргі таңда ОПЕК территориясында емес деген қорытындыға келген болатын. Біршама зерттеулер нәтижесінде саметке қатысушы мүшелер мұнай бағасының қалыптасуына қаржылық факторлар ең көп әсер етеді деген қорытындыға келген болатын.
Мұнай бағасы мен альтернативті энергия көздері арасындағы байланысқа мән беру керек. Бұл әлемде әртүрлі өзгерістер (экологиялық, экономикалық және т.б) болуымен сиппатталады.Осындай өзгерістердің бәрі энергия көзін таңдауға әсе етеді.Мысалы, қазіргі таңда эеомикасы жақсы дамыған елдер экологиялық таза энергия көздеріне көшуге тырысып жатыр, ал дамушы елдер керіснше мұнай мен мұнай өнімдерін пайдалануын арттыруда (арзан энергия көздері).
Осы бөлімде қарастырылған мұнай бағасына әсер етуші факторлард келесі кестеде көрсетуге болады. (кесте 1).
Кесте 3.
Мұнай бағасының қалыптасуына әсер етуші факторлар
Бағаның төмендеуі
Бағаның өсуі
Ғылыми техникалық прогресс
Альтернативті энергия көздерінің ашылуы
Мұнай қорларынң көбеюі
Жылы қыс мезгілі

ЖІӨ өсуі
Әскери қақтығыстар
Мұнай қорларының азаюы
Суық қыс мезгілі

3.2. Мұнай бағасын болжау әдісі

Мұнай бағасының күрт өзгерісі мұнай импорттаушы және өндіруші елдердегі жағдайға кері әсер етеді деген плірлер бар. Мұнай бағасын дәл болжау әртүрлі мамандықтағы адамдардың қызығушылығын тудырады. Мысалы банк қызметкерлері болжанған мәліметтерді макроэкономикалық болжамдар жасау үшін пайдаланады.
Сонымен қатар экономиканың кейбір секторлары мұнай бағасының болжамына тікелей қатысы бар. Мысал ретінде авиакомпанияларды алсақ болады,олар мұнай бағасының болжамына қарап билет құнын есептейді.
Кез келген экономикалық көрсеткішке бір ғана емес, көбінесе бірнеше факторлар әсер етеді. Мысалы, кейбір тауарға сұраныс тауар бағасымен ғана емес, басқа оны алмастыратын және толықтыратын тауарлармен, тұтынушы табысымен және көптеген басқа факторлармен анықталады. Бұл жағдайда екі айнымалының сызықтық регрессиясының заңды жалғасы - регрессия моделі қарастырылады. Яғни, регрессиялық талдау (статистикалық тәуелділік және жалпы регрессиялық модельдер) және моделде кездейсоқ фактор болу себептерін, қос сызықтық регрессия және регрессия теңдеуінің сапасын тексерудегі Гаусс-Марков шарттарын және детерминация коэффициентін, сызықтық регрессиялық талдау есебін және ең кіші квадраттар әдісін түсіну.
Осы жұмыстың практикалық бөлігіне мұнай бағасы ретінделя Brent маркалы мұнай алу шешілді. Brent (Brent Crude) -- Солтүстік теңізде өндірілетін эталонды мұнай маркасы. Марканың аты 1970 жылы Солтүстік теңізде ашылған аттас мұнай өндіру орнынан алынған.
Мұнай мен альтернативті энергия көздерінің(газ және көмір) 2000 жылдан 2015 жылға дейнгі бағасы алынды. Біз мұнайға альтернативті энергия көзі ретінді газ бен көмірді алдық. Себебі бұлар қазіргі таңда нарықта сұранысқа ие энергия көздері болып табылады. Жәнеде мұнай бағасының алтернативті энергия көздеріне қаншалықты әсер ететінін білгіміз келді.Тағы бір айнымалы ретінде алтын алынды. Себебі, мұнай бағасы алтын бағасына әсерін білгіміз кеді. Сонымен қатар алытын инвестиция көзі ретінде пайдаланылады.
Бұл жұмыста біз қосымша айнымалылар ретінде таяу шығыстағы әскери қақтығыстарды алдық. Айнымалы ретінде әскери қақтығыстарды алу себебіміз, осы қақтығыстар мұнай бағасының өзгеуіне әсер етуін немесе ісер етпеуін білгіміз келді.Тағы бір қосымша айнымалы ретінде жылы болғаң әлемдік дағдарысты алдық. Өйткені сол дағдарыс кезінде мұнай бағасының күрт өзгерісі байқалған болатын.
Кесте 4
Айнымалылар сипаттамасы
Фактор
Айнымалы
Brent маркалы мұнай бағасы
Алтын бағасы
Көмір бағасы
Газ бағасы

BP(Brent Price)
Gold
Coal
Gas
Қосымша айнымалылар:
Әлемдік дағдарыс
Әскери Қақтығыс
(Палестина - Израель)

MFC
pal_isr

2 кестеде біздің моделімізге қосқан барлық айнымалыларымыз көрсетілген. Кестенің оң жағында Eviews бағдарламасында әр айнымалы қалай белгіленгені көрсетілген .
Дерек көзі ретінде келесілер пайдаланылды: BP Statistical Review of World Energy June 2016, Index Mundi.
Деректерді талдап эконометрикалық модель құрмастан бұрын алдымен статистикалық мәліметтерді қарап шығайық. Мұнай бағасының статистикалық деректерінен бастайық.

Сурет 2.1. Мұнай бағасынынң гистограммасы
Мына гистограммада көрініп тұрғандай, 1 суретте корсетілген, BP айнымалысы үшін математикалық орта мән 57,53-ке тең. Бұл мұнайдың бағасының орта мәні 58 долларбаррель маңайында екенін көрсетеді.
Қатарды тұрақтылыққа тексерейік
Кесте 5
Мұнай бағасының стационарлығын тексеру
Test
t-Statistic
Prob.
Augment Dickey-Fuller test statistic
-1.396635
0.5831
Қатар стационар емес (3 кестеге қараймыз), ықтималдық көрсеткіші Prob=0.5831. Қатарды стационарға айанлдыру үшін оның алғашқы айырмасын тексеіп көрейк.

Кесте 6
Мұнай бағасының стационарлығын тексеру
Test
t-Statistic
Prob.
Augment Dickey-Fuller test statistic
-10,35390
0.0000
4 кестедегі нәтижеге сәйкес бізге қатарды стационар түрге келтире алдық.

Енді осындай статистикалық тексерулерді басқа айнымалылар үшін де жасап көрейік: көмір, газ және алтын үшін.

Сурет 2.2. Көмір бағасының гистограммасы
Сурет 2 дегі гистограмманы қарап шықсақ айнымалы COAL үшін орта мән 58.84 ке тең, демек көмір бағасының орта мәні 59 аумағында деген сөз. 5 кестеде корсетілшен мәліметке қарасақ, қатардың стационар екенін байқаймыз.

Кесте 7
Көмір бағасының стационарлығын тексеру
Test
t-Statistic
Prob.
Augment Dickey-Fuller test statistic
-7,768911
0.0000

Келесі газ бағасын тексерейік

Сурет 2.3 Газ бағасының гистограммасы
3 суретте көрсетілген гистограммадан біз GAS айнымалы бағасының орта мәні 178.15 ке тең екенін көреміз. Демек газ бағасы ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.