Санның бүтін және бөлшек бөлігіне берілген теңдеулерді шешу әдістері

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 45 бет
Таңдаулыға:

Қазақстан Республикасы Білім және ғылым министрлігі

Х. Досмұхамедов атындағы Атырау мемлекеттік университеті

Математика және математиканы оқыту әдістемесі кафедрасы

«Қорғауға жіберілді»

Кафедра меңгерушісі

Н. Қ. Шаждекеева

« »2019 ж.

ДипломДЫҚ жұмыс

Тақырыбы: «Санның бүтін және бөлшек бөлігіне берілген олимпиадалық есептерді шешу әдістері»

5В010900- «Математика» мамандығы бойынша

Орындаған: Аманқос А. Қ.

Ғылыми жетекшісі:

п. ғ. к., профессор Тұржігітова Ғ. Ж.

Норма-бақылаушы: Балтурганова С. К.

Атырау 2019

МАЗМҰНЫ

Кіріспе

: 1

Кіріспе: САННЫҢ БҮТІН ЖӘНЕ БӨЛШЕК БӨЛІГІ, ГРАФИКТЕРІ ЖӘНЕ ҚАСИЕТТЕРІ

3: 7

: 1. 1

Кіріспе: Санның бүтін бөлігі, оның графигі және қасиеттері

3: 7

: 1. 2

Кіріспе: Санның бөлшек бөлігі, оның графигі және қасиеттері

3: 15

Кіріспе: 1 тарау қорытындысы

3: 28

Кіріспе:

: 2

Кіріспе: САННЫҢ БҮТІН ЖӘНЕ БӨЛШЕК БӨЛІГІНЕ БЕРІЛГЕН ОЛИМПИАДАЛЫҚ ЕСЕПТЕРДІ ШЕШУ ӘДІСТЕРІ

3: 29

: 2. 1

Кіріспе: Санның бүтін және бөлшек бөлігіне берілген теңдеулерді шешу әдістері

3: 29

: 2. 2

Кіріспе: Санның бүтін және бөлшек бөлігіне берілген теңсіздіктерді шешу әдістері

: 2. 3

Кіріспе: Санның бүтін және бөлшек бөлігіне берілген теңдеулерді шешудің функционалды-графиктік әдісі

: 2. 4

Кіріспе: Педагогикалық тәжірибе

Кіріспе: 2 тарау қорытындысы

Кіріспе: ҚОРЫТЫНДЫ

Кіріспе: ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ

КІРІСПЕ

Тақырыптың өзектілігі. Адамзаттың ілгері дамуы үшін, білім мен ғылымның, техникалық өрлеудің маңызы зор. Адам өміріндегі ғылымның орны мен рөлін түсіну осы уақытқа дейін аяқталмаған күрделі процесс. Қазіргі ғылым мен техниканың қарыштап өсуі мен ел экономикасының қарқынды даму үстіндегі кезеңде адамдардың көзқарасының заман талабына сай өзгере бастағаны олардың өмір сүру дәстүрінен анық байқалады. Бұл-әлемді қамтыған жаhандану дәуірінің бастапқы көрінісі.

Білім беру жүйесі-әр елдің даму болашағын айқындайтын, әлемдік өркениетке жетуде негізгі бағыттарын көрсететін біртұтас құрылым.

Білім беру жүйесінің даму деңгейі мен сапасы елдегі педагогика ғылымының жетістігімен байланысты. Бұл өз кезегінде экономикалық және ғылыми-техникалық дамудың, яғни мемлекет пен қоғамның табысты дамуының кепілі болып табылады.

Қазіргі кездегі шапшаң жүріп жатқан жаhандану үрдісі әлемдік бәсекелестікті күшейте түсуде. Қазақстан Республикасы жалпы білім берудің жүйесін жетілдірудің жаңа кезеңіне қадам басты. Білім берудегі басты мақсат-жан-жақты дамыған, білімді, өмір сүруге бейім, өзіндік ой-толғамы бар, адамгершілігі жоғары, бәсекеге қабілетті жеке тұлғаны тәрбиелеу.

XIX ғасыр-білім ғасыры. Болашақтың бүгіннен де нұрлы болуына ықпал етіп, адамзат қоғамын алға апаратын құдіретті күш тек білімде ғана.

Білімнің іргетасын қалайтын негіздері мен танымдық қызығушылығы, жеке-дара шығармашылық жұмысқа деген дағдылары қалыптасатын мектептің білім беру саласындағы рөлі зор. Соған байланысты оқу-тәрбие үрдісін жақсартып, оқытуда жаңа педагогикалық технологияларды кеңінен қолдана отырып білімді терең игерудің жолдарын, әр пәннің ғылыми негіздерін меңгерту мәселелерін, оқушының ойлау қабілеті мен шығармашылық әрекетін дамыту сияқты ұтымды түрлеріне сүйенгеніміз жөн. Ондай істерді атқарғанда жалаң еліктеуді болдырмас үшін дәстүрлі тәжірибелерімізбен бірге әлемдік игі мұраларды сәйкестендіріп қолдансақ, оқу-тәрбие үрдісін бүгінгі күннің талаптарына сәйкес жүргізер едік. Сапалы білім беру үздіксіз ізденумен тығыз байланысты.

Білім алуда әрбір жеке тұлға өзінің танымдық және шығармашылық іс-әрекетін шыңдауы қажет. Оның бастапқы айқын жолы ғылыми шығармашылық ізденіс екені белгілі.

Кез келген мемлекетің рухани және әлеуметтік дәрежесі білім деңгейіне байланысты бағаланады, сондықтан да, білім өркениеттіліктің әрі өлшемі, әрі тетігі болып табылады.

Еліміздің білім беру жүйесінің даму жолындағы көкейтесті мәселелердің бірі, заман талабына сай білім сапасын арттыру, әлемдік стандарт дәрежесіндегі білім беру болып табылады. Еліміздің әлемдегі бәсекеге қабілетті 50 елдің қатарына енудің басты міндеті, жоғарғы мамандандырылған, білікті адамзат ғылыми технологияны жеңіл меңгеріп, нарық экономикасында өз-өзін басқара алатын және алған білімін тұрмыста пайдалана алатын болса, онда тек сол кезде ғана жүзеге асыру мүмкін екендігі белгілі.

Расында да, әлемнің озық дамыған елдеріндегі білім беру жүйесі-ақпараттық интеллектуалды ресурстарды өз бетінше іздеп, талқылап және оны қолдана білетін, жедел техникалық ілгерілеу, инновациялық өрлеу жағдайында өзін-өзі айқын көрсете алатын, нарықтық талаптарға еркін бейімделе алатын жеке тұлғаны қалыптастыруға басымдық беретіндігі белгілі.

Бүгінгі таңда кез келген қоғамға дарынды адамдар керек, бұл кезекте қоғамның міндеті сондай дарынды адамдардың қабілетін одан әрі дамыту. Өкінішке орай, көп жағдайларда кез келген адам өз дарынын дұрыс аша алмайды. Бұның бәрі отбасына да, мектепке де тікелей байланысты. Бұл кезекте отбасының міндеті баланың дарынын ертерек ескеру болса, мектептің міндеті баланы қолдап, сол дарынын әрі қарай ашуға және дамытуға жол көрсету болып келеді. Оқушылардың шығармашылық негізінің қалыптасуына, мектеп мұғалімінің үлесі зор. Кез келген мұғалім терең ғылыми кітаптарды, энциклопедияларды оқитын, өздігінен ізденіп, әр түрлі салада өз сұрақтарына жауап іздей білетін дарынды оқушыға жолығады. Сондықтан да, оқушыға бағыт беру, оның армандары мен өмірлік жоспарларына көмектесу мектепте жүзеге асырылуы қажет. Мұндай оқушыларды әр түрлі ғылыми-шығармашылық жұмыстарға, олимпиадаларға, сайыстарға қатыстыру керек. Осылайша оқушының қабілетімен зеректігін көсетуге мүмкіндік туады. Оқушыларды жеке тұлға етіп тәрбиелеуде математика пәнінің алатын орны ерекше, салмағы зор.

Оқушылардың мектептегі математика пәні мазмұнын жан-жақты зерттеп, орынды қолдану олардың жалпы, білімінің, мәдени даму деңгейінің жоғары болуына тікелей әсер ететіні сөзсіз. Математика сабағында есеп шығару оқыту үрдісінің ең маңызды бөлігі болып табылады. Өйткені, есеп шығару арқылы оқушы математикалық теорияны меңгеріп қана қоймай, оның логикалық ойлауы мен шығармашылық қабілеті дамиды.

Санның бүтін және бөлшек бөліктері ұғымы математикамен айналысатын адамдарды әрдайым қызықтырып келген. Оларды танып-білуге, зерттеуге арналған еңбектер көп. Санның бүтін бөлігі түсінігін неміс математигі Иоган Карл Фридрих Гаусс (1771-1855 ж. ж. ), сандар теориясы бойынша еңбектердің авторы енгізді. Сонымен қатар Гаусс арнайы функциялар теориясын, қатарларды, сандық әдістерді, математикалық физиканың есептерін шешуді алға тартып, потенциалдың математикалық теориясын жасады. $x$ нақты санының бүтін бөлігін $\lbrack x\rbrack$ таңбасымен белгіленуді Карл Гаусс 1808 жылы енгізді.

Санның бүтін бөлігінің функциясын француз математигі Адриан Мари Лежандр (1752-1833 ж. ж. ) енгізді. Оның 1798 жылы жарыққа шыққан "сандар теориясының тәжірибесі" еңбегі, XVIII ғасырдың арифметикалық жетістіктерінің іргелі қорытындысы болып табылады. Дәл оның құрметіне $y = \lbrack x\rbrack$ функциясын француздың "Антье" сөзімен (фр. "entier" - бүтін) $E(x)$ атады.

Санның бүтін және бөлшек бөлігіне берілген есептерді шешу шығармашылықты, білімнің тереңдігін талап ететін дүниелердің бірі. Сонымен қатар оқушыларды сандар әлемі қызықтырады, әрі терең ойландырады. Санның бүтін және бөлшек бөліктеріне берілген теңдеулер мен теңдеулер жүйесінің шешімдері бар ма, болса, оның түбірлерін қалай табуға болады деген сұраққа жауап ізделінеді.

Мәселенің зерттелу деңгейі: Олимпиадалық есептерді шығару әдістері мен жолдары көптеген педагогтардың, ғалымдардың, әдіскерлердің: Колмогоров А. Н., Шарыгин И. Ф., Гусев В. А., Агаханов Н. Х., Терешин Д. А., Фарков А. В., Галкин Е. В., Гальперин Г. А., Құрманалин Х. М., Күнғожин А. М., Байсалов Е. Р., Елеусізов Д. А., Ырысбек М., И. Р. Высоцкий, Ю. А. Цимбалов, И. Яковлев, И. В. Ященко еңбектерінде келтірілген. [1]

Алайда, санның бүтін және бөлшек бөлігіне берілген олимпиадалық есептерді шешу жолдары жеткіліксіз зерттелгендігінен, осы тақырып зерттеуге таңдалып алынды.

Бұл зерттеу жұмысымызда мектеп оқушыларының математикалық олимпиадаларында кездесетін санның бүтін және бөлшек бөлігіне берілген олимпиадалық есептерді шешудің әртүрлі тәсілдері көрсетіледі.

Осы айтылғандар біздің зерттеу жұмысымыздың көкейкестілігін анықтап, зерттеу тақырыбын «Санның бүтін және бөлшек бөлігіне берілген олимпиадалық есептерді шешу әдістері» - деп тұжырымдауға негіз болды.

Зерттеу мақсаты: математикалық олимпиадаларда кездесетін санның бүтін және бөлшек бөлігіне берілген есептерді шешудің әдіс - тәсілдерін жүйелеп, сұрыптау және жиі қолданылатын негізгі тәсілдерін көрсету.

Зерттеу нысаны - орта мектептегі математика курсын оқыту үрдісі.

Зерттеу пәні: оқулықтардағы және әр түрлі деңгейдегі математикалық олимпиадаларда кездесетін саннің бүтін және бөлшек бөлігі тақырыбына берілген есептер.

Зерттеу міндеттері :

а) зерттеу тақырыбы бойынша математикалық, әдістемелік әдебиеттерді оқып, танысу

ә) санның бүтін және бөлшек бөлігіне берілген олимпиадалық есептерді шешудің тиімді әдіс - тәсілдерін талдап, жүйелеу

б) педагогикалық эксперимент бөлімінде «Санның бүтін және бөлшек бөлігіне берілген олимпиадалық есептерді шешу әдістері» атты арнайы курсты дайындау.

Мәселенің деректік көзі: зерттеу проблемасы бойынша педагогтардың, математик-әдіскерлердің еңбектері, мектеп оқулықтары, математикалық олимпиадаға арналған әдістемелік әдебиеттер, математикалық интернет сайттар.

Зерттеудің әдістері, әдіснамалық негіздері: Математикалық олимпиадаларға арналған оқу-әдістемелік құралдарды оқу, зерттеу, жүйелеу және зерделеу, тәжірибелік-әдістемелік жұмыстарды жүргізу.

Зерттеудің жетекші идеясы: олимпиадалық есептерді шешуді үйрету арқылы оқушылардың математикаға қызығушылығы мен ынтасын арттырып, оқу сапасын жақсартуға болады.

Практикалық маңыздылығы: зерттеу нәтижелерін әдістемелік құралдарды дайындағанда, математиканы оқыту барысында оқушылардың ой-өрісін дамытуда, мектеп мұғалімдерінің білімін жетілдіру курстарында пайдалануға болады. Дайындалған арнайы курс жоспарын мектеп мұғалімдері өздерінің күнделікті іс-тәжірибелерінде қолдана алады.

Диплом жұмысының мақұлдануы. Диплом жұмысының негізгі мәселелері математика және математиканы оқыту әдістемесі кафедрасының отырысында және 2019 жылдың 12 сәуірінде өткен «Білім беру мазмұнын жаңарту жағдайында педагогикалық кадрларды кәсіби даярлау: құзыреттілік, технология, инновация» тақырыбындағы Республикалық ғылыми-әдістемелік конференциясында осы тақырып бойынша баяндама тыңдалып, мақұлданды.

Диплом жұмысының құрылымы. Диплом жұмысы кіріспеден, екі тараудан, қорытындыдан, пайдаланылған әдебиеттер тізімінен тұрады.

САННЫҢ БҮТІН ЖӘНЕ БӨЛШЕК БӨЛІГІ, ГРАФИКТЕРІ ЖӘНЕ ҚАСИЕТТЕРІСанның бүтін бөлігі, оның графигі және қасиеттері

Математика пәнінен олимпиадаға қатысқан оқушылар санның бүтін және бөлшек бөлігі ұғымдарына берілген есептерді шығару кезінде қиындықтарға тап болады. Мысалы, математикалық олимпиадаларда мынадай есептер кездеседі:

$5\lbrack x\rbrack + 27\left\{ x \right\} = 2012$ теңдеуінің түбірлерінің санын табыңдар, мұнда $\lbrack x\rbrack\$ - $x$ санының бүтін бөлігі, ал $\{ x\}$ - $x$ санының бөлшек бөлігі.

Оқушылар санның бүтін және бөлшек бөлігі туралы материалдарды зерделеп, осы тапсырманы орындай алады.

Бұл тақырып олар үшін теориялық және практикалық тұрғыдан қиындықтар тудырғандықтан, осы тақырыпты түсіну қажеттігін ұғынады. Бұл тақырып жалпы білім беретін мектептерге арналған бағдарламада кірістірілмегендіктен, алдымызға келесідей мақсаттарды қойдық:

1. Санның бүтін және бөлшек бөлігі ұғымдарымен танысу;

2. $y = \lbrack x\rbrack, \ y = \left\{ x \right\}; y = (x), \ y = \left\{ \left\{ x \right\} \right\}$ және т. б. түрдегі функциялармен танысу;

3. Санның бүтін және бөлшек бөліктері функцияларының қасиеттерін қарастыру;

4. Санның бүтін және бөлшек бөліктері бар теңдеу мен теңсіздіктерді шешуді үйрену.

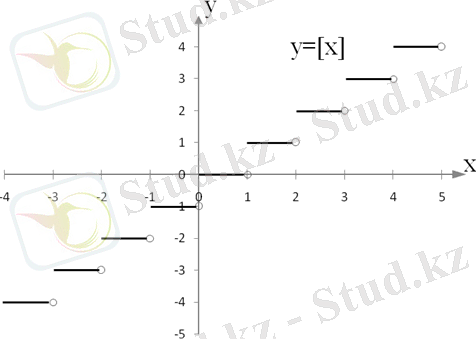
Анықтама. Берілген санының бүтін бөлігі (немесе антье) деп - сол саннан аспайтын ең үлкен бүтін санды айтамыз. $x$ санының бүтін бөлігі $\lbrack x\rbrack$ таңбасымен белгіленеді .

Анықтама. $x$ санының бүтін бөлігі деп, $\lbrack x\rbrack = c, \ c \leq x < c + 1$ болғандағы $x -$ тен аспайтын ең үлкен бүтін $c$ санын айтады.

Мысалы, $\lbrack 5\rbrack = 5$ ; $\lbrack - 6\rbrack = - 6$ ; $\lbrack 0\rbrack = 0$ ; $\lbrack 1, 7\rbrack = 1$ ; $\lbrack 7, 2\rbrack = 7$ ; $\lbrack - 1, 8\rbrack = - 2$ ; $\lbrack - 2, 3\rbrack = - 3$ ; $\lbrack - 7, 9\rbrack = - 8$ ; $\left\lbrack \frac{88}{9} \right\rbrack = 9$ ; $\left\lbrack \frac{11}{16} \right\rbrack = 0$ ; $\left\lbrack \sqrt{5} \right\rbrack = 2$ ; $\lbrack\pi\rbrack = 3$ .

Функцияның кейбір мәндері бойынша оның графигін тұрғызуға болады. $x$ санының бүтін бөлігінің графигі 1-суретте көрсетілген.

$y = \lbrack x\rbrack$ функциясының қасиеттеріне тоқталайық.

1. Анықталу облысы. Функцияның $x$ айнымалысының барлық мәндері үшін мағынасы бар, бұл санның бүтін бөлігін және сандық жиындардың қасиеттерін анықтаудан тұрады. Демек, оның анықталу облысы-барлық нақты сандар жиыны: $D(\lbrack x\rbrack) = R.$

2. Мәндер облысы. $y = \lbrack x\rbrack$ функциясының мәндерінің жиыны, бұл барлық бүтін сандардың жиыны (санның бүтін бөлігін анықтау бойынша) . $E(\lbrack x\rbrack) = Z$

3. Функцияның жұп немесе тақ екендігін анықтау. Жұп шарты да $f( - x) = f(x)$ , тақ шарты да $f( - x) = - f(x$ ) орындалмағандықтан, функция жалпы түрдегі функция болады.

1-сурет

4. Периодтылығы. $y = \lbrack x\rbrack$ функциясы периодтық емес.

5. Шектеулілігі. Функция шектелмеген, өйткені функцияның мәндер жиыны-барлық бүтін сандар жиыны. Бүтін сандар жиыны шектелмеген.

6. Үздіксіздігі. Үзілісті функция. $y$ -тің секіру қадамы $1$ -ге тең.

7. Функцияның нөлдері. $x$ аргументі $\lbrack 0; 1)$ аралығына тиісті болғанда, функцияның мәні $0$ -ге тең болады. Демек, функцияның нөлі осы аралықтың барлық мәндері болады.

8. Монотондық аралығы. Санның бүтін бөлігінің қасиеттерін ескере отырып, $y\ = \ \lbrack x\rbrack$ функциясы $x$ кіші нөлде теріс мәндерді қабылдайды, және $x$ $1$ -ден үлкен болғанда оң мәндерді қабылдайды.

9. Монотондық аралығы. $y = \lbrack x\rbrack$ функциясы бөлікті-тұрақты.

10. Экстремум нүктелері. Функцияның экстремум нүктелері жоқ, өйткені монотондылық сипатын өзгертпейді.

11. Функцияның ең үлкен және ең кіші мәндері. $y = \lbrack x\rbrack$ функциясы $\lbrack n\ ; \ n + 1)$ аралығында тұрақты болғандықтан, ол анықтау облысында ең үлкен және ең кіші мәндерді қабылдамайды. Ең үлкен және ең кіші мәндері жоқ.

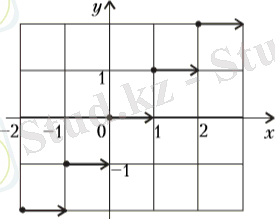
$y = \left\lfloor x \right\rfloor$ функция графигінің «табаны»

Әдебиеттерде ( $x$ санының «табаны») термині және оның белгіленуі $y = \left\lfloor x \right\rfloor$ кездеседі. Бұл да санның бүтін бөлігіне ұқсас. Демек, графигі $y = \lbrack x\rbrack$ функциясының графигімен толық сәйкес келеді.

$y = \left\lceil x \right\rceil$ функция графигінің «төбесі». $x$ санының «табанына» ұқсас $x$ санының «төбесі» функциясы анықталады және ол былай белгіленеді $y = \left\lceil x \right\rceil$ . Бұл $x$ -тен кем емес, ең кіші бүтін сан.

2-сурет

Мысалы, $\left\lceil - 2 \right\rceil = - 2, \ \left\lceil - \frac{1}{3} \right\rceil = 0, \ \left\lceil \pi \right\rceil = 4$ .

$y = \left\lceil x \right\rceil$ функциясының графигі оңнан солға, жоғарыдан төменге қарай жүретін және $AB = \ ( - 1, - 1)$ векторына параллельді тасымалда өзіне ауыспалы баспалдақтардан тұрады.

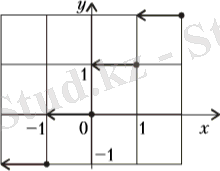
3-сурет

$y = (x)$ функциясы

$x$ бүтін санына жақын $y = (x)$ функциясы бар. Егер $x$ -ке жақын бүтін сан екеу ( $x = \frac{2k + 1}{2}$ , $x$ - бүтін сан) болса, онда олардың ең үлкенін таңдаймыз. Мысалға $(4, 53) = 5, \ (1, 5) = 2, \ ( - 2, 1) = - 2$ .

Санның бүтін бөлігін қамтитын функциялар графиктерін түрлендіру

$y = \left\lbrack f(x) \right\rbrack$ түріндегі функция графигін салу.

$y = f(х)$ функциясының графигі бар болсын. $y = \left\lbrack f(x) \right\rbrack$ функциясының графигін салу келесідей:

y=n, n=0; −1; +1; −2; +2; …y = n, \ n = 0; \ - 1; \ + 1; \ - 2; \ + 2; \ldots\түзулерін жүргізіп, y=n, y=n+1y = n, \ y = n + 1түзулерімен жүргізілген жолақтардың бірін қарастырамыз.
y=n, y=n+1y = n, \ y = n + 1түзулерініңy=f(x) y = f(x) функциясының графигімен жүргізілген қиылысу нүктелерін белгілейміз. Бұл нүктелерy=[f(x) ] y = \left\lbrack f(x) \right\rbrackфункциясының графигіне тиесілі, себебі олардың ординаттары бүтін сандар (олар суреттегіA, B, C, DA, \ B, \ C, \ Dнүктелері) .

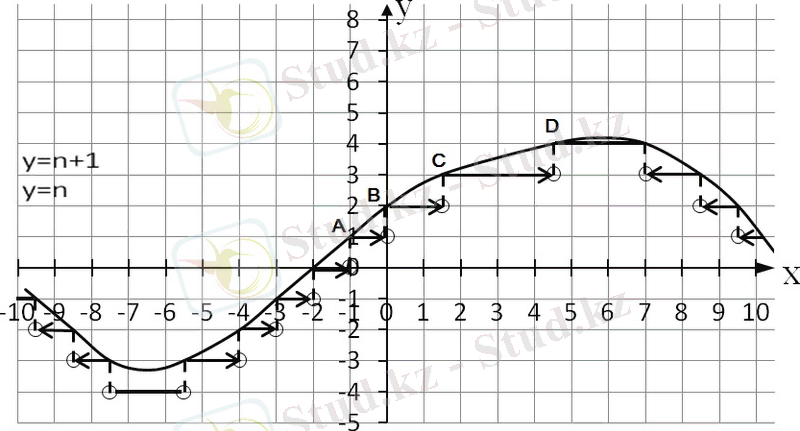
4-сурет

Берілген жолақтағыy=[f(x) ] y = \left\lbrack f(x) \right\rbrackфункциясының графигінің қалған нүктелерін алу үшін, жолаққа түскенy=f(x) y = f(x) графигінің бөлігінOyOyосіне параллельy=ny = nтүзуіне сызамыз. Сондықтан, y=f(x) y = f(x) функция графигінің кез келгенMMнүктесіn≤y0<n+1, y0n \leq y_{0} < n + 1, \ y_{0}ординаттарына ие болcа, онда[y0] =n\left\lbrack y_{0} \right\rbrack = n.
y=f(x) y = f(x) функциясының графигінің нүктелері бар басқа да жолаққа сызу ұқсас жүргізіледі.

$y = f\left( \lbrack x\rbrack \right)$ түріндегі функция графигін салу.

$y = f(x)$ функциясының графигі берілсін. $y = f\left( \lbrack x\rbrack \right)$ функциясының графигін салу былайша жүзеге асырылады:

x=n, n=0; −1; +1; −2; +2; …x = n, \ n = 0; \ - 1; \ + 1; \ - 2; \ + 2; \ldotsтүзулерін жүргіземіз.
y=ny = nжәнеy=n+1y = n + 1түзулері арқылы пайда болған жолақтардың бірін қарастырайық. y=f(x) y = f(x) функция нүктелеріy=f([x] ) y = f\left( \lbrack x\rbrack \right) функцияcының графигіне жатады, себебі олардың абсциссалары-бүтін сандар.

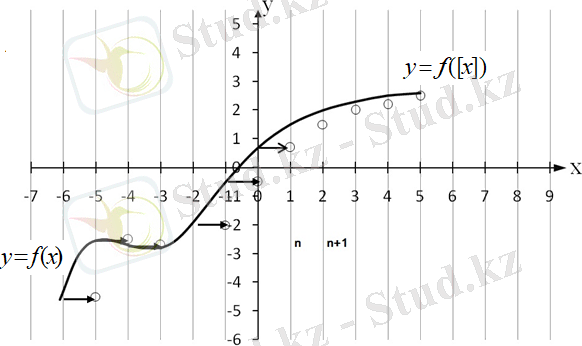
5-сурет

$y = \lbrack x\rbrack^{2}$ функцияcының графигін құруды қарастырайық. Ол үшін $y = x^{2}$ функциясының графигін құрайық . Одан әрі

1. $x = n, \ n = 0; \ - 1; \ + 1; \ - 2; \ + 2; \ldots$ түзулерін жүргіземіз.

2. $y = n$ және $y = n + 1$ түзулері арқылы пайда болған жолақтардың бірін қарастырайық. $y = x^{2}$ функция графигінің қиылысу нүктелері $y = \lbrack x\rbrack^{2}$ функцияcының графигіне жатады, себебі олардың абсциссалары-бүтін сандар.

y=x2y = x^{2}функциясының графигінің нүктелері бар басқа да жолаққа сызу ұқсас жүргізіледі.

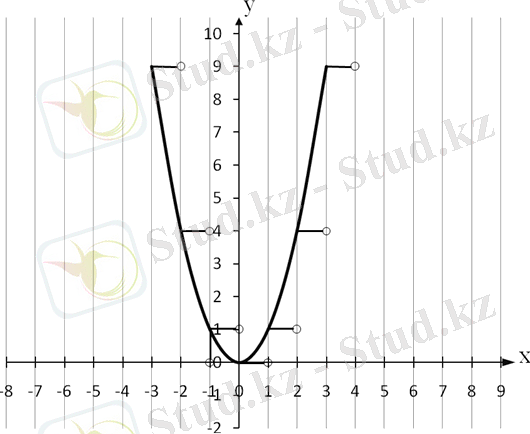
6-сурет

Санның бүтін бөлігіне берілген қарапайым теңдеулерді қарастырайық

Қарапайым теңдеулерге $\lbrack x\rbrack = a$ түріндегі теңдеулер жатады. Мұндай түрдегі теңдеулер анықтама бойынша шешіледі.

$a \leq x < a + 1$ , мұндағы $a -$ бүтін сан. Егер $a -$ бөлшек сан болса, онда мұндай теңдеудің түбірі болмайды.

Осындай теңдеулердің бірінің шешу мысалын қарастырайық.

Мысал 1. $\lbrack x + 1, 3\rbrack = - 5$ теңдеуін шешіңіз.

Шешуі: Анықтама бойынша $\lbrack x + 1, 3\rbrack = - 5$ теңдеу мынадай $- 5 \leq x + 1, 3\ < - \ 4$ теңсіздігіне түрленеді $.$ Оны шешсек, $- 6, 3 \leq x < - \ 5, 3$ аламыз. Бұл теңдеудің шешімі болады.

Жауабы: $x \in \lbrack - 6, 3; \ - 5, 3)$

Мысал 2. $\lbrack x + 1\rbrack + \lbrack x - 2\rbrack - \lbrack x + 3\rbrack = 2$ теңдеуін шешіңіз.

Шешуі: Мұндай түрдегі теңдеулерді шешу үшін бүтін сан функциясының қасиетін пайдалану қажет. Егер $p -$ бүтін сан болса, онда $\lbrack x \pm p\rbrack = \lbrack x\rbrack \pm p$ болады.