Операциялық есептеу әдістерін дифференциалдық теңдеулерді шешуде қолдану


Қазақстан Республикасының Білім және ғылым министрлігі
Л. Н. Гумилев атындағы Еуразия ұлттық университеті
Операциялық есептеуді дифференциалдық теңдеулерді шешуге қолдану
ДИПЛОМДЫҚ ЖҰМЫС
5В060100 - «Математика» мамандығы
Нұр-Сұлтан 2019
Қазақстан Республикасының Білім және ғылым министрлігі
Л. Н. Гумилев атындағы Еуразия ұлттық университеті
«Қорғауға жіберілді»
Іргелі математика
кафедрасының меңгерушісі м. а.
М. Алдай
ДИПЛОМДЫҚ ЖҰМЫС
Тақырыбы: «Операциялық есептеуді дифференциалдық теңдеулерді шешуге қолдану»
5B060100- «Математика» мамандығы бойынша
Орындаған: Жорабек Меруерт Аманқызы
Ғылыми жетекші: Мырзатаева Калбиби Раевна
Ф-м. ғ. кандидаты, доцент
Нұр-Сұлтан 2019
Л. Н. Гумилев атындағы Еуразия ұлттық университеті
Л. Н. Гумилев атынтағы Еуразия ұлттық университеті
Механика - математика факультеті
5B060100 - «Математика» мамандығы
Іргелі математика кафедрасы
«Бекітемін»
Іргелі математика
кафедра меңгерушісі м. а.,
Алдай М.
«___» 2019 ж.
Дипломдық жұмысты орындауға арналған
ТАПСЫРМА
Студент Жорабек Меруерт Аманқызы
4курс, М 41тобы, 5B060100 - «Математика» мамандығы, күндізгі
- Дипломдық жұмыстың тақырыбы: «Операциялық есептеуді дифференциалдық теңдеулерді шешуге қолдану»2018ж. «21» желтоқсанайында №1587-П ректордың бұйрығымен бекітілген.
- Студенттің аяқталған жұмысты тапсыру мерзімі«17» сәуір2019ж.
- Жұмыстың бастапқы деректері: Дипломдық жұмыстың тақырыбына байланысты ғылыми әдебиеттерге шолу жасалады.
- Дипломдық жұмыста қарастырылатын сұрақтардың тізбегі:
a)
ә)
- Графикалық материалдардың тізбегі (сызбалар, кестелер т. с. с) .
- Негізгі ұсынылған әдебиеттер тізімі:
a)
ә)
- Жұмыс бойынша берілген кестелер (тиісті бөлімдері көрсетілген)
8. Дипломдық жұмысты орындау кестесі:
9. Тапсырманың берілген уақыты « » 2018 ж.
Ғылыми жетекшісі: Мырзатаева К. Р.
Тапсырманы қабылдаған: Жорабек М. А.
МАЗМҰНЫ
1. 2 Лаплас түрлендіруі және оның қасиеттері. Функцияның бейнесі
1. 3 Бейне бойынша түпнұсқаны табу
1. 4 Дюамель формуласы
11
18
23
КІРІСПЕ
Операциялық есептеу математикалық анлиздің маңызды бір саласы болып табылады. Механика, математика және техника есептерін шешуде операциялық есептеу әдістері жиі қолданылады. Жылу өткізгіштік теориясында, электротехника және радиотехника, электр тізбегіндегі тұрақты емес құбылыстарды, автоматты реттегіштер жүйесінің жұмысын зерттеуде, сонымен қатар сызықты дифференциалдық және интегралдық, айырымдық теңдеулер теориясында операциялық есептеу әдістері кеңінен қолданылады.
Оператор, операция сөздері латын тілінен аударғанда operor-жасаймын, operator-жасаушы, жұмыскер деген ұғымды білдіреді. Ал operatio-амал, қимыл, жұмыс, енгізу, іске асыру ұғымдарына сәйкес келеді. Операциялық есептеу саласындағы алғашқы ғылыми жұмыстар белгілерді есептеу, белгілеулер енгізу арқылы есептеу деген сияқты атаулармен басталады. Операциялық әдістерді физикалық және техникалық есептерді шешу үшін қолдану ағылшын ғалымы Хевисайдтың 1892 жылы жарияланған еңбектерінен кейін басталған.Операциялық есептеудің алғашқы математикалық түрде негізді дәлелденуі ағылшын математигі Бромвичтің (1916), америкалық инженер Карсонның (1926) және Голландияның инженер-электригі Ван дер Польдің (1929-1932) еңбектерімен тығыз байланысты. Россияда бұл саладағы алғашқы еңбектердің бірі М. Е. Ващенко-Захарченконың 1862 жылы шыққан монографиясы болып табылады. Бұл монографияда символикалық есептеулердің мазмұны толық ашылып көрсетілген, сонымен қатар, сызықты дифференциалдық коэффициенттері тұрақты және айнымалы дифференциалдық теңдеулердің шешімін табуға қалай қолдану керектігі көрсетілген. Сонымен қатар операциялық есептеулердің ең негізгі формуласы беріліп, ол қазіргі уақытта есептің шешімін табудың негізгі класын кеңейтуге мүмкіндік береді. Операциялық есептеу теориясын дамытуға орыс ғалымдары Лурье А. И., Данилевский А. Н., Эфрос А. М., Конторович М. И., Диткин В. А. айтарлықтай үлес қосты.
Ғылыми зерттеулер нәтижесінде операциялық есептеу теориясында Лаплас бойынша түрлендірілетін функцияларды ғана пайдалану, оның қолданылу өрісін тарылтатындығы байқалды. Бұл кемшіліктен құтылу үшін Хевисайдтың белгілеулеріне қайта оралып, функция ұғымын жалпылау қажеттілігі туды. Осындай қажеттілікпен байланысты жарыққа шыққан польша математигі Я. Микусинскийдің «Операциялық есептеу» деп аталатын еңбегі алғашқы операциялық көзқарасқа қайта оралудың бастамасы болды.
Дипломдық жұмыстың мақсаты. Коэффициенттері тұрақты және айнымалы бірінші ретті сызықты дифференциалдық теңдеулер және теңдеулер жүйесінің шешімін табуда операциялық есептеулерді, атап айтқанда Лаплас түрлендіруін қолдану болып табылады. Операциялық есептеулерлің ерекшеліктерін зерттеу.
Дипломдық жұмыстың міндеттері:
1 Жай дифференциалдық теңдеулерді шешуді операторлық теңдеуді шешуге айналдыру;
2 Лаплас түрлендіруінің ерекшеліктерін зерттеу;
3 Басқа да интералдық түрлендірудің дифференциалдық теңдеулерді шешуде қолдануларын қарастыру;
Зерттеу нысаны. Зерттеудің негізгі нысаны болып дифференциалдық теңдеулерге операциялық есептеулерді пайдаланып, берілген теңдеудің шешімін табу болып табылады.
Зерттеу пәні. Зерттеудің негізгі пәні операциялық есептеулер мен дифференциалдық теңдеулер болып табылады.
Дипломдық жұмыстың жаңашылдығы. Жұмыста біртекті емес оң жағы рационал көпмүшелік, үзілісті және үзіліссіз функциялар болғандағы коэффициенттері тұрақты сызықты дифференциалдық теңдеудің шешімін операциялық есептеулер көмегімен, атап айтқанда, Лаплас түрлендіруін пайдаланып табу қарастырылған. Дюамель интегралын пайдалана отырып сызықты дифференциалдық теңдеуді шешу қарастырылған. Сонымен қатар Фурье, Меллин, Ханкель түрлендірулерін пайдаланып, дербес туындыдағы теңдеулерді шешімі анықталған.
Дипломдық жұмыстың құрылымы. Дипломдық жұмыс кіріспе, негізгі бөлім, қортынды, пайдаланылған әдебиеттер тізімі мен қосымшадан тұрады. Кіріспеде алдыңғы ғылыми жұмыстарға қысқаша шолу жасалынған және осы диломық жұмыстың тақырыбының маңыздылығы, мақсаты, зерттеу міндеттері мен нәтижелерінен шыққан жаңалықтар келтірілген. Дипломдық жұмыстың қысқаша баяндалу мазмұны келтірілген.
Дипломдық жұмыстың негізгі бөлімі 3 тараудан тұрады. 1-тарау теориялық сипаттамадан тұрады. Операциялық есептеудің негізі болып саналатын Лаплас түрлендіруінің анықтамасы мен оның қасиеттеріне тоқталап отырып, түпнұсқадан бейнеге және керісінше бейне бойынша түпнұсқаны табу әдістерін қарастырдым. Дюамель формуласына қысқаша анықтама бірілді.
Дипломдық жұмыстың 2-тарауында Лаплас түрлендіруінің дифференциалдық теңдеулерді шешуде қолдануын қарастырдым. Атап айтқанда, коэффициенттері тұрақты сызықтық дифференциалдық теңдеулерді операциялық әдіспен шешуді, сызықтық дифференциалдық теңдеулерді Дюамель интегралын пайдалана отырып, шығаруды және коэффициенттері тұрақты сызықтық дифференциалдық теңдеулердің жүйесін операциялық әдіс арқылы шешуді қарастырдым.
Негізгі бөлімінің соңғы тарауында Лаплас түрлендіруінен басқа да интегралдық түрлендірулер бар екендігін және Лаплас түрлендіруі тек дербес жағдайы екендігін ескере отырып, Фурье, Меллин және Ханкель түрлендірулеріне қысқаша анықтама беріп, олардың кейдір қолданулары қарастырыладым.
1 ОПЕРАЦИЯЛЫҚ ЕСЕПТЕУ
1. 1 Түпнұсқаның қасиеттері
Операциялық есептеу Лаплас түрлендіруінің қасиеттері мен оның көмегімен әр түрлі есептерді шешуді қарастыратын математикалық анализдің бір бөлігі.
Лаплас түрлендіруі функцияларды сәйкес қою заңдылығын анықтайды, яғни қандай да бір жиындағы кез келген бір айнымалыдан тәуелді функцияны сол жиындағы бір айнымалыдан тәуелді басқа бір функцияға сәйкес қоятын заңдылық. Функциялар жиынындағы бұндай сәйкестікті оператор деп атайды.
1- анықтама
Нақты
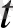 айнымалыдан тәуелді кез келген
айнымалыдан тәуелді кез келген
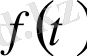 функцияны түпнұсқа деп атайы, егер бұл функция төмендегі шарттарды қанағаттандырса:
функцияны түпнұсқа деп атайы, егер бұл функция төмендегі шарттарды қанағаттандырса:
1
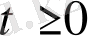 мәндерінде
мәндерінде
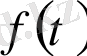 бөлік-бөлік үзіліссіз, яғни
бөлік-бөлік үзіліссіз, яғни
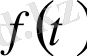 - үзіліссіз болады немесе кез келген ақырлы интервалда санаулы бірінші түрдегі үзіліс нүктелері бар.
- үзіліссіз болады немесе кез келген ақырлы интервалда санаулы бірінші түрдегі үзіліс нүктелері бар.
2
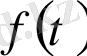
 , егер
, егер
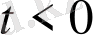 , болса;
, болса;
3
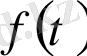
 кейбір көрсеткіштік функциядан тез өспейді, яғни
кейбір көрсеткіштік функциядан тез өспейді, яғни
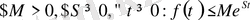 (1. 1) теңсіздігі орындалса (шенелген өсу аралығы болады) ;
(1. 1) теңсіздігі орындалса (шенелген өсу аралығы болады) ;
2- анықтама
(1) теңсіздік орындалатын
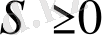 сандардың ең кішісі
сандардың ең кішісі
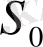 -
-
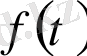 функциясының өсу көрсеткіші деп аталады. [1, 221-222 б. б]
функциясының өсу көрсеткіші деп аталады. [1, 221-222 б. б]
Ескерту 1
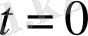 нүктесі
нүктесі
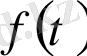 түпнұсқасының бірінші түрдегі үзіліс нүктесі болса, онда
түпнұсқасының бірінші түрдегі үзіліс нүктесі болса, онда
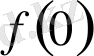 ретінде
ретінде
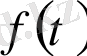 функциясының шегін қарастырамыз, яғни
функциясының шегін қарастырамыз, яғни
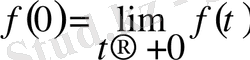 .
.
Ескерту 2
(1) теңсіздік кез келген шенелген функция үшін орындалады, дербес жағдайда
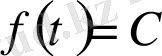 ,
,
 функциясы үшін де орындалады. Бұл функция үшін
функциясы үшін де орындалады. Бұл функция үшін
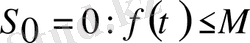 .
.
(1) теңсіздікті барлық дәрежелік функциялар да қанағаттандырады.
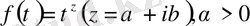 бұл функцияның модулі көрсеткіштік функция
бұл функцияның модулі көрсеткіштік функция
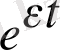
қарағанда жай өседі.
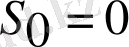 ;
;
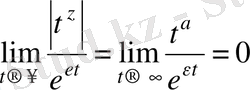
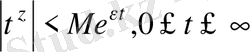 .
.
Егер
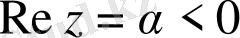 болса, онда
болса, онда
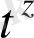 функцисы
функцисы
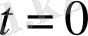 нүктесінде ақырсыз үзіле береді. Сондықтан (1) теңсіздік орындалмайды, функция түпнұсқа емес.
нүктесінде ақырсыз үзіле береді. Сондықтан (1) теңсіздік орындалмайды, функция түпнұсқа емес.
Ескерту 3
Көптеген физикалық процестерді қарастырған кезде
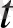 айнымалысы уақыт, жол, жылдамдықты анықтайды. Сондықтан анықтамадағы 2-шарт практикада маңызды емес. Алдағы уақытта белгілі бір түпнұсқа функция қарастырсақ, нақтырақ айтсақ
айнымалысы уақыт, жол, жылдамдықты анықтайды. Сондықтан анықтамадағы 2-шарт практикада маңызды емес. Алдағы уақытта белгілі бір түпнұсқа функция қарастырсақ, нақтырақ айтсақ
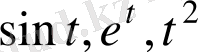 , т. с. с функциялар қарастыратын болсақ
, т. с. с функциялар қарастыратын болсақ
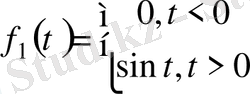 ,
,
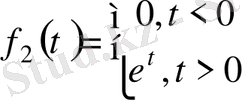 осындай функциялар деп есептейміз. егер
осындай функциялар деп есептейміз. егер
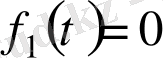 болса, онда
болса, онда
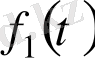 функциясы
функциясы
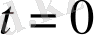 нүктесінде үзіліссіз.
нүктесінде үзіліссіз.
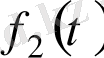 функциясы
функциясы
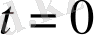 нүктесінде бірінші түрдегі үзіліс нүктесі болады. Қысқаша
нүктесінде бірінші түрдегі үзіліс нүктесі болады. Қысқаша
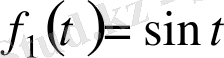 ,
,
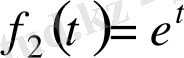 түрінде жазамыз.
түрінде жазамыз.
Түпнұсқаның қасиеттері
1. Егер
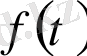 түпнұсқа болса, онда
түпнұсқа болса, онда
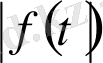 функциясы да түпнұсқа болады және осы екі функцияның өсу көрсеткіштері бірдей болады.
функциясы да түпнұсқа болады және осы екі функцияның өсу көрсеткіштері бірдей болады.
2. Егер
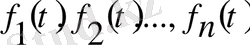 түпнұсқа функцияларының өсу көрсеткіштері
түпнұсқа функцияларының өсу көрсеткіштері
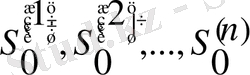 өсу көрсеткіштері болса, онда
өсу көрсеткіштері болса, онда
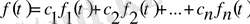 , мұндағы
, мұндағы
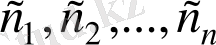 -тұрақтылар (нақты немесе комплекс сан) фунциясы да түпнұсқа болады және оның өсу көрсеткіші
-тұрақтылар (нақты немесе комплекс сан) фунциясы да түпнұсқа болады және оның өсу көрсеткіші
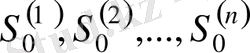 -дердің ең үлкеніне тең болады.
-дердің ең үлкеніне тең болады.
3.
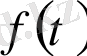 түпнұсқа функциясының өсу көрсеткіші
түпнұсқа функциясының өсу көрсеткіші
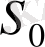 болса, онда келесі функциялар түпнұсқа болады:
болса, онда келесі функциялар түпнұсқа болады:
a)
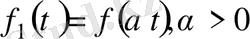 және өсу көрсеткіші
және өсу көрсеткіші
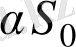
ә)
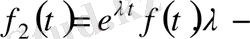 нақты немесе комплекс сан, функциясының өсу
нақты немесе комплекс сан, функциясының өсу
көрсеткіші
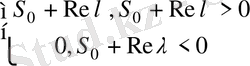 тең болады.
тең болады.
б)
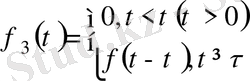 функциясының өсу көрсеткіші
функциясының өсу көрсеткіші
 .
.
в)
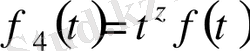 (z-нақты немесе комплекс сан) өсу көрсеткіші
(z-нақты немесе комплекс сан) өсу көрсеткіші
 .
.
4. Егер
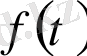 түпнұсқа және өсу көрсеткіші
түпнұсқа және өсу көрсеткіші
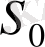 болса, онда
болса, онда
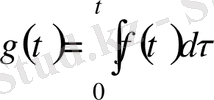
функциясы
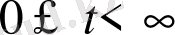 интервалында үзіліссіз түпнұсқа және өсу көрсеткіші
интервалында үзіліссіз түпнұсқа және өсу көрсеткіші
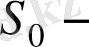 ге тең болады. [2, 4-6 б. б. ]
ге тең болады. [2, 4-6 б. б. ]
1. 2. Лаплас түрлендіруі және оның қасиеттері. Функцияның бейнесі
3- анықтама
Нақты
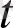 айнымалы
айнымалы
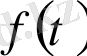 түпнұсқа функциясының Лаплас түрлендіруі деп,
түпнұсқа функциясының Лаплас түрлендіруі деп,
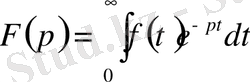 (1. 2)
(1. 2)
формуласымен анықталaтын комплекс айнымалы
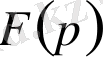 функциясын айтады. Теңдіктің оң жағындағы комплекс
функциясын айтады. Теңдіктің оң жағындағы комплекс
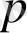 -ға тəуелді меншіксіз интеграл Лаплас интегралы деп аталады. [3, 254 б. ]
-ға тəуелді меншіксіз интеграл Лаплас интегралы деп аталады. [3, 254 б. ]
1- теорема
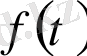 түпнұсқа функциясының өсу көрсеткіші
түпнұсқа функциясының өсу көрсеткіші
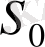 болсын. Онда (2) интегралы
болсын. Онда (2) интегралы
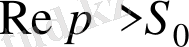 шартын қанағаттандыратын
шартын қанағаттандыратын
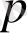 комплекс айнымалысының кез келген мәнінде жинақталатын сонымен қатар кез келген
комплекс айнымалысының кез келген мәнінде жинақталатын сонымен қатар кез келген
 нүктесінде
нүктесінде
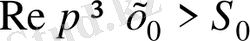 шарты орындалған кезде бірқалыпты жинақталатын және
шарты орындалған кезде бірқалыпты жинақталатын және
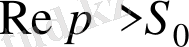 жартылай жазықтықта аналитикалық функция болатын
жартылай жазықтықта аналитикалық функция болатын
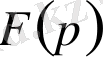 функциясын анықтайды. [1, 222-225 б. б. ]
функциясын анықтайды. [1, 222-225 б. б. ]
4- анықтама
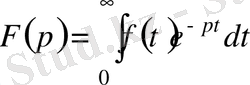 функциясы
функциясы
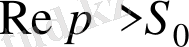 жартылай жазықтықта
жартылай жазықтықта
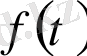 функциясының Лаплас бойынша бейнесі деп аталады.
функциясының Лаплас бойынша бейнесі деп аталады.
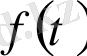 мен
мен
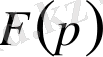 арасындағы байланыс (1. 2) формуласымен
арасындағы байланыс (1. 2) формуласымен
анықталады және алдағы уақытта
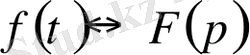 деп белгілейтін боламыз.
деп белгілейтін боламыз.
Мысал 1 Мысал ретінде бірлік функцияны (бірлік Хевисайда функциясын) қарастырамыз және оның бейнесін табамыз. [4, 388-389 б. б. ]
Шешуі: бірлік функция келесідей болады:
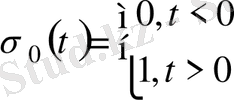 және графигі 1-суретте бейнеленген.
және графигі 1-суретте бейнеленген.
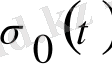
1-сурет Бірлік функцияның графигі
Бірлік фунуция түпнұсқа болады. Оның бейнесін табайық. 3- анықтама бойынша
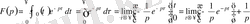
Осыдан бейненің бар болуы үшін ақырлы шек бар болатындығын көрсетеміз.
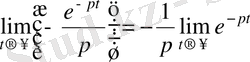
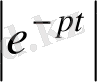 -ны қарастырайық.
-ны қарастырайық.
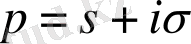 екендігін пайдаланып,
екендігін пайдаланып,
 аламыз. Мұнда біз Эйлер формуласын және комплекс санның модулін комплекс санның модулін табу анықтамасын қолдандық. Әрі қарай 2 жағдай қарастырамыз.
аламыз. Мұнда біз Эйлер формуласын және комплекс санның модулін комплекс санның модулін табу анықтамасын қолдандық. Әрі қарай 2 жағдай қарастырамыз.
1.
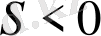 болсын, онда
болсын, онда
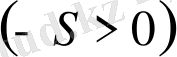 :
:
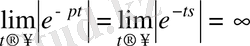
2.
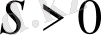 болсын, онда
болсын, онда
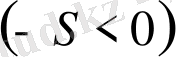 :
:
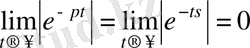
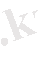
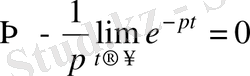
Жоғарыдағы талқылаулардан кейін келесідей қортынды жасауға болады. Бірлік функцияның бейнесі тек
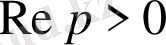 , яғни
, яғни
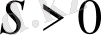 болған жағдайда ғана бар болады. Сонымен
болған жағдайда ғана бар болады. Сонымен
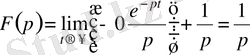
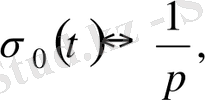 егер
егер
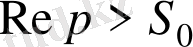
Мысал 2
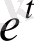 көрсеткіштік функциясының бейнесін табайық.
көрсеткіштік функциясының бейнесін табайық.
Шешуі:
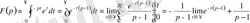
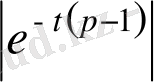 -ді қарастырайық.
-ді қарастырайық.
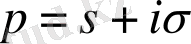 екендігін пайдалансақ,
екендігін пайдалансақ,
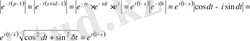
2 жағдай қарастырамыз.
1. Егер
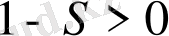 болса,
болса,
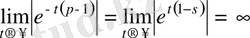
2. Егер
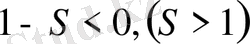 болса,
болса,
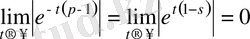
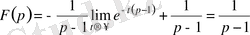 , егер
, егер
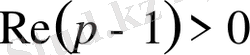 , яғни
, яғни
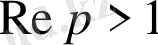
Онда
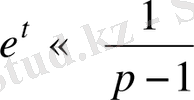 , егер
, егер
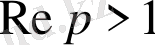 болса.
болса.
Лаплас түрлендіруінің қасиеттері
Лаплас түрлендіруінің негзгі қасиеттері мен ережелеріне (немесе операциялық есептеудің негзгі қасиеттері мен ережелері) байланысты теоремаларды қарастыратын боламыз. Осы қасиеттерге сүйеніп, түпнұсқа мен бейненің арасындағы байланыс кестесін пайдалана отырып, түпнұсқадан бейнеге, және керісінше бейнеден түпнұсқаға өтеміз.
Түпнұсқа функцияларды
 және т. с. с және сәйкесінше бейнені
және т. с. с және сәйкесінше бейнені
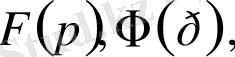 т. с. с белгілейтін боламыз.
т. с. с белгілейтін боламыз.
Жалғыздық теоремасы.
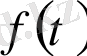 түпнұсқасы толығымен өзінің
түпнұсқасы толығымен өзінің
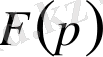 бейнесімен анықталады, мұндағы дәлдік
бейнесімен анықталады, мұндағы дәлдік
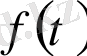 функциясының үзіліс нүктелеріне дейін. Басқаша айтсақ, егер 2 бейне
функциясының үзіліс нүктелеріне дейін. Басқаша айтсақ, егер 2 бейне
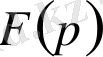 және
және
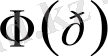 тең болса онда сәйкесінше үзіліс нүктелерінен басқа кез келген нүктеде олардың түпнұсқалары да тең өзара тең болады, яғни егер
тең болса онда сәйкесінше үзіліс нүктелерінен басқа кез келген нүктеде олардың түпнұсқалары да тең өзара тең болады, яғни егер
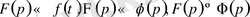 онда
онда
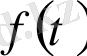 -ның кез келген үзіліссіз нүктелерінде
-ның кез келген үзіліссіз нүктелерінде
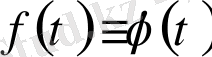 теңдігі орындалады. [5]
теңдігі орындалады. [5]
Теоремадан
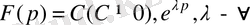

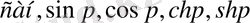 функциялары бейне бола алмайды.
функциялары бейне бола алмайды.
Сызықтық теоремасы. Егер
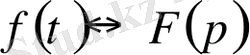 ,
,
 және
және
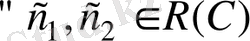
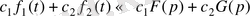
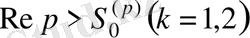 , яғни түпнұсқалардың сызықты комбинациясы бейнелердің сызықты комбинациясына сәйкес келеді.
, яғни түпнұсқалардың сызықты комбинациясы бейнелердің сызықты комбинациясына сәйкес келеді.
Теореманы кез келген ақырлы сан үшін де жалпылауға болады.
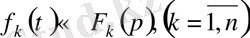 онда
онда
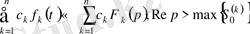 , мұндағы
, мұндағы
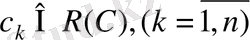
Мысал: а)
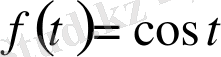
Эйлер формуласы бойынша:
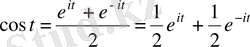
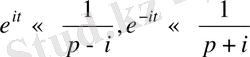 , сызықтық теоремасын қолданып,
, сызықтық теоремасын қолданып,
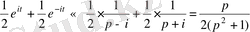
б)
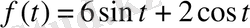
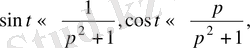 сызықтық теоремасын қолданып,
сызықтық теоремасын қолданып,
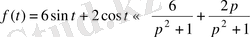
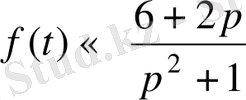
Ұқсастық теоремасы. Егер
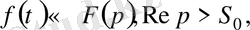 болса, онда
болса, онда
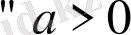 үшін
үшін
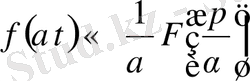 ,
,
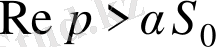 яғни түпнұсқаның аргументін оң санға көбейту оны бейнені сол санға бөлуге және бейненің аргументін
яғни түпнұсқаның аргументін оң санға көбейту оны бейнені сол санға бөлуге және бейненің аргументін
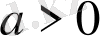 санына бөлуге әкелкеді. [6]
санына бөлуге әкелкеді. [6]
Расында да
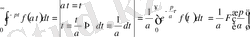
Мысал:
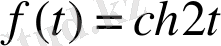
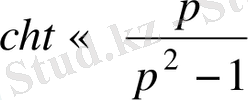
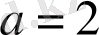 ұқсастық теоремасы бойынша
ұқсастық теоремасы бойынша
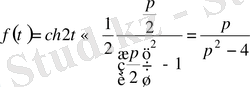
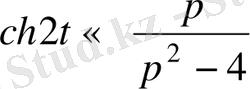
Кешігу теоремасы.
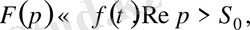 болсын, және
болсын, және
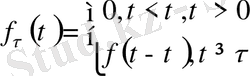 берілген болсын. Онда
берілген болсын. Онда
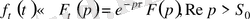 орындалады . [5]
орындалады . [5]
Мысал:
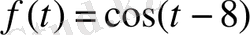
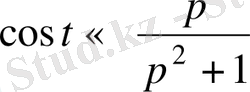 , онда кешігу теоремасы бойынша
, онда кешігу теоремасы бойынша
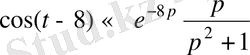 .
.
Ығысу теоремасы. Егер
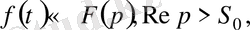 онда
онда
 саны үшін
саны үшін
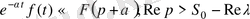 , яғни түпнұсқа
, яғни түпнұсқа
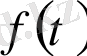 фунуциясының
фунуциясының
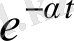 -ға көбейтіндісі
-ға көбейтіндісі
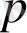 айнымалысының аустыруына әкеледі.
айнымалысының аустыруына әкеледі.
Расында да,
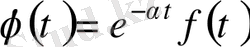 функциясы бейненің бар болу шарттарын қанағаттадырады. Енді формула бойынша
функциясы бейненің бар болу шарттарын қанағаттадырады. Енді формула бойынша

Теорема дәлелденді.
Мысал:
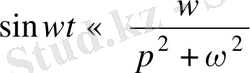
Онда
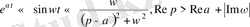 .
.
Шектеу теоремасы. Егер
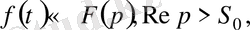 онда
онда
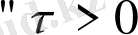 үшін
үшін
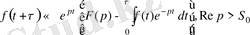 .
.
Параметр бойынша дифференциалдау теоремасы. Егер
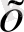 -тің кез келген мәнінде
-тің кез келген мәнінде
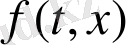 түпнұсқасына
түпнұсқасына
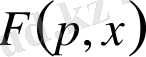 бейнесі сәйкес қойылса, онда
бейнесі сәйкес қойылса, онда
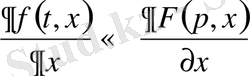 сәйкес қойылады.
сәйкес қойылады.
Мысал:
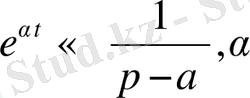 -параметр. Оң жағын да, сол жағын да
-параметр. Оң жағын да, сол жағын да

параметріне бойынша интегралдап:
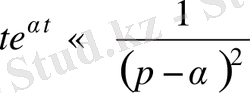
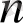 рет қайталап:
рет қайталап:
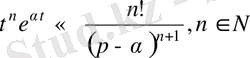
Түнұсқаны дифференциалдау теоремасы.
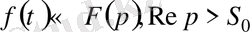 болсын. Егер
болсын. Егер
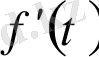 функциясы түпнұсқа болса, онда
функциясы түпнұсқа болса, онда
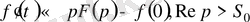 сәйкес қойылады. [7]
сәйкес қойылады. [7]
Расында да, бөліктеп интегралдау арқылы
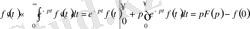 аламыз.
аламыз.
Егер
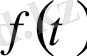 функциясы
функциясы
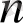 рет дифференциалданып, оның туындыларының барлығы түпнұсқа болатын болса, және
рет дифференциалданып, оның туындыларының барлығы түпнұсқа болатын болса, және
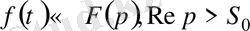 онда
онда
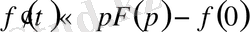
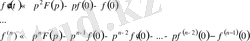
Бастапқы шарты 0-дік болған кезде түпнұсқаны
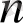 рет дифференциалдау оның бейнесін
рет дифференциалдау оның бейнесін
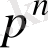 көбейтуге әкеледі.
көбейтуге әкеледі.
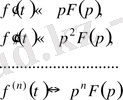
Түпнұсқаны интегралдау теоремасы.
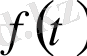 түпнұсқа функция берілсін және
түпнұсқа функция берілсін және
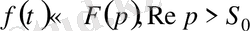 болсын, онда
болсын, онда
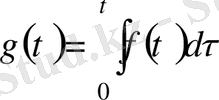 функциясы да түпнұсқа болады және
функциясы да түпнұсқа болады және
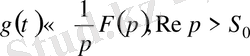 .
.
Расында да,
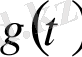 функциясы өсу көрсеткіші
функциясы өсу көрсеткіші
 болатын түпнұсқа болады. Енді
болатын түпнұсқа болады. Енді
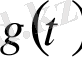 функциясының бейнесін табайық.
функциясының бейнесін табайық.
 осы соңғы интегралдан интегралдау ретін ауыстырамыз.
осы соңғы интегралдан интегралдау ретін ауыстырамыз.
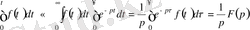
Жалпы жағдайы үшін
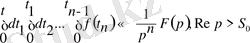 орындалады.
орындалады.
Мысал:
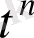 функциясының бейнесін табу керек.
функциясының бейнесін табу керек.
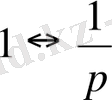 ,
,
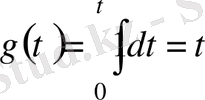
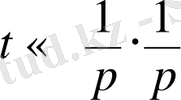 ,
,
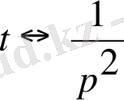
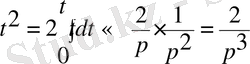
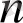 рет жалғастырып,
рет жалғастырып,
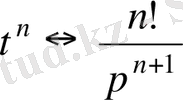 .
.
Бейнені дифференциалдау теоремасы. Егер
 , онда
, онда
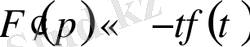 яғни бейнеден туынды алу түпнұсқаны
яғни бейнеден туынды алу түпнұсқаны
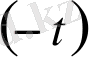 -ға көбейтіндісіне бейнелейді.
-ға көбейтіндісіне бейнелейді.
Расында да,
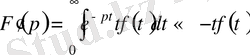
Егер
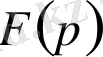 функциясы
функциясы
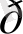 парметрі бойынша
парметрі бойынша
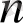 рет дифференциалданса, онда
рет дифференциалданса, онда
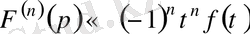
Бейнені интегралдау теоремасы. Егер
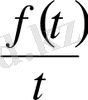 функциясы түпнұсқа болса
функциясы түпнұсқа болса
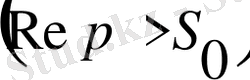 және
және
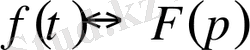 болса, онда
болса, онда
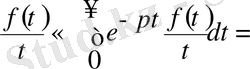
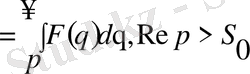 .
.
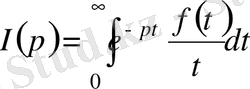 деп белгілеп алаайық. Бұл функция
деп белгілеп алаайық. Бұл функция
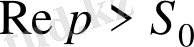 облысында аналитикалық функция болады және
облысында аналитикалық функция болады және
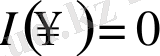 .
.
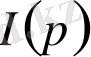 функциясынан туынды алайық. Интегралды
функциясынан туынды алайық. Интегралды
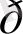 парметрі бойынша дифференциалдап,
парметрі бойынша дифференциалдап,
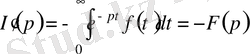
Осында
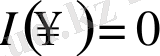 шартын ескеріп, келесіні аламыз:
шартын ескеріп, келесіні аламыз:
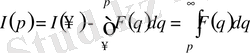 . Теорема дәлелденді.
. Теорема дәлелденді.
Бейнелердің қасиеттері 1-қосымшада кесте түрінде берілген
Негізгі түпнұсқалар мен олардың бейнелері 2-қосымшада көрсетілген.
1. 3 Бейне бойынша түпнұсқаны табу
Меллин формуласы. Берілген
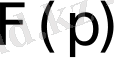 бейнесінен оған сәйкес
бейнесінен оған сәйкес
 түпнұсқасына көшу үшін Лапластың кері түрлендіруі орындалады.
түпнұсқасына көшу үшін Лапластың кері түрлендіруі орындалады.
Теорема. Түпнұсқа
 үзіліссіз нүктелерінде
үзіліссіз нүктелерінде
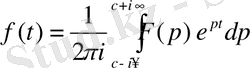 (1. 3)
(1. 3)
теңдігімен анықталады, мұндағы
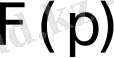 функциясы
функциясы
 түпнұсқасының Лаплас бойынша бейнесі. [8]
түпнұсқасының Лаплас бойынша бейнесі. [8]
Теңдіктің оң жағындағы интеграл бас мән мағынасындағы интегралды анықтайды. Басқаша айтқанда
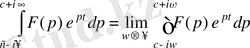
арақатынасы орындалады да, интеграл
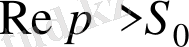 жарты жазықтығында жатқан және жорaмал оське параллель түзу бойынша алынады.
жарты жазықтығында жатқан және жорaмал оське параллель түзу бойынша алынады.
(1. 3) формуласы Мелиннің кері айналдыру формуласы деп аталады. Ол
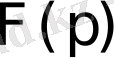 бейнесімен
бейнесімен
 түпнұсқасын байланыстырады.
түпнұсқасын байланыстырады.
Берілген
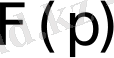 бейнесі бойынша түпнұсқаны табу Лапластың кері түрлендіруі болып табылады. Оны былай белгілейді:
бейнесі бойынша түпнұсқаны табу Лапластың кері түрлендіруі болып табылады. Оны былай белгілейді:
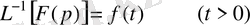
Мұндағы
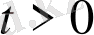 шарты
шарты
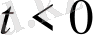 болғанда функцияның
болғанда функцияның
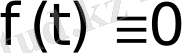 шартын қанағаттандыратынын көрсетеді.
шартын қанағаттандыратынын көрсетеді.
Мелиннің кері айналдыру формуласы бейнені тек үзіліссіз нүетелерінде ғана анықтайды. Бірақ
 түпнұсқасының бірінші текті үзіліс нүктелері болуы мүмкін.
түпнұсқасының бірінші текті үзіліс нүктелері болуы мүмкін.
Бұл жағдайда түпнұсқаның
 үзіліс нүетелерінде
үзіліс нүетелерінде

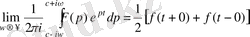
шарты орындалатындығын көрсетуге болады.
Сонымен, кері айналдыру формуласы
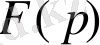 бейнесі бойынша
бейнесі бойынша
 түпнұсқасы оның үзіліс нүетелеріндегі мәндеріне дейінгі дәлдікпен анықталады. Түпнұсқаға бір ғана бейне сәйкес келеді. Себебі түпнұсқаның үзіліс нүетелеріндегі мәндері бейненің түрін өзгертпейді. Дегенмен де бір бейнеге бір-бірінен айырмашылығы үзілісн үетелеріндегі мәндерінде болатын түпнұсқалар жиынын сәйкес қоюға болады.
түпнұсқасы оның үзіліс нүетелеріндегі мәндеріне дейінгі дәлдікпен анықталады. Түпнұсқаға бір ғана бейне сәйкес келеді. Себебі түпнұсқаның үзіліс нүетелеріндегі мәндері бейненің түрін өзгертпейді. Дегенмен де бір бейнеге бір-бірінен айырмашылығы үзілісн үетелеріндегі мәндерінде болатын түпнұсқалар жиынын сәйкес қоюға болады.
Егер
 түпнұсқасы
түпнұсқасы
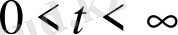 аралығында дифференциалданатын функция болса, онда берілген бейне бойынша бір ғана түпнұсқа анықталады.
аралығында дифференциалданатын функция болса, онда берілген бейне бойынша бір ғана түпнұсқа анықталады.
Мелиннің кері айналдыру формуласын тікелей қолдану қиындық туғызуы мүмкін. Сондықтан әдетте Меллин формуласының салдары болып табылатын жіктеу теоремаларын пайдаланады.
Бірінші жіктеу теоремасы
Егер
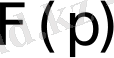 шексіз алыстағы нүктенің маңайында аналитикалық функция болып сол нүктедегі мәні 0-ге тең болса және осы нүкте маңайындағы Лоран қатарына жіктелуі
шексіз алыстағы нүктенің маңайында аналитикалық функция болып сол нүктедегі мәні 0-ге тең болса және осы нүкте маңайындағы Лоран қатарына жіктелуі
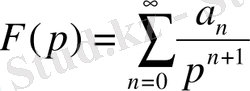 (1. 4)
(1. 4)
түрінде болса, онда
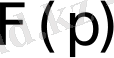 бейнесінің түпнұсқасы мына функция болады:[9]
бейнесінің түпнұсқасы мына функция болады:[9]
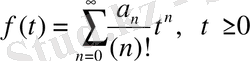 (1. 5)
(1. 5)
)
Егер
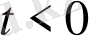 болса, онда
болса, онда
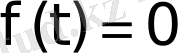 болады.
болады.
Мысал.
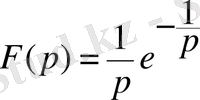 функциясының түпнұсқасын табу керек.
функциясының түпнұсқасын табу керек.
Шешуі: Берілген
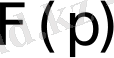 функциясының
функциясының
 нүктесінің маңайындағы жіктелуі
нүктесінің маңайындағы жіктелуі
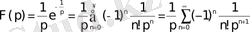
Сондықтан бірінші жіктеу теоремасы сәйкес
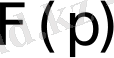 функциясының түпнұсқасы
функциясының түпнұсқасы
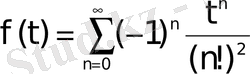 функциясы болады.
функциясы болады.
Берілген бейне бойынша түпнұсқаны табудың қарапайым әдісі
Көп жағдайларда берілген бейне бойынша түпнұсқаны табу үшін бейнені түрлендіріп, содан кейін Лаплас түрлендіруінің қасиеттерін және бейнелер кестесін пайдаланады.
Ал бейнені түрлендіру үшін көбінесе рационал бөлшектерді жай бөлшектерге жіктеу әдісі қолданылады.
Мысал 1. Берілген
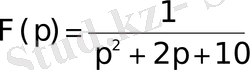 бейнесіне сәйкес түпнұсқаны табу керек.
бейнесіне сәйкес түпнұсқаны табу керек.
Шешуі:
Бірінші әдіс
Бөлшектің бөліміндегі үшмүшеліктің толық квадратын бөліп шығарып ығысу теоремасын және бейнелер кестесін пайдаланамыз
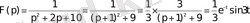
сонымен,
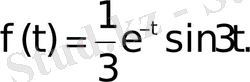
Екінші әдіс
Берілген бөлшекті жай бөлшектер қосындысына жіктейміз.
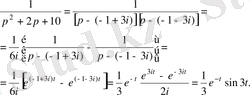
Мысал 2.
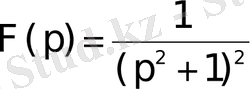 функциясының түпнұсқасын табу керек.
функциясының түпнұсқасын табу керек.
Шешуі:
Бірінші әдіс
Бөлшекті жай бөлшектер қосындысына жіктейміз
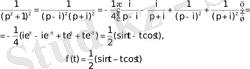
Екінші әдіс
Бөлшекті төмендегідей түрде жазайық:
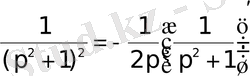
Сонда бейнені дифференциалдау теоремасы бойынша
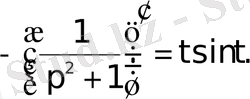
Енді түпнұсқаны интегралдау теоремасын пайдаланып, мынандай нәтиже аламыз:
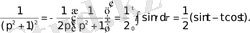
Үшінші әдіс
Функциялардың орамының бейнесі туралы теореманы қолданамыз
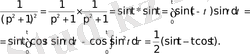
Екінші жіктеу теоремасы
Егер
 бейнесі бірмәнді функция болып және жазықтықтың бөлігінде жатқан саны шектеулі
бейнесі бірмәнді функция болып және жазықтықтың бөлігінде жатқан саны шектеулі
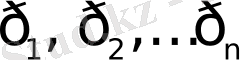 ерекше нүктелері болса, онда шегермелер туралы теореманы пайдаланып былай жазуға болады:
ерекше нүктелері болса, онда шегермелер туралы теореманы пайдаланып былай жазуға болады:
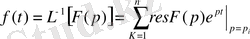 (1. 6)
(1. 6)
мұндағы
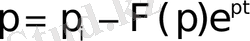 функциясының полюстері. [9]
функциясының полюстері. [9]
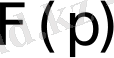 бейнесі
бейнесі
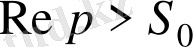 болғанда аналитикалық функция болғандықтан, көрсетілген полюстер жорымал оске параллель және одан
болғанда аналитикалық функция болғандықтан, көрсетілген полюстер жорымал оске параллель және одан
 қашықтығында өтетін түзуден солға қарай орналасқан. Егер
қашықтығында өтетін түзуден солға қарай орналасқан. Егер
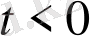 болса, онда
болса, онда
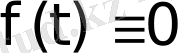 деп алу керек.
деп алу керек.
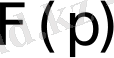 функциясы рационал функция болған жағдайды қарастырайық, яғни
функциясы рационал функция болған жағдайды қарастырайық, яғни
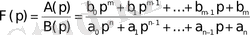 , (1. 7)
, (1. 7)
мұндағы
 және
және
 және
және
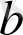 коэффициенттері нақты сандар.
коэффициенттері нақты сандар.
Бөлімінің түбірлерін есептеп, бөлшекті мына түрде жазамыз:
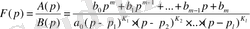 (1. 8)
(1. 8)
мұндағы
 түбірінің еселігі және
түбірінің еселігі және

Түрлендірілген (1. 8) бейненің түпнұсқасын табу үшін (1. 7)
формуланы пайдаланамыз. Полюс бойынша шегермені есептеу формуласын қолданып
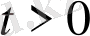 болғанда мынадай формула аламыз:
болғанда мынадай формула аламыз:
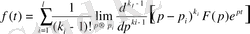 (1. 9)
(1. 9)
Дербес жағдайда, егер
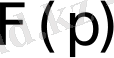 бейнесінің бөлімінің түбірлері
бейнесінің бөлімінің түбірлері
 жай түбірлер болса, онда
жай түбірлер болса, онда
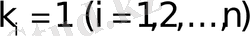 болады да, бірінші ретті жай полюс бойынша шегермені есептеу формуласын пайдаланамыз:
болады да, бірінші ретті жай полюс бойынша шегермені есептеу формуласын пайдаланамыз:
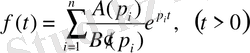 (1. 10)
(1. 10)
Мысал 1.
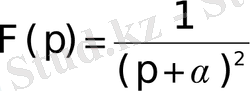 бейнесіне сәйкес түпнұсқаны табу керек.
бейнесіне сәйкес түпнұсқаны табу керек.
Шешуі: Бейненің екінші ретті
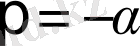 бір ғана полюсі бар.
бір ғана полюсі бар.
Формула бойынша
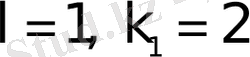 деп алып, керекті түпнұсқаны табамыз.
деп алып, керекті түпнұсқаны табамыз.
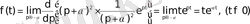
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz