Функция шектері туралы теоремалар

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 47 бет
Таңдаулыға:

Қазақстан Республикасы білім және ғылым министрлігі
Павлодар мемлекеттік педагогикалық университеті

Ж.М. Асанова

Математикалық талдау курсында функцияның шегін табудың әртүрлі әдістері

ДИПЛОМДЫҚ ЖҰМЫС

5В012600 Математика және физика мамандығы

Павлодар 2019
Қазақстан Республикасының Білім және ғылым министрлігі

Павлодар мемлекеттік педагогикалық университеті

Математика және физика кафедрасы

Қорғауға жіберілді
Математика және физика
кафедрасының меңгерушісі
_______________А.К.Киреева

ДИПЛОМДЫҚ ЖҰМЫС

Тақырыбы:
Математикалық талдау курсында функцияның шегін табудың әртүрлі әдістері

5В012600 Математика және физика мамандығы бойынша

Орындаған: МФ-41 Ж.М. Асанова

Ғылыми жетекші п.ғ.к., профессор Б.А. Найманов

Павлодар 2019
Мазмұны

Кіріспе
5
1.
Функцияның шегі

1.1
Тізбектің шегі
7
1.2
Функция шегінің екі анықтамасы және олардың парапарлығы
8
1.3
Шегі бар функциялардың қасиеттері
9
1.4
Бір жақты шектер
23
1.5
Функцияның шексіздіктегі шегі
29
1.6
Функция шектері туралы теоремалар
33
1.7
Функцияның үзіліссіздігі мен үзілуі
38
2.
Функцияның шегін табудың әртүрлі әдістері

2.1
Эквивалиетті шексіз аз шамаларды қолдану
44
2.2
Функцияның шегін табудың элементар жолдары
48
2.3
Тамаша шектер
53
2.4
Лопиталь ережесі
60

Қорытынды
65

Пайдаланған әдебиеттер тізімі
66

Кіріспе
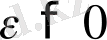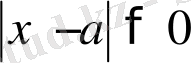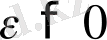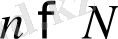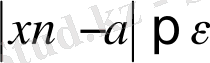Шек - математиканың негізгі ұғымдарының бірі. Егер алдын ала берілген кез келген саны үшін х айнымалы шамасының белгілі бір мәнінен бастап келесі барлық мәндері теңсіздігін қанағаттандырса, онда а саны х айнымалы шамасының шегі деп аталады.Егер кез келген аз саны үшін әрқашанда N нөмірі табылып және теңсіздігін қанағаттандыратын n-нің барлық мәндері үшін теңсіздігі орындалса, онда а саны айнымалы хn тізбегінің шегі деп аталады.
Тізбек және оның шегі ұғымдары математиканың ішкі проблемаларымен қатар оны қолдану жолында пайда болады.
Егер кез келген 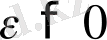аз саны үшін 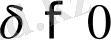саны табылып, х айнымалы шамасының 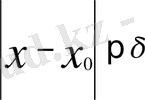теңсіздігін қанағаттандыратын барлық мәндері үшін 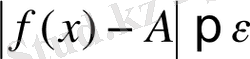теңсіздігі орындалса, онда А тұрақты саны f(х) функциясының 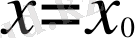нүктесіндегі шегі делінеді.Шектердің қазіргі теориясы XIX ғасырдың басында қалыптаса бастады. Шек ұғымы алғаш рет О.Коши еңбектерінде қолданылды. Тізбек пен функция шектерінің теориясы Б.Больцано мен К.Вейерштрасстың еңбектері негізінде қалыптасты.
Жинақтылық, математикада -- белгілі бір математикалық объектінің шегі болатындығын көрсететін математикалық талдаудың негізгі ұғымдарының бірі. Осы мағынада тізбектің жинақтылықтығы, қатардың жинақтылықтығы, шексіз көбейтіндінің жинақтылықтығы, үздіксіз бөлшектің жинақтылықтығы, интегралдық жинақтылық, т.б. жөнінде айтуға болады.
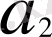,, ... нақты сандар тізбегінің жинақтылықтығы оның шекті шегі болатындығын көрсетеді: L оның шегі болса:

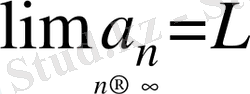
деп жазылып, "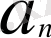тізбегі n шексіздікке ұмтылғанда L-ге тең" деп оқылады. Қандай да бір математикалық объектінің жинақтылық қасиеті математиканың теориялық мәселелері мен математика қолданылатын жерлерде елеулі рөл атқарады.
Қатарлар мен интегралдар теориясында абсолют жинақтылық ұғымының маңызы зор. Жинақтылық ұғымы әр түрлі теңдеулерді (алгебралық, дифференциалдық, интегралдық) шешуде (Мысалы, теңдеулердің сандық шешімдерін табу кезінде) үлкен рөл атқарады.
Зерттеу объектісі: жоғарғы математика курсында функцияның шегін табудың әртүрлі әдістерін баяндау.
Зерттеу пәні: математикалық талдау курсындағы функцияның шегін табудың әртүрлі әдістерін оқып үйрену, есептер шығару дағдысын дамыту үдерісі.
Зерттеудің мақсаты - жоғарғы математика курсында функцияның шегін табудың әртүрлі әдістерін анықтай отырып, кез-келген анықталмағандықты шешуді жетік үйреніп, бекіту.
Зерттеудің міндеттері:
1. Зерттеу тақырыбына байланысты әдебиеттермен танысып, оларға ғылыми-әдістемелік тұрғыдан шолу жасау;
2. Жоғарғы математика курсында функцияның шегін табудың әдістерін дәлелдеу арқылы ой-өрісті дамыту мүмкіндіктерін талдау;
3. Жоғарғы математика курсында функцияның щегін табу әдістері әдістемесін және тиімділігін тексеру.
4. оқушылардың білімділік деңгейін арттыруға бағдарланған шығармашылық тапсырмалар жүйесін әзірлеу және оны жүзеге асыру;
5. Оқушылардың білімділік деңгейін арттыруға бағдарланған шығармашылық тапсырмалар жүйесін әзірлеу және оны жүзеге асыру;
6. Шығармашылық тапсырмалар жүйесі арқылы дамуын қамтамасыз ететін педагогикалық шартты есептер кешенін анықтау, негіздеу және тексеру.
Зерттеудің болжамы: егер математикалық талдау курсындағы теориялық білімді қолдану, яғни функцияның шегін табудың әртүрлі әдістерін негіздеп, жүйелейтін болсақ, онда бұл практикалық және логикалық-дедуктивті тәсілдердің өзара байланыстарын дамытады және осы мақсатқа бағытталған оқу үдерісін қамтамасыз етеді, математикалық талдау курсын жоғары дәрежеде меңгеруге жағдайлар жасайды.
Зерттеу жұмысының теориялық және әдістемелік негіздері: білім, жеке тұлға логикасы, ақыл-ой, белсенділік туралы педагогикалық және ғылыми теориялар мен тұжырымдамалар, білім сапасы туралы теориялар.
Зерттеу әдістері: Математикалық анализ курсында функцияның шегін табу тақырыбын ойлау қабілеті жоғары дамыған балалрға түсіндерген кезде де жаңа ұғымдарды қалыптастыру үшін ерекше әдістемелік шеберлік қажет болады.
Функцияның шегі ұғымдары абрактілі. Функцияның шегін табуды оқыту нақты мысалдар қарастырудан басталады.
Функцияның шегінің анықтамалары көрнекі графиктік кескіндеудің көмегімен беріледі.

Ең алдымен шек ұғымы енгізіледі. Функцияның шегінің анықтамасын енгізбес бұрын бірнеше мысалдар қарастырылады. Сызықтық функцияның шегінен бастап, кейін күрделі функцияларды қарастыру арқылы бекітеді
Зерттеудің ғылыми жаңалығы:
- жоғарғы математикада шектерді оқытуда оқушылардың математикалық талдау курсына деген қызығушылығын шектерді табудың әдісері арқылы дамытудың ғылыми-әдістемелік тұрғыдан негіздеді;
- функцияның шегі және оны табудың ерекшеліктері мен оларға сәйкес әдістемелік талаптарын анықтау, оларға сай есептер анықталады;
- функцияның шектерін табуды оқыту үрдісінде қолдану арқылы күрделі, қиын деп саналатын есептерді шешуге баулу, сол арқылы оқушылардың математикалық талдау сауаттылығын жетілдіріп дамытады.
Зерттеу жұмыстың құрылымы мен көлемі. Диссертация кіріспеден, екі тараудан, қорытынды және пайдаланылған әдебиеттер тізімінен тұрады.

1 Функцияның шегі

1.1 Тізбектің шегі
Сандық тізбек, оның берілу тәсілдері және графикпен бейнеленуі
Сандық тізбек деп N натурал сандар жиынында анықталған сандық функцияны (немес N жиынының R жиынына бейнеленуін) атайды. Бұл функцияның f әріпімен белгілейік. Сонда анықтама бойынша 1 санына f(1) мәні, 2 санына f(2) мәні т.с.с. сәйкес келеді. Жалпы алғанда ондай сәйкестікті былай белгілейді:
n -- f(n).
Бұл шамаларды сәйкес түрде f1= f(1), f2= f(2),..., fn= f(n),... арқылы белгілеп, оларды тізбектің бірінші, екінші, және т.с.с. n - ші мүшелері деп атайды, n - ші мүшені тізбектің жалпы мүшесі дейді. Жалпы мүшесі fn болатын тізбекті f1,f2,...,fn,... немесе fn арқылы белгілейді. Осылайша белгілеуде n номері N натурал сандар жиынының барлық мәндерін қабылдайды деп түсініледі.
Тізбекті жазып берудің жиі қолданылатын тәсілдері мыналар:
1. Аналитикалық тәсіл. Бұл тәсілді қолданғанда n номері бойынша тізбектің сәйкес мүшесін табу үшін формула жазылып көрсетіледі.
Мысалдар: 1. xn= 1+12n(n) (n N) . Бұл формула бойынша
x1 = 1 + 12 =32 , ..., x5 = 1 + 125 = 1+132 = 3332 , т.с.с. Бұл жағдайда xn тізбегі
xn = 1 + 12n формуласымен берілген дейік.
2. xn = 3, n N. Бұл тізбектің барлық мүшелері бір- бірімен тең. Барлық мүшелері өзара тең болатын тізбекті тұрақты тізбек деп атайды.
3. Тізбекке тағы мынадай мысалдар келтірейік:
n = 1, 2, 3,...,n,...; 1n = 1, 12, 13,...,1n,...;
1+ 110n =1,1;1,01;1,001;...;1+110n; n-1n = 0, 12,23,... .
2. Рекурренттік тәсіл. Бұл тәсілді қолданғанда тізбектің бірінші мүшесі беріледі және осы тізбектің белгілі бір неме бірнеше алғашқы мүшелері бойынша кез- келген мүшесін табу үшін формула беріледі.
Мысал. а) кез келген n = 2 үшін an= an-1+d ; б) кез- келген n = 2 үшін bn= bn-1*q ; а) және б) формулалары сәйкес an және bn тізбектерінің берілген алдыңғы мүшесі бойынша оның кез келген мүшесін (екінші мүшесінен бастап) табуға мүмкіндік береді. Бұл тізбектер арифметикалық және геометриялық прогрессиялар түрінде бізге бұрыннан таныс болатын. Тізбектің рекурренттік тәсілмен берілуі шапшаң есептейтін электрондық есептеуіш машиналармен жұмыс істегенде аса қолайлы келеді; сонда машина әрі жеңіл, әрі шапшаң орындалатын біріңғай есептеу операцияларын бірнеше рет қайталайтын болады.
3. Баяндап беру тәсілі. Бұл тәсілді қолданғанда тізбек элементтері баяндап айтылатын болады. Бұл жағдайда тізбектің жалпы мүшесі үшін формула да, немесе оның мүшелері үшін рекуренттік қатыс та белгісіз болуы мүмкін. Осы айтылғанды мысалмен түсіндіру үшін мына тізбектерді қарастырайық.
а) 2, 3, 5, 7, 11,...; б) 2; 2,2; 2,23; 2,236; 2,2361; ... Бұл тізбектерді былайша баяндайды: бірінші тізбек жәй сандар тізбегі, ал екіншісі 5 саны үшін кемімен алынған ондық жуықтаулар тізбегі.
yn тізбегін графикпен бейнелегенде мынадай екі тәсіл қолданылады:
1) yn тізбегін функция деп алып, оны координаталық жазықтықтың M(n, yn) нүктелерінің жиыны арқылы бейнелуге болады;
2) yn тізбегін координаталық түзудің M(yn) (немесе yn ) нүктелерімен бейнелеуге болады.
yn = 1n тізбегін бейнелеудің осы екі тәсілі де 28, 29- суреттерде көрсетілген.
y

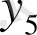
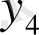
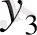
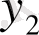
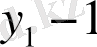
О 0 1 у
0 1 2 3 4 5 x

Тізбек шегін анықтау
1- анықтама. Егер кез келген оң ԑ санына сайкес натурал nƐ саны табылып, барлық n ˃ nԑ номерлері үшін xn-a˂ ԑ теңсіздігі орындалса, онда a саны xn тізбегінің шегі деп аталады және былай жазылады: limn--infinityxn= a немесе n--infinity (символдар арқылы:
limn--infinityxn ⇔∀ԑ ˃ 0 nԑǀn˃ nԑ⇒ǀxn-aǀ˂ԑ). Шегі бар болатын тізбек жинақталатын тізбек деп, ал шегі болмайтын тізбек жинақталмайтын тізбек деп аталады. Модуль қасиетінің негізінде ǀxn-aǀ˂ԑ теңсіздігі -ԑ ˂xn- a˂ ԑ немесе a-ԑ˂xn˂ a+ԑ теңсіздігімен пара пар, олай болса, барлық n ˃ nԑ үшін xn∈ Uԑ(a), яғни a нүктесінің ԑ- маңайы тізбектің n ˃ nԑ нөмірлі барлық мүшелерін қамтиды. Бұдан тізбек шегінің тағы бір анықтамасына келеміз.
2- анықтама. Егер a нүктесінің кез- келген ԑ маңайы xn тізбегінің саны арқылы x1,x2,...,xnԑ мүшелерінен өзге барлық мүшелерін қамтитын болса, онда осы a санын xn тізбегінің шегі деп атайды.

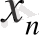
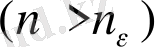
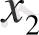
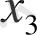
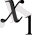
Мысал. 1. n-1n+1 тізбегі жинақталады және оның шегі 1 - ге тең. Шынында да, шек анықтамасының орындалатындығын тексерейік. Ол үшін n-1n+1-1 ˂ ԑ теңсіздігін қарастырайық. Кейбір түрлендірулерді орындай келе мынаны табамыз:
n-1n+1-1 ˂ ԑ⇔2n+1 ˂ ԑ ⇔ n+12 ˃ 1ԑ ⇔ n ˃ 2ԑ - 1.

Демек, натурал nԑ саны табылып, (мысалы, 2ԑ -1 санының бүтін бөлігіне тең), барлық n ˃ nԑ= 2ԑ - 1 нөмірлері үшін n-1n+1-1 ˂ ԑ теңсіздігі орындалады, яғни limn--infinityn-1n+1 = 1. Енді ԑ = 0.01 және ԑ = 0.001 мәндеріне сәйкес nԑ мәндерін табайық.
а) ԑ = 0.01 ; nԑ = (2 . 102- 1)= 200 - 1= 199; nԑ = 199.
б) ԑ = 0.001 ; nԑ = (2 . 103- 1)= 2000 - 1= 1999;
n--infinity жағдайда n-1n+1 бөлшегі бірден кіші мәндерді қадһбылдай отырып, өсе келе 1 санына ұмтылады, яғни n-1n+1 -- 1.
Мысал-2. limn--infinitycosPI2nn = 0. Шынында да, cosPI2nn-0 = 1n ԑ ⇔ 1ԑ . Демек , n ˃ nԑ = 1ԑ ⇔ cosPI2nn-0 ԑ . n--infinity жағдайда cosPI2nn бөлшегі 0- ге тең де, одан кіші де мәндерді қабылдай отырып, өзінің шегі 0- ге ұмтылады .
Мысал-3. cosPI2n жинақталмайтын тізбек болады. Шынында да, a нүктесінің ԑ- маңайының сыртында осы тізбектің сансыз көп мүшелері жатады. Сондықтан a саны тізбектің шегі бола алмайды.
Тізбектің шегі туралы теоремалар
1- теорема. Егер xn және yn тізбектері жинақталатын болса, онда xn+-yn тізбектері де жинақталатын болады және limn--infinity(xn+-yn) = limn--infinityxn + limn--infinityyn, яғни жинақталатын екі тізбек қосындысының шегі сол тізбектер шектерінің қосындысына тең болады.
Дәлелдеуі. limn--infinityxn = a және limn--infinityyn=b дейік. Сонда1- теорема (6-п.) негізінде xn=a + αn, yn= b + βn (мұндағыαn мен βn ақырсыз кіші тізбектер) теңдіктерін аламыз. Бұдан xn+-yn = (a + b) + (αn+ βn). xn+-yn тізбегі 1- лемма негізінде ақырсыз кіші тізбек, яғни limn--infinity(xn+-yn)= 0. Сонда 6- пункттің 1- теоремасы бойынша limn--infinity(xn+-yn) = limn--infinityxn + limn--infinityyn. Бұл теореманы индукция әдісін қолдана отырып, саны шектеулі тізбектердің алгебралық қосындысы үшін де дәлелдеуге болады.
2- теорема. Егер xn және yn жинақталатын тізбек болса, онда xn∙yn тізбегі де жинақталатын болады және
limn--infinity(xn∙yn) = limn--infinityxn ∙ limn--infinityyn, яғни жинақталатын тізбектер көбейтіндісінің шегі олардың шектерінің көбейтіндісіне тең болады.
Дәлелдеуі. limn--infinityxn = a және limn--infinityyn=b болсын, сонда xn=a + αn, yn= b + βn (мұндағыαn мен βn ақырсыз кіші тізбектер). Мына көбейтіндіні қарастырайық:
xn∙yn=(a + αn)(b+ βn) = ab+(aβn+bαn+αnβn) ; aβn+bαn+αnβn тізбегі 1 және 2- леммалар негізінде ақырсыз кіші тізбек болып табылады. Сонымен, барлық n ∈ N үшін
xn∙yn= ab+(aβn+bαn+αnβn),
limn--infinity(aβn+bαn+αnβn) = 0. Ал бұдан мына теңдік шығады (1- теореманы қараңыз):
limn--infinity(xn∙yn) = limn--infinityxn ∙ limn--infinityyn.

Ескерту. Егер барлық n ∈ N үшін xn= С болса, онда limn--infinityxn =limn--infinityС =С немесе тұрақты санның шегі десол тұрақты сан болады. Шынында да, xn-С=С-С=0 болғандықтан, xn-С ақырсыз кіші тізбек, сондықтан 1- теорема бойынша limn--infinityxn = С.
1- салдар. Егер xn тізбегі жинақталатын болса, онда кез келген С саны үшін С∙xn тізбегі де жинақталатын тізбек болады және limn--infinityС∙xn= limn--infinityС ∙ limn--infinityxn = С∙limn--infinityxn , яғни тұрақты көбейткішті шек таңбасының алдына шығаруға болады.
2- салдар. Егер xn тізбегі жинақталатын тізбек, ал k- натурал сан болса онда
limn--infinityxnk= (limn--infinityxn)k .
Бұл салдарды 2- теоремадан индукция әдісін қолдана отырып алуға болады.
3- теорема. Егер xn және yn, yn!= 0, тізбектері жинақталатын болып, сонымен бірге, limn--infinityyn != 0 болса, онда xnyn тізбегі жинақталатын тізбек болады да limn--infinityxnyn = limn--infinityxnlimn--infinityyn теңдігі орындалады. Алдын ала мына лемманы дәлелдейік.
Лемма. Егер yn тізбегі ( yn!= 0) жинақталатын болып, сонымен бірге, limn--infinityyn != 0 болса, онда n0 нөмірі табылып, барлық n ˃ n0 нөмірлері үшін 1yn тізбегі шенделген тізбек болады.
Дәлелдеуі. Анықтама бойынша
limn--infinityyn=b ⇔ ∀ԑ 0 ∃ n0⃒ n ˃ n0⇒ yn-b=b- ynԑ .
Енді ԑ=b2 деп алып, айырма модулінің қасиетін пайдаланып, алдыңғы теңсіздікті мына түрде жазайық: b2 b- yn =b- yn, n ˃ n0 . Бұдан yn b2 теңсіздігі шығады, ал шарт бойынша yn!= 0 болғандықтан, барлық (n ˃ n0) нөмірлері үшін 1yn b2 теңсіздігі орындалады.
3- теореманы дәлелдеуге көшейік. limn--infinityxn = a, limn--infinityyn=b деп алайық. Теореманы дәлелдеу үшін (6-п, 1- теорема бойынша) xnyn - 2b айырымы ақырсыз кіші екенін дәлелдеу жеткілікті. Бізге мына теғдіктер белгілі:
limn--infinityxn = a⇔ xn=a + αn, limn--infinityαn = 0 ;
limn--infinityyn=b ⇔ yn= b + βn, limn--infinityβn = 0 .
Осыларды пайдаланып табатынымыз:
xnyn- ab=1yn·xn-abyn=1yn·a + αn-ab(b + βn) =1yn·αn-ab βn ,
мұндағы1yn тізбегі лемма бойынша шенделген, ал αn-ab βn ақырсыз кіші тізбек (7- п, 1-2 леммалар). 1yn(αn-ab βn) ақырсыз кіші тізбек (7-п,2- лемма). Сондықтан xnyn- ab айрймы ақырсыз кіші тізбек болады. Бұдан мына теңдік шығады (6-п, 1- теорема):
limn--infinityxnyn= ab = limn--infinityxn limn--infinityyn .
1.2 Функция шегінің екі анықтамасы және олардың парапарлығы

a нүктесінің қандай болмасын (c,d) маңайында анықталған f функциясын қарастырайық.
1-анықтама.Егер а санына жинақталатын кез келген {xn}үшін f функциясы мәндерінің сәйкес {f(xn)} тізбегі А санына жинақталатын болса,онда А санын f функциясының х-тің а-ға ұмтылғандағы шегі деп атайды және былай белгіленеді:
A=limx--af(x) (1)
немесе x--a жағдайда f(x) --A (символдар арқылы:
A=limx--af(x)--∀xn,xn!=axn--a= fxn--A,n∈N).
Ескерту.1-анықтама бойынша функцияның шегі біреу ғана болатыны шығады.
2-анықтама.Егер кез келген ε0 санына сәйкес δ0 саны табылып,0x-aδ шартын қанағаттандыратын барлық х үшін fx-Aε теңсіздігі орындалса,онда А саны f функциясының x-тің a-ға ұмтылғандағы шегі деп атайды және (1) өрнегімен белгілейді(символдар арқылы:
A=limx--af(x)--∀ε0,0x-aδ--fx- Aε).
Егер нүкте маңайының белгілеуін пайдалансақ,былай жазуға болады:
A=limx--afx--∀ε0 ∃δ=δε0 x∈Uδ0a--fx∈UεA.
яғни кез келген ε0 үшін δ=δ(ε)0 саны табылып,аргумент мәндері а нүктесінің ортасынан δ маңайына тиісті болғанда f функциясының сәйкес мәндері А нүктесінің ε маңайына тиісті болады(1-сурет).Енді осы екі анықтаманың пара-парлығын дәлелдейік.1-анықтамада айтылған мағынада A=limx--afx болсын,сонда осы шектің 2-анықтамада айтылған мағынада да бар болатынын көрсетейік.Қарсы жорып,екінші анықтама дұрыс болмайды дейік.Бұл жорамалды әдеткі ∀ символын ∃ символымен , ∃ символын ∀ символымен,яғни, "барлық х үшін" сөз тіркесін "x0 мәні табылады" сөз тіркесімен алмастыра отырып,керісінше тұжырымдап,2-анықтаманы теріске шығарайық.

y
A+ε
A
A- ε

0 a-δ a a+δ x
1-сурет.
Сонда∃ε00∀δ0∃xδ0xδ-aδ--fxδ-A= ε0, немесе ε00 саны табылып,кез келген δ0 саны үшін ең болмағанда бір xδ нүктесін табуға болады және 0xδ-aδ теңсіздігі орындалғанда fxδ-A=ε0 теңсіздігі де орындалады.
δ саны үшін 1k,k∈N тізбегінің барлық мүшелерін алайық. Сонда әрбір δk=1k және оған сәйкес xk нүктесі үшін 0xk-a1k теңсіздігінен fxk-A=ε0 теңсіздігі шығады.Алайда xk--a жағдайда оған сәйкес мәндерінің f(xk) тізбегі А санына ұмтылмайды.1-анықтаманың мағынасына қарай осы табылған қайшылық айтылған болжамды дәлеледейді.
Енді 2-анықтамада "ε-δ" тілінде айтылған мағынадағы f функциясының шегі 1-анықтамада айтылған мағынада да бар болатынын көрсетеміз.Ол үшін ε0 санын тағайындап алып ,оған сәйкес δ санын табамыз. Енді xn xn!=a,n∈N a санына ұмтылатын қандай да болсын тізбек дейік (xn--a).Сонда δ0 санына сәйкес n0 нөмірі табылып,барлық nn0 үшін 0xn-aδ теңсіздігі орындалады.Бұдан 2-анықтама бойынша f(xn-A)ε теңсіздігі шығады.Сонымен xn--a жағдайда f(xn)--A болады.Осының өзі бірінші анықтаманың дұрыс екенін көрсетеді.Демек,функция шегінің екі анықтамасы бір-бірімен пара-пар болып шықты.Бұл ек анықтаманың қай-қайсысына да қолайлы болған кезде пайдалана беруге болады.
Функцияның нүктедегі шегінің бір- бірімен эквивалентті екі анықтамасын келтірейік.
1- анықтама. (функция шегінің Коши бойынша анықтамасы немесе ≪ε-δ тілінде≫) .
Егер f фуекциясы x0 нүктесінің кейбір аймағында анықталса, мүмкін, осы x0 нүктеден басқа, және кез келген ε 0 санына δ(x0, ε) 0 саны табылып, 0 x-x0δ шартын қанағаттандыратын барлық x үшін мына теңсіздік орындалса
fx-A ε,
Онда A саны f функцисының x0 нүктесіндегі шегі деп аталады.
Функцияның шегін limx-x0fx =A немесе fx--A (x--x0) деп белгілейміз.
Бұл анықтаманы қысқаша былай жазуға болады

limx-x0fx =A⇔(∀ԑ 0)(∃δ0)(∀x : 0x-x0δ ): fx-Aε (3.2)
немесе
limx-x0fx =A⇔(∀ԑ 0)(∃δ0) (∀x ∈δ0(x0)): fx-Aε

2- анықтама. (Функция шегінің Гейне бойынша анықтамасы).
Егер f функциясы x0 нүктесінің кейбір аймағында анықталса, мүмкін, осы x0 нүктеден басқа, және осы x0 нүктесіне жинақталатын кез келген xn, xn !=x0, тізбекке сәйкес функция мәндерен тұратын fxn тізбектің шегі A болса n--infinity, яғни мына теңсіздік орындалса
limn--infinityfxn =A
онда A саны f функцисының x0 нүктесіндегі шегі деп аталады.
Бұл анықтаманы қысқаша былай жазуға болады

limx-x0fx =A⇔(∀xn)( limn--infinityxn =x0, xn !=x0): limn--infinityxn =A.

Мысал fx= sin1x функцияның x--x0 шегі бар ма?
Шешімі. Кез келген екі тізбекті қарастырайық xnʹ = 1PIn және xnʹʹ = 1PI2+2PIn.
Бұл екі тізбектің шектері нөлге тең, яғни limn--infinityxnʹ =0, limn--infinityxnʹʹ =0, бірақ xnʹ!=0, xnʹʹ!=0, ∀ n.
Сонымен fxnʹ= sinPIn=0, n=1,2,..., fxnʹʹ= sinPI2+2PIn=1,
n=1,2,...,
Сондықтан limn--infinityfxnʹ= 0, limn--infinityfxnʹʹ= 1.
fx= sin1x функцияның x--x0 шегі жоқ.
fx функциясының x--x0 шегі бар себебі функцияның мәндерінен құрылған тізбектің шегі fxn тізбекті қалай алсақта n--infinity ұмтылғанда бірге тең.
Функцияның шегін анықтаңыз:

Мысалдар.1.fx=cos1x.Бұл функцияның limx--0fx шегі бар бола ма, соны тексерейік.Ол үшін мынадай екі тізбекті қарастырайық: xn=12PIn және
x'n=1PI2+PIn,n∈N. Бұдан
limn--infinityxn=limn--infinityx' n=0xn!=0,x'n!=0; fxn=cos2PIn=1, fx'n=cosPI2+PIn=0,n∈N.Сондықтан,lim n--infinityfxn=1 және limn--infinityfx'n=0,олай болса limx--0f(x) шегінің мәні жоқ болып шықты.
2. fx=x2-9x-3. Бұл функция барлық x!=3 мәндерінде анықталған.limx--3f(x) шегін табайық.Барлық x!=3 үшін x2-9x-3=x+3,x--3 жағдайда f функциясының шегін тапқанда x=3 нүктесіндегі мәні ескерілмейтін болғандықтан,limx--3x2-9x-3=limx-- 3(x+3)=limx--3x+3=3+3=6.Бұл жерде біз limxx--3=3 мәнін пайдаландық.Шынында,кез келген xn ,мұндағы xn!=3,n∈N,xn--3 тізбегін алу жеткілікті.Сонда функцияның сәйкес мәндер тізбегі алынған xn тізбегімен сәйкес келеді де, функция шегі 6 санына тең болады. fx=x2-9x-3 және φx=x+3 функциялары әр басқа функциялар екендігін ескертеміз. Бірінші функция барлық x!=3 мәндерінде анықталған да , екіншісі барлық x∈R мәндерінде анықталған.Алайда x--3 жағдайда ол функциялардың шегін тапқанда x=3 нүктесінде функцияның анықталған-анықталмағандығына мән берілмейді. x!=3 болғанда fx=φ(x) болғандықтан,limx--3fx=limx--3φx.
Бөлшектерді қысқарту арқылы анықталмағандықтарды айқындау ережесі осы келтірілген ескертуге негізделген.
3. limx--2x2=4. Егер n--infinity жағдайда xn--2(xn!=2) болса,онда limn--infinityxn2=limn--infinityx n∙limn--infinityxn=2∙2=4.Бұл тұжырымды дәлелдеу үшін шектің 2-анықтамасын пайдаланамыз.Ол үшін x=2 нүктесін қамтитын қандай болмасын бір интервалды,мысалы (32;52) интервалын,қарастырайық.Сонда кез келген x∈32;52 үшін x+292 теңсіздігі орындалады. Сондықтан x2-4=x-2∙x+24,5∙x-2.
Енді ε-ді қалауымызша таңдап алып,δ-ны 12 мен 2ε9 сандарының ең кішісіне тең етіп аламыз.Сонда x-2δ теңсіздігін қанағаттандыратын x-2δ теңсіздігін қанағаттандыратын барлық х үшін x-20
1.3 Шегі бар функциялардың қасиеттері
а саны f(х) функцияның анықталу облысының шектік нүктесі болсын.
Функцияның шегіне тəн келесі қасиеттерді дəлелдеуге болады.
1) Егер тəуелсіз айнымалы х, а санына ұмтылғанда, функция f(х) b санына ұмтылса жəне bА болса (мұнда А-тұрақты), онда осы а санына өте жақын, бірақ оған тең емес х-тің мəндері үшін функция f(х) төмендегі теңсіздікті

f(х)A
қанағаттандырады.
Бұл теореманы дəлелдеу үшін алдын ала берілетін оң ε санын былай сайлап алайық: ε b−А, бұл арадан,

b −ε А.
Функция шегінің анықтамасы бойынша осы берілген ε саны бойынша δ саны табылып,
x-aδ
теңсіздік орындалысымен мына теңсіздік

fх-bε
орындалуы керек. Ал кейінгі теңсіздік мынадай

b - ε fх b + ε
қос теңсіздікпен парапарлығы бізге белгілі. х-тің а-ға өте жуық мəндері үшін теңсіздік орындалатын болды: олай болса х-тің бұл мəндері үшін теңсіздік сөзсіз орындалады.
Сонымен, теорема немесе қасиет дəлелденді.
Егер bВ болса, онда функция f(х) тəуелсіз айнымалы x-тің а санына тым жуық мəндері үшін мына теңсіздікті f(х)В қанағаттандырады.
2) Егер тəуелсіз айнымалы х, а-ға ұмтылғанда, функция f(х) шекке ұмтылса, онда х-тің а санына тым жуық мəндері үшін функцияның өзі де оң болады егер функция теріс шекке ұмтылса, онда функция да теріс болады.
3) Егер айнымалы х тұрақты а санына ұмтылғанда, функция f(х) шектеулі b' санына ұмтылса, онда х-тің а-ға тым жуық мəндері үшін функция шектелген болады, былайша айтқанда оның абсолют шамасы бір тұрақты М санынан асып кетпейді, яғни

fх=M, мұнда x-a=δ.
Айтылып отырған қасиеттің дұрыстығы (16) теңсіздіктен-ақ көрініп тұр.
4) Саны шектеулі функциялардың алгебралық қосындысының шегі олардың шектерінің қосындысына тең. Бұл қасиетті екі функция үшін дəлелдейік.
Айталық,

limx--afx= b, limx--aφx= c,
Онда

limx--afx+φφ= limx--afx+limx--aφx=b+c.
Міне, осыны дәлелдеу керек.
Теореманың шарттары бойыншамына теңсіздікті

x-aδ
қанағаттандыратын барлық х-тер үшін келесі теңсіздіктер

fх-bε2, φx-сε2
орындалуы керек.
Мына теңбе - теңдікті

fx+φφ-b+c= fх-b+ φx-с

қарайық .Ал

fx+φφ-b+c=fх-b+φx-с.
(17) теңсіздіктерді еске алсақ,

fx+φφ-b+cε2+ε2 = ε,
Кейінгі теңсіздіктің орындалуы теореманың дұрыстығын дəлелдейді.
5) Саны шектеулі функциялардың көбейтіндісінің шегі олардың шектерінің көбейтіндісіне тең.
Айталық,

limx--afx= b, limx--aφx= c,
Сонда

limx--afx · φφ= limx--afx · limx--aφx=b · c.
Осыны дəлелдеу керек.
Теореманың шарттары бойынша алдын ала берілген оң құнарсыз аз ε санына сəйкес δ саны табылып, мына теңсіздіктің (х−а)δ орындалуынан келесі тенсіздіктер

fх-bε2с, φx-сε2М
Орындалады, мұнда М - тұрақты оң сан.
3) Қасиет бойынша мына теңсіздікті x-aδ қанағаттандыратын барлық х- тер үшін төмендегі теңсіздік

fх=M
орындалуға тиіс.
Келесі тепе- теңдікті

fxφφ-bc= fxφx-с +сfх-b
қарайық . Абсолют шама жөніндегі қаралып өткен теорема бойынша

fxφφ-bc=fxφx-с+сfх-b.
(18) және (19) теңсіздіктерді еске алсақ,

fxφφ-bcε2+ε2 = ε.
Бұл теңсіздіктің орындалуы теореманы дəлелдейді.
Осы дəлелденген теоремадан мына салдар келіп туады: тұрақты санды шек таңбасының сыртына шығаруға немесе оның ішіне еңгізуге болады, яғни

limx--akfx=k limx--afx.
6) Екі функцияның бөліндісінің шегі олардың шектерінің бөліндісіне тең (егер бөлгіш функцияның шегі нольге тең болмаса).
Айталық,

limx--afx= b, limx--aφx= c, (c!=0)
онда,

limx--afxφx = limx--afxlimx--aφx = bс.
Теореманың шарты бойынша алдын ала берілген оң ε санына сәйкес δ саны табылып мына теңсіздіктің x-aδ орындалуынан мына теңсіздік

φx-с ε немесе с - ε φx с + ε
орындалады. Кейінгі теңсіздіктен мынаны табамыз

1с - ε1φx1с+ε
Бұл арадан мынадай қортындыға келеміз:
(а−δ, а+δ), аймақтың ішінде жатқан барлық х-тер үшін функция шектелген, былайша айтқанда

1φx=М
мұнда М - тұрақты оң сан.
Енді мына айырманы қарайық 1φx-1с қарайық:

1φx-1с =с-φx с · φx
бұл арадан

1φx-1с =1сφxφx-с.
(20) жəне (21) теңсіздіктерді еске алсақ, онда (а−δ, а+δ) аймақтың барлық нүктелері үшін төмендегі теңсіздік орындалады:

1φx-1с Мεс
ε- ең құнарсыз аз сан, сондықтан

limx--a1φx = 1с = 1 limx--aφx
Енді fxφx бөліндіні мына түрде жазуға болады

fxφx = fx·1φx.
(23) теңдіктің оң жағын екі функцияның көбейтіндісі деп қарауға болады. Ендеше оған (5) қасиетті қолданамыз, сонда

limx--afxφx = limx--afx· limx--a1φx.
(22) теңсіздікті еске алып табамыз:

limx--afxφx = limx--afxlimx--0φx
Сонымен , теорема дəлелденді.
Біркелкі функцияның шегі туралы төмендегі теореманы дəлелдейік.
7) а берілген біркелкі f(х) функцияның анықталу облысының шектік нүктесі болсын жəне бұл сан х-тің барлық мəндерінен үлкен болсын. Сонда, егер үдеме функция f(х) жоғары, жағынан шектелген болса, яғни

f(х) = М,
онда тəуелсіз айнымалы х, а санына ұмтылғанда айтылып отырған функцияның шектеулі шегі болады.
Функция f(х) жоғарғы жағынан шектелгендіктен, оның өз анықталу облысында қабылдайтын мəндерінің жиыны жоғарғы жағынан шектелген жиын болып табылады. Сондықтан жиынның дəл жоғарғы шекаралығы болады, оны біз L арқылы белгілейік.
Жоғарғы шекаралықтың қасиеті бойынша оң ε саны қаншама шама аз болса да функцияның анықталу облысында жатқан жəне а санынан кіші х' мəн (х'а) үшін, төмендегі теңсіздік:

fxʹL-ε
орындалуға тиіс. Функция f(х) үдеме болғандықтан, х х болғанда
f(х) f(x') болады. Ендеше

fxL-ε
Екінші жағынан

fx=L L+ε.
Сөйтіп тəуелсіз айнымалы х-тің а санына аса жақын мəндері үшін, функция f(х) келесі теңсіздікті

L-ε fx L+ε
Немесе fx-L ε қанағаттандырады.
Кейінгі теңсіздіктің орындалуы теореманың дұрыстығын дəлелдейді.
Осы дəлелденген теорема біркелкі кеміме функция үшін де дұрыс болатындығын оқушылардың өздері де дəлелдей алады.
2. Функцияның ең үлкен жəне ең кіші шектері туралы бір екі ауыз сөз айта кетейік.
Тəуелсіз айнымалы х тұрақты а санына ұмтылғанда f(х) функцияның тиянақты шегі болмағанымен, осы а санына жинақталымды жеке x1 ,x2,..., x3,...--a тізбектер үшін мына шектің limn--infinityfxn= болуы мүмкін: бұл шекті бөлімше шек деп атайды.
Функцияның бөлімше шектерінің ішінен ең үлкенін жəне ең кішісін табуға болады; бұларды былай белгілейміз:

limx--afx, limx--afx.
Функцияның тиянақты шегі болу үшін оның ең үлкен шегі мен ең кіші шегінің өзара тең болуы қажетті жəне жеткілікті.
1.4 Бір жақты шектер.
f функциясы (c ,d] жарты интервалда анықталған дейік.
1-анықтама. Егер а санына жинақталатын кез келген {xn}, мұндағы xna,n∈N,тізбегіне f функциясы мәндерінің сәйкес {f(xn)} тізбегі А санына жинақталатын болса,онда А саны х-тің а-ға ұмтылғандағы f функциясының сол жақты шегі деп аталады және былай жазылады:
A=limx--a-0f(x)
(символдар арқылы:
A=limx--a-0 f(x)--∀xnan∈Nxn--a=f(xn)--A).
2-анықтама.Егер кез келген ε0 үшін оған тәуелді δ0 саны табылып,a-δxa теңсіздігін қанағаттандыратын барлық х үшін fx-Aε теңсіздігі орындалса,онда А саны х-тің а-ға ұмтылғандағы f функциясының сол жақты шегі деп аталады және былай жазылады:
A=limx--a-0f(x)
(символдар арқылы: A=limx--a-0 f(x)--∀ε0 ∃δ=δ(ε)0a-δxa=fx-Aε).
1 және 2-анықтамалардың мәндестігін 1-пункттегідей дәлелдеуге болады.Жоғарыда келтірілген анықтамаларға ұқсас түрде х-тің а-ға ұмтылғандағы f функциясының оң жақты шегінің 1 және 2-анықтамаларын тұжырымдауға болады.Ол шекті limx--a+0f(x) арқылы белгілеп,символдар арқылы жазып көрсетейік.
1. A=limx--a+0fx=∀xn,xna(n∈N)xn--a =fxn--A.
2. A=limx--a+0fx=∀ε0 ∃δ=δε0
axa+δ=fx-Aε.
Егер а=0 болса,онда x--0-0 орнына x--0+0 орнына x--+0 деп жазады.
Мысал. fx=xx.Бұл функцияның limx---0fx және limx--+0f(x) шектерін табайық. 1-анықтаманы пайдаланамыз.Кез келгенx'nжәне xn тізбектері мына шарттарды: x'n0,xn0(n∈N),limn--infinityx'n= limn--infinityxn=0 қанағаттандырады дейік. Сондa

limn--infinityfx'n=limn--infinity x'nx'n=limn--infinity-x'nxn=-1; limn--infinityfxn=limn--infinityx nxn=limn--infinityxnxn=1.
Бұдан limx---0fx=-1, limx--+0fx=1. x--a жағдайдағы f функциясының (екі жақты) шегі мен оның бір жақты шектерінің арасындағы байланысты мына теорема арқылы тұжырымдайды.
Теорема.A=limx--afx болуы үшін limx--a-0fx=limx--a+0f(x) болуы қажетті және ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.