Салу есептерін шығарудың негізгі кезеңдері

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 53 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

Академик Ә.Қуатбеков атындағы Халықтар Достығы
университеті

Информатика және математика кафедрасы

Қорғауға жіберілсін
__________кафедра меңгерушісі
ф.-м.ғ.к., профессор Юнусов А.А.
_____________2019 ж.

ДИПЛОМ ЖҰМЫСЫ

Жұмыстың тақырыбы: Мектеп геометрия оқулықтарындағы салу есептері және оны шығару әдістері

Мамандығы: 5В010900 - Математика

Орындаған: Т109-15 Балтабай Е.Н.

Дипломдық жұмыстың
жетекшісі: доцент Қарабаев А.

Шымкент - 2019
МАЗМҰНЫ

КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...

1 МЕКТЕП ГЕОМЕТРИЯ ОҚУЛЫҚТАРЫНДАҒЫ САЛУ
ЕСЕПТЕРІ ЖӘНЕ ОЛАРДЫ ШЫҒАРУ ӘДІСТЕРІ ... ... ... ... ... ... ..

1.1 Жазықтықтағы негізгі салу есептері ... ... ... ... ... ... ... ... ... ... ... ... ..
1.2 Салу есептерін шығарудың негізгі кезеңдері ... ... ... ... ... ... .. ... ... .
1.3 Планимертиялық салу есептерін шығарудың негізгі әдістері ... ...
1.3.1 Симметрия әдісі ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ...
1.3.2 Түзулеу әдісі ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
1.3.3 Қиылысу әдісі ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ...
1.3.4 Ұқсастық және гомотетия әдісі ... ... ... ... ... ... ... .. ... ... ... ... ... ... .
1.3.5 Паралель көшіру әдісі ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... .
1.3.6 Алгебралық әдісі ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... .

2 НҮКТЕЛЕРДІҢ ГЕОМЕТРИЯЛЫҚ ОРНЫНА (Н.Г.О)
БЕРІЛГЕН САЛУ ЕСЕПТЕРІ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..

2.1 Жазықтықта ортақ қасиеті бар нүктелер жиыны ... ... ... ... ... ... ...
2.2 Н.Г.О әдісін салу есептерін шығаруда қолдану ... ... ... ... ... ... ... ..
2.3 7-9 Сынып геометрия оқулықтарындағы нго әдісімен
шығарылатын салу есептерін шығару және нго берілген
салу есептерінің топтамасы ... ... ... ... ... ... .. ... ... ... ... ... ... ...

ҚОРЫТЫНДЫ ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ... ... ... ... ... ... . ... ... ... ... ... ... ...

ҚОСЫМША ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...

3

6

6
17
21
22
25
27
31
38
39

44

44
51

55

59

60

61

КІРІСПЕ

Мектеп геометрия курсында салу есептері үлкен мәнге ие. Өйткені олар геометрия курсында оқытылатын геометриялық образдардың арасындағы шынайы қатынастарды аңғаруға мүмкіндік береді. Сондай-ақ, салу есептерін шығару оқушылардың логикалық және белсенді ойлау қабілетін дамытады, кеңістіктік түсініктерін қалыптастырады. Шындығында, планиметрияда көмекші салуларды және күрделі логикалық ойқорытуларды қажет етпейтін көптеген есептеуге берілген есептер теоремалардың тұжырымдамасын, фигуралардың қасиеттерін және т.с.с. материалдарды бекітуге беріледі. Оқушылардың логикалық ойлауын дамыту және сол арқылы олардың білімдерін жүйелі, берік және терең ету үшін дәлелдеуге берілген есептер шығарылады.
Сондай-ақ, оқушылардың логикалық ойлауын дамытуда салу есептерінің де мәні үлкен. Бұндай есептерді шешуде талдау жасау, дәлеледеу және зерттеу оқушылардың бойында дұрыс ойлау және логикалық талқылау дағдыларын қалыптастыруға қажетті бай материал қорын ұсынады. Салу есептерін шығаруда оқушылар бір нақты фигурамен ғана жұмыс жүргізбей, элементтерінің әртүрлі жағдайында өзгерістерге ұшырап отыратын ізделінді фигураны құруы керек. Бұнымен біз оқушыларды ойлаудың диалектикалық әдісіне үйретеміз және мүмкіндігінше білімдегі формализмді жоямыз.
Төрт сатыдан тұратын салу есептерін шығарудың кезеңдері (талдау, салу, дәлелдеу, зерттеу) нақты ғылымдар саласындағы проблемаларды зерттеу және шешудің мықты құрылымы болып табылады. Бұндай есептерді шығару үдерісінде оқушылардың тиянақтылық, тыңғылықтық, шығармашылық сияқты қасиеттері дамиды.
Салу есептері оқытылған материалдарды бекітуге және қайталауға мүмкіндік береді, басқаша айтқанда олардың әрқайсысын шығару үшін геометрия курсының әртүрлі тарауларына қатысты білімдер қолданылады.
Салу есептерін шығару барысында геометрияның теориялық курсында қамтылмаған көптеген жаңа геометриялық фактілерді алуға (өзбетінше ашуға) болады. Мысалы, берілген элементтері бойынша үшбұрыштар салу есептерін шығару нәтижесінде үшбұрыштардың теңдік белгелерін өзбетінше тұжырымдай алады.Дипломдық жобада салу есептерін шығару барысында геометриялық есептердің басқа түрлерімен байланысын ғана емес, салу есептерінің басқа мектеп пәндерімен де (алгебра, физика, сызу) байланысын анықтайды.
Дегенмен мектеп геометрия курсында ең негізгі, ең қажетті деген салу есептері ғана беріледі. Оның өзінде сабақтарда ол есептер түгел шығарылмай, көпшілігі қалдырылып кетіп жататындығы жасырын емес. Оның негізгі себептерінің бірі, оқушыға салу есептерін шығару әдістерін үйретуден гөрі күрделі логикалық ойқорытуларды қажет етпейтін есептеуге берілген есептерді шығарып көрсету әлде қайда оңай болса, екінші жағынан мұғалімге көмек болатын салу есептерін шығаруға арналған әдістемелік әдебиеттердің аздығында (қазақ тілінде жоқтың қасы деуге болады) деп есептеймін.
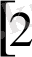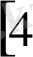Геометрия салу есептерін, оның ішінде Н.Г.О-ны есептерін шешудің теориясы мен практикасымен шұғылданған көптеген математиктердің еңбектері мен кітаптары жарық көрген. Олардың қатарына Рахымбек Д., Мадияров Н, Сейтжанова К.Б, . Рахымбек Д, Кенеш Ә.С, . Четверухин Н.Ф,.Стражевский А.А,.Мисюркеев И.В, 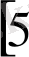. Александров И.И, 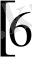. т.б көптеген авторлардың кітаптары мен мақалалары кіреді. Бұл кітаптар мен мақалалар нұктелердің геометриялық орны есептерін шешуді оқытуда мұғалімнің басты көмекші құралы болып табылады, яғни мұғалім бұл еңбектерден құнды мәліметтер таба алады. Мысалы: Стражевский А.А 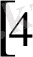кітабында, автор нүктелердің геометриялық орны есептерін шешудің методтарына, оқыту методикасына жан-жақты талдау жасаған Бұл еңбек- нүктелердің геометрияллық орны есептерін шешу туралы құнды еңбектердің бірі болып саналады.
Бұл дипломдық жобада нүктелердің геометриялық орындарын табу әдісін салу есептреін шешуге қолдану,мектеп геометрия оқулықтарындағы салу есептері және оны шығару әдістері, жазықтықтағы негізгі салу есептері, салу есептерін шығарудың негізгі кезеңдері оның ішінде әр есепке есептің шешілуі,талдауы, салу, оны дәлелдеу және зерттеу жұмыстары жеке-жеке көрсетілген. Планиметриялық салу есептерін шығарудың негізгі әдістері яғни: симметрия әдісі, түзулеу әдісі, қиылысу әдісі,ұқсастық және гомотетия әдісі, параллель көшіру әдісі,алгебралық әдістерінің әр бөліміне анықтама беріліп мысал есептерімен толықтырылған.Нүктелердің геометриялық орынына берілген салу есептері,жазықтықта ортақ қасиеті бар нүктелер жиыны,нүктенің геометриялықорны әдісін салу есептерін шығаруда қолдану жолдары, 7-9 сынып геометрия оқулықтарындағы н.г.о әдісімен шығарылатын салу есептерін шығару және н.г.о берілген салу есептерінің топтамасы көрсетілген.Осы жүйелерді қарастырып және зерттеп, қарастырып жатқан мәселелерді практикалық, яғни есептер мен сызбаларды қарастырамыз.
Тақырыптың өзектілігі: Нүктелердің геометриялық орны әдісі оқушылыардың кеңістіктегі елестетуін қалыптастырады, қалыптсатырудағы маңызы зор.
Жұмыстың мақсаты: Мектеп геометрия оқулықтарындағы салу есептері, жазықтықтағы негізгі салу есептері тақырыптар жайлы толық мағлұматтар және сол зерттелген мәселелерді оқушылардың түсінуі үшін берілген есептерді шығару және дәлелдеу;
Жұмыстың міндеті: а) геометриядағы нүктелердің геометриялық орны есептерін шығарудың теориясы мен практикасына арналған әдебиеттерге талдау; ә) мектеп геометрия курсындағы нүктелердің геометриялық орны есептерінің алатын орнын анықтау;
б) 7-9 кластардағы нүктелердің геометриялық орны есептерінің методикасы мен практикасына талдау жасау.
Жұмыстың зерттеу нысаны: Планиметриялық салу есептерінің шығарудың негізгі әдістеріне жеке-жеке түсіндірмелі талдау жүргізу.
Жұмыстың жаңалығы: қарастырылған тақырыптарды терең зерттей келе, тақырыпқа берілген есептерді шешудің жаңа жолдарын көрсету;
Жұмыстың практикалық маңыздылығы: Оқушыларды геометрия пәні бойынша алған теориялық білімін, дағдыларын қалыптастыру.
Диплом жұмысының кұрылымы: Бұл дипломдық жұмыс кіріспеден, екі тараудан және қорытынды, пайдаланылған дерек көздерінен тұрады.
1 тарау Мектеп геометрия оқулықтарындағы салу есептері және оны шығару
2 тарау Н.Г.О берілген салу есептерінен тұрады.

I. МЕКТЕП ГЕОМЕТРИЯ ОҚУЛЫКТАРЫНДАҒЫ САЛУ ЕСЕПТЕРІ ЖӘНЕ ОНЫ ШЫҒАРУ ӘДІСТЕРІ

1.1 Жазықтықтағы негізгі салу есептері
Геометриялық салу есебі - алдын ала берілген құралдарды пайдалана отырып, есеп шартын қанағаттандыратын фигураны салу
Салынған фигура салу есебінің шешімі делінеді.Кейде салу есебінің шартын қанағаттандыратын бірнеше фигура болуы мүмкін.Салу есебі шешілді делінеді,егер оның барлық шешімі табылса.
Есеп шартын қанағаттандыратын фигуралар бір бірінен тек жазықтықтағы орны арқылы ғана озгешеленсе есептің жалғыз ғана шешімі бар делінеді. Шешімі шексіз көп болатын салу есептер де болады. Ондай есептер есеп шарты жеткіліксіз берілген жағдайлардан туындайды.Ондай есептер шешілді делінеді,егер ол есепті шешудің жалпы жолы табылса.Мысалы, А және В екі нүктені басып өтетін шеңбер салу есебі осындай есепке жатады.Ізделінді шеңбердің центрі АВ кесіндісінің орта перпендикулярының кез келген нүктесі мен А нүктесінің ара қашықтығы болады.
Кейде есеп шартын канағаттандыратын фигура мүлдем болмауы, болған куннің озінде сайлап алынған құралдармен салынбауы мүмкін. Мысалы, концентрі шеңберлерге ортақ жанама мүлдем болмайды. Мұндай жағдайда, есеп шартын қанағаттандыратын фигураның жоқтығын дәлелдей алсақ есеп шешілді делінеді.
Кейде есепке шарт артық қойылуы себепті есептің шеуі болмауы мүмкін. Мысалы 4 нүктені басып өтетін шеңбер салу, екі қабырғасы мен екі бұрышы берілген үшбұрыш салу есептерінде шарт артық қойылған. Мұндай есептерді шарт артық қойылған есептер дейді.
Жалпы n-бұрышты бір мәнді салу үшін 2n-3 шарт орындалуы керек. Сонда үшбұрышты салу үшін 2n-3=2*3-3=3 шарт, төрт бұрышты салу ушін 2n-3=2*4-3=5 шарт берілуі керек..
Салу есептерін орындағанда есептің барлық мүмкін жағдайлары қарастырылады.Мысалы шеңберге А нүктеден жанама жүргіз десе, онда А нуктесінің шеңбер ішінде, шеңбер бойында, шеңберден тыс жататын жағдайларын жеке-жеке қарастыру қажет.
Салу есептерін шешу дегеніміз ол есепті төмендегі 1-5 пастулатта алынған қарапайым салуларға келтіру болып табылады.
П-1. Берілген екі нүктеден өтетін түзуді салу, яғни екі нүкте берілсе түзуді алынған деуге болады.
П-1 Берілген нүктені центр етіп, берілген екі нүкте арақашықтығын радиус етіп шенбер салу. Демек центрі мен радиусы берілсе шеңберді салынғаен деуге болады.
П-3. Параллель емес екі түзу түзудің қиылысу нүктесін салу. Демек берілген екі түзу параллель болса, олардың қиылысу нүктесі салынды деуге болады.
П-5. Берілген екі шенбердің қиылысу нүктесін салу. Бырақ күрделі салу есептеріндегі салудың әрбір қадамы 1-5 пастулатта баяндалған салуларға келтіру ұзаққа созылып кетеді. Көптеген күрделі салу есебінің шешілу құрамына кіретін қарапайым салу есептері болады.Ол есептер әдетте мектеп геометриясында қарастырылады. Егер салу есептерінің шығарылуы жолын бірнеше сатыларға бөліп, ол сатылар негізгі салуларға салынды деп есептеуге болады. Сондықтан салу есебін шешу - ол салудың 1-5 пастулаттарына және негізгі салу есептеріне келтіру болып табылады.
Жазықтықта салынған (яғни берлген) негізгі фигуралар (нүкте, түзу, шеңбер) жиыны Е-ны жаңа салынған негізгі (фигуралармен, нүктелер-мен,түзулермен,шеңберлерме н) толықтыру үшін түрлі салу құралдарын қолданылады. Ол құралдарға салу мүмкіндігін көрсететін түсініктемелер берілуі керек.Олар аксиома түрүнде беріледі.Салу құралдарына бір жақты және екі жақты сызғыштар,тік бұрыш, циркуль т.б жатады.
Ежелден қалыптасқан дәстүр бойынша салу құралы ретінде көбінесе сызғыш пен циркуль қабаттаса қолданылады.Сызғыш бір жақты,шкаласыз және шексіз деп есептеледі.Циркуль ашасыда шексіз деп есептеледі.
Демек циркуль мен сызғыш күнде қолданылып жүрген циркуль мен сызғыш емес, олар абстракцияланған болып табылады. Циркуль менсызғыш арқылы салынатын негізгі салу есептері қатарына мыналарды жатқызуға болады:
1. Берлеген сәулеге оның төбесінен бастап берілген кесіндіні өлшеп салу;
2. Берілген сәуледен берілген бір жарты жазықтықта берілген бұрышты салу;
3. Бұрыштың биссектрисасын жүргізу;
4. Берілген орта перпендикулярын жүргізу;
5. Кесіндінің ортасын салу;
6. Үш қабырғасы мен бойынша үшбұрыш салу;
7. Екі қабырғасы мен арасындағы бұрышы бойынша үшбұрыш салу;
8. Бір қабырғасы мен оған іргелес екі бұрышы бойынша үшбұрышсалу;
9. Берілген түзуге берілген нүктеден перпендикуляр түзу жүргізу;
10. Берілген нүктеден берілген нүктеге параллель түзу жүргізу;
11. Гипатенузасы мен бір сүйір бұрышы бойынша тік бұрышты үшбұрыш салу;
12.Гипатенузасы мен бір катет бойынша тік бұрышты үш бұрыш салу;
13. Шеңберге оның берілген нүктесінен жанама жүргізу;
14.Шеңберге берілген нүктеден жанама жүргізу.
Берілген сәулеге оның төбесінен бастап берілген кесіндіні өлшеп салу..
а түзуі және осы түзу бойынан А,Х,Z нүктелері алынған
Х және Y нүктелері А нүктелерінің бір жағында жататыны, Х және Z нүктелерінің де А нүктесінің бір жағында жататыны белгілі. Y және Z нуктелері А нүктесіне қатысты қалай орналасқан: бір жағында ма,әлде екі жағында ма?
Шешуі. А нуктесі арқылы өтетін а тузуінен өзгеше b түзуін жүргізелік. Бұл түзу жазықтықты екі жарты жазықтыққа бөледі.Осы жартыжазықтықтардың бірінде Х нүктесі жатады. Есеп шарты бойынша Х және Y,Х және Z нүктелері а тузуінде А нуктесінің бір жағында орналасқан, онда X Y Және XZ кесінділері b тузуімен қиылыспайды, яғни А нуктесі XY және XZ кесінділерінде жатпайды. Онда А нуктесі YZ кесіндісіне де тиісті емес ( YZ b тузуімен қиылыспайды),Y және Z нуктелері A нуктесінің бір жағында жатыр.
Т узудің берілген нуктесінен оның бір жағында орналасқан нуктелерінің жиынын сәуле немесе жарты түзу деп атайды.Бұл берілген нүктені сәуленің бастапқы нүтесі деп атайды. Тузудің әрбір нүктесі оны екі сәулеге бөлді және олардың бастапқы нүтелері ортақ .Тузудің осындай бастапқы нүктелері ортақ болып келген әр түрлі сәулелері бір бірінің толықтауыш сәулулері деп атайды.
Берілген сәуледен берілген бір жарты жазықтықта берілген бұрышты салу..
Бұрыш деп- бастапқы нүктелері ортақ болатын әр түрлі жарты түзулерден құралған фигураны айтады. Бұл ортақ нүкте бұрыштың төбесі деп ал жарты түзулер бұрыштың қабырғалары деп аталады.Егер бұрыш қабырғалары өзара толықтауыш сәулелер болса, онда мұндай бұрышты жазыңқы бұрыш деп атайды.Жазыңқы бұрыштың тең жартысы тік бүрыш деп аталады. Көбінесе тік бұрыштарды белгісімен көсетеді.
Төбесі О және қабырғалары а,b сәулелері болатын бұрыш бейнеленген.Бұрышты оның төбесін көрсету арқылы немесе оның қабырғаларын көрсету арқылы немесе оның уш нүктесі: төбесі және қабырғалары жататын екі нүктесі арқылы белгілейді.Бұрыш сөзін кейде
таңбасымен белгіленеді.
Кесінділерді өлшеп салу мен бұрыштарды өлшеп салудың негізгі қасиеттері мынадай: Кез келген сәуле бойынан оның бастапқы нүктесінен бастап ұзындығы берілген кесіндіні өлшеп салуға болады және бұл кесінді жалғыз болады.
Кез келген сәуледен берілген жарты жазықтықта градустық өлшем берілген бұрышты өлшеп салуға болады және бұл бұрыш жалғыз болады.
есеп. АВ сәулелесінде АВ кесіндісінен кіші АС кесіндісі өлшеп салынған. А,В,С нүктелерінің қайсысы қалған екеуінің арасында жатады?
Шешуі. В және С нүктелері бастапқы нүктесі А болатын сәуледе жататындықтан

1-сурет

Олар А нүктесімен бөлінбейді, яғни А нүктесі В және С нүктелері арасында жатпайды. В нүктесі А және В нүктелерінің арасында жатуы мүмкін бе? Егер В нуктесі А және С нуктелері арасында жатса, онда АВ+ВС=АС болуы қажет. Бұлай болуы мүмкін емес, өйткені есеп шарты бойынша АС кесіндісі АВ кесіндісінен кіші. Олай болса, В нуктесі А және С нуктесінің арасында жатуы мүмкін емес. Сондықтан С нуктесі ғана А және В нуктелерінің арасында жатады.
Берілген бұрышқа тең бұрыш салу..
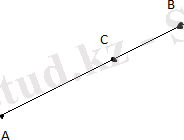
Шешуі. Ең алдымен есепті қалай түсүну керек екенін айқындап алайық, яғни не берілді және нені салу қажет екеніне жауап берейік. Төбесі О нүктесінде болатын (pq) бұрышы берілген. Онда циркульді және сызғышты пайдаланып, берілген (pq) бұрышына тең ВАС бұрышын салу қажет. Ол үшін О центрінен радиусы кез келген шеңбер жүргіземіз. Бұл шеңбердің p және q түзулерімен қиылысу нүктелерін сәйкесінше P және Q арқылы белгілейік. Бастапқы нүктесі А болатын кез келген а сәулесін алып, центрі А және радиусы РО ға тең шеңберді w(А;РО) арқылы белгілейік. Сонымен, В=аuw(А;РО).Енді келесі w(В;PQ) шеңберін жүргізейік (центрі В, радиусы PQ). w(А;РО) және w(В;PQ) шеңберінің қиылысу нүктелерін С арқылы белгілейміз. Онда BAC - бізге қажетті бұрыш.
2-сурет

Шынында да, ОРQ=ABC, өйткені салуымыз бойынша АВ=ОР,АС=ОQ, BC=PQ (3 белгі бойынша). Олай болса, POQ=BAC.
Бұрыштың биссектрисасын жүргізу
Бұрышты тең екі бөлікке оның ішкі сәулесін осы бұрыштың биссектрисасы деп атайды.

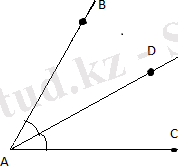
3-сурет

ВАС бұрышының АD ішкі сәулесі оны тең бөліктерге бөледі: BAD = DAC = BAC2, яғни AD сәулесі ВАС бұрышының биссектрисасы болады.
Мысал 2.Биссектрисаның бұрыш қабырғаларымен жасайтын бұрышының шамасы 90 С-тан аспайтынын көрсетейік.
Шешуі. Әрбір бұрыштың градустық өлшемі 180 С-тан артық емес. Сондықтан оның жартысы 90 С- тан артық болмайды.

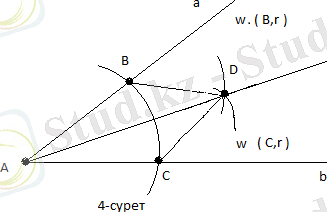
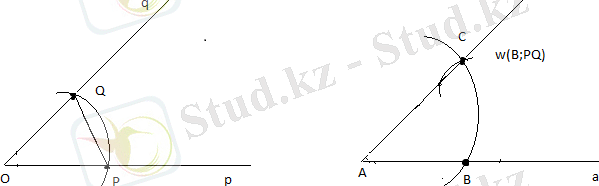
Есеп-3. Берілген бұрыштың биссектрисасын салу.

Шешуі. Төбесі А болатын (аb) бұрышы б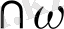ерілсін. 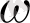(А;r) шеңберін жүргіземіз, r- кез келген оң сан. B=a 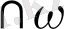(А;r) және С= b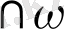(А;r) нүктелерін аламыз. Енді 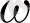(B;r) және 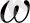(С;r) шеңберлерін жүргізіп,олардың қиылысу нүктесін D арқылы белгілейміз. Онда AD сәулесі (ab) бұрышының биссектрисасы болады. Бұл тұжырым ABD=ACD теңдігінен шығады.
Берілген кесіндінің орта перпендикулярын жүргізу
А,В,С үш нүктесі берілген.А және В нүктелерінен бірдей қашықтықта рналасқан және С нүктесінен берілген d қашықтығында орналасқан.
а) шартын қанағаттандыратын нүктелер жиыны АВ кесіндісінің орта перпендикуляры болад.
ә) шартын қанағаттандыратын нүктелер жиыны 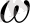(С;d) шеңбер болады.Онда бізге қажет нүкте осы шеібер мен АВ-ның орта перпендикулярын қиылысу нүктесі болады.
Салу. 1)АВ кесіндісінің орта перпендикуляры а түзуін жүргіземіз.
2) 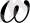(С;d) шеңберін жүргіземіз;
3) А түзуімен w(С;d ) шеңберінің Х қиылысу нүктесін анықтаймыз.

Табылған Х нүктесі бізге қажет нүкте.
Дәлелдеу. Салуымыз бойынша АХ=ВХ және СХ=d. Олай болса, табылған Х нүктесі есеп шартын қанағаттандырады.
Зерттеу. С нүктесінің а орта перпендикулярына дейінгі қашықтықта d1 арқылы белгілейік. Егер d1d болса, онда а түзуі мен w(С;d) шеңбері екі Х және Х1 нүктелерінде қиылысады,яғни есептің екі шешімі бар.
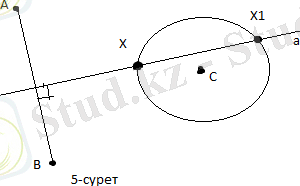
Кесіндіні қақ бөлу
Шешуі. АВ кесіндісі берілген. Кез келген r(rАВ2) радиуысын алып,w(А;r) және w(В;r) шеңберлерін жүргізе

Бұл шеңбер С және D нүктелерінде қиылысатын болсын. Онда О=АВ U CD нүктесі -АВ кесіндісінің ортасы: АО=ОВ. Шынында да АСD және BDC үшбұрыштары тең бүйірлі және өзара тең.( үш қабырғасы бойынша),Осыдан ACD=BCD теңдігі шығады, яғни СО-АСВ тең бүйірлі үшбұрышының биссектрисасы.Олай болса, СО осы үшбұрыштың медианасы да болады.Онда АО=ОВ.
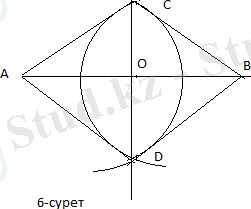
Үш қабырғасы бойынша үшбұрыш салу
Шешуі. P1Q1,P2Q2,P3Q3 кесінділері берілген. АВ=P1Q1, АС=P2Q2, BC=P3Q3 болатындай АВС үшбұрышын салу қажет.
а түзуінің бойынан АВ=P1Q1 кесіндісін өлшеп саламыз.w(A;P2Q2) және w(В;P3Q3) шеңберлерін жүргізіп, олардың қиылысу нүктесін С арқылы белгілейміз. Онда АВС бізге қажет үшбұрыш салынады.

Шынында да салуымыз бойынша АВ=P1Q1,АС=P2Q2, BC=P3Q3. Есептң екі шешуі бар. АВС1 де есеп шартын қанағаттандырады.Екінші жағынан, кез келген үш кесінді бойынша үшбұрыш салу әрқашан мүмкін бола бермейді.Үшбұрыш салынуы үшін берілген кесінділердің кез келгені қалған екеуінің қосындысынан кіші болуы қажет

Екі қабырғасы мен арасындағы бұрышы бойынша үшбұрыш салу
Шешуі.P1Q1,P2Q2 кесінділері мен (pq) бұрышы берілсін. Онда АВ=P1Q1,AC=P2Q2,A=(pq) болатындай АВС үшбұрышын салайық.
а түзуін салып ,циркульді пайдаланып, оның бойынан АВ=P1Q1 болатындай А және В нүктелерін аламыз.BAE=(pq) бұрышын саламыз.АЕ сәулесінен АС=P2Q2 болатындай С нүктесін аламыз. Онда АВС- бизге қажетті үшбұрыш.
Шынында да салуымыз бойынша АВ=P1Q1,AC=P2Q2 және BAC=(pq).

Үшбұрыштың бір қабырғасы, оған іргелес жатқан бір бұрышы және қалған екі қабырғасының қосындысы арқылы үшбұрыш салу
Берілгені: в,,а+с
Салу керек: АВС
Шешуі.Есепті шешілді деп есептейік. Ізделінді үшбұрыш болсын: АВ=с, ВС=а, АС=в,=

9-сурет
В нүктесінен бастап АВ қабырғасының созындысына ВМ=а кесіндісін саламыз. М және С нүктелерін қосамыз. үшбұрышы тең бүйірлі, себебі ВМ=ВС=а. вұл үшбұрыштың ВК медианасы оның биіктігі де болып табылады. Ал біз үшбұрышын екі қабырғасы в және а+с және олардың арасындағы бұрышы бойынша сала аламыз.
Салу. Берілген бұрышқа тең болатын бұрыш өлшеп салып оның төбесін А деп белгілейміз. Оның бір қабырғасына АС=в, ал екінші қабырғасына АМ=а+с - ларды өлшеп саламыз.М және С нүктелерін қосамыз. СМ кесіндісін қақ бөліп, К нүктесі арқылы СМ кесіндісіне АМ кесіндісін В нүктесінде қиятындай перпендикуляр тұрғызамыз. Пайда болған үшбұрышы ізделінді үшбұрыш болып табылады.
Дәлелдеу. және үшбұрыштарының теңдігінен (себебі салуымыз бойынша ВК-ортақ, СК=КМ, ВМ=ВС екендігі шығады.Бұл кесінділердің ұзындығын а деп белгілейік яғни ВМ=ВС= а. Онда АВ=АМ-ВМ=а+с-а=с. үшбұрышында АС=в,,АВ+ВС=а+с. Демек ізделінді үшбұрыш АВС үшбұрыш екен.
Зерттеу. а-с ва+с болған жағдайда есептің әруакытта біп шешімі болады, яғги АВС үшбұрышы біреу болады.
Берілген түзуге берілген нүктеден перпендикуляр түзу жүргізу
Берілген О нүктесі арқылы берілген а түзуіне перпендикуляр түзу жүргізу қажет.
Шешуі. Екі жағдай қарастырамыз: 1) О а; 2) О а.
1) О а болсын.Радиусы кез келген (О;r) шеңберін жүргізіп, оның а түзуімен қиылысуын А және В арқылы белгілейік 93-сурет. Радиустары r1,(r1r) бірдей (А;r1) және (В;r1) шеңберін жүргіземіз. Бұл шеңбердің қиылысу нүктесін С арқылы белгілейік.Онда ОС бізге қажет түзу,яғни ОС а. Шынында да, АОС= ВОС (үш қабырғасы бойынша), онда AOC=BOC=90

2) О а болсын.94-сурет. а түзуін А және В нүктелерінде қиятын (О;r) шеңберін жүргіземіз. Енді (А;r) және w(В;r) шеңбер85лері О және О1 нүктелерінде қиылысады.Онда ОО1 а.
Шынында да, АОВ=АО1В (үш қабырғасы бойынша). Онда ОАВ=О1АВ және үшбұрыштар теңдігінің белгісі бойынша АОС=АО1С. Мунда С=ОО1 а. Сондыктан ACO=ACO1=90

Беріген нүктеден берілген түзуге параллель түзу жүргізу
Ұзындығы d берілген а түзуіне параллель және ұштары k1 және k2 шеңберлері бойында жататын АВ кесіндісін салу керек.

11-сурет

Шешуі. Бірінші шеңбердің центрі арқылы берілген а түзуне параллель түзу жүргізіп, оның бойына ұзындығы d-ға тең О1 О2 кесіндісін саламыз.Центрі О1 нүктесі болатын берілген k1 шеңберіне тең k1 шеңберін жүргіземіз. Сонда k1 және k2 шеңберлерінің қиылысу нүктесі А іздеп отырған кесіндіміздің бір ұшынбереді. А нүктесі арқылы берілген а түзуіне параллель етіп жүргізілген түзу k1 шеңберін В нүктесінде қияды (ә-сурет) Табылған АВ кесіндісі есептің шартын қанағаттандыратыны көрініп тұр. K1және k2 шеңберлері үш жағдайда орналасулары мүмкін. Егер k1және k2 шеңберлері қиылыспаса,онда есептің нақты шешімі болмайды.Бұл екі шеңбер жанасса, онда есептің жалғыз шешімі болады. ә- суретте аталған шеңберлер екі нүктеде қиылысып тұр,оның екі шеңбері болады.
Гепатенузасы мен тік бұрышының төбесінен гепатенузага түсірілген биіктігі бойынша үшбұрыш салындар
Берілгені: с,hc
Салу керек: мұнда 90 Сондықтан есепті шешуді қысқаша келтірейік.
Шешуі: Диаметрі АВ=с болатын шеңбер салайық. Диаметрден h қашықтықта болатын және оған параллель а түзуін жүргізейік. Осы түзудің шеңбермен қиылысу нүктесі ізделінді тік бұрышты АВС үшбұрышының С төбесі болып табылады.
Берілген екі түзумен жанасатын және радиусы R-ға тең шеңбер салу керек
Шешуі. Берілген түзулерді а және в әріптерімен, ал іздеп отырған шеңберіміздің центрін О әрпімен белгілейік. Сонда О нүктесін а түзуіне параллель және одан R- ға тең қашықтықта орналасқан а1 түзуінің бойынан іздеуіміз керек. Сонда О нүктесін в түзуіне параллель және одан R-ға тең қашықтықта орналасқан в1 түзуінің бойынан іздеуіміз керек. Олай болса, О нүктесі а1 және в1 түзулерінің қиылысу нүктесі ретінде анықталады.

12-сурет
Салу. Берілген а түзуіне параллель және одан қашықтығы R-ға тең а1 түзуін саламыз. Ол үшін қалауымызша С нүктесін алып, осы С нүктесі арқылы а түзуіне перпендикуляр тұрғызылады. Тұрғызылған перпендикулярға R-ға тең кесіндісі салып, D нүктесін саламыз. (=R). Енді D нүктесі арқылы параллель а1 түзуін жүргіземіз. Берілген в түзуіне параллель және одан қашықтығы R-ға тең в1 түзуін саламыз. Салынған а1 және в1 тузулерінің қиылысу нүктелерінен, яғни О нүктесінен, берілген түзулерге перпендикуляр түсіріп А,В нүктелерән аламыз. Осыдан кейін центрі О нүктесі болатын және А және В нүктелері арқылы өтетін шеңберін саламыз.
Дәлелдеу. ә- суретте шеңбердің радиусы R-ға тең және ол а түзуімен А нүктесінде, ал в түзуімен В нүктесінде жанасады.
Зерттеу. Берілген түзуге параллель және одан берілген қашықтықта орналасатын және огымен бір жазықтықта жататын екі түзу жүргізуге болады. Олай болса, а түзуінен R-ға тең қашықтықтағы а1 және а2 параллель екі түзу в түзуінен R-ға тең қашықтықтағы в1 және в2 параллель екі тузумен төрт нүктеде қиылысады. Сондықтан берілген а және в түзулері қиылысатын болса, есептің төрт шешілуі болады. Егер ав және олардың ара қашықтығы 2R-ға теңболса (), онда есептің шексіз көп шешуі болады.Берілген түзулерден R-ға тең қашықтықта орналасқан және а және в түзулері жазықтығында жататын с түзуін жүргізуге болады. Сонда с түзуінің әрбір нүктесінде а және в түзулерімен жанасатын шеңбер сәйкес болады.Ондай шеңберлердің саны тең. Ал егер ав және олардың ара қашықтығы 2R - ға тең болмаса, онда есептің шешуі болмайды.

1.2 Салу есептерін шығарудың негізгі кезеңдері
Салу есебін шығару- салу есебінің шығару жолын анықтау;анықталған жол бойынша оны салу; салынған фигура берілген шарттарды қанағаттандыратынын дәлелдеу; есептің шешімі қандай жағдайларда болады, қандай жағдайда есептәі шешімі болмайды деген сұрақтарға жауап іздеуден тұрады.
Сонымен салу есебін шешу: талдау, салу, дәлелдеу, зерттеу кезеңдерінен тұрады. Әрине салу есебін шешуде бул схеманы арлық есепті де шығару үшін қатаң қолдану міндетті емес..
Бұл схеманың мәні төмендегідей:
1. Талдау кезеңі. Бұл кезеңде (талдау арқылы) есеп шартында берілген фигуралармен салынатын фигура арасындағы қатынастарды анықтайды.Ол үшін есеп шешілген деп ұйғарып, салынған фигураның жоба суреті алынады.Осы жоба суретте берілген фигуралармен салынған фигуралар арасындағы қатынасты талдай отырып, ізделінді фигураны салу қадамдарын белгілейді. Сөйтіп талдау кезеңі есепті шешу, фигураны салу жолдарын іздестіру нәтижесінде ізделінді фигураны салу қадамдарын тізбектей белгілеумен аяқталады.
2. Салу кезеңі. Бұл кезеңде талдау арқылы анықталған салу қадамдарын циркуль және сызғыш жәрдемімен бірінен соң бірі тізбектей орындалады. Сонда талдау кезінде салынған жоба сурет іздеген фигураның нағыз суретіне айналады.
3. Дәлелдеу кезеңі. Бұл кезеңде салынған фигураның есептің барлық шарттарын қанағаттандыратынын дәлелдейді.Сөйтіп салынған фигураны шынында да іздеп отырған фигура екеніне көз жеткізіледі.
4. Зерттеу кезеңі. Бұл кезеңде мына сұрақтарға жауап беріледі:
а) Таңдап алынған әдіспен есепті шешу әр уақытта мүмкін бе, яғни циркуль мен сызғыш көмегімен оны салуға болады ма?
б) Есептің қандай жағдайда шешімі бар және қанша, қандай жағдайда шешімі болмайды?
Міне осы сурақтарға жауап іздеу кезеңінің міндеті болып табылады.
Яғни зерттеу бөлімінің міндеті есептің шешілу шарттарын және шешім санын анықтау.Бұл кезеңде есептегі барлық мүмкін жағдайларын қарастыру үшін әр бір салу қадамдарын зерттеген жөн.
1-есеп. Бір қабырғасы және басқа екі қабырғаларына жүргізілген медианалары бойынша үшбұрыш салу
Шешуі. Есеп шарты бойынша салынатын үшбұрышқа тиісті үшбұрыш берілген, бір қабырғасы а, медианалары m1,m2.

13-сурет

Талдау. Есеп шешілген, яғни бір қабырғасы АС=а , медианалары АА1=m1, CC1=m2 болатын АВС салынған делік 121- а сурет АА1СС1=О дейік. Онда медиана қасиеті бойынша СО=2ОС1; АО=2ОА1 болу керек. Демек СО=23M2; АО=23M1; Ал ОС1=13M2, OA=13M1
Үшбұрыш өзінің үш төбесімен толық анықталады. Табаны АС=а салсақ А және С төбелер анықталады да, В төбесін салу ғана қалады. Ал, В=АС1СА1 болғандықтан, В нүктесін салу үшін С1 нүкте А1 нүктелерін салу керек. С1 нүкте СО, А1 нүкте АО сәулелерінде жатқандықтан А1 мен С1 ді салу үшін О нүктені салу керек. Егер О нүктесі салынса АО-ға АА1=m1, CO-ға СС1=m2 өлшеп салса В нүктесі табылады. Сонымен салу есебінің шешімі О нүктені табуға тіреледі. АОС-ны салсақ О нүкте салынады.
Салу. Талдауда анықталған салу қадамдарын еске ала отырып циркуль және сызғыш көмегімен мыналарды тізбектей саламыз.
1. Кез келген l түзуі бойына АС=а кесіндіні өлшеп саламыз.
2. Үш қабырғасы АС=а, АО=23m1, CO=23m2 бойынша АОС-саламыз.
3. АО,СО сәулелеріне АА1=m1, CC1=m2 кесінділерді өлшеп саламыз.
4. АС1,СА1 түзулерінің қиылысу нүктесі В-ны табамыз. Сонда шыққан АВС ізделінді үшбұрыш болады.
Дәлелдеу. Салу бойынша АС=а, АА1=АО+ОА1=23m1+13m1=m1; СС1=23m2+13m2=m2. Енді АА1 және СС1 кесінділері салынған АВС үшбұрышының медианасы екенін, яғни АА1=А1В және СС1=С1В болатындығын көрсетуіміз керек.Ол үшін А1С1 кесіндісінің АВС үшбұрышының орта сызығы екенін дәлелдеу жеткілікті. Егер D1 нүкте АО, Е1 нүкте СО кесінділерінің ортасы болса, D1,E1,A1,C1 төртбұрыш параллелограмм болады. б- сурет. Себебі OD1=OA1,OE1=OC1. Сондықтан А1С1= D1E1, A1C1D1E1 болады. D1E1 кесінді АОС- ның орта сызығы болғандықтан D1E1 AC және С1А1=D1E1=AC2 болады. Демек С1А1 кесінді АВС-ның орта сызығы болады. Сондықтан АА1,СС1 ол үшбұрыштың медианалары. Демек салынған АВС есеп шартын қанағаттандыратын, олай болса ол ізделінді үшбұрыш.
Зерттеу. Егер АОС салу мүмкін болса, АВС салу әруақытта бір мәнді орындалады. АОС салу 23 a 23 болған кезде ғана мүмкін.
Мұндай жағдайда есептің жалғыз шешімі болады.
23 a 23 есептің шешімі болмайды.
2- есеп. Екі қабырғасы және сол қабырғалардың біріне жүргізілген биіктігі арқылы үшбұрыш салындар
Бұл есепте әр түрлі үш кесіндісі берілген: а,b, h
Талдау. Есеп шешілген, ізделінді үшбұрыш салынған делік
Ол болсын а-сурет АС=b, BC=a, BD=h (биіктік) болсын.Егер b=АС өлшеп салынса А,С екі төбе анықталады.Сонда үшінші төбе табу ғана қалады.Ол төбе екі шартқа бағынады.1-ден оның С нүктеден қашықтығы а-ға тең болу керек, 2-ден АС түзуінен қашықтығы h- қа тең болуы керек.
Егер 2-шартты ескермесек В төбесі центрі С нүктесі, радиусы r=a болатын шеңберде жатуы керек.
Егер 1-шартты ескермесек В төбесі АС түзуінен h қашықтықта және оған параллель жүргізілген l түзуінде жатар еді.
Екі шартты да ескерсек В төбесі (С,а) шеңбері мен l түзуінің қиылысу нүктелерінің жиыны болуы керек.
Салу.Талдау кезеңінде анықталған есепті шешу (салу) қадамдарын циркуль сызғыш жәрдемімен мына тәртіпте орындаймыз. (б- сурет)

14- сурет

1. Кез келген d түзуі бойында АС=b кесіндіні өлшеп саламыз.
2. С центрлі а радиусты (С,а) шеңбер саламыз.
1) АС кесінді жатқан d түзуге перпендикуляр етіп m түзуін жүргізіп оның бойына d түзуден бастап h кесіндіні өлшеп саламыз. Ол EF болсын.
2) F нүктеден d түзуіне параллель етіп l түзуін жүргіземіз.
3) l мен (C,а) шеңбердің қиылысу нүктелері мен табамыз.
4) Ол нүктелерді А,С нүктелерге қосамыз АС, АС үшбұрыштар шығады.Олар іздеген үшбұрыштар болады.
Дәлелдеу. Бұл үшбұрыштарды салу бойынша АС=B,С=а, С=а себебі мен нүктелері (С,r=a) шеңберде жатыр. Салу бойынша l түзуінде жатыр. Сондықтан В1 мен В2 нүктелердің АС-дан қашықтығы, яғни АВ1С,АВ2С үшбұрыштың АС табанына жүргізілген биіктігі h-қа тең.
Сонымен салынған АВ1С, АВ2С үшбұрыштар есепте берілген үш талаптыда қанағаттандырады. Сондықтан олар ізделінді үшбұрыштар болады.
Зерттеу: 1,2- салулар әр уақытта бір мәнді орындалады.
3) Салу екі түрлі орындалуы мүмкін: h кесіндісі АС түзуінен үстіңгі және астыңғы жарты жазықтығында өлшеп салынуы мүмкін. Сондықтан EF1=h немесе EF2=h болып, F1, F2 нүкте табылады.
4) Салуы да екі түрлі: біреуі F1 екінші F2 нүктеден АС түзуіне параллель етіп жүргізілуі мүмкін.
5) Салу нәтижесінде АС-ның үстінгі жарты жазықтығында В1,В2, АС-ның төменгі жарты жазықтығында , нүктелер шығады және болады.
Бұл жағдайда l түзуі мен (С, r=a) шеңбер қиылысқан жағдайда ғана мүмкін. Олар қиылысу үшін ha болуы кеек. h=a болса l түзуі шеңберге жанасады. ha болса l түзуі шеңбермен қиылыспайды, яғни В нүктесі табылмайды.
Сөйтіп ha болғанда есептің екі шешуі болады. Олар . h=a болғанда l түзуі шеңбермен жанасады да B1=B2=B боолып бір ғана шығады.Сөйтіп бұл кезде есептің бір шешілу болады.
Егер ha болса есептің шешуі болмайды.

1.3 Планиметриялық салу есептерін шығарудың негізгі
әдістері

Бұл фигуралар планиметриялық негізгі ұғымдары: нүкте мен түзуі. Өлшемдері өте аз болатын нәрселерді, ты алыстан көрінетін заттарды (аспандағы жұлдыз т.с.с) қарастырсақ нүкте түсінігіне келеміз.
Керілген жіп, кітап парағының жиегі, түзудің бөлігі деген түсінікбере алады.Ал бүкіл түзу екі жаққа созылған деп есептеуіміз керек.
Нүктелерді латын алфавитінің үлкен А,В,С әріптерімен, ал түзулерді кіші а,в,с ... әріптерімен белгілейтін боламыз. Кітаптің парағы тынық көлдің немесе тақтаның бетін қарастырсақ, жзықтық ұғымына келеміз. Жазықтықтың жан-жақты шектеусіз созылатынын білуіміз керек. Жазықтықты грек әрпімен белгілейміз
Көптеген салу есептерін шешуге геометриялық түрлендіру әдістерін үлкен табыспен қолдануға болады.
Салу есебін шешу барысында берілген немесе ізделінді фигуралармен қатар оардан немесе олардың бөліктерінен қандайда бір түрлендіруді пайдалану нәтижесінде шыққан басқа фигураларды қарастыруға тура келеді. Оны салу оңайырақ болуы мүмкін. Ол фигураны салған соң оны кері түрлендіру арқылы ізделінетін фигура салынады. Түрлендірудің қандай түрі (қозғалыс, симметрия,параллель,көшіру, бұру,ұқсас түрлендіру т.б) қолданылғандығына байланысты салу әдісі де осылай аталады.
Планиметрия салу есептерін шығаррудың негеізгі әдістері орташа қиындықты және күрделі салу есебін шығару үшін арнайы әдістер пайдаланылады. Олар негізінен мыналар
- Симметрия әдісі
- Түзулеу әдісі
- Қиылысу әдісі
- Ұқсастық және гомотетия әдісі
- Параллель көшіру әдісі
- Алгебралық әдіс

1.3.1 Симметрия әдісі

Салу есебін шешуде, кейде ол есепті шешуде, кейде ол есепті берілген l, сызықпен басқа берілген l2 сызықты түрлендіруден шыққан l2 cызықтың қиылысу нүктесіне табуға келтіруге болады. Мұндай салу есептерін шешуге түрлендірудің симметриялы түрін пайдаланған ұтымды болады.
1 есеп. а,в,с үш түзуі берілсін. Бір диогоналы а түзуінде жататын және берілген m кесіндіге тең болатын, қалған 2 төбесінің бірі в, екіншісі с түзуінде жататын ромбы салу керек..

Талдау. Есеп шешілген, ромб салынған болсын:
АС=m,B. Сонда ромбыны салу оның тағы бір (мысалы D төбесін ) төбесін салуға беріліп тұр. Өйткені АС=m кесіндіні салу арқылы A,C төбелері салынды. Егер енді D төбе белгілі болса, онда АС-ға қарағанда D-ға симметриялы нүктені салса В табылады.
Егер В нүкте АС-ға қарағанда D нүктеге симметриялы болса, онда D нүкте в түзуге симметриялы в1 түзуде жатуы керек.Сондықтан ол с мен в түзулердің қиылысу нүктесі болады.
Салу: Төмендегі салуларды тізбектеу орындаймыз.
а) в түзуге а түзуге қарағанда симметриялы болатын в1 түзуді саламыз.
б) с және в1 түзулерінің қиылысу нүктесі D-ны табамыз.
в) D нүктеден а түзуіне перпендикуляр болатын DB түзуін жүргіземіз.
г) DB және в түзулердің қиылысу нүктесі В-ны табамыз.
д) DB мен а түзулердің қиылысу нүктесі О-ны табамыз.
е) О нүктеден а түзуіне ОА=m2, OC=m2 кесінділерін өлшеп салып А мен С нүктелерін саламыз.
Сонда ABCD ізделінді ромбы болады.
Дәлелдеу. Салу бойынша және АС мен в түзулер а түзуіне қарағанда симметриялы болғандықтан, Dжәне DBболғандықтан В мен D нүктелер симметриялы болады.Сондықтан ОВ=ОD және ВDболады.
Демек, ABCD ромб болады. (Диогоналдары бір-біріне перпендикуляр және олар бірін-бірі қақ бөледі) және есептің шартын қанағаттандырады.
Сондықтан ABCD ізделінді ромб болады.
Зерттеу: в-ға симметриялы в1 түзуі с түзуіне параллель болса есептің шешімі болмайды (D табылмайды.)
Түзулер в1=С (беттесе) есептін шексіз көп шешімі болады.в1 мен С түзулер а түзуден тыс нүктеде қиылысса есептің шешуі болмайды.
2-есеп. Берілген Ао,Во,Со нүктелері қабырғаларының қақ ортасы болатын үшбұрыш салындар (40- сурет)
Талдау. Есеп шешілген, ізделген үшбұрыш болсын.Одан оның төбелері Ао,Во,Со нүктелерге қарағанда сәйкесінше В және С,С мен А,А мен В симметриялы болады.
Сондықтан симметрия ұғымын пайдаланып, кез-келген D нүкте алып, Dco түзуінің бойына DCo=CoE, EBo түзуін жүргізіп оның бойына ЕВо=ВоF,FAo түзуінің бойына FAo=AoN кесінділерін өлшеп салсақ, DN кесінді өтеді және сол нүктеде қақ бөлінеді.Себебі симметрия ережесі бойынша DB=AE,DBAE; AE=FC, AEFC; FC=BN, FCBN Бұлардан DB=BN, DBBN.
Салу. а) D нүкте алып DCo түзуге DCo=CoE, Ebo түзуге EBo=DoF, Fao түзуге FAo=AoN нүктелерін салып D,N-ді қосамыз.
б) DN кесіндісінің ортасы В-ны табамыз.
в) ВСо түзуін жүргізіп, оның бойынан АВо=СоА болатын А нүтесін саламыз
г) АВо түзуін жүргізіп оның бойынан АВо=ВоС болатын С нүктесін саламыз.Сонда АВС іздеген үшбұрыш болады.
Дәлелдеу. Салу бойынша DB=AE=FC=BN,DBAEFCBN. Сондықтан СоDB= болады, бұдан АСо=СоВ. Осы сияқты бұдан АВо=ВоС; , бұдан ВАо=АоС.
Демек АоВоСо нүктелер АВС-ның қабырғаларының орталары. Сондықтан іздеген үшбұрыш болады.
Зерттеу. АоВоСо нүтелер бір түзудің бойында жатпаса есептің шешімі болады және ол біреу-ақ болады. Ал, ол нүктелер бір түзудің бойында жатса есептің шешімі болмайды.
3-есеп. а түзуінің бойынан берілген А және В нүктелерінен қашықтықтарының қосындылары ең аз болатын нүкте табу керек
Шешуі. Талдау. А және В нүктелері берілген а түзуінің бір жағында жатады ал М-іздеп отырған нүктеміз делік, яғни АN+BN-қосындысының мәні ең аз болады. а түзуіне қараңанда В нүктесі симмертриялы нүктесін салайық, сонда АN+BN=AN+ қосындысы ең аз болатындай етіп, табуға келіп тіреледі.Ал бұл А түзу кесінді болған жағдайда ғана болады.Өйткені а түзуәнде жатқан кез-келген басқа Ν˳ нүктесінен А және нүктелеріне дейінгі қашықтықтардың сол А және В′ нүктелеріне дейінгі қашықтықтарының қосындысынан үлкен болады(үшбұрыштың қабырғаларының қасиеті бойынш ANo+B′Ν˳AN+В′Ν) олай болса, ANo+B′NoAN+B′Ν

17-сурет

Cалу. А және В нүктелері берілген а түзуінің бір жағында жататын болсын. а түзуінің бойында В нүктесімен симметриялы В′ нүктесін саламыз. А және В′ нүктелері арқылы түзу жүргіземіз. Сонда а түзуі мен АВ түзуінің қиылысу N нүктесі іздеп отырғанымыз.
Дәлелдеу. Түзудің бойында жатқан М нүктесімен сәйкес келмейтін кез-келген Мо нүктесін алайық. Симметриялық қасиеті бойынша NB=NB′, сондықтан AN+BN=AN+NB′=AB′
AB′ANo+B′No болғандықтан,AN+BNANo+BNo.
Зерттеу. 1) Егер А және В нүктелері бірдей а түзуінің бойында жататын болса, онда есептің бір ғана шешімі болады.
Бұл жағдайда, егер А және В нүктелер а түзуінің екі жағында жатса, онда іздеп отырған нүктеміз Ν›АВ а болады. Егер бұл беріліп отырған екі нүктенің бірі а түзуінде жататын боса, онда іздеп отырған Ν нүктеміз сол ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.