Математикалық Тұжырымдамады қалыптастыру

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 59 бет
Таңдаулыға:

Ф.7.07-04

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

АКАДЕМИК Ә. ҚУАТБЕКОВ АТЫНДАҒЫ ХАЛЫҚТАР ДОСТЫҒЫ УНИВЕРСИТЕТІ

Тұнғыш Айгул Бақытжанқызы

ТАҚЫРЫБЫ: Мектепте математикалық Тұжырымдамадарды енгізудін технологиясы

ДИПЛОМДЫҚ ЖҰМЫС

5В010900 - Математика мамандығы

Шымкент, 2019 ж.

Ф.7.07-05

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

АКАДЕМИК Ә. ҚУАТБЕКОВ АТЫНДАҒЫ ХАЛЫҚТАР ДОСТЫҒЫ УНИВЕРСИТЕТІ

Информатика және математика кафедрасы

Қорғауға жіберілсін
__________кафедра меңгерушісі
ф.м.-ғ.к., профессор Юнусов А.А.
_______________2019ж.

ДИПЛОМ ЖҰМЫСЫ

ЖҰМСТЫҢ ТАҚЫРЫБЫ: Мектепте математикалық Тұжырымдамадарды енгізудін технологиясы
МАМАНДЫҒЫ 5В010900- МАТЕМАТИКА

Орындаған: Т109-15. Тұнғыш Айгул Бақытжанқызы

Дипломдық жұмыс жетекшісі: Профессор Юнусов А.А.

ШЫМКЕНТ-2019

Ф.7.07-06

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

АКАДЕМИК Ә. ҚУАТБЕКОВ АТЫНДАҒЫ ХАЛЫҚТАР ДОСТЫҒЫ УНИВЕРСИТЕТІ

Информатика және математика кафедрасы

Бекітемін
__________кафедра меңгерушісі
ф.м.-ғ.к., профессор Юнусов А.А.
_______________2018ж.

Дипломдық жобаны (жұмысты) орындауға арналған
ТАПСЫРМА

Студент Т109-15 Тұнғыш Айгул Бақытжанқызы

Жобаның (жұмыстың) тақырыбы Мектепте математикалық Тұжырымдамадарды енгізудін технологиясы
ЖОО № 20______ ж. бұйрығымен бекітілген
Аяқталған жумысты тапсыру
Тапсырманың берілген күні

Дипломдық жұмыс жетекшісі Профессор Юнусов А.А.

Тапсырманың орындауға алған студент Тұнғыш А.Б.
ШЫМКЕНТ-2019

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

АКАДЕМИК Ә. ҚУАТБЕКОВ АТЫНДАҒЫ ХАЛЫҚТАР ДОСТЫҒЫ УНИВЕРСИТЕТІ

Студенттің дипломдық жобасына (жұмысына)
ПІКІР
Сізге Университеттің_____________________ ________тобының студенті
___________________________________ _______________________жіберілді.
Пікірде келесі мәліметтерді көрсетуіңізді сұранамыз:
Тапсырманың орындалуының жан-жақтылығы, технико-экономикалық түсініктемесі, экономикалық есептеулер, конструктивтік шешімдері, сызулардың сапасы, еңбекті үйымдастыру.
Теориялық білімдердің деңгейі, оларды жұмыста пайдалану дәрежесі, өндірістің тәжірибелік жағдайларын есепке алу және шешімдердің нақтылығы.
Жұмысты зерттеудің тереңдігі мен ерекшелігінің негізгі белгілері.
Жұмысты рәсімдеудің сапасы мен жалпы сауаттылығы.
Сызу жұмыстарының сапасы.
Отандық және шет елдік әдебиеттерді қолдану деңгейі.
Жұмысты орындаудың жалпы бағасы.
Жауап беруді, түсіндіруді немесе диплом жазушының қорғауын талап ететін жұмыста кездескен қателіктерді ерекше көрсетуіңізді сұранамыз.
Пікірді "______" _______________ 20__ж күннен кешіктірмей беруіңізді және "______"________________20___ж күні болатын Мемлекеттік Аттестациялық Комиссияның отырысына қатысуыңызды сұраймыз.

Факультет деканы_____________________________ __"______" 20___ж.
Жобаның (жұмыстың) тақырыбы
___________________________________ ___________________________________ ___________________________________ ___________________________________ ___________________________________ _______________________
ПІКІРДІҢ МАЗМҰНЫ

Пікір берушінің аты жөні
Ғылыми атағы
Ғылыми дәрежесі
Жұмыс орны
Атқаратын қызметі
Қолы

Дипломдық жұмыс жетекшісінің пікірі

Студент

Жетекші ______ 20 ж.

Дипломдық жұмыс туралы кафедра қорытындысы

Дипломдық жұмыс кафедрада қаралды және

студент Мектепте математикалық Тұжырымдамадарды енгізудін технологиясы осы жұмысты

Мемлекеттік аттестациялау комиссиясында қорғауға жіберілуі мүмкін

Кафедра меңгерушісі 20 ж.

Мемлекеттік аттестациялау комиссиясының төрағасына №

АКАДЕМИК Ә. ҚУАТБЕКОВ АТЫНДАҒЫ ХАЛЫҚТАР ДОСТЫҒЫ УНИВЕРСИТЕТІ

факультетінің студенті Тұнғыш Айгул Бақытжанқызы

дипломдық жұмысты қорғауға жіберіледі

Жұмыс тақырыбы Мектепте математикалық Тұжырымдамадарды енгізудін технологиясы
Сынақ - емтихан ведомостілерінен көшірме, үлгерімі туралы анықтама, дипломдық жұмыс жетекшісінің пікірі, кафедраның дипломдық жұмысқа қорытындысы, дипломдық жұмысқа рецензия қоса жіберіледі.

Үлгерім туралы анықтама

Студент Тұнғыш Айгул Бақытжанқызы
Университетте 20 жылдан 20 жылға дейін болғанда мамандық бойынша оқу жоспарын келесі бағалармен орындады.
Өте жақсы %, жақсы % қанағаттанарлық %

Факультет деканы
Факультет хатшысы

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

АКАДЕМИК Ә. ҚУАТБЕКОВ АТЫНДАҒЫ ХАЛЫҚТАР ДОСТЫҒЫ УНИВЕРСИТЕТІ

Информатика және математика кафедрасы

Бекітемін
__________кафедра меңгерушісі
ф.м.-ғ.к., профессор Юнусов А.А.
_______________2019ж.

Дипломдық жобаны (жұмысты) орындауға арналған
ТАПСЫРМА
Студентке Тұнғыш Айгул Бақытжанқызы
Жобаның (жұмыстың) тақырыбы Мектепте математикалық Тұжырымдамадарды енгізудін технологиясы

ЖОО № 20______ ж. бұйрығымен бекітілген
Аяқталған дипломдық жумысты тапсыру мерзімі
Дипломдық жүмыстың негігі деректері
Диплом жобадағы әзірлеуге жататын сұрақтардың тізімі немесе дипломдық жұмыстын кысқаша мазмұны:
а) Функцияны оқытуға қажетті жалпы теориялық мәліметтер
б) Мектеп математика курсында элементар функцияларды оқыту технологиясы
Графикалық материалдың тізімі (міндетті дәл нұсқап)
Ұсынылған негізгі әдебиеттер_________________________ ___________________________________ ___________________________________ __________

Жобаға (жұмыска) қатысты тарауларды нұскап жоба (жұмыс) бойынша консультациялар

№
Рн
Тарау
Консультант
Мерзімдері
Қолы

Орындауды бастау
Ұсынулар

Дипломдық жобаны (жұмысты) әзірлеудің кестесі
№ Рн
Тараулардың аты, әзірленетін сұрақтар тізімі
Ғыылми жетекшіге
көрсету мерзімдері
Ескерту

Тапсырманың берілген күні 2018 ж.
Кафедра меңгерушісі
Жобаның (жумыстық) жетекшісі
Тапсырманы орындауға қабылдаған студент

Мазмұны.
Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...11
1.Математикалық Тұжырымдамады қалыптастырудың ғылыми-теориялық негіздері ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...15
2. Математикалық Тұжырымдамады қалыптастыру ... ... ... ... ... ... ... ... ... ... ... ... ... 27
2.1Математикалық Тұжырымдамадарды енгізудің әртүрлі тәсілдері ... ... ... ... ..42
2.2.Іс-әреттік қарым - қатынас ... ... ... ... ... ... ... ... ... ... ... ... ... .43
2.3. Зерттеушілік қарым - қатынас ... ... ... ... ... ... ... ... ... ... ... ... ..44
2.4. Тең бүйірлі трапеция Тұжырымдамаын енгізу.(8- сынып) ... ... ... ... ... ... ... 4 5
Қортынды ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...60
Пайдаланылған әдебиеттер тізімі ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..61

КІРІСПЕ
Оқыту - адамның бейімделуі мен актерлік дағдыларға, дағдыларға үйрету үшін негізгі құрал болып табылады. Оқу процесі нәтижесінде білім беру, тәрбиелеу және дамыту мақсаттары жүзеге асырылады.
Оқытудың мақсаты мен мазмұны, оны ұйымдастырудың түрлері мен әдістері, адамзаттың жалпы біліміне қойылатын талаптар өркениетті педагогикалық ұсыныстарға байланысты өзгеріп отырады. "Қалай тиімді оқуға болады?"Дәстүрлі педагогикадағы оқу үрдісін технологияландыру мәселесіне, сондай-ақ "неге оқуға болады?", "Как учиться?"Және" қалай оқуға болады?
Математикалық Тұжырымдаманың қалыптасу мәселесін, оның негізгі ерекшеліктері мен ерекшеліктерін анықтау. философтар в. В. Давыдов, Г. Е. Журавлев, Е. И. Психологтар сияқты Mashbits, SI Архангельский, Е. Б. Байдекбеков, Ж. А. Караев және басқа да. мұғалім жұмысы үшін. Қазіргі уақытта математикалық білім берудегі математикалық Тұжырымдаманың мәселелері С. Попертертер, Т. В. Габай, С. Уильямс, К. Маклин, Б. Хантер, И. В. Роберт еңбектерінде сипатталған.
Жалпы, О. П. Таркаев, А. В. Иващенко, В. Т. Конев, В. П. Пустовойтовтың зерттеулерінде математикалық Тұжырымдамадарды қолданудың педагогикалық аспектілері зерттеледі және оны қолданудың дидактикалық және педагогикалық шарттары анықталады. Психологиялық-педагогикалық негізі, оның әсерін оқушы қалыптастыру кезінде математикалық ұсыну болып табылады психологиялық-педагогикалық негізі Н. Ф. Талызина, Б. С. Гершинского, В. Н. Новикова, В. М. монахов, А. Я. Савелева, О. С. Тихомирова және басқа да. б. Есептеу техникасын қолдану әдістемесі-И. А. Катышев, Ю. И. Лобанов , Ю. А. Первин, А. А. Кузнецов, Ю. А. Шафрин және басқа да. ғалымдардың жұмыстары. Математикалық түсініктерді қалыптастырудың мәні, оқыту мазмұнының мәселелері. Я. Ваграменский, С. Гримм, В. М. Завыкин, А. П. Ершов, Г. Кочетков және басқа да. бұл ғалымдардың назарына жеткізілді. Мұндай жағдай елдегі жаңа ақпараттық парадигманың қалыптастырылуын айғақтауы мүмкін.
Математикадан орта мектептегі математикалық концепция мәселесін көптеген ғалымдар зерттеді, атап айтқанда М. С. Степанов, М. Вахидов, Б. Б. Бахедин, пәнаралық зерттеу Ю. А. Дробшев, жұмысты зерттеу - И. А. Дробсышева, "Алгебра және бастамаларды талдау" курсын оқу кезінде оқушылардың жеке белсенділігінің негіздерін қалыптастыру - Г. В. Ходякова, бастауыш мектепте математиканы оқыту - А. Ю. Байдыбекова, Иванов, жоғары мектепте математиканы оқытуда компьютерді пайдалану - Т. Аванесова, Н. а. Ю. Ғалым Аманжолов және басқа да ғалымдар еңбектерді зерттеді.
Жалпы білім беретін мектепте" Алгебра және бастамаларды талдау " Тұжырымдамаын оқыту мәселелері В. А. Гусев, А. Н. Е. Г. Глагавлева, В. А. Бахтина, А. Е. Әбілқасымова, Д. Рахимбек, Д. Ж. Икрамов және компьютерлік қосымшалар негізінде бірқатар теориялар мен оқыту әдістемелері бойынша "Алгебра және аналитикалық бастамалар" курсы (И. Дробсышева, Е. Е. Хвостенко, Т. Ж. Байдилдинов және т.б.). ) жұмыс істейді.
Мектептерде математикалық түсініктерді оқыту әдістемесін жетілдіру осы қарама-қайшылықты жою және дипломдық жұмыс тақырыбының өзектілігін анықтайды.
Дипломдық жұмыстың мақсаты: Математикалық тұжырымдаманы оқытудың әдістерін әзірлеу, оны қолданудың тиімділігін теориялық және тәжірибелік негіздеу.
Дипломдық жұмыстың құрылымы мен мазмұны. Дипломдық жұмыс кіріспеден, екі тараудан, қорытындыдан, пайдаланылған әдебиеттер тізімінен және қосымшалардан тұрады.
Кіріспеде Зерттеу тәсілі: өзектілігі, мақсаты, нысаны, пәні, міндеттері, зерттеу болжамы, зерттеу әдістері мен зерттеу кезеңдері, оның ішінде диссертацияның практикалық маңыздылығы, ғылыми жаңалығы мен қорғау үшін ұсынылған қорытындылар ұсынылған.
Зерттеудің бірінші тарауында информатика мен математикаға бағытталған мектептерді (сыныптарды) психологиялық-педагогикалық, оқу-әдістемелік әдебиет пен оқулықтарды талдау жолымен компьютерлік оқытудың теориялық мәселелері мен әдістері қарастырылады. Мұнда студенттердің санасында математикалық Тұжырымдамадар мен олардың қалыптасу мәселелері зерттеледі.
Екінші тарауда жалпы білім беретін мектептерде математикалық Тұжырымдамадарды қалыптастыру және зерделеу әдістері қарастырылады.
Қорытындыда зерттеу тақырыбы бойынша қорытынды тұжырымдар келтірілген.
Пайдаланылған әдебиеттер тізімінде зерттеу барысында талданған, қарастырылған психологиялық, педагогикалық, әдістемелік және арнайы әдебиеттер жинақталған.
Қосымшада зерттеу барысында пайдаланылған материалдар келтірілген.

1. Математикалық Тұжырымдамады қалыптастырудың ғылыми-теориялық негіздері
1. 1. Математикалық Тұжырымдамады қалыптастырудың мәні мен маңызы
Тұжырымдама-бұл нақты заттың немесе құбылыстың жалпы, маңызды және ерекше ерекшеліктері мен сипаттамаларын көрсететін ойлау түрі [1]. "Тұжырымдама - зерттелiнетiн объектiнiң жалпы, сонымен бiрге маңызды белгiлерi, негiзгi ой түйiнi болатын барлық айрықша сипаттары туралы түсiнiк, мәлiметтердiң тұтастай жиынтығы туралы пайымдар", - деп келтiрілген Әбілқасымова А., Д.Рахымбек және басқалардың еңбегiнде [2].
Педагогика ғылыми Тұжырымдамадарды олардың таным процесіндегі гносеологиялық және психологиялық маңызына сүйене отырып, білім мазмұнының басты құрылымдық бірлігі ретінде анықтайды. Оқушыларға ғылыми Тұжырымдамадарды игерту мәселесiн зерттеу Л.С.Выготскийдiң жетекшiлiгiмен басталды. Қазiргi кезде де Л.С.Выготскийдiң анықтаған Тұжырымдамады игеру процесiндегi оқушының ақыл-ой iс-әрекеттерiнiң өзгеру параметрлерiн пайдалану өзектi мәселе. Ол параметрлерге Тұжырымдама өлшемi, Тұжырымдаманың дерексiздендiрiлуі және оның қандай да бiр жүйеге ену дәрежелерi жатады. Бұл мәселелердi шешуге көптеген психолог ғалымдар: В.В.Давыдов, Е.Н.Кабанова-Меллер, Н.Ф.Талызина, Д.Н.Богоявленский, Н.А.Менчинская және т.б. [3] өз үлестерiн қосты.
Н.Ф.Талызина Тұжырымдама қалыптасу үшiн оқушы бiрiншiден, нақты облыстағы Тұжырымдамадардың қажеттi және жеткiлiктi белгiлерiн тағайындау операцияларын меңгеру, екiншiден, обьектiнi Тұжырымдамаға келтiру, обьектiнiң белгілі бір класқа тиiстiлiк салдарын шығарып алу және т.б. жалпылогикалық операциялар жүйесiн меңгеру керек деп анықтайды. Н.Ф.Талызина бойынша Тұжырымдамады қалыптастырудың психологиялық механизмiн осы операциялар жүйесi құрайды.
В.В.Давыдов "Мектеп математикасын оқытудағы негiзгi мақсаттардың бiрi оқушыларға Тұжырымдамады және бiлiмдi жалпылай алуды игерту болып табылады", - дейді.
Математикалық Тұжырымдамады игерудегi танымдық iс-әрекеттер құрылымына жалпы және пәннiң өзiне тән спецификалық ақыл-ой әрекеттерi кiредi.
А.И.Раев бойынша, жалпы ақыл-ой әрекеттерiне: талдау, жинақтау, салыстыру, дерексiздендiру және нақтылау, жалпылау және арнайыландыру, ұқсастықты тағайындау және қолдану, жiктеу және оларды жүйелеу жатады [4]. Бұлар жалпыланған Тұжырымдамадар мен пәндiк Тұжырымдамадар жүйесiн қалыптастырады, әрi нақты обьектiнiң қажеттi және жеткiлiктi белгiлерiн тағайындауды қамтамасыз етедi. Пәннiң өзiне тән спецификалық ақыл-ой әрекеттерiне Тұжырымдамаға келтiру әрекеттерi және керiсiнше, одан салдар шығару әрекеттерi жатады, яғни обьектiнiң Тұжырымдамаға қатыстылық дәйегiнен обьектiнiң қасиеттер жүйесiне өтемiз.
Кез келген Тұжырымдама, әсіресе математикалық Тұжырымдама табиғатта бар заттардың елеулі белгілерін абстракциялау арқылы пайда болады. Математиканың жаратылыстану ғылымдарынан ерекшелігі - оның Тұжырымдамадарының көп сатылы абстракциялау нәтижесінде пайда болатындығы [5].
Ж.Икрамов оқушылар математикалық Тұжырымдамадарды саналы игеруі үшін ойлау қызметінің логикалық-генетикалық құрылысын ашудың қажеттігін айта келіп, математикалық Тұжырымдама мен математикалық терминнің байланысын ашып көрсетеді [6].
Г.И.Саранцев орта мектепте математикалық Тұжырымдамадарды қалыптастыру мәселесiн зерттей келе, оның әдiстемесiнiң педагогика мен психологияның заңдылықтарын пайдаланып қана қоймайтынын, өзiндiк әдiстемелiк концепцияларының бар екендiгiн ашып көрсетедi [7].
Бiз, алдымен, Тұжырымдамады қалыптастыру процесiн сипаттайтын логикалық теорияларға сүйене отырып математиканы оқыту әдiстемесiнiң Г.И.Саранцев еңбектерiнде келтiрiлген 3 негiзгi концепциясына тоқталып, оны анализ бастамалары Тұжырымдамадарын қалыптастыруға пайдаландық.
I концепция. Тұжырымдамаға әкелу процесi - объектiнiң талап етiлген класын бiрмәндi анықтау үшiн жеткiлiктi болатын барлық қажеттi шарттарды iздеу түрiнде жүредi. Мысалы: "Туынды және оның қолданылуы" тақырыбындағы :
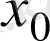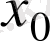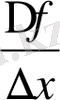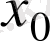" функциясы нүктесiнде үздiксiз болуы керек", " функциясының нүктесiнде туындысы бар болуы керек", "Δх--0 кезде -- f(х0)" - шарттарының әрқайсысы функциясының нүктесiндегi дифференциалын анықтаудың қажеттi шарты болып табылады. Оларды қос-қостан бiрiктiрсек те қажеттi шарт болып қалады. Тек барлық шарттарды бiрiктiрiп қарастырғанда ғана функцияның нүктедегi дифференциалын анықтаудың қажеттi және жеткiлiктi шарттары болып шығады. Тұжырымдамады анықтауда оған жақын Тұжырымдамадар жиi қолданылады. Мысалы функцияның дифференциалдануы Тұжырымдамаы шекке көшу, жанаманың бұрыштық коэффициентi Тұжырымдамадарымен туыстас болып келедi. Осылайша, логикалық тұрғыдан алғанда, Тұжырымдама мазмұны оның анықтамасымен теңестiрiледi.
II концепция. Тұжырымдама пiкiрлер жиынындағы "ақиқат" және "жалған" мәндердiң бiрiн қабылдайтын логикалық функция түрiнде қарастырылады. Тұжырымдама мазмұнының ашылуы оның қажеттi шарттарын iздеумен тiкелей байланысты. Бұл концепцияда Тұжырымдама мазмұнының бiрлiгi ретiнде жекеленген қажеттi шарт алынатындықтан, Тұжырымдама мазмұны оның анықтамасымен әр уақытта сәйкес келе бермейді.
III концепция. Тұжырымдаманың мазмұнын ашуда мазмұн бiрлiгiн қарастыру [76]. Мысалы функцияның дифференциалы Тұжырымдамаын қарастырайық. 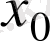нүктесiнде үздiксiз барлық функциялар жиынын H деп белгiлейiк.
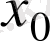а) шарты: " функциясының нүктесiнде туындысы бар"
b) шарты: "Δ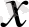--0 кезде 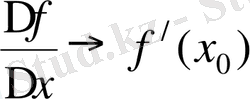" болсын.
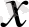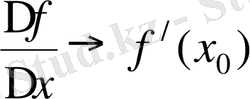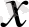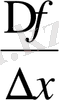
а) шарты H жиынын "үздiксiз, әрi туындысы бар" А класына және "үздiксiз, бірақ туындысы жоқ" Ā класына бөледi. H=A+ Ā. b) шарты А класын "үздiксiз, туындысы бар, Δ--0 кезде " B класына және "үздiксiз, туындысы бар, Δ--0 кезде 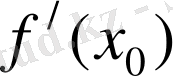мәнiне ұмтылмайды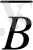" класына бөледi. A=B+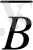. Функцияның дифференциалдануы Тұжырымдамаын игеру - ең алдымен барлық 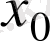нүктесiнде үздiксiз функциялардың iшiнен В, 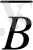кластарын құраушыларды тани бiлу және ажырата алуды талап етеді. Осы iс-әрекеттердi орындау процесiнде дифференциалданатын функция Тұжырымдамаы игерiледi, яғни, Тұжырымдаманың қасиеттерi анықталып, оның анықтамасы берiледi.
Мектептердегi 10-11 сыныптарда "Алгебра және анализ бастамалары" пәнi мұғалiмдерiнiң сабақ өтуiн, жұмысын қадағалау арқылы жоғарыда келтiрiлген концепциялардың бiрде-бiрi таза күйiнде мектептегi туындыға қатысты Тұжырымдамадарды игертуге келмейтiнiн байқадық. Бiрақ оның әрқайсысының элементтерi туындыға қатысты Тұжырымдама элементтерiн оқыту iс-тәжiрибесiнде қолданылуда. Мұндай жағдайда концепциялар мұғалiмге нақты жағдайда Тұжырымдамады қалыптастырудың қандай кезеңдерi болатынын, әрбiр кезеңге сәйкес қандай ақыл-ой iс-әрекеттерi орындалатынын түсiндiрiп бере алмайды.
Психолог ғалымдар бұл сұрақтарды зерттей келе, Тұжырымдамады игертуде келесi ақыл-ой iс-әрекеттерiн орындау қажеттілігін айқындайды: объектiнi Тұжырымдамаға келтiру, объектiнiң Тұжырымдамаға тиiстiлiгi фактiлерiнен салдарлар iздеу [8].
Мектепте анализ бастамаларын оқыту әдiстемесiнде ақыл-ой іс-әрекеттерiн игеру - Тұжырымдамады игеруге бағытталған тапсырмалар жүйесiн орындау, есептердi шығару арқылы жүзеге асатыны белгілі. Қазіргі қолданыстағы кейбiр оқулық авторлары бұл мәселеге онша көңiл бөлмеген. Мысалы, туындыға қатысты Тұжырымдамадарды қарастырайық. "Функцияның графигiне жүргiзiлген жанама" Тұжырымдамаын оқушыларға игерту тапсырмалары А.Н.Колмогоров және т.б. авторлардың оқулығында келтiрiлгенiмен, жанаманы сызуға бiр ғана есеп берiлген. Ал аргументтiң өсiмшесiн табу, функцияның өсiмшесiн табу есептерi көптеу берiлгенiмен, олардың берiлген функция графигi сызылған координаталық жазықтықтағы орнын көрсетiп беру есептерi тiптi берiлмеген.
Анализ бастамаларының тапсырмалар жүйесiне қойылатын талаптары мәселесiмен көптеген ғалымдар (П.М.Эрдниев, Ю.М.Колягин, В.В.Гузеев, В.А.Онищук, А.Ф.Эсаулов және т.б.) айналысқан. Тапсырмалар жүйесiне қойылатын талаптардың негiзгiсi - оның толықтылығы. Әдіскер ғалымдар тапсырмалар жүйесiнiң толықтығын әртүрлiлiгi позициядан қарастырады. Мысалы, П.М.Эрдниев дидактикалық бірліктерді ірілендіру концепциясы негізінде, В.В.Гузеев тақырыпқа байланысты тапсырмалар жүйесінің жан-жақты болуы керектігіне тоқталған.
А.Н.Иванов және Ю.Ф.Фомин тарауға арналған тапсырмалар базасын, сондай-ақ аралық және қорытынды бақылау жұмыстары базасын құруды ұсынады.
Жалпы оқытудағы тапсырмалар жүйесiне қатысты көзқарастар әртүрлi болғанымен, олардың толықтық принципiне қойылатын талаптары бiрдей болып келедi. Олар:
- тапсырмалардың математикалық мазмұнына қойылатын талаптар;
- тапсырмалар жүйесiн оқу процесiн ұйымдастыру тәсiлi түрiнде қарастырудан шығатын талаптар.
Жаратылыстану-математикалық бағдарлы мектептерде туындыны оқытуға арналған, соның iшiндегi функцияның экстремумына арналған тапсырмалар жүйесi дәстүрлi қолданыстағы оқулықтарда және есептер жинақтарында Тұжырымдамады қалыптастыруға қажеттi және жеткiлiктi болатындай толық еместiгiн байқауға болады.
Экстремум Тұжырымдамаы бiрiншiден өзiне екi кванторды бiрiктiредi, екiншiден оны оқытудағы алгоримтдiк жүйе барлық функциялар үшiн бiрдей емес. Сондықтан оқушылар оқулықтардағы және есептер жинақтарындағы берілген тапсырмаларда көбiне нүктеде экстремум болатынын не болмайтынын дәлелдейдi. Шындығында бұл Тұжырымдамады игеру үшiн оқушылар өте көп, әртүрлi тапсырмаларды орындаулары қажет. Бiз Н.Я.Виленкин және т.б. [9], Н.Темиргалиев және т.б. [10] , А.Н.Колмогоров және т.б. [11] оқулықтарындағы осы тақырыпқа байланысты тапсырмалар жиынтықтарының саны мен түрлерiн қарастырып, талдап шықтық. Бұларды таңдау себебіміз: [12] - Қазақстан Республикасы Білім және ғылым министрлігі жалпы орта білім беретін мектептеріне бекіткен; [13] - Ресей Федерациясының Оқу министрлігі жаратылыстану бағдарлы мектептеріне бекіткен; [14] - еліміздің орта мектептеріне арналған оқулығы болып табылады. 1-кестеде аталған оқулықтардағы функцияның қасиеттерiне байланысты берілген тапсырмалар саны келтiрiліп отыр.

Кесте 1 - Функцияның қасиетіне байланысты оқулықтарда берілген тапсырмалар саны

Функцияның қасиетi
Оқулық

[9]
[10]
[11]
Экстремум нүктесiнде диференциалданбайтын функциялар

5

1

7
Экстремум нүктесiнде үзiлiстi функциялар
-
-
-
Экстремум нүктесiнiң маңайында монотонды емес функциялар
-
-
-

1- кестеден функцияның экстремум нүктесiндегi қасиетiне келтiрiлетiн тапсырмалар санының аздығын бiрден байқауға болады.
Функцияны зерттеудi оқып-үйренуде өте жиi қолданылатын тапсырмалар - функцияны экстремумға зерттеу болып табылады. 2-кестеде жоғарыда келтiрiлген оқулықтардағы осындай тапсырмалар саны функциялардың түрлерiне байланысты келтiрiлген.
Қарастырылған мектеп оқулықтарында қарапайым рационал (сызықты және квадрат теңдеулер), бөлшек рационал теңдеулердi шешу тапсырмалары жеткiлiктi келтiрiлетiндігін, басқа теңдеу түрлерi 1-3 данадан ғана берiлетiнiн байқаймыз.
Н.Я.Виленкин және т.б. оқулығында тригонометриялық функциялар көптеу қарастырылғанымен, модульге қатысты есеп тіпті берілмеген екен. Және де экстремум Тұжырымдамаын оқып-үйренуге байланысты тапсырмаларды талдау объектiнiң Тұжырымдамаға қатыстылығын анықтайтындай қосымша шарттармен толықтыру, экстремум мәнi, түрi берiлген жағдайда функцияның графигін сызу, жалпылау есептерi берiлмегендiгiн байқадық. Сондай-ақ, оқушылардың экстремумды iздеуде орындайтын ақыл-ой iс-әрекеттерiнiң барлық тапсырмалар үшiн бiрдей екендiгiне көз жеткiздiк.
Бұл талдаулардан функцияны зерттеуге қатысты, жалпы анализ бастамалары Тұжырымдамадарына қатысты тапсырмалар жүйесін әлі де толықтыру мәселесін қолға алуды талап ететіні шығады. Өйткені, оқушылар берiлген Тұжырымдамаға тиiстi объектiлердi құра алғанымен, объектiнi тануға арналған тапсырмалардың аз берiлуiнен Тұжырымдамаға келтiру орындалмайды.

Кесте 2 - Функцияның түріне байланысты оқулықтарда берілген тапсырмалар саны

Функцияның түрi
Оқулық

[А]
[Ә]
[Б]
Рационал
8
3
7
Бөлшек рационал
4
2
4
Иррационал
6
-
3
Модуль таңбасымен берiлген
-
2
2
Тригонометриялық
10
1
-
Көрсеткiштiк
-
3
-
Логарифмдiк
-
3
-
Транценденттiк
1
-
-
Параметрмен берiлген
-
-
-

Логикалық тұрғыдан алсақ, анықтама ретiнде Тұжырымдаманың қажеттi және жеткiлiктi қасиеттерiнiң әртүрлi жүйелерi қабылдануы да мүмкiн. Сондықтан тапсырмалар жүйесінде берiлген Тұжырымдамамен жүргiзiлетiн әртүрлi математикалық iс-әрекеттер қамтылуы тиiс. Олар: объектiнi құрастыру; объектінің Тұжырымдама көлемiне тиiстiлiгiн анықтау; объектiнiң қасиеттерін ашу, оның Тұжырымдамаға қатыстылығын анықтайтындай қосымша шарттармен толықтырылуы; есептер шығаруда берiлген Тұжырымдамаға сүйену т.с.с.
Функцияның экстремумы Тұжырымдамаымен жұмыс тәсiлдерiнiң бiрнешеуiн көрсетейiк:
- берiлген нүктенiң функцияның экстремум нүктесi болатындығын дәлелдеу;
- функцияны экстремумға зерттеу, егер экстремум бар болса, оны сипаттау;
- экстремум түрi мен мәнi бойынша функцияның графигін сызу;
- экстремум Тұжырымдамаын есептердi шығаруды қолдану және т.б.
Сонымен, оқушылар анализ бастамалары Тұжырымдамадарын тиімді игеру бағытындағы ақыл-ой іс-әрекеттерін орындау үшін оқыту әдiстемесінде Тұжырымдама мазмұнын толық қамтитындай тапсырмалар жүйесін құрастыру және таңдау мәселесiн шешу тұр.
Г.И.Саранцев, М.В.Волович және т.б. ғалымдардың еңбектерiнде Тұжырымдамады қалыптастыру кезеңдерi және кезеңге сәйкес орындалатын тапсырмалар түрi берiлген (3-кесте), [15].
Тұжырымдамады қалыптастырудың алғашқы кезеңi - мотивизация кезеңi болып табылады. Бұл кезеңде қарастырылатын Тұжырымдаманың маңызын көрсету, оны оқып-үйренуге оқушының қызығушылығын тудыру мақсаттары жүзеге асады.
Мотивация оқушыларға математикалық емес мазмұндағы есептердi шығару арқылы, сондай-ақ математикалық теорияны дамыту қажеттiлiгiн түсiндiретiн арнайы тапсырмаларды орындату барысында жүзеге асады. Мысалы: Түзу мен үздiксiз жатық қисықтың қандай да бір аралықта өзара орналасуын қарастыруда мынадай үш түрлi жағдай болуы мүмкiн:
1) түзу мен жатық қисық қилыспайды;
2) түзу мен жатық қисықтың екi не одан да көп ортақ нүктелерi болады;
3) түзу мен жатық қисықтың бiр ғана ортақ нүктесi болады.
Оқушылардан жанама дегенді қалай түсінетінін сұрасақ, олардың көбі түзу мен жатық қисықтың бiр ғана ортақ нүктесi болса, ол түзу берiлген нүктеде жүргiзiлген жанама деген пікір айтады. Бұл пікірдің үнемі дұрыс бола бермейтінін мысалдармен келтірейік:
1-мысал. =1 түзуі мен y=2 параболасының М(1;1) нүктесі ортақ болғанымен =1 түзуі параболаның жанамасы емес, ал сол нүктеден өтетін y=2-1 түзуі жанама болады.
2-мысал. =0 түзуі мен y=cos графигін алсақ, олардың ортақ К(0;1) нүктесі бола тұра, ол түзу қисыққа жүргізілген жанама болмай, y=1 түзуі жанама екендігін және (2k;1), мұндағы kZ нүктелердің әрқайсысында жанасатынын келтіруге болады.
Мотивизация кезеңi үшiн көрнекiлiктi қолданудың орны ерекше. Мысалы, "Туынды және оның қолданылуы" тарауындағы функцияның үздiксiздiгi Тұжырымдамаын енгiзуде алдымен интуитивті-иллюстративті тәсіл қолданылады. Қарапайым функциялардың графиктерiн (y=k+b, y=2; y=; y=sin; y=cos) сызып көрсетудi қаламды қағаздан алмастан үздiксiз қозғалыс арқылы орындауға болады.
Оқушыларға көрнекi түрде осы iс-әрекеттердiң орындалуын көрсету керек және y=2 функциясының графигiн дәптерге үздiксiз қозғалыспен сыздырып, y=2 функцияның үздiксiздiгi туралы айтуға болады. Жалпы жағдайды да осыған ұқсас түрде қарастырамыз:
Егер y=() функциясының графигiн I аралығында қаламды қағаздан көтерместен сызуға болатын болса, онда функциясы осы I аралығында үздiксiз. y= функциясын қарастырсақ, бұл функция (0;+) аралығында және (-; 0) аралығында үздiксiз. Бұл функцияның графигiнiң (0;+) аралығында сызылуын жеке және (-,0) аралығында сызылуын жеке көрсету керек. Осыдан кейiн оқушыларға y= функциясының сан осiнiң 0-ден басқа әрбiр нүктесiнде үздiксiз екендiгi туралы айтылады. y=tg функциясының графигiн сызуды осы жолмен көрсету арқылы, оның () аралығында және сондай-ақ, кез келген үшiн аралықтарында да үздiксiз екендiгi айтылады, яғни y=tgx функциясы нүктесiнен өзге нүктелердiң бәрiнде үздiксiз функция болып табылады.

Кесте 3 - Тұжырымдамады қалыптастыру кезеңдерi және тапсырмалары

Тұжырымдамады қалыптастыру кезеңдерi
Оларды жүзеге асыратын тапсырмалар

Тұжырымдамады енгiзу мотивациясы
Оқып-үйренген Тұжырымдамадар мен теоремаларды
ашуға арналған тапсырмалар.
Тұжырымдамадарға келтірілетін іс-тәжiрибелiк сипаттағы
тапсырмалар.
Тұжырымдаманың ма-ңызды қасиетте-рiн ерекшелеу
Көрсетiлген қасиеттерге ие объектiлердi құруға
арналған тапсырмалар.

Тұжырымдаманың анықтамасы - ның логикалық құры - лы - - мын игеру
Фигуралардың моделдерiмен жұмыс iстеуге
арналған тапсырмалар.

Тұжырымдаманың көлемiне тиiстi объектiлердi танып
бiлуге арналған тапсырмалар.

Тұжырымдаманың анықтамасынан шығатын салдарларды
ерекшелеуге арналған тапсырмалар.

Шарттарды толықтыруға арналған Тұжырымдамады
танып- бiлу есептерi және салдарлар шығару
тапсырмалары.
Тұжырымдамады қолдану
Тұжырымдамаға байланысты тапсырмаларды
құрастыру
Оқып үйренiлетiн Тұжырымдаманың басқа да Тұжырымдамадармен байланы - сын тағайындау
Әртүрлi жағдайға Тұжырымдамады қолдану
тапсырмалары.

Тұжырымдамады жүйелеуге арналған тапсырмалар.

Математикада қандай да бiр нақты есептi шығару нәтижесiнде пайда болған теория кейiннен математиканың iшкi заңдылықтарына бағынып дами беретiн жағдайлар жиi кездеседi. Сондай мысал ретiнде туынды Тұжырымдамаын келтiруге болады. Жанаманың бұрыштық коэффициентiн табу және дифференциалданатын () функциясының өзгеру жылдамдығын табу есебiнен математиктер = болғандағы () функциясының туындысының мәнiн анықтау негiзiнде өрнегiн алған (5-сурет).

y
N

M

Сурет 5 - Қисыққа М нүктесiнде жүргiзiлген жанама

() функциясының графигiне нүктесiнде жүргiзiлген жанаманың бұрыштық коэффициентi (x0) - туындының геометриялық мағынасы деп, ал () функциясының = нүктесiндегi лездiк жылдамдығы () - туындының физикалық мағынасы деп аталады.
"Дифференциалдау" Тұжырымдамаын аналитикалық түрде түсiндiрудi алдымен 2-2; 3-3; өрнектерiн көбейткiштерге жiктеу мысалынан бастайды [83]:
а) 2-2=(-)(+);
б) 3-3=(-)( 2++2); (1)
в)
Келтiрiлген өрнектердiң бәрiнде (-) көбейткiшi бар, яғни теңдеудiң сол жағы (-)-ға тура пропорционал, нүктесiнде үздiксiз функция болып табылады.
Егер нүктесiнiң маңайындағы барлық үшiн
()-()=(-)g() (2)
болса және () функциясы нүктесiнде үздiксiз болса, онда функциясы нүктесiнде дифференциалданады.
() санын функциясының нүктесiндегi туындысы деп атайды және оны () деп белгiлейдi.
(1) теңдiктегi
а) ()= 2 функциясы үшiн ()=(+)-ға тең және нүктесiнде үздiксiздiгiнен ()=2 функциясының нүктесiнде дифференциалданаты-ны шығады және ()= ()=+=2. Ќысқаша, кез келген үшiн ()=2 түрiнде жазылады.
б) ()=3 функциясы үшiн ()=2++2 болады және ол нүктесiнде үздiксiз, сондықтан да ()=3 функциясы нүктесiнде дифференциалданады.
()= ()=32; - кез келген нүкте болғандықтан,
()=( 3)=32;
в) ()=, мұндағы 0, 0, функциясы үшiн ()= (0, 0,) нүктесiнде үздiксiз. Бұдан ()= функциясы нүктесiнде дифференциалданатындығы шығады. теңдiгінен = белгiлi бiр дәлдiкпен алынғанда кез келген ()= ()=().

2.Математикалық Тұжырымдамадарды енгізу әдістемесі
2.1Математикалық Тұжырымдамады қалыптастыру
Тұжырымдаманы әзірлеу-тұжырымдаманың мазмұнын, оның мазмұнының көлемін, басқа тұжырымдамалар мен дәлелдердің маңыздылығын қамтиды. Осылайша, бағдарлаудың табиғи-математикалық мектептерінде туынды және қосымшаларда тұжырымдамалық тұжырымдамаларды әзірлеуге арналған есептер жүйесі тұжырымдамалық негіз (Тұжырымдаманың мазмұны) және тұжырымдаманың барлық маңызды белгілерін ашатын ұқсас есептерден (Тұжырымдаманың әрекет ету саласы) тұруы тиіс.
Талдау арқылы оқушы субъектінің тұлғасын анықтайды және керісінше, затты жалпы белгілермен біріктіреді. Нәтижесінде объектінің маңызды жалпы қасиеттері ажыратылмайды және терминмен белгіленеді. Процесс жалпыланған тұжырымдамамен аяқталады. Ол өзінің бірегей ерекшеліктері бар, өйткені барлық тұжырымдамаға қолданылады. Егер тұжырымдама формальды болса, ол анықтама ретінде тұжырымдалады. Дегенмен, тұжырымдама да ұсынылады.
Жалпылау процесі дезагрегацияны қамтиды, өйткені объектілерді бір сыныпқа біріктірген кезде оның елеулі белгілерін ескермей ғана елеулі белгілерді атап көрсету керек.
Бұл әрекеттер оқушыларға арнайы оқыту контекстінде жалпы психикалық мінез-құлықтың негіздерін және іс-әрекеттің бір бөлігі болып табылатын келесі әрекеттерді ұсынуы тиіс:
1. Кірістірілген Тұжырымдаманың негізгі ерекшеліктеріне назар аударыңыз.
2. Объектінің маңызды және маңызды емес ерекшеліктерін табу.
Осылайша, Г. Саранцев, М. Б. Волович қарастырған тұжырымдаманы қалыптастыру процесінде зияткерлік қызметтің екінші кезеңі өткізіледі және екінші кезеңнің нәтижесінде Тұжырымдаманың анықтамасы беріледі.
Тұжырымдаманың тұжырымдамалық анықтамасы студенттердің санасында Тұжырымдаманың қалыптасуымен аяқталмайды. Тұжырымдаманы қалыптастыру оны студенттердің маңызды қасиеттерін анықтауға, олардың арасындағы байланысты көрсетуге, түрлі жағдайларда тұжырымдаманы қолдануға, әртүрлі табиғаттағы жаттығуларды орындауға және басқа пәндерде қолдануға қабілеттілігімен түсіндіруге болады. сондықтан Тұжырымдаманың логикалық құрылымы үшінші кезеңде әзірленетін болады.
Тұжырымдаманың логикалық құрылымына негізінен 3-кестеде берілген жүйелік контентті ашатын міндеттерді орындау жолымен қол жеткізіледі.
Төртінші кезең-нақты жағдайды қолдану тұжырымдамасы. Бұл кез келген пәнді зерделеудегі, әсіресе талдау материалдарын жүйелендіру процесіндегі маңызды қадам.
Тұжырымдаманы әзірлеу кезінде студенттерге "ми жуу" теориясын қалай қолдана аламыз?
П. Я. Гальпериннің ақыл-ой қызметі жарақаттану теориясына негізделген, тек операция кезінде, әрекет ету тәсілі іздестірудің параллель өрісімен қамтамасыз етілген жағдайда. Сондықтан әрекет тәсілдерін әзірлеу міндеті:
- әрекет негіздері;
- операциялар операцияларының негізгі операцияларының бөліктерінен тұруы тиіс.
П. Гальпериннің теориясына сәйкес, пәннің кез келген қызметі басшылықтан, жүзеге асыру мен бақылаудан, бақылаудан тұрады. Әрекет сапасы бағдарға байланысты. Сондықтан біліктілікті қалыптастыру процесті басқару механизмі болып табылатын басқарушы қағидаттарды әзірлеуден басталады.
Іс жүзінде, оқыту барысында оқушы " сынамалық қате "әдісін жиі қолданады. Мұндай іздеу оқу мақсатына жету нәтижесінде орындалса да, әзірленген материал оқу ортасындағы өзгерістерге байланысты тұрақсыз және жаңа жағдайға көшіру кезінде тиімсіз.
Және басқару принциптері, соның ішінде әрекет үлгілері, сондай-ақ жаңа әрекетті қалай орындау туралы нұсқауларды қамтиды. Бұл жағдайда оқу процесі тез жүріп жатыр. Оқушылардың білімі тұрақты негізде қалыптасады және оларды пайдалану кезінде айтарлықтай тиімділікке қол жеткізіледі. Маршруттау негіздерінің ерекшелігі Қызметтің дұрыс қалыптасуымен, даму жағдайларымен және мазмұнда бағдарлармен анықталады. Іс-әрекеттің негізі студенттің өзі болып табылады, бұл ретте нәтижеге осы тапсырмаға сәйкес қол жеткізіледі [16].
Ақылға қонымды негіз-бұл ажырамас бірлік. Өйткені, ең алдымен, бағдарлаудың өзі нәтижені ескере отырып қалыптасады. Екіншіден, қызметтің тиімділігі бағдар сапасына тікелей байланысты. Бұл бағдарда нәтиже құрылымы, әрекет түрі және оны орындау тәсілі нақтыланды және нақтыланды. Іс-әрекеттің дұрыстығы тексеріледі. Оқушы сол уақытта жіберген әрбір қате - болашақта мәселе шешілмейді және жаңа бағдарды іздеу мәселесі мұғалім алдында қойылады. Студент жіберетін әрбір қате басшылық принципінің толық еместігін куәландырады. Және керісінше, мұндай қателердің болмауы базалық желі толықтығының негізгі көрсеткіші болып табылады.
Кешенді басқару принципі-бұл студент бірінші және кейінгі қайталаулар кезінде дұрыс және қатесіз операцияны орындауға кепілдік беретін бағдар жүйесі.
Іс-әрекетті іске асыру басшылық бөлігінде көрсетілген іс-әрекеттерді орындауды білдіреді, нәтиже.
Оқу үрдісінде сыртқы, мақсатты, ішкі, психикалық функцияларға көшу үрдісі формация деп аталады. Қалыптастыру кезінде сыртқы іс-қимылдар өздігінен айналымға ұшырайды: қорытылады, нығыздалады және сыртқы іс-қимылдар шеңберінен шығады және әрі қарай дамиды.
Психикалық функциялардың біртіндеп қалыптасу теориясына сәйкес Дж. П. Гальперина, қалыптастыру процесі мынадай кезеңдері деп аталатын, "қадамдық шкаласы" [17]:
а) өзара іс-қимыл үшін негізді қамтамасыз ету;
б) іс-әрекеттердің толыққанды базасын құру;
в) материалдық мінез-құлықты қалыптастыру;
г) сөйлеу құралдарымен іс-қимылдарды табиғи сипаттауды қалыптастыру (дебаттар));
д) іс-әрекеттің табиғи-тілдік сипатын қалыптастыру;
д) автоматтандырылған зияткерлік қызмет түрінде іс-әрекетті қалыптастыру.
Білім сапасын арттыру, студенттерде математикалық ойлау мәдениетін қалыптастыру, білім беруде белгілі бір нәтижеге жету үшін өзін-өзі түсінуді және өзін-өзі дамытуды қамтамасыз ету үшін ғалымдар оқу процесінің технологиясына келді. Осыған байланысты педагогикалық ғылым келесі терминдерге ие: педагогикалық технологиялар, білім беру технологиялары және олар әр түрлі түсіндіріледі.
Педагогика ғылыми концепцияларды білім беру мазмұнының негізгі құрылымдық бірлігі ретінде анықтайды. Тұжырымдама тек бір жақты тәртіппен шындық әлемін ғана емес, сонымен қатар объектілердің мәнін ашады, сондай-ақ материяның маңызды қасиеттерін анықтайды, тұтас және алдау, нақты және абстрактілі бірлігін, нақты ғылымның даму нәтижесін, оның жинақталған түйіндемесін жинақтайды.
Тұжырымдама объектінің бірегей табиғатын сипаттайды, Ол жалғыз құбылыс.
Мысалы: 1) омыртқалы жануарлар тобының мүшесі;
2) радиус - шеңбердің ортасын ондағы кез келген нүктемен қосатын бөлік.
Түсінік-бұл зерттеу объектісінің жалпы, бірақ маңызды белгілері, негізгі көзқарасты құрайтын барлық белгілер ұғымы және барлық деректер жиынтығы.
Тұжырымдама өте күрделі логикалық және гнесологиялық санатты білдіреді. Бұл, біріншіден, жоғарғы материалдың жемісі; екіншіден, ол ақиқат әлемін білдіреді; үшіншіден, құрал-саймандар; төртіншіден, Тұжырымдаманың қалыптасуы сөзбен, жазумен және символдармен тығыз байланысты. Бірге тұжырымдама-бұл ойлау нысаны, "қару", ол шындық әлемін сипаттайды.
Оқу үрдісінде математикалық түсініктердің пайда болуы мен құрылымы, олардың әлемдік құбылыстар мен құбылыстармен байланысын анықтау - мұғалімнің жалғыз міндеті. Осы күрделі әдіснамалық мәселенің нәтижесінде мұғалім оқушылардың ғылыми білімін қалыптастырады. Математика бізге әлемнің белгілі бір бөлігі болып табылатын кеңістіктік қатынастар мен кеңістіктік формалар олар туралы концепцияларды зерттейтін абстрактілі объектілер мен ғылымның нысандары болып табылатынын түсінуге мүмкіндік береді.
Математикалық тұжырымдаманы қоса алғанда, кез-келген тұжырымдама заттың маңызды белгілерінің абстракциясынан да орын алады. Бірақ математикалық тұжырымдамалар материя мен құбылыстардың нақты мазмұнын елемейді және олардың барлығы үшін жалпы өлшемдік қатынастар мен формаларды ғана білдіреді. Академик А. А. Ниссанбаевтың айтуынша, "математика тек субстанцияның өзіне ғана емес, сонымен қатар оның абстрактілі құрылымы мен функцияларын да зерттейді". Математика абстрактілі объектілермен тікелей байланысты. Бірақ материалдық объект пен математикалық нысанды шатастырмау керек. Математикалық объект материалдық Объектінің нақты объектісі болып табылмайды, бірақ оның абстрактілі объектісі (нүкте, сызық, Сан, сома, топ, функция, оператор, құрылым және т.б.) күрделі абстракцияның нәтижесі болып табылады. Мысалы, егер біз бөлмедегі орын санын қарастырсақ, біз олардың сапасы мен сапасына назар аудармаймыз, тек қана санға назар аударамыз. Креслоға қанша адам қажет, қанша жаста? - Біз білгіміз келеді. Басқа нәрселерді есептей отырып, біз олардың физикалық қасиеттеріне назар аудармай, олардың санын ғана түсінеміз. Сондай-ақ, егер қандай да бір контейнердің сыйымдылығын анықтау қажет болса, біз контейнердің нысанын ескереміз және өндірілетін материалды ескермейміз. Екі қала арасындағы қашықтықты ескере отырып, біз нүктелік белгілерді түзу сызық ретінде қарастырамыз. Иірімжіптің немесе оның материалының қалыңдығы елемейді. Нәтижесінде абстракция математикалық ұғымдарға әкеледі.
Математиканың жаратылыстанудан айырмашылығы оның ұғымдарының көп кезеңді (кем дегенде екі кезеңді) түйіндемесінде тұрады.
Егер адам өзінің ақылында бірдей атрибуттары бар бірнеше нысанды біріктірсе және бұл заттарды бір атау деп атамаса, ол объективті тұжырымдаманы алмайды. Сонда бұл тұжырымдама - абстракцияның ең қарапайым нысаны - алғашқы математикалық ұғымдар абстракция арқылы пайда болады. Олардың ең маңыздысы-санның тұжырымдамасы. Мысалы, бала бұрын естіген үш сөздің арасында үш зат, үш түрлі зат (үш ойыншық, үш алма) бар екенін түсінеді. Содан кейін осы үш элементтердің әрбірінің өлшемін білдіретін "үш" санның ұғымы бірегей болып табылады.
Математикалық ұғымдардың басқа аспектісі идеализация абстракциясы болып табылады. Нүктесіз, қалыңдықсыз және т.б. алғашқы геометриялық ұғымдар абстракцияның осы түріне негізделген. Жер бетінде біз сымды немесе сым торды, ноутбук желісін және т. б. біріктіріп қана қоймай, Тұжырымдаманың мінсіз желісін біріктіре аламыз. Осылайша, "сызық" сөзі нақты кластағы объектілердің жіктелуімен ғана емес, сонымен қатар мінсіз бейнемен де шектеледі. Қайғылы әлемде үш қой, үш ағаш және тағы басқалар бар. Ұғымдар бар, бірақ математикалық түсінік жоқ. "Сызық" ұғымы заттардың жалпы қасиеттерімен бірге ортақ қасиеттерге арналған.
Абстракциялық математикалық ұғымдардың абстракциясында көптеген кубтар, тікбұрышты параллелепипедтер мен шариктер пайда болады.
Математикалық түсініктер, осылайша, математика сияқты. Енді біз екіншісінен қалыс қалу үшін математикалық тұжырымдамаларды олардың жалпы сипатымен біріктіреміз. Мысалы: барлық квадрат формаларын зерттей отырып, олар параллелограмм, тіктөртбұрыш, квадрат ұғымдарында өз атрибуттарының кез келгеніне өтеді. Бұл әлі абстракция. Бірақ мұнда материалдық әлем нысандары емес, абстрактілі математикалық ұғымдар қалыптасады.
Математикалық ұғымдардың басты ерекшелігі-олардың шынайылығы жанама емес, тікелей көрініс табады.
Математика абстракцияның екінші сатысымен шектелмейді. Көптеген математикалық ұғымдар келесі абстракция нәтижесінде құрылды. Олар жазықтықтағы және ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.