Сандық әлемдегі матрицалардың қолдану мүмкіндіктері мен есептеу әдістері


Қазақстан Республикасы білім және ғылым Министрлігі
Ы. Алтынсарин атындағы Арқалық мемлекеттік педагогикалық институты
Жаратылыстану және ақпараттандыру факультеті
Физика және математика кафедрасы
Мамандығы 5В010900-Математика
Тақырыбы: « Сандық әлемдегі матрицаның қолдану мүкіндіктері »
Жұмысты орындаған:
4 курс студенті
Сәкен Д. С.
Ғылыми жетекшісі:
аға оқытушы
Узакова Б. З.
Арқалық, 2019
КІРІСПЕ
Біздің заманымызда қоғамды дамыту үшін жеке тұлғаның алдында тұрған негізгі міндеттердің бірі - қоғам құруға өзінің бар мүмкіндігін жұмсайтын шығармашыл, қабілетті маман болу. Қазіргі таңда есептеу машиналарының математикалық ақпараттарды техникада, медицинада, экономикада, биологияда т. б кең қолданылуы, түрлі мәселелерді математикасыз шешуге болмайтындығын көрсетіп отыр.
Сондықтан да, әрбір оқушы математикалық сауатты болу үшін мынадай мақсаттар жүзеге асырылу керек. Ақыл - ойды дамыту. Математикалық іс - әрекеттің сипатына сай ойлауды қалыптастыру. Қоғамдық өмір практикасына қажетті математикалық ойлауды қалыптастыру. Математикалық білімді игеру мақсатында практикада қолдану. Болмысты, табиғат пен қоғамды тануға қажет математикалық мазмұндай білу. Алдына қойылған сұрауға немесе есепті шығаруға оптималды (жылдам, сенімді және дұрыс) жауап беруге дағдылану, ұмтылу. «Математика - ғылымдардың патшасы» деп ұлы ойшылдар айтқандай, бұл ғылым өте терең біліктер мен үлкен ізденушілікті талап етеді. Бірақ бұл ғылым өзінің қызығушылығымен қызықтыра түсетін жұмбақ тәрізді. Қиын жұмбақтың шешуін табу адамды қандай қанағаттану сезіміне бөлесе, қиын есептің шешуін тапқандығы, адамның сезімдері одан асып
Математиканың өмірмен байланысы анық. Миды жаттықтыру үшін адамға математиканы үйрену, есеп шығару, математиканың бүкіл заңдарын басқа ғылымдарды оқығанда пайдаланады. Біздің өміріміз дегенің бәрі бір - бірімен өзара байланысты. Тіршілік құбылыстарын бір - бірінен бөліп зерттеуге болмайды.
Әлдебір әлемнің сандық қатынастары мен кеңістіктік формалары, оның ішінде - структуралар, өзгерістер, белгісіздік жөніндегі ғылым - матемтика. Ол абстрактілендіру және логикалық қорыту, есептеу, санау, өлшеу және физикалық нәрселерді жүйелі түрде орнықтыру, бейнелеу мен өзгерістерді оқыту арқылы көрініс табады. Математиктер жаңа тұжырымдамаларды сипаттайтын осы түсніктерді ретімен таңдалып алынған аксиомалар мен анықтамаларды пайдалана қорыта отырып зерттейді. Сандық әлемде матиматиканың түрлі-түрлі жолдары, амалдары, әдіс-тәсілдері бар. Бұл ғажайып әлемде матрицаның мүмкіндіктері көп.
Осы мақсатты ескере отырып, математикаға қызығушылығымды арттыру барысында ойлау қабілетімді дамыту үшін әртүрлі матрицалық есептерді шешуді жүзеге асыруда мүмкіндіктерді есептеудің тәсілдерін көрсету жөн көрдім.
Ғылыми жұмыстың өзектілігі: математикалық білім мен сауаттылықтың қажеттілігін насихаттау арқылы, математика ғылымының іргелілігін, оның білім бастауының негізі екенін көрсету, қоғамның интеллектуалдық мүмкіндігінің критерийі математикалық сауаттылықтың даму қарқынына қашанда болса тәуелді болатындығына назар аударту.
Ғылыми жұмысының ғылыми жаңашылдығы: матрицалық есептерді әр түрлі әдістермен шешу жолдарына қатысты қалыпты емес есептерді шешу тәсілдері арқылы оқушылардың болашағына бағыт-бағдар беру, шығармашылық ізденісін дамыту, табиғи және дарындылық қабілеттерін шыңдау, математикалық мәдениеттіліктің деңгейін көтеру арқылы білім сапасын арттыру.
Ғылыми жұмыстың практикалық маңыздылығы: оқушылар сандар арқылы берілген матрицалық есептерді шешу және шығаруда әр түрлі әдістерді қолдана біледі, есепті шығаруға деген ынтасы артады, өз бетінше жұмыс жасауға үйренеді, логикалық және интеллектуалдық ойлау қабілеттері дамиды, орындалған жұмыстардың нәтижелеріне сыншыл көзқараспен қорытындылар жасауға үйренеді.
Ғылыми жұмыстың мақсаты: сандардан тұратын матрицалық есептердің шешу жолдарын үйрету.
Ғылыми жұмыстың міндеттері:
- матрицалық есептерді шешу жолдарына қатысты қызығушылығын арттыру;
- матрицалық есептердің шешу әдістерге қатысты шапшаң ойлауға, уақытты үнемдеуге, әр түрлі программалармен есепті оңтайлы шеше алуға үйрету.
1 САНДЫҚ ӘЛЕМДЕГІ МАТРИЦАНЫҢ ҚОЛДАНУ МҮКІНДІКТЕРІ
1. 2 Матрицалар және оларға қолданылатын амалдар
Нақты сандардан құралған m жолы және n бағанасы бар тік бұрышты сандар кестесін А матрицасы деп айтамыз.
Матрицаны белгілеу үшін дөңгелек не болмаса тік жақшаны қолданады, яғни
 немесе
немесе
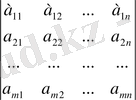
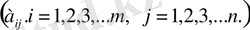
сандары матрицаның элементтері деп аталады.
Кестені әртүрлі жақшамен белгілеуге болады. Біз бірінші түрдегі жақшаны пайдаланамыз. Матрицалар латынның бас әріптерімен белгіленеді. Әрбір матрицаның элементі деп аталады. Индекстер жол мен бағанның қиылысында орналасқан элементтің жолы мен бағанының нөмірін көрсетеді.
Матрицаға қолданылатын негізгі амалдар
Матрицалардың негізгі амалдары ол:
- матрицаларды қосу,
- матрицалардың айырмасын анықтау,
- матрицаларды көбейту және матрицаны санға көбейту.
1) Бірдей өлшемді А және В матрицаларының қосындысы (айырымы) деп, элементтері А және В матрицаларының сәйкес элементтерінің қосындысына (айырымына) тең болатын сол өлшемді
матрицасын айтамыз. Яғни
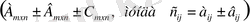
2) матрицасының санына көбейтіндісі деп (немесе санының матрицасына) сәйкес элементтері матрицасының элементінің санына көбейтіндісі болып келетін матрицасын айтамыз.

Мұнда
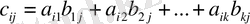 +
+ . . . +
+
+ . . . +
Матрицаларды көбейткенде, ауыстырымдылық қасиет әр уақытта сақтала бермейді, яғни
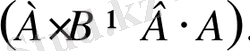
Ауыстырымдылық қасиет орындалатын матрицаларды ауыстырымды матрицалар деп атайды.
1. 2 Матрицаның түрлері
Егер
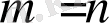 болса, яғни матрицаның жолдарының саны бағандарына тең болса, онда матрицаны n-ші ретті шаршы матрица деп атайды.
болса, яғни матрицаның жолдарының саны бағандарына тең болса, онда матрицаны n-ші ретті шаршы матрица деп атайды.
Егер матрицаның бір ғана
 жолы болса, ол матрицаны жол матрица, егер матрица бір ғана
жолы болса, ол матрицаны жол матрица, егер матрица бір ғана
 баған болса, онда ол матрицаны баған матрица деп атайды.
баған болса, онда ол матрицаны баған матрица деп атайды.
Егер шаршы матрицаның бас диагональдардың элементтерінен басқа элементтері рөлге тең болса, онда мұндай матрицаны диоганалдық матрица деп атайды.
Егер диоганальдық матрицаның бас диоганаллында тұрған элементтері бірге тең болса, онда мұндай матрицаны бірлік матрица деп атайды, яғни

Егер матрицаны бас диоганальдарының элементтерінің жоғары не болмаса төмен тұрған элементтері нөлге тең болса, онда матрицаны үшбұрышты матрица деп атайды.
Екі матрица бір-біріне тең болды, егер өлшемдері бірдей және сәйкес элементтері бір-біріне тең болса, яғни
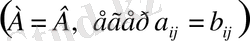 Егер А матрицаның жолын бағанмен ауыстырса, онда ол матрицаны транспонирленген (келтірілген)
Егер А матрицаның жолын бағанмен ауыстырса, онда ол матрицаны транспонирленген (келтірілген)
 матрицасы дейді.
матрицасы дейді.
Осы аталған мәліметтер бойынша төмендегідей мысалдар келтіруге болады.
1. 3 Сызықтық теңдеулерді шешу тәсілдері
1. Крамер ережесі. n белгісізді сызықтық n теңдеулердің жүйесі берілсін:α 11 x 1 + … + α 1 n x n = β 1
. . .
α n 1 x 1 + … + α nn x n = β n ,
сонымен бірге оның негізгі
А
=
 матрицасы ерекше емес болсын.
матрицасы ерекше емес болсын.
Онда жүйенің матрицалық түрі A ⋅ X = b болады,
мұндағы
b
=
 бос мүшелердің бағаны және
X
=
бос мүшелердің бағаны және
X
=
 , белгісіздердің бағаны.
, белгісіздердің бағаны.
Жүйенің жалғыз шешімі X = A -1 ⋅ b формуласымен табылады. Осыдан,
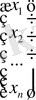 =
=

 ⋅
⋅
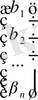 ,
,
яғни
x
1
=
 (
A
11
β
1
+
A
21
β
2
+…+
A
n
1
β
n
),
(
A
11
β
1
+
A
21
β
2
+…+
A
n
1
β
n
),
x
2
=
 (
A
12
β
1
+
A
22
β
2
+…+
A
n
2
β
n
),
(
A
12
β
1
+
A
22
β
2
+…+
A
n
2
β
n
),
⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅
x
n
=
 (
A
1
n
β
1
+
A
2
n
β
2
+…+
A
nn
β
n
) .
(
A
1
n
β
1
+
A
2
n
β
2
+…+
A
nn
β
n
) .
Бірінші теңдіктің оң жағындағы жақшадағы өрнекті
β
1
A
11
+
β
2
A
21
+…+
β
n
A
n
1
түрінде жазса, онда осы өрнек
А
1
=
 матрицасының анықтауышының ірінші бағаны бойынша жіктеуі болады. Ал
А
1
матрицасы
А
матрицасының бірінші бағаны бос мүшелер бағанымен ауыстырғанда шығады. Осыған ұқсас
А
2
матрицасы
А
матрицасының екінші бағанын бос мүшелер бағанымен ауыстырғанда шығады және т. с. с. Осыдан
матрицасының анықтауышының ірінші бағаны бойынша жіктеуі болады. Ал
А
1
матрицасы
А
матрицасының бірінші бағаны бос мүшелер бағанымен ауыстырғанда шығады. Осыған ұқсас
А
2
матрицасы
А
матрицасының екінші бағанын бос мүшелер бағанымен ауыстырғанда шығады және т. с. с. Осыдан
x
1
=
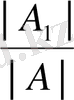 ,
x
2
=
,
x
2
=
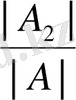 , …,
x
n
=
, …,
x
n
=
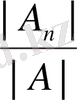 .
.
Егер n белгісізі бар n сызықтық теңдеулер жүйесінің негізгі матрицасының анықтауышы нөлден өзгеше болса, онда жүйенің жалғыз шешімі болады және шешім
x
1
=
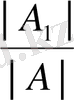 ,
x
2
=
,
x
2
=
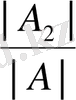 , …,
x
n
=
, …,
x
n
=
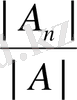 .
.
формулаларымен беріледі, мұндағы A i анықтауышы A анықтауышының i -бағанын бос мүшелер бағанымен ауыстырғаннан кейін шыққан анықтауыш.
Сызықтық теңдеулер жүйесінің матрицалық түріСызықтық теңдеулер жүйесі берілсін:
α 11 x 1 + … + α 1 n x n = β 1
. . .
α n 1 x 1 + … + α nn x n = β n .
Оның негізгі матрицасы квадрат
А
=
 матрицасы, бос мүшелер бағаны
b
=
матрицасы, бос мүшелер бағаны
b
=
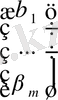 , белгісіздер бағаны
X
=
, белгісіздер бағаны
X
=
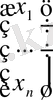 болады.
болады.
Берілген жүйені матрицалық түрде жазуға болады: A ⋅ X = b
Егер квадрат А матрицасы ерекше емес болса, онда A -1 b векторы берілген жүйенің жалғыз шешімі болады.
Баған түрінде жазылған X 0 векторы берілген жүйенің шешімі болса, онда A ⋅ X 0 = b . Осы теңдіктің екі жағын сол жақтан А -1 матрицасына көбейтсе, А -1 ( АХ 0 ) = А -1 b . Осыдан ( А -1 А ) Х 0 = А -1 b . Сондықтан X 0 = A -1 b .
Сөйтіп, берілген теңдеудің A -1 b шешімі бар, немесе шешімі болмайды.
Ал А ( A -1 b ) = b теңдігі A -1 b векторы (1) -жүйенің шешімі болатынын көрсетеді. А матрицасына кері A -1 матрицасы жалғыз болғандықтан A -1 b векторы (2) -теңдеудің жалғыз шешімі болады.
№1 мысал. Берілген жүйені матрицалық түрде жазып шешейік:
x 1 + 2 x 2 + 3 x 3 = 7
2 x 1 - x 2 + x 3 = 9
x 1 - 4 x 2 + 2 x 3 = 11
Жүйенің негізгі матрицасы
A
=
 , еркін мүшелер бағаны
b
=
, еркін мүшелер бағаны
b
=
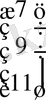 ,
,
белгісіздердің бағаны
X
=
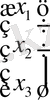 болады. Сондықтан жүйенің матрицалық түрі
A
⋅
X
=
b
болады.
болады. Сондықтан жүйенің матрицалық түрі
A
⋅
X
=
b
болады.
A
-1
=
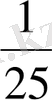
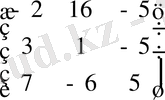 .
.
Осыдан жүйенің шешімі табылады:
X
=
A
-1
⋅
b
=
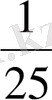
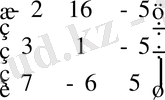 ⋅
⋅
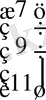 =
=
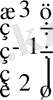 .
.
№2 мысал. Теңдеулер жүйесін Крамер ережесімен шешейік:
x 1 + 2 x 2 + 3 x 3 = 7
2 x 1 - x 2 + x 3 = 9
x 1 - 4 x 2 + 2 x 3 = 11
∆ =
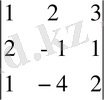 =
=
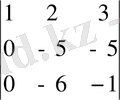 =
=
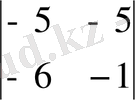 = 5 - 30 = - 25 және ∆
1
= -75,
= 5 - 30 = - 25 және ∆
1
= -75,
∆ 2 = 25, ∆ 3 = -50. Осыдан x 1 = 3, x 2 = -1, x 3 = 2.
№3 мысал. AX = C теңдеуінен Х матрицасын табайық, мұндағы
A
=
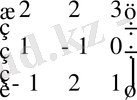 ,
C
=
,
C
=
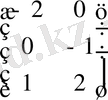
.
Теңдеуді сол жағынан A -1 матрицасына көбейтсе,
онда А -1 АХ = А -1 С . Ал А -1 А = Е және ЕХ = Х .
Сондықтан Х = А -1 С .
Кері А -1 матрицасын табайық. Ол үшін А матрицасының оң жағына бірлік Е матрицасын жазып, үлкен ( А Е ), А матрицасының орнына бірлік Е матрицасына келгенше элементар түрлендірулерді жасай беру керек.
Онда оң жағында Е бірлік матрицасының орнында кері А -1 матрицасы шығады:
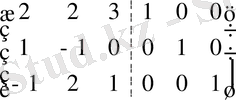 ~
~
 ~
~
 ~
~
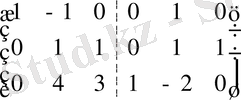 ~
~
 ~
~
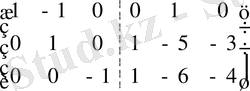 ~
~
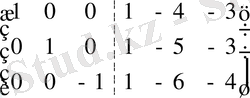 ~
~
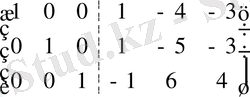 .
.
Осыдан
A
-1
=
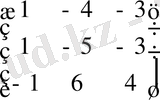 .
.
Енді Х матрицасын табуға болады:
Х
=
А
-1
⋅
С
=
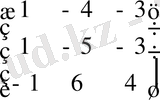 ⋅
⋅
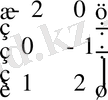 =
=
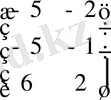
№4 мысал.
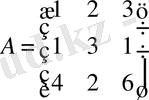 және
және
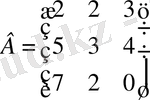 матрицаларының қосындысын және айырмасын есептеңіз.
матрицаларының қосындысын және айырмасын есептеңіз.
Шешуі:
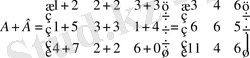
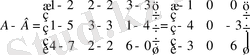
№5 мысал.
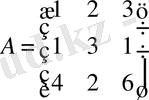 және
және
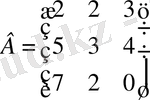 матрицаларының көбейтіндісін есептеңіз.
матрицаларының көбейтіндісін есептеңіз.
Шешуі:
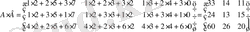
№6 мысал.
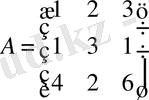 және
және
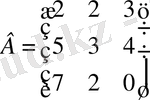 матрицаларын
матрицаларын
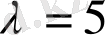 санына көбейткендегі мәнін табу керек.
санына көбейткендегі мәнін табу керек.
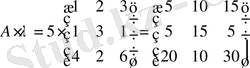
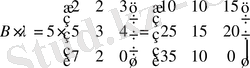
№7 мысал.
Берілген сызықтық теңдеулер жүйесін Крамер, Гаус және матрицалық әдістермен шешу керек.
а) Берілгені:
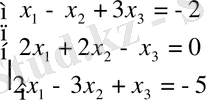
Шешуі: Крамер әдісімен
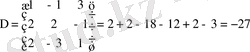
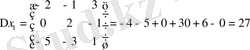
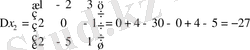
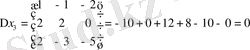
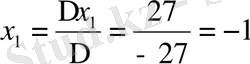
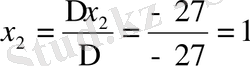
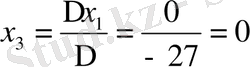
Жауабы:
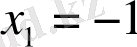
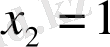
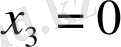
б) Берілгені:
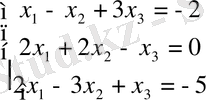
Шешуі: Гаус әдісімен

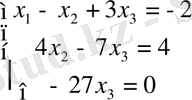
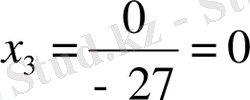
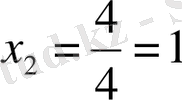
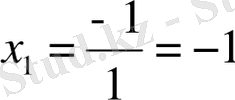
Жауабы:
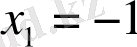
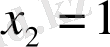
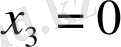
2 МАТРИЦАЛЫҚ ЕСЕПТЕРДІ ШЕШУДЕГІ ҚОЛДАНЫЛАТЫН ПРОГРАММАЛАР
2. 1 "Matrix Calculator" программаны қолданып матрицалық есептерді шығару
Жоғарыда айтылған матрицаларды осы аталған программаның көмегімен матрицаларға амалдар орындауға, шешуге болады (1, 2, 3, 4 суреттерде көрсетілгендей) .
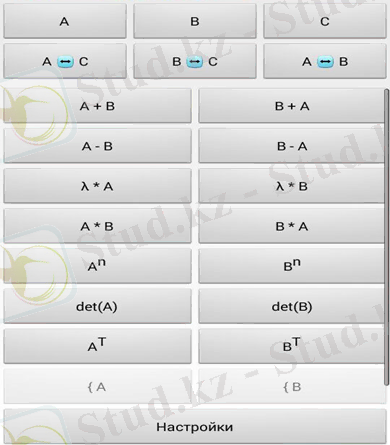
Сурет 1. "Matrix Calculator" программаны есеп шығаруда қолданылуы
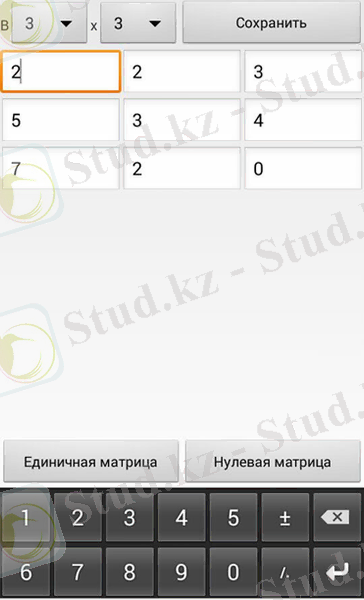
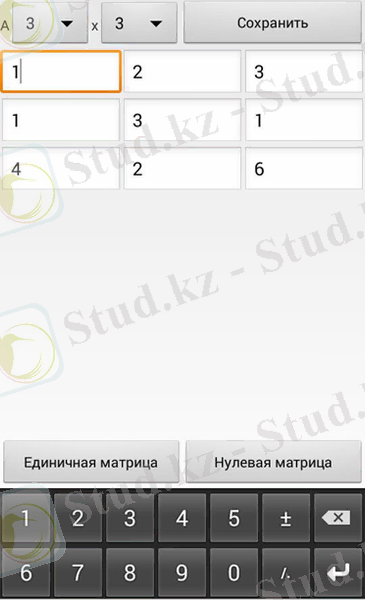
Сурет 2. А және В матрицаның элементтерін толтыру

Сурет 3. Матрицаларға амалдар қолданылуы
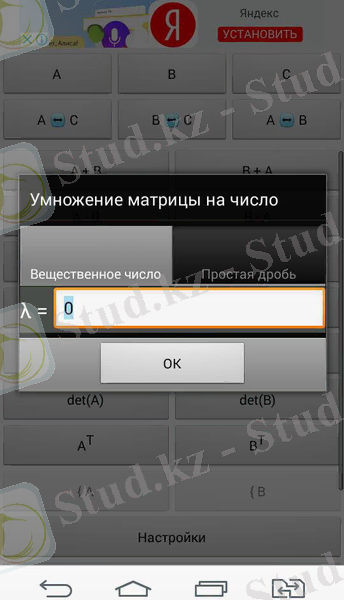
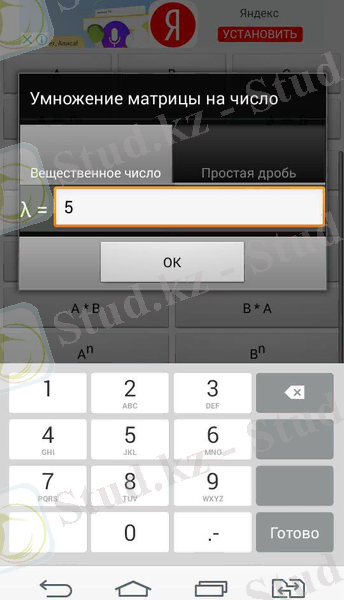
Сурет 4. Матрицаларды санға көбейту үшін программаның қолданылуы
Жоғарыда аталған матрицаларды шешуде қолданылған программалардың шығару жолдары (5, 6, 7 суретте көрсетілгендей) .
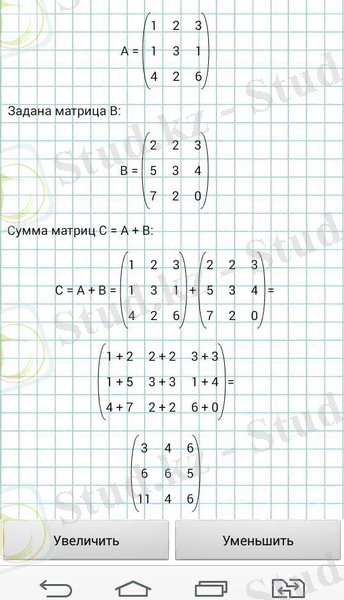

Сурет 5. Матрицаларды қосу және азайту


Сурет 6. Матрицаны матрицаға көбейту


Сурет 7. Матрицаны санға көбейту
2. 2 "Решение матриц" программасының көмегімен шешу
Ендігі Решение матриц программасының шығару жолы төменде көрсетілген (8, 9 сурет)


Сурет 8. "Решение матриц" негізгі құрылымы.
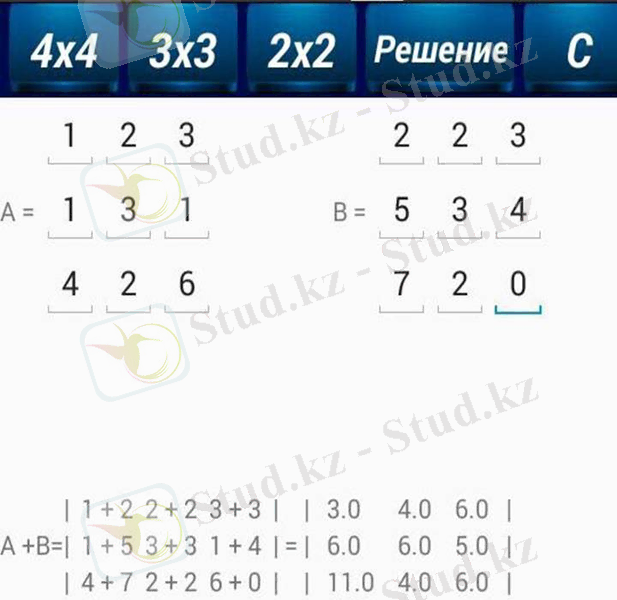
Сурет 9. Матрицаның шығару жолдары
2. 3 "Решение уравнений и матриц" программасы арқылы сызықтық теңдеулер жүйесіндегі матрицалық әдісмен шешу тәсілі
Сызықтық теңдеулер жүйесін "Решение уравнений и матриц" программасы арқылы шешуге болады (10, 11, 12 суреттер)

Сурет 10. "Решение уравнений и матриц" негізгі беті
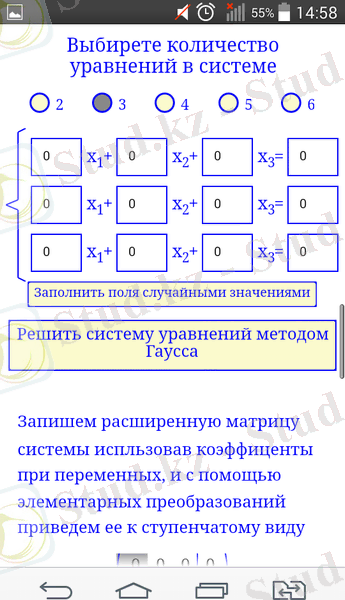
Сурет 11. Тецдеулер жүйесін Гаусс әдісімен шешу

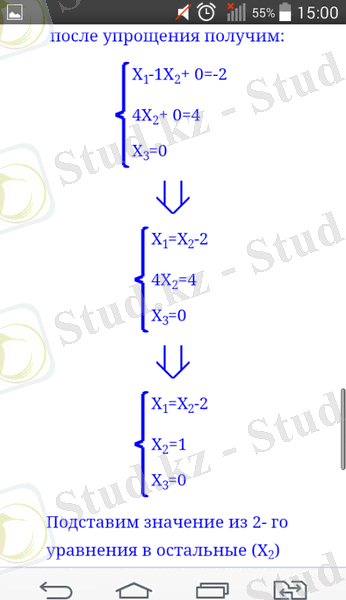

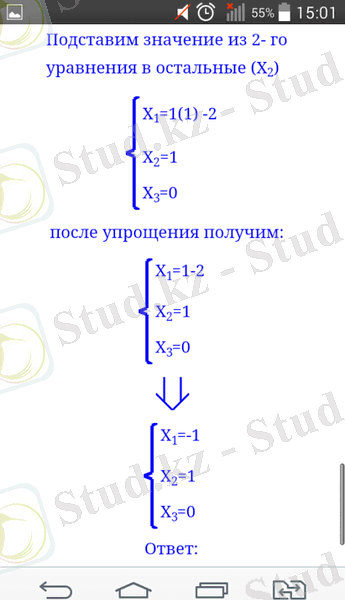
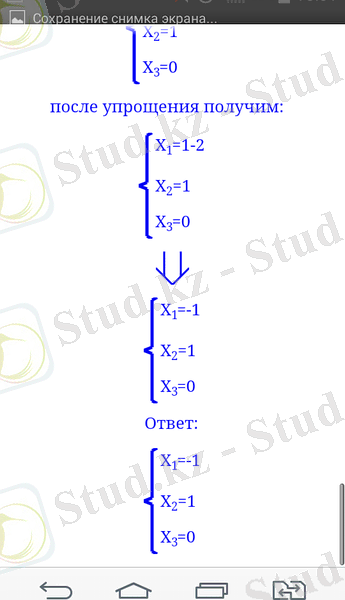
Сурет 12. Сызықтық теңдеулер жүйесінің шығару жолыдары.
2. 4 Экономикалық есептерді шығаруда матрицаның қолданылуы
Күнделікті тәжірибемізден көріп жүргеніміздей, заманауи қаржыгер маманға тереңдетіліп оқытылған математикалық білім керек. Ең маңызды математикалық қажетті пәннің біреуі ол сызықты алгебра, нақтырақ айтсақ матрицалық алгебра. Бұл сөзімізге дәлел ретінде экономикалық - математикалық модельдердің жоспарлы - зерттеу жұмыстарында, экономикалық құрылымдар арасында байланыс орнатуда қолданылып жүргенін айтуымызға болады. Қолдануға ыңғайлы, алға қойған тапсырмаларды шешуде қолданылатын тәсілдердің бірі матрицалық бейнелеу болып табылады. Көпшілігіміз білетіндей матрица дегеніміз m жолмен, n бағаннан, сандардан тұратын тікбұрышты таблица. Қарапайым тілмен айтқанда матрица деп тікбұрышты таблица түрінде жазылатын математикалық нысан. Бізге матрицаны матрицаға көбейту, транспонирлеу, қосу, матрицаны санға көбейту секілді негізгі операциялар белгілі. Матрица туралы ұғым алғашында XVII ғасыр ортасында ағылшын математиктері А. Кэли мен У. Р. Гамильтон жұмыстарында кездесті. Одан кейін матрицаның жалпы теориясын жазуда орыс математиктері А. Н. Крылов, Лапло - Данилевский көптеген еңбек сіңірді. Қарапайым тұрпаты мен бай экономикалық мазмұны бар матрицалық әдіс экономикалық тәжірибеде көп қолданыс тапты, мысалы: статистикалық есеп, документтік айналым жұмыстарынын қысқаруы, ішкі шаруашылық жұмыстарының есебі, экономикалық анализ жүргізуде т. б. Матрицалық әдісті халық шаруашылығы, мемлекет экономикаларын модельдеуде кеңінен қолдануға болады. Ондай типтегі матрицалар саларалық баланс деген атқа ие болып, жоспарлау және статистика жұмыстарында кеңінен қолданылады. Осыдан кейін экономикалық қызметте жоғарғы дәрежеде талдау әдісі қолданылады деген тұжырымға келеміз. Мұндай әдіс экономикалық жайттарды талдау мақсатында қолданылып отыр. Бұл тәсілдер көбіне салыстырмалы бағалау, ұйымдардың құрылымдық бөлімшелерінің жұмыс істеу функцияларын ретке келтіру мақсатында қолданыс тауып отыр. Экономикада матрицалық әдіс бұл - матрицаларды қолдану ережелерінің теориясы негізіне сүйеніп, нысан құрылымын ғылыми зерттеу әдісі. Бұл жерде модель элементтерінің мақсаты анықталып, экономикалық нысандардың өзара байланысын айқындайды. Басты зерттеу нысаны өндірістік - шаруашылық қызметтер нәтижелері, шығындардың және шығарған өнім нормативтері арасында баланстық шығын арақатынасы болған кезде кеңінен қолданылады. Матрицалық әдіс қолданып шығарылатын экономикалық есептер кез келген кәсіпорын мен экономикалық саланың басты есептерін шешуге жол ашты.
Матрицаны қолданып экономикалық есепті шешуді
қарастырайық:
Кәсіпорын өнімнің үш түрін
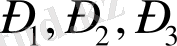 , ал оны өндіру үшін екі түрлі
, ал оны өндіру үшін екі түрлі
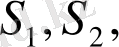 шикізат қолдансын. Шикізат шығыны нормасы мына матрицамен берілcін:
шикізат қолдансын. Шикізат шығыны нормасы мына матрицамен берілcін:
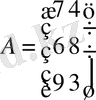 ,
,
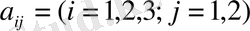 әрбір элементі өнімнің
i
түрін өндіруге шикізат бірлігінің қанша
j
түрі жұмсалатынын көрсетеді. Өнім өндіру жоспары C=(125 85 190) матрицамен жол түрінде берілсін.
әрбір элементі өнімнің
i
түрін өндіруге шикізат бірлігінің қанша
j
түрі жұмсалатынын көрсетеді. Өнім өндіру жоспары C=(125 85 190) матрицамен жол түрінде берілсін.
Әр шикізат құны (ақша бірлігі) матрицамен баған түрінде
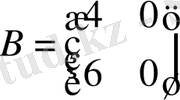 берілсін делік. Шикізаттың ортақ құнын есептеу керек. Енді осы берілген есепті шешейік: Бірінші шикізатқа кеткен шығын құны,
берілсін делік. Шикізаттың ортақ құнын есептеу керек. Енді осы берілген есепті шешейік: Бірінші шикізатқа кеткен шығын құны,
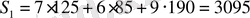 , ал екінші шикізатқа кеткен шығын құны
, ал екінші шикізатқа кеткен шығын құны
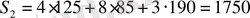 . Демек, шикізат шығыны
S
матрицамен мына түрде жазылады (3095 1750) .
. Демек, шикізат шығыны
S
матрицамен мына түрде жазылады (3095 1750) .
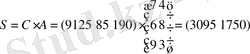
Шикізаттың ортақ құны
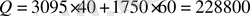 (ақша бірлігі) мына түрде жазылады:
(ақша бірлігі) мына түрде жазылады:
 .
.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz