Матрицалар мен анықтауыштар және олардың алгебралық теңдеулер жүйелерін шешудегі қолданылуы


Мазмұны
Матрицалық әдіс арқылы сызықтық алгебралық теңдеулер
жүйесін шешу . . .
Кіріспе
Мектеп алгебра және геометрия курсын оқытудың негізгі мақсаттарының бірі -- оқушыларға алгебра және геометрияның теориялық негіздерін үйрету және оларды практикада қолдана білу дағдыларын меңгерту. Сонымен қатар оқушылардың логикалық ойлауын, дәлелдеу қабілетін, талқылауларды негіздей білу болып табылады.
Тақырыптың көкейкестілігі Мектеп алгебра және геометрия курсының көкейкесті мәселелері - курстың мазмұнының ғылыми құндылығын арттыру және оның негізінде оқушылардың пәнге деген қызығушылығын арттырып, өз бетінше іздену, шығармашылық іс-әрекеттерге тарту және т. с. с.
Мектеп математика курсын оқыту үрдісінде оқушыларды математикалық ұғымдардың анықтамаларын дұрыс және дәл тұжырымдауға үйретуге ерекше назар аударылады. Өйткені, математикалық ұғымдарға дәл анықтама беруге үйрету арқылы оқушылардың математикалық білімдерді саналы игеруі қамтамасыз етіледі, олардың логикалық ойлауы жетілдіріле түседі.
Алгебра және геометрия есептерін шешу әдістемесі мәселесiне, оның негiзгi белгiлерi мен сипаттамаларын анықтауға В. Г. Афанасьев және т. б. философтардың, В. В. Давыдов, Г. Е. Журавлев, Е. И. Машбиц сынды психологтардың, С. И. Архангельский, Е. Ы. Бидайбеков, Ж. А. Қараев және т. б. педагогтардың еңбектерi арналған.
Мен өзімнің курстық жұмысымда - анықтауыштар мен матрица ұғымдарын пайдалана отырып кейбір қиындығы жоғары теңдеулер жүйесін шешуге берілген есептерді шешуде матрицалық әдісті пайдалана отырып шығару жағдайларын тереңірек сараптауға арнай отырып, мынадай мақсат қойылды.
Курстық жұмыс мақсаты Алгебралық теңдеулер жүйесіне берілген есептерді шешудің негізгі әдістері, кейбір стандартты емес дербес жағдайларын сараптай отырып, кейбір тұжырымдар мен қағидаларды өзбетінше дәлелдеуге әрекеттену.
Ендігі біздің мақсатымыз кейбір шешілу жолдары ұзақ, уақыт жағынан тиімсіз алгебралық теңдеулер жүйесін шешуде стандарт емес тәсілдерді, яғни кейбір алгебралық теңдеулер жүйесін шешкенде геометриялық ұғымдарды қолдансақ, онда біз есеп шғару барысында оқушыларға түсінікті, шығарылу жолдары тиянақты, уақыт жағынан ұтымды тәсілді тапқан болар едік. Нақтырақ айтқанда, косинустар теоремасын, Пифагор теоремасын, үшбұрыштың медианасының және биссектрисасының ұзындығын есептеу формулаларын, шеңберге іштей сызылған төртбұрыштың бұрыштарының және қабырғаларының арасындағы қатынасын қолданып, үш белгісізді үш теңдеулер жүйесін және тағы сол сияқты алгебралық есептерді оңай және түсінікті етіп шығаруға баулу.
Осы мақсатқа сәйкес мынадай негізгі міндеттер қойылды:
- Алгебралық теңдеулер жүйесін шешудің тәсілдері мен қасиеттеріне тоқталу;
- Геометрияның негізгі ұғымдары мен тұжырымдарын, фигуралары және олардың қағидаларын оқып-үйрену;
- Теңдеулер жүйесін шешуде жаңа әдістерді пайдалану.
Ғалымдардың мектепке жасаған тәжірибелерін, мұғалімдермен, оқушылармен жүргізген сауалнамаларын, сондай-ақ автордың педагогикалық және мемлекеттік іс-тәжірибелерін байқауларын сараптай келе алгебралық теңдеулер жүйесіне берілген есептерді шығарудың негізгі әдістерін пайдаланудың шарттарын, дидактикалық принциптерін, тиімділігін, қолайлылығын ашып көрсету.
Курстық жұмыстың тақырыбы «Матрицалар мен анықтауыштар және оларға қолданылатын амалдар» деп аталады. Яғни, анықтауыштар мен матрицалар ұғымдары мен оларға геометриялық ұғымдардың қасиеттерін пайдалана отырып, оқушыларға алгебра есептерін шешуді үйрету жолдары туралы айтылады.
Кіріспеде зерттеудің ғылыми аппараты: зерттеу тақырыбының мақсаты, міндеттері, дипломдық жұмысының практикалық мәні, ғылыми жаңалығы мен қорғауға ұсынылатын тұжырымдар баяндалады.
Қорытындыда зерттеу тақырыбы бойынша қорытынды тұжырымдар келтірілген.
Пайдаланылған әдебиеттер тізімінде зерттеу барысында талданған, қарастырылған әдебиеттер жинақталған.
1 Анықтауыштар және матрицалар
1. 1 Анықтауыш және матрица ұғымдары
Сызықтық алгебра - бірінші дәрежелі (сызықты) теңдеулер жүйесін зерттейді. Мұндай жүйелерді шешу үшін, теңдеулер саны белгісіздер санына тең болған жағдайда анықтауыштар теориясының аппараты қолданылады. Бұл аппарат жүйедегі тендеулер саны, белгісіздер санына тең емес болса жарамайды. Осы сияқты жағдайлар матрицалар теориясын, яғни, квадрат немесе тік бұрыш кестелерде орналасқан сандар жиынтығын пайдалану қажеттігін туғызды. Матрицалар теориясы өмірдің басқа салаларында да аса маңызды болып шықты. Мысалы, матрица -- ғылыми техникалық және экономикалық есептерде кестелік ақпараттарды жазу үшін қолданылады; бағдарламалау саласында матрицаларды екі өлшемді массивтер деп атайды.
n белгісізі бар m сызықтық алгебралық теңдеулер жүйесі келесі түрде жазылады:
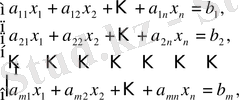 (1)
(1)
мұндағы:
х 1 , х 2 , . . . , х n -- жүйе белгісіздері;
а ij , і = 1, 2, . . . , m ; j = 1, 2, . . . , n -- жүйе коэффициенттері;
b j , і = 1, 2, . . . , m -- бос мүшелер деп аталады.
Жүйе коэффициенттерінен тік бұрышты кесте құрауға болады. Ол кестені белгілеуге келесі
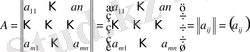 (2)
(2)
символдардың бірін қолданады.
Бұл кестені m жол және n бағаннан тұратын m×n өлшемді матрица деп атайды. Мұндағы а ij , і = 1, . . . , m ; j = 1, . . . , n - матрица элементтері деп аталады және ол і - жол мен j - баған қиылысуында тұрады.
Егер n = m болса, онда (2) кесте
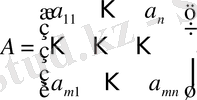 (2
/
)
(2
/
)
түріне ие болады және ол n ретті квадрат матрица деп аталады ( n = m санын квадрат матрицаның реті дейді) . Мұндағы а ij , і = 1, 2, . . . , n -- бас диагональ , ал a 1n , a 2(n-1) , …, a n1 -- бүйір диогональ элементтері деп аталады.
Дербес жағдайда, n = m = 2 болса, (1) жүйе
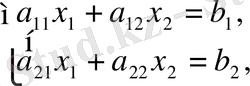 (3)
(3)
түрінде жазылады. Бұл жүйенің коэффициенттері
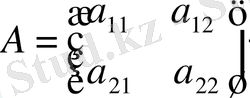 (4)
(4)
түріндегі екінші ретті квадрат матрицаны құрайды. (3) жүйенің бірінші және екінші тендеулерінің екі жақ бөліктерін сәйкес а 22 мен а 12 - ге көбейтіп, шыққан нәтижелерін мүшелеп шегерсек
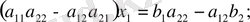
ал ол теңдеулерді сәйкес
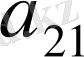 мен
мен
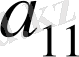 сандарына көбейтіп, шыққан нәтижелерін мүшелеп шегерсек
сандарына көбейтіп, шыққан нәтижелерін мүшелеп шегерсек
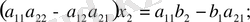
аламыз. Егер
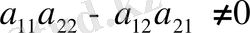 болса, онда (3) жүйенің шешімі
болса, онда (3) жүйенің шешімі
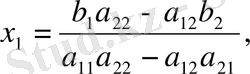
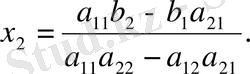 (5)
(5)
Бұлардың ортақ бөлімі, (4) матрица элементтері арқылы өрнектеліп тұр:
 саны - бас диагональ элементтерінің көбейтіндісі, минус бүйір диагональ элементтерінің көбейтіндісі.
Бұл сан, (4)
матрицаның анықтауышы
(немесе
детерминанты
(ағыл. анықтауыш) ) деп аталады. (4) матрица екінші ретті болғандықтан
саны - бас диагональ элементтерінің көбейтіндісі, минус бүйір диагональ элементтерінің көбейтіндісі.
Бұл сан, (4)
матрицаның анықтауышы
(немесе
детерминанты
(ағыл. анықтауыш) ) деп аталады. (4) матрица екінші ретті болғандықтан
 саны да екінші ретті анықтауыш деп аталады. (4) матрицаның анықтауышын белгілеу үшін матрицадағы жай жақшаның орнына тік таяқшаларды қолданады және анықтауышты
detA
немесе ∆ арқылы белгілейді
саны да екінші ретті анықтауыш деп аталады. (4) матрицаның анықтауышын белгілеу үшін матрицадағы жай жақшаның орнына тік таяқшаларды қолданады және анықтауышты
detA
немесе ∆ арқылы белгілейді
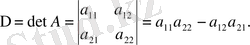 (6)
(6)
Мысалдар
1)
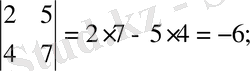
2)
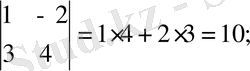
(5) теңдіктерді келесі түрде жазуға болады
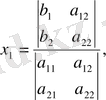
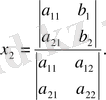 (7)
(7)
(3) жүйені (7) формулалар арқылы шешу - Крамер ережесі деп аталады.
Енді үш белгісізі бар үш теңдеулер жүйесін қарастырайық
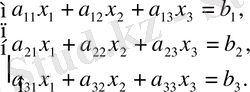 (8)
(8)
Бұл жүйенің коэффициенттерінен келесі
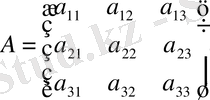 (9)
(9)
үшінші ретті (n=m=3) матрицаны
құрауға болады. (8) жүйенің мысалы, х
1
-нші белгісізін табу үшін осы үш теңдеудің екі жағын сәйкес
 ,
,
 ,
,
 сандарына көбейтіп, шыққан нәтижелерді мүшелеп қоссақ, келесі теңдікті аламыз
сандарына көбейтіп, шыққан нәтижелерді мүшелеп қоссақ, келесі теңдікті аламыз
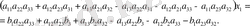 (10)
(10)
Мұндағы х 1 -дің коэффициентін, (9) матрицаның (үшінші ретті) анықтауышы деп атайды. Сонымен
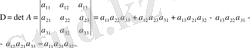 (11)
(11)
теңдіктегі қосылғыштарды келесі схема арқылы құрауға болады (оны үшбұрыш немесе Саррюс ережесі деп атайды)
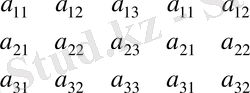
Мысалы
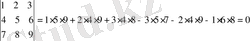
Жалпы жағдайда, n-ретті анықтауыш мына түрде
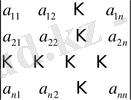
белгіленеді (оның анықтамасын төменде келтіреміз) .
(11) тендіктегі таңбасымен бірге алынған әрбір қосылғыш анықтауыш мүшесі деп аталады. Әрбір мүшеде әрбір жол мен әбір бағанның бір-бірден элементтері бар. Бұл элементтерді олардың бірінші индексінің (элемент жатқан жол нөмірінің) өсу ретімен орналастыруға болады. (11) тендік дәл осылай жазылған.
Анықтама А матрицасының жолдарын сәйкес бағандар етіп, орын алмастырудан алынған А Т матрицасы транспонирленген немесе аударылған матрица деп аталады .
А мен А Т матрицаларының элементтері бас диагоналға салыстырғанда симметриялы.
Жолдарды бағандармен алмастыру амалы транспонирлеу немесе аудару деп аталады.
∆ анықтауышынан аудару арқылы алынған анықтауышты ∆* арқылы белгілейтін боламыз.
Енді анықтауыштардың қасиеттерін қарастырамыз.
1. 2 Анықтауыштардың қасиеттері
Оқушының түсінуіне жеңілдеу болуы үшін, алғашқы қасиеттерді екінші ретті анықтауыштар үшін қарастырамыз. Олар үшінші, жалпы, n-ші ретті анықтауыштар үшін де орындалады.
1° Анықтауыш пен оны аудару арқылы алынған анықтауыш өзара тең: ∆=∆*. Мысалы,
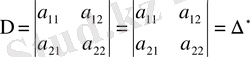
2° Анықтауыштың параллель қатарларын өзара орын алмастырса анықтауыш таңбасы өзгереді. Мысалы
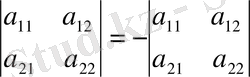
3° Анықтауыштың қандай да бір қатарының барлық элементтері k санына көбейтілсе, анықтауыш мәні k есе артады. Басақаша айтқанда, қатардың ортақ көбейткішін анықтауыш алдына шығаруға болады. Мысалы
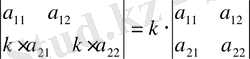 .
.
Назар аударыңыз Анықтауышты санға көбейту үшін оның қандай да бір қатар элементтерін осы санға көбейтсе болғаны.
4° Анықтауыштың қандай да бір қатарының барлық элементтері нөлге тең (нөл қатар) болса, анықтауышта нөлге тең. Мысалы
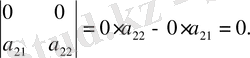
5° Анықтауыштағы параллель қатарлардың сәйкес элементтері тең болса, ол нөлге тең. Мысалы,
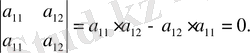
3° және 5° қасисттерден келесі қасиет шығады.
6° Анықтауыштағы параллель қатарлардың сәйкес элементтері пропорционал болса, анықтауыш нөлге тең. Мысалы,
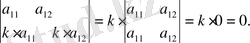
Бұдан кейінгі қасиеттерді үшінші немесе n -ші ретті анықтауыштар үшін тұжырымдайық.
Анықтама А матрицасындағы а ij элементінің миноры деп осы элемент тұрған жол мен бағанды алып тастап, оның қалған қатарларынан құралған матрицаны айтамыз және оны ма ij арқылы белгілейміз.
Минор түсінігін анықтауыштар үшін де қолданады.
Анықтауыштың а ij элементінің минорын М ij арқылы белгілейміз.
Мысалы
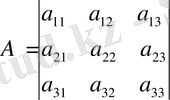 болса, онда
болса, онда
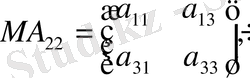
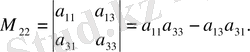
Анықтама Анықтауыштың а ij элементінің алгебралық толықтауышы немесе адъюнкті деп
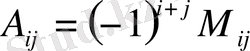
санын айтады.
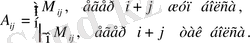
Мысалы
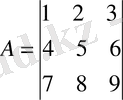 матрицасы үшін
матрицасы үшін
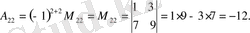
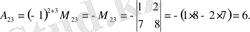
Келесі қасиет, реті кез - келген анықтауышты анықтауға мүмкіндік береді.
7° Анықтауыштың қандай да бір қатарының элементгері мен олардың сәйкес алгебралық толықтауыштарының көбейтінділерінің қосындысы осы анықтауыш шамасына тең:
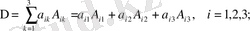 (12)
(12)
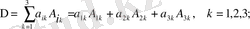 (13)
(13)
Бұл қасиетті 3-ші ретті анықтауыштың, мысалы, 3-ші жол элементтері үшін дәлелдейік.

(12) қосынды, анықтауыштың і-нші жол элементтері бойынша жіктелуі, ал (13) қосыңды, анықтауыштың k-ші баған элеметтері бойынша жіктелуі деп аталады.
1-ескерту Анықтауыштың қандай да бір қатарының бір элементінен басқа элементтері нөл болса, анықтауыштың жіктелуі жалғыз қосылғыштан тұрады. Мысалы, а 21 = а 31 = 0 болса, онда
∆=а 11 А 11 .
2-ескерту Егер анықтауыштың бас диагоналінің астындағы немесе үстіңдегі барлық элементгер нөлге тең, яғни а kl = 0, k > l немесе а кl = 0, k < l болса, онда анықтауыштың мөні бас диагональ элементтерінің көбейтіндісіне тең: ∆ = а 11 ⋅а 22 ⋅а 33 .
Егер бүйір диагональ үстіндегі немесе астындағы барлық элементтер нөлге тең болса, онда ∆ = -а 13 ⋅а 22 ⋅а 31 .
Назар аударыңыз 2-ескертудегі тұжырым n -ретті анықтауыштар үшін сейкес,
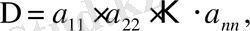
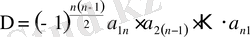
түрлерінде жазылады.
2- ескерту 1-ескертуден шығады.
1-мысал
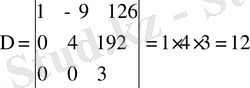
2-мысал
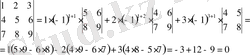
Анықтама n-ші ретті
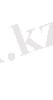
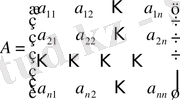
матрицасының анықтауышы деп жіктелу туралы 7° қасиетті және анықтауыштың басқа да қасиеттерін пайдалана отырып алынатын санды айтады және оны
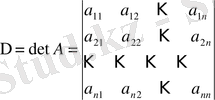 символымен белгілейді.
символымен белгілейді.
Бұл анықтама қисынды (корректно) екенін, яғни, есептеу нәтижесі жоғарыдағы аталған қасиеттерді қандай ретпен және қандай қатарға қолданылғанына тәуелсіз, бір мәнді табылатынын көруге болады.
8° Анықтауыштың қандай да бір қатар элементтері мен осы қатарға параллель басқа қатардың сәйкес элементтерінің алгебралық толықтауыштарының көбейтінділерінің қосындысы нөлге тең.
Мысалы
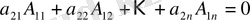 (14)
(14)
екенін көрсетейік. (14) тендіктің сол жағындағы өрнекте
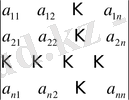
анықтауышының бірінші жол элементтерінің бірде-бірі жоқ, демек бұл өрнек бірінші жол элементтеріне тәуелсіз. Сондықтан, бірінші жолға кез-келген элементтерді жаза аламыз. Олай болса,
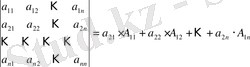
Бұл тендіктің сол жағындағы анықтауыштың бірінші және екінші жолдары өзара тең, сондықтан ол анықтауыш нөлге тең, яғни, (3) тендік орындалады.
9°. Егер анықтауыштың белгілі бір қатарының әрбір элементі екі қосылғыштың қосындысы етіп берілсе, онда анықтауыш екі анықтауыштың қосындысына тең. Бірінші анықтауыштың сәйкес қатары бірінші қосылғыштардан, ал екінші анықтауыштың сәйкес қатары екінші қосылғыштардан тұрады да, бұл екі анықтауыштың қалған қатарларының элементтері бастапқы анықтауыштың сәйкес элементтеріне тең болады.
Мысалы
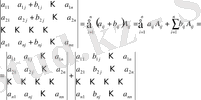
10° Егер анықтауыштың қандай да бір қатарының барлық элементтеріне осы қатарға параллель қатардың сәйкес элементтерін кез-келген k санына көбейтіп қосса, онда анықтауыш мәні өзгермейді.
Бұл қасиеттің дұрыстығын 9°, 5° және 3° қасиеттерді қолдана отырып көз жеткізуге болады.
Мысал Есептеу керек:
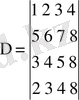
Жоғарыдағы 1-мысалға сай а 21 , а 31 , а 41 элементтерін нөлге келтірейік. Ол үшін 7° бойынша 1-ші жолды кезек-кезек -5, -3 және -2 сандарына көбейтіп, сәйкес, 2- ші, 3- ші және 4- ші жолдарға қоссақ
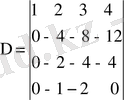
болады. Бұған 7°, 5° және 6° қолданып

аламыз.
2 Анықтауыштар мен матрицаларға амалдар қолдану
2. 1 Матрицаларға амалдар қолдану
Матрицаларға жасалатын келесі амалдарды қарастырамыз: санға көбейту, қосу, көбейту және кері матрица табу.
Алдымен келесі түсініктерді енгізейік.
Квадрат матрицаның бас диагональ элементтерінен басқа элементтердің барлығы нөлге тең болса, оны диагональ матрица дейді. n -ші ретті диагональ матрицаны келесі түрде жазуға болады.
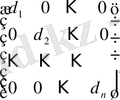
Егер мұнда d 1 =d 2 = . . . = d n =d болса, онда d=1 және d =0 үшін диагональ матрица, сәйкес, бірлік матрица және нөлдік матрица деп аталады:


Ескерту Нөлдік матрица түсінігі кез-келген тік бұрышты (квадрат емес) матрицалар үшін де енгізіледі.
Анықтама
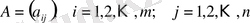 матрицасы
мен λ
санының көбейтіндісі
(λА)
деп әрбір элементі
матрицасы
мен λ
санының көбейтіндісі
(λА)
деп әрбір элементі
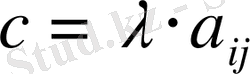 тең
тең
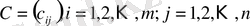 матрицасын айтады.
матрицасын айтады.
1-мысал
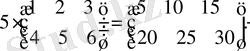
Бұл амал үшін келесі қасиеттер орындалады:
- (λμ) А=λ(μА) (сандық көбейткіштерге қатысты ассоциативті) ;
- (λ+μ) А=λА+μА (сандық қосуға қатысты дистрибутивті) ;
Сонымен бірге, 1⋅А=А, (-1) ⋅А=-А, 0⋅А=0 теңдіктері орындалады.
Анықтама
Бірдей өлшемді А және В матрицаларының қосындысы деп, әрбір элементі
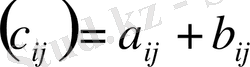 тең, өлшемі А (немесе В) матрицаның өлшеміндей
тең, өлшемі А (немесе В) матрицаның өлшеміндей
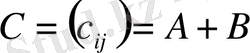 матрицасын айтады
.
матрицасын айтады
.
2-мысал
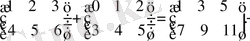
Матрицаларды қосу амалы үшін келесі қасиеттер орындалады:
- А+В=В+А (коммутативтік) ;
- (А+В) +С=А+(В+С) (ассоциативтік) ;
- λ(А+В) =λА+λВ (матрицаларды қосуға қатысты дистрибутивтік) .
Назар аударыңыздар Матрицаларға жасалған бұл екі амал, анықтауыштар үшін тек таңдалған бір қатар элементтеріне ғана қатысты орындалатын еді.
Анықтама
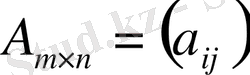 және
және
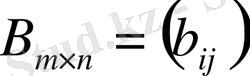 матрицаларының көбейтіндісі
деп,
матрицаларының көбейтіндісі
деп,
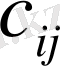 элементтері
элементтері
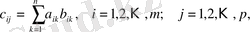 (1)
(1)
тең яғни, і-ші жол мен j-ші баған қиылысуындағы
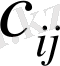 элементі А матрицасының і-ші жолы мен В матрицасының j-шi бағанының сәйкес элементтерінің көбейтінділерінің қосындысына тең болатын
элементі А матрицасының і-ші жолы мен В матрицасының j-шi бағанының сәйкес элементтерінің көбейтінділерінің қосындысына тең болатын
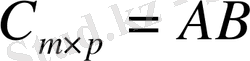
матрицасын айтады.
Ескерту Анықтамадан, 1-ші матрицаның бағандар саны 2-ші матрицаның жолдар санына тең болатын және тек қана сондай матрицаларды ғана көбейтуге болатынын көреміз.
3-мысал
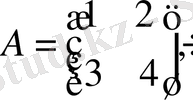 Equation. 3
Equation. 3
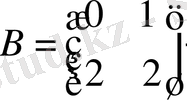 Equation. 3 берілген. АВ және ВА табу керек.
Equation. 3 берілген. АВ және ВА табу керек.
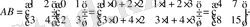
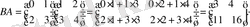
Бұл мысалдан АВ≠ВА, яғни матрицаларды көбейту коммутативті емес екені көрінеді.
Матрицаларды көбейту амалы келесі қасиеттерге ие:
- (АВ) С = А(ВС) (ассоциативті) ;
- (А + В) С = АВ + ВС (матрицаларды қосуға қатысты дистрибутивті) ;
3) Квадрат матрицалар үшін det(AB) =detA-detB, яғни, көбейтіндінің анықтауышы, көбейткіштердің анықтауыштарының көбейтіңдісіне тең.
Сонымен бірге, кез- келген квадрат А матрица үшін
АЕ = ЕА = А, А⋅0=0⋅А =0,
яғни, Е бірлік матрицасы бірлік сан сияқты, ал нөл матрица нөл саны сияқты роль атқарады.
- Кері матрица
Анықтама Егер АВ= ВА= Е, (Е - бірлік матрица), теңдіктері орындапатындай В матрицасы бар болса, онда ол А матрицсына кері матрица деп аталады да В=А -1 символымен белгіленеді.
Анықтама Анықтауышы нөлге тең емес квадрат матрица нұқсансыз немесе өзгеше емес , ал анықтауышы нөлге тең квадрат матрица нұқсанды немесе өзгеше деп аталады.
Ескерту "Нұқсанды" немесе "нұқсансыз" түсініктері тек квадрат матрицалар үшін ғана қолданылады.
detA-detA -1 = detA⋅A -1 = detE=l
теңдігінен, нұқсанды матрицаның кері матрицасы жоқ екені шығады (өйткені, 0⋅det A -1 ≠1) .
Анықтама
 квадрат матрицасы берілсе, оның
квадрат матрицасы берілсе, оның
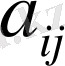 элементтерінің алгебралық
элементтерінің алгебралық
 толықтауыштарынан құралған
толықтауыштарынан құралған
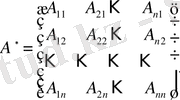
матрицасын қосалқы матрица деп атайды.
Қосалқы матрицаны алу үшін А матрицасының әрбір элементін оның алгебралық толықтауышымен ауыстырып алынған матрицаны транспонирлеу керек.
Қосалқы матрицаның
 Equation. 3
элементінің 1-ші индексі баған, ал 2-ші индексі жол нөмірін көрсетеді.
Equation. 3
элементінің 1-ші индексі баған, ал 2-ші индексі жол нөмірін көрсетеді.
 Equation. 3
элементі
і
-ші баған мен
j
-ші жол қиылысуында тұр.
Equation. 3
элементі
і
-ші баған мен
j
-ші жол қиылысуында тұр.
4-мысал
Егер
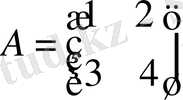 Equation. 3 болса, онда
Equation. 3 болса, онда
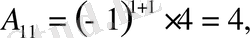
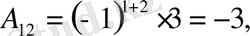
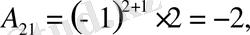
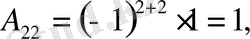
олай болса,
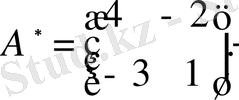
Теорема Нұқсансыз матрицалардың және тек қана солардың кері матрицалары бар, сонымен бірге кері матрица
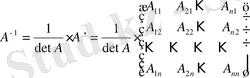 (2)
(2)
формуласы арқылы табылады.
Жоғарыда біз нұқсанды матрица үшін кері матрица болмайтынын дәлелдегенбіз.
Матрица нұқсансыз detА≠0 болсын. Онда

Матрицаларды көбейту ережесі бойынша
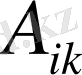 элементтері А* матрицасының
j
-ші бағанында орналасады.
элементтері А* матрицасының
j
-ші бағанында орналасады.
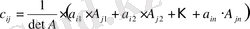
Егер
 болса, онда
болса, онда
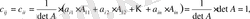
 , ал егер
, ал егер
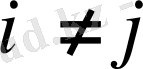 болса. Онда 2. 1. п. 9° бойынша
болса. Онда 2. 1. п. 9° бойынша
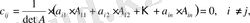
өйткені,
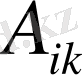 , берілген А матрицасының
j
-ші жол
, берілген А матрицасының
j
-ші жол
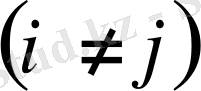 элементтерінің алгебралық толықтауыштары. Сонымен,
элементтерінің алгебралық толықтауыштары. Сонымен,

теңдігі де осылай көрсетіледі.
Олай болса, анықтама бойынша
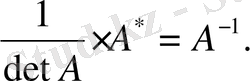
5-мысал
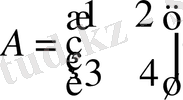 Equation. 3 матрицасына кері матрицаны табу керек.
Equation. 3 матрицасына кері матрицаны табу керек.
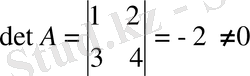 болғандықтан кері матрица бар. Алдыңғы мысалда осы А матрица үшін тіркелген матрицаны тапқан едік:
болғандықтан кері матрица бар. Алдыңғы мысалда осы А матрица үшін тіркелген матрицаны тапқан едік:
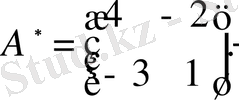 .
.
(2) формула бойынша
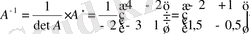
аламыз. Текмерейік:
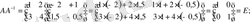
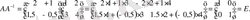
Сонымен,
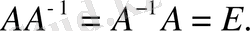 Олай болса,
Олай болса,
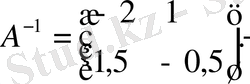
Кepi матрица келесі қасиеттерге ие:
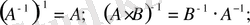
Матрица рангі Тік бұрышты матрицаның сандық сипатын қарастырайық. Матрица рангі базистік жолдар (базистік бағандар) деп аталатын жолдар (бағандар) санын анықтайды, ал қалған жолдарды (бағандарды) осы базистік жолдардың (базистік бағандардың) сызықтық комбинацияларынан алуға болады (27 б. қараңыз) .
Анықтама А матрицасының k-ші ретті миноры дeп А матрицасының кез-келген k жолы мен кез келген k бағандарының қиылысуындағы элементтерінен құралған матрицаны айтады.
Мысалы
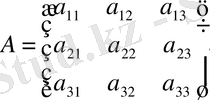 матрицасының бір 3-ші ретті миноры (А матрицасының өзі), тоғыз 2-ші ретті миноры -
матрицасының бір 3-ші ретті миноры (А матрицасының өзі), тоғыз 2-ші ретті миноры -
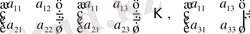
тоғыз 1-ші ретті миноры -
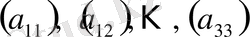
бар.
Басқа бірде бір миноры жоқ.
Анықтама А матрицасының рангі деп осы матрицаның нұқсансыз минорларының ең үлкен ретін айтады және оны r(А) немесе r А немесе rangA символдарының біреуімен белегілейді.
Нөл матрицаның рангі нөлге тең деп есептеледі.
Егер А матрицасы n-ші ретті нұқсансыз (detА≠0) квадрат матрица болса, онда
r(А) =n
; нұқсанды, яғни detA = 0 болса, онда
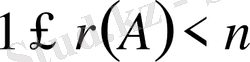 (А - нөлдік матрица емес) ;
(А - нөлдік матрица емес) ;
m×n өлшемді матрица үшін
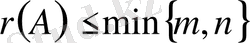 орындалатыны түсінікті.
орындалатыны түсінікті.
Матрица рангін табу үшін оның 1-ші ретті минорынан бастап барлық минорларын нұқсансыздыққа зерттесе болғаны.
Көмкеруші минорлар әдісі бұл процедураны едәуір жеңілдетеді. Осы әдісті түсіндірейік.
Кез-келген 1-ші ретті нұқсансыз минор (А матрицасының нөлге тең емес элементі) алынады, оны А 1 деп белгілейік. Енді А 1 -ді көмкеруші (ішінде А 1 болатын) барлық 2-ші ретті минорлар қарастырылады. Егеp оның барлығы нұқсанды болса, онда r(А) =1 , ал егер ең болмағанда нұқсансыз екінші ретті бір минор бар болса, онда А 2 арқылы белгілейміз. Келесі циклдер осы сияқты жалғасады. А матрицасының k -ші ретті нұқсансыз миноры A k , ал оны көмкеретін барлық минорлар нұқсанды болса, онда r(A) = k, ал егер ең болмағанда нұқсансыз k+1 ретті бір минор бар болса, онда А к+1 нұқсансыз минорын алып процесті одан әрі жалғастырады.
Мысал
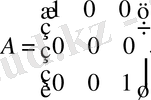 матрицасының рангін табу керек.
матрицасының рангін табу керек.
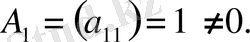 Оны көмкеруші 2-ші ретті минорлар ішінде нұқсансыз минор
Оны көмкеруші 2-ші ретті минорлар ішінде нұқсансыз минор
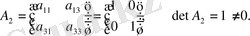
 -ні көмкеруші 3-ші ретті жалғыз минор А матрицасы.
-ні көмкеруші 3-ші ретті жалғыз минор А матрицасы.
Бірақ
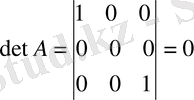 нұқсанды болғандықтан
нұқсанды болғандықтан
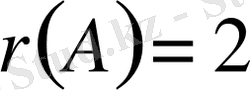 .
.
Матрица рангін табудың тағы бір әдісі - элементар түрлендірулер әдісі, немесе Гаусс әдісі.
Матрицаға жасалған элементар түрлендірулер деп келесі түрлендірулерді айтады.
1. Жолдарды (немесе бағандарды) өзара орын алмастыру;
- Қатарды нөл емес санға көбейту;
- Қатарға оған параллель қатарды қандай да бірkсанына көбейтіп қосу;
- Нөлдік қатарды алып тастау.
Матрицаға жасалған элементар түрлендірулер оның рангін өзгертпейді.
В матрицасы А матрицасынан элементар түрлендрулер арқылы алынса, оларды эквивалент матрицалар деп атайды да А~В арқылы белгілейді
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz