Планиметриядағы көпбұрыштарды оқыту әдістемесі және стандарт емес есептерді шешу тәсілдері


МАЗМҰНЫ
КІРІСПЕ . . .
І КӨПБҰРЫШТАР . . .
1. 1 Үшбұрыш және оның қасиеттері . . .
1. 2 Тіктөртбұрыш, ромб, квадрат және оның қасиеттері . . .
ІІ КӨПБҰРЫШТАРҒА АРНАЛҒАН СТАНДАРТ ЕМЕС ЕСЕПТЕРДІ ШЕШУ ӘДІСТЕМЕЛЕРІ . . .
2. 1 Геометриялық элементтерді оқыту технологиясы . . .
2. 2 Геометрияның планиметрия бөлімі . . .
2. 3 Көпбұрыштарға арналған стандарт емес есептер . . .
ҚОРЫТЫНДЫ . . .
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ . . .
КІРІСПЕ
Тақырыптың өзектілігі: Ғылым мен техниканың қарқынды дамуы және әлеуметтік экономикалық өзгерістер жас ұрпақты тәрбиелеуге жаңаша көзқараспен қарауды талап етуде. Бұл әрбір адамның психикалық, жеке тұлғалық қасиеттерін дамытуға мүмкіндік беретін жаңа жағдайлар құруды қажет етеді.
Осыған байланысты қазіргі педагогика ғылымы оқушылардан белгілі бір білім жүйесін терең меңгеруін талап етіп қана қоймастан, олардың әрқайсысының шығармашылық қабілетін дамытуды талап етіп отыр. Оқушылардың өздігінен есеп шығаруын дербестендіру олардың білімі мен іскерліктеріндегі олқылықтарды анықтауға жағдай жасайды. Ол үшін математиканың негізгі бөлімдерінің бірі төртбұрыштарды оқытудың тиімді әдістерін қарастырған жөн.
Оқушылардың жоғары математикалық мәдениетін қалыптастырудың негізгі жолы - әр түрлі есептерді шығару кезінде ұйымдастыра білу.
Оқушылардың математикалық ой-өрісінің дамуы, олардың есеп шығара білуінен анық байқалатыны рас. Қиын да, қызықты есептерді шығара білу - оқушылардан талмас еңбекті, зор күш пен табандылықты қажет етеді. Міне, осындай қасиеттердің барлығы да оқушылардың бойында есепке деген ынтасы оянғанда ғана күшейе және арта түседі.
Оқушылардың математикалық ойлау қабілетін арттырудың ең тиімді тәсілі - оларды анализ және синтез, салыстыру және ұқсастыру т. б. арқылы маңызды тәсілдермен қаруландыру болып табылады. Сондай тәсілдердің бірі - стандарт (үйреншікті) есептер мен стандарт емес есептерді салыстыра отырып шешу болып табылады.
Стандарт емес есептер оқушылардың ойлау қабілетін дамытады, ойлауға жетелейді және де есепке деген ынтасын, қызығушылығын арттырады.
Стандарт емес есептер оқушылардың үйреншікті жолмен шығара салуына мүмкіндік бермейді. Демек, стандарт емес есептер оқушылардың математикалық ойлау қабілетін дамытудың негізгі құралы болып табылады.
Жұмыстың мақсаты: Қазіргі уақытта оқу орындарының негізгі міндеттерінің бірі - оқушылардың шығармашылық ойлау қабілеттерін анықтау және оларды дамыту проблемаларын шешу болып табылады.
Үшбұрыш және оның қасиеттері мен түрлерінің қолданылуын жан-жақты қарастыру болып табылады. Дипломдық жұмыста негізгі қамтылған мәселелер де осы көпбұрыштардың қолданысы, ``Көпбұрыш`` тақырыбын мектепте оқыту әдістемесі мен оның өмірдегі маңызы және тарихына шолу жасау болып табылады.
Жұмыстың міндеті:
- Тақырып бойынша теориялық мағлұматтарды жинақтау,
- Мектеп математикасы курсында көпбұрыш тақырыбының қарастырылуына әдістемелік талдау жасау;
- Cтандарт емес есептер оқушылардың математикалық ойлау қабілетін дамытудың негізгі құралы;
- Оқушылардың көпбұрыштарға қатысты есептерді шешуде білім-дағдыларын қалыптастырудың әдістемелік жүйесін құру.
Дипломдық жұмыстың құрылымы мен мазмұны : Бұл дипломдық жұмыс IV бөлімнен тұрады. Олар кіріспе, негізгі бөлім, қорытынды және пайдаланылған әдебиеттер тізімі. Негізгі бөлімде мынандай мәселелер қарастырылады:
1) Көпбұрыштар туралы түсінік.
2) Көпбұрыштарға арналған стандарт емес есептерді шешу әдістемелері.
3) Геометриялық элементтерді оқыту технологиясы.
І КӨПБҰРЫШТАР
1. 1 Үшбұрыш және оның қасиеттері.
Үшбұрыш - ең қарапайым көпбұрыш, үш нүктеден, үш қабырғадан және үш бұрыштан тұрады немесе бір түзу бойында жатпайтын үш нүктені қосатын кесінділер шектейтін жазықтық бөлігі.
Үшбұрыштың биіктігі деп - үшбұрыштың төбесін сол төбеге қарсы жатқан қабырғамен қосатын перпендикуляр кесінді аталады.
Биіктіктердің қасиеттері:
- Үш биіктік (немесе олардың созындылары) бір нүктеде қиылысады, ол нүкте үшбұрыштың ортоцентрі деп аталады.
А) сүйір бұрышты үшбұрыш
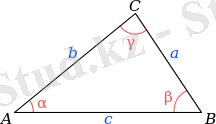
Ә) тікбұрышты үшбұрыш
Б) доғал бұрышты үшбұрыш
2) Биіктік ұзындығы :
;
, мұндағы
b c
a
- Үшбұрыштың биіктіктері оның қабырғаларына кері пропорционалды:
Мысал: Үшбұрыш қабырғалары берілген: а=15, в=16, с=17. Кіші қабырғасына түсірілген биіктікті табыңыз.
Шешуі: Кіші қабырғасы a=15 екені анық. Онда,
24
Жауабы:
Үшбұрыштың орта сызығы деп - үшбұрыштың екі қабырғасының ортасын қосатын кесіндіні айтады.
Орта сызықтардың қасиеттері :
1) Үшбұрыштың екі қабырғасының ортасын қосатын орта сызық үшінші қабырғаға параллель және оның жартысына тең болады:
МN АС ; МN= AC
B
M N
A C
2) Үшбұрыштың үш орта сызығы оған ұқсас болатын тең 4 үшбұрышқа бөледі, ұқсастық коэффициенті -ге тең.
Үшбұрышка арналған есептер:
1. Қабырғалары 17 см, 65 см және 80 см тең болатын үшбұрыштың ең кіші биіктігін табыңыз.
Шешімі: ең кіші биіктік үлкен қабырғаға жүргізілген
ah= ;
Мұндағы: :
h = ; р = ; h = = 7, 2
Жауабы:7, 2 см .
2. Егер тікбұрышты үшбұрыштың тік бұрышынан гипотенузаға түсірілген биіктігі оны 3 см және 27 см бөліктерге бөлетін болса, онда осы биіктіктің ұзындығы қандай ?
Шешімі:тік бұрышты үшбұрышта геометриялық орта мәнді қолданамыз:
С
А D B
CD 2 =AD*DB= 3*27=81;
h=CD= =9
Жауабы: 9 см.
3. АВС үшбұрышы төбелерінің координаттарымен берілген :А(1; 2) , В(2; -2) , С(6; 1) . СD биіктігінің теңдеуін құрастырамыз.
А(1; 2) С(6; 1)
D
В(2; -2)
Шешімі:
AB түзуінің теңдеуі :
y= -4х+6.
АВ CD, k 1 *k 2 =-1 .
k * (-4) =-1 ; k= .
Бұрыштық коэффициенті k түзуінің теңдеуі :
y=y 0 +k(х-х 0 ) ,
у= 1+ (х-6) .
Жауабы: х-4y -2 = 0 .
4. Қабырғасы а болатын тең қабырғалы үшбұрыштың биіктігін табыңдар .
Шешімі:
h= =
а а h=
а
Жауабы: .
5. Теңбүйірлі тікбұрышты үшбұрышқа іштей сызылған шеңбердің радиусы мен гипотенузаға жүргізілген биіктіктің қатынасын табыңыз.
С
А В
Шешуі:
Қосымша элемент енгізейік, теңбүйірлі тікбұрышты үшбұрыштың катеті х . Онда :АС=СВ =х, АВ=х .
СН = = (гипотенузаға түсірілген биіктік сырттай сызылған шеңбер радиусына және гипотенузаның жартысына тең ) .
Үшбұрышқа іштей сызылған шеңбердің радиусы : r = .
r = OH = =
= = = -1
Жауабы: -1.
Дұрыс үшбұрыш
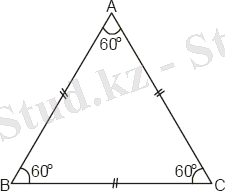
Дұрыс (немесе тең қабырғалы) үшбұрыш - бұл үш қабырғасы бар дұрыс көпбұрыш, дұрыс көпбұрыштардың ішіндегі алғашқысы. Дұрыс үшбұрыштың барлық қабырғалары өзара тең, ал барлық бұрыштары 60° тең. Тең қабырғалы үшбұрышта биіктігі үшбұрыштың биссектрисасы және медианасы болып табылады.
Қасиеттері:
Барлық бұрыштары тең.
Әрбір медиана сол бұрыштан жүргізілген биіктікпен және биссектрисамен беттесі.
Іштей және сырттай сызылған шеңберлердің центрлары беттеседі.
Дұрыс үшбұрыш.
Дұрыс тетраэдрдің бүйір жақтары - дұрыс үшбұрыш.
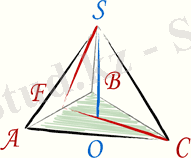
а - дұрыс үшбұрыштың қабырғасы,
R - сырттай сызылған шеңбердің радиусы,
r - іштей сызылған шеңбердің радиусы.
Дұрыс үшбұрышқа сырттай сызылған шеңбердің радиусын қабырғасы арқылы өрнектеу:
Дұрыс үшбұрышқа іштей сызылған шеңбердің радиусын қабырғасы арқылы өрнектеу:
Дұрыс үшбұрыштың периметрі:
Дұрыс үшбұрыштың биіктігі, медианасы және биссектрисасы:
Дұрыс үшбұрыштың ауданы келесі формуламен есептеледі:
Сырттай сызылған шеңбердің радиусы іштей сызылған шеңбердің екі есесіне тең:
Есептер:
Дұрыс үшбұрыштың периметрі см. Оған іштей сызылған шеңбердің ұзындығын табыңыз.
Берілгені:
C-?
Шешуі:
Жауабы:
Дұрыс үшбұрышқа қабырғасы m болатын квадрат іштей сызылған. Үшбұрыш қабырғасын табыңыз.
Берілгені:
Жауабы:
Теңқабырғалы үшбұрыштың медианасы см-ге тең. Үшбұрыш периметрін табыңыз.
Берілгені:
P-?
Шешуі:
Жауабы: 90
Дұрыс үшбұрыштың ауданы
Берілгені:
Шешуі:
Жауабы: 1
Дұрыс үшбұрышқа сырттай сызылған шеңбердің радиусы 24 см тең.
Үшбұрышқа іштей сызылған шеңбердің радиусын табыңыз.
Берілгені:
r-?
Шешуі:
,
Жауабы:
Үшбұрышқа іштей сызылған шеңбердің радиусы
Ауданын табыңыз.
Берілгені:
S-?
Шешуі:
Жауабы:
Төртбұрыш - төрт нүктеден және оларды тізбектей қосатын төрт кесіндіден тұратын фигура.
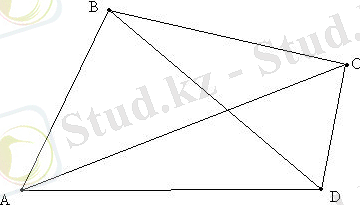
АВ мен ВС, ВС мен СД, СД мен АД, АД мен АВ кесінділері бір түзудің бойында жатпайды;
АВ мен СД, ВС мен АД кесінділері бір-бірімен қиылыспайды;
А, В, С, Д нүктелері төртбұрыштың төбелері;
А мен В, В мен С, С мен Д, Д мен А - көршілес төбелері;
В мен Д, С мен А қарсы төбелері;
АВ, ВС, СД, ДА кесінділері - төртбұрыштың қабырғалары;
АВ мен ВС, ВС мен СД, СД мен ДА, ДА мен АВ кесінділері - көршілес қабырғалары;
АВ мен СД, ВС мен АД - қарама-қарсы қабырғалары;
АС мен ВД кесінділері - диагональдар;
 АВС,
АВС,
 ВСД,
ВСД,
 СДА,
СДА,
 ДАВ - төртбұрыштың бұрыштары;
ДАВ - төртбұрыштың бұрыштары;
Р=АВ + ВС + СД + ДА периметрі;
АВСД, ВСДА, СДАВ, ДАВС - төртбұрыштың белгіленуі
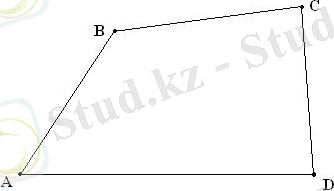
Қабырғасын қамтитын әр түзумен шектелген жарты жазықтықтың тек біреуінде ғана жатса, дөңес төртбұрыш болады.
Егер төртбұрыштың диогональдары қиылысса, төртбұрыш дөңес болады.
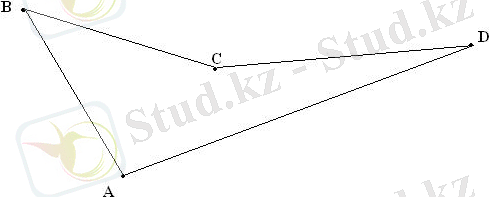
Төртбұрыш қабырғасын қамтитын кемінде бір түзумен шектелген жарты жазықтықтардың екеуінде де жатса, дөңес емес төртбұрыш болады.
Егер төртбұрыштың диогональдары қиылыспаса, төртбұрыш дөңес емес болады.
Параллелограмм - қарама-қарсы қабырғалары параллель болатын, яғни параллель түзулердің бойында орналасқан төртбұрыш.
«Параллелограмм» грек сөзі. Проклдың жазуынша, оны Евклид енгізген. Параллелограмм түсінігі және параллелограмның кейбір қасиеттері пифагорлықтарға да белгілі болған. Евклидтің «Бастамаларында» мына теорема дәлелденген: «Параллелограмның қарама-қарсы қабырғалары және қарама-қарсы бұрыштары тең, ал диагоналі оны тең екі бөлікке бөледі». Параллелограмдардың толық теориясы орта ғасырлардың аяғына қарай талданып, XVII ғасыр оқулықтарында көрініс тапты. Параллелограмдар туралы теоремалардың бәрі де тікелей немесе жанама түрде Евклидтің параллельдік аксиомасына негізделген.
Параллелограммның қасиеттері:
Қарама - қарсы қабырғалары тең:
Қарсы жатқан бұрыштары тең:
Диагональдары қиылысады және қиылысу нүктесінде қақ бөлінеді.
Бұрыштарының іргелес біржақты жатқан қабырғаларының қосындысы:
180º-қа тең.
Диагональдарының квадраттарының қосындысы оның барлық қабырғаларының квадраттарының қосындысына тең.
Параллелограммның белгілері:
Егер мына шарттар орындалса онда төртбұрыш параллелограмм болады:
Қарама - қарсы қабырғалары тең және параллель (AB = CD, AD = BC)
Қарама - қарсы қабырғалары қос - қостан тең (AB = CD, AB CD) .
Қарама - қарсы бұрыштары қос - қостан тең (∠A = ∠C, ∠B = ∠D) .
Диагональдары қиылысу нүктесінде қақ бөлінеді (AO = OC, BO = OD) .
Параллелограмм дегеніміз - қарама-қарсы қабырғалары қос-қостан параллель, яғни параллель түзулер бойында жататын төртбұрыш.
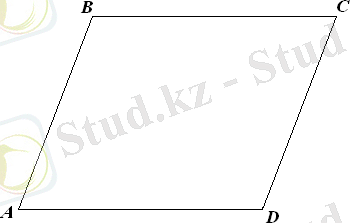
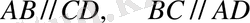
Параллелограмның бір төбесінен қарсы жатқан қабырғасына түсірілген перпендикуляр оның биіктігі деп, ал биіктік түсірілген қабырға табаны деп аталады.
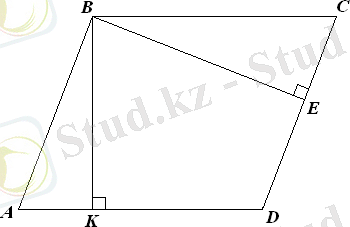
 .
.
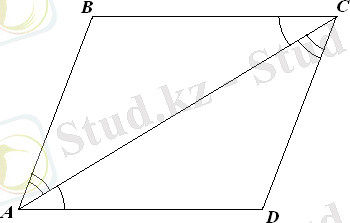 1 қасиет.
Параллелограмның қарама-қарсы қабырғалары тең.
1 қасиет.
Параллелограмның қарама-қарсы қабырғалары тең.
Берілгені: АВСД - параллелограмм
Дәлелледеу керек: АВ = СД, ВС = АД
Дәлелдеуі:
ВС//АД, АС қиюшы болған ішкі айқыш бұрыштар
 ДАС =
ДАС =
 ВСА ; АВ//ДС; А қиюшы ішкі айқыш бұрыштар
ВСА ; АВ//ДС; А қиюшы ішкі айқыш бұрыштар
 ДСА=
ДСА=
 ВАС, ал АС ортақ қабырға, онда үшбұрыштар теңдігінің II белгісі бойынша
ВАС, ал АС ортақ қабырға, онда үшбұрыштар теңдігінің II белгісі бойынша
 , бұдан АВ = ДС. ВС = АД теорема дәлелденді.
, бұдан АВ = ДС. ВС = АД теорема дәлелденді.
2 қасиет. Параллелограмның диагоналі оны өзара тең екі үшбұрышқа бөледі.
3 қасиет. Параллелограмның қарама-қарсы бұрыштары тең.
Бұл қасиеттің дәлелдеуі
 деп шығады.
деп шығады.
4 қасиет. Параллелограмның диагональдары қиылысу нүктесінде тең екі бөлікке бөлінеді.
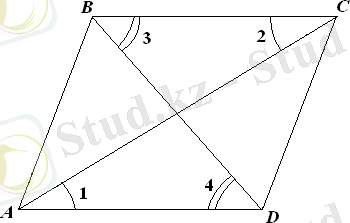 Берілгені
:: параллелограмм,
Берілгені
:: параллелограмм,
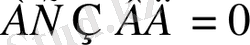
Дәлелдеу керек:
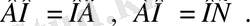
Дәлелдеуі:
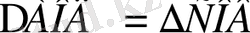 себебі
себебі
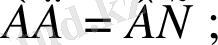
 1=
1=
 2,
2,
 3=
3=
 4 ішкі айқыш бұрыштар болғандықтан, онда үшбұрыштарды қалған сәйкес қабырғалары да тең болады ВО=ОД; АО=ОС .
4 ішкі айқыш бұрыштар болғандықтан, онда үшбұрыштарды қалған сәйкес қабырғалары да тең болады ВО=ОД; АО=ОС .
5 қасиет. Параллелограмның бір қабырғасына іргелес бұрыштарының қосындысы 180º-қа тең.
Бұл қасиеті екі параллель түзуді үшінші түзумен қиғанда пайда болған тұстас бұрыштардың қосындысы 180º-қа тең деген түзулердегі параллельдік белгісінен шығады.
Есептер:
1)
 Берілгені:
ABCD параллелограмм
Берілгені:
ABCD параллелограмм
AB+AD=12см
AB:AD=1:2
Т/к: AB, AD-?
Шешуі: AB=x, AD=2x
x+2x=12 x=4
AB=4см, AD=8 см
Жауабы: 4 см, 8 см
2)
 Берілені:
ABCD параллелограмм
Берілені:
ABCD параллелограмм
<А < <В
<А=<B - 7 0 30 '
Т/к: <A, <B, <C, <D - ?
Шешуі: <А+<В=180 0
<B - 7 0 30 ' +<B=180 0
2 <B=187 0 30 '
< B=93 0 45'
<A=93 0 45' - 7 0 30 ' =86 0 15'
Жауабы: <A=<C=86 0 15'
<B=<D=93 0 45'
3) Параллелограмның екі қабырғасының қосындысы 12 см, ал олардың қатынасы 3:2. Параллелограмның қабырғаларын тап.
 Берілгені:
ABCD - параллелограмм
Берілгені:
ABCD - параллелограмм
AD:AB=3:2
AD+AB=12 см
Т/к: AB, AD-?
Шешуі: AD=3x. AB=2x
3x+2x=12
5x=12
x=2, 4
AB=2∙2. 4=4. 8 см, AD=3∙2. 4=7. 2 см
Жауабы: 4, 8см, 7, 2 см.
1. 2 Тіктөртбұрыш, ромб, квадрат және оның қасиеттері.
Барлық бұрыштары тік болатын параллелограмды тіктөртбұрыш деп атайды. Анықтамадан тіктөртбұрыш параллелограмның дербес жағдайы екені белгілі, олай болса параллелограмның барлық қасиеттері тіктөртбұрыштың қасиеттері болады. Онда «параллелограмм» сөзінің орнына «тіктөртбұрыш» деп қойып қасиеттерін айтып шығыңдар.
1-қасиет: Тіктөртбұрыштың қарама-қарсы қабырғалары тең
2-қасиет: Диагональдары оны тең екі үшбұрышқа бөледі
3-қасиет: Диагональдары қиылысу нүктесінде тең екіге бөлінеді.
4-қасиет: Бір бұрышының биссектрисасы тең бүйір үшбұрыш түзеді.
Осы қасиеттерден басқа тіктөртбұрышқа тән қасиеттер:
«Тіктөртбұрыштың диагональдары тең болады. »
В С Берілген:
АВСД- тіктөртбұрыш
Д/К : АС=ВД
Дәлелдеу: ΔВАД мен ΔСДА
қарастырамыз.
А Д
Бұл тік бұрышты үшбұрыштарды <А=<Д=90 0
АВ=ДС. АД-ортақ. Екі катеті бойынша ΔВАД мен ΔСДА. Онда оның қалған элементтері де тең, гипотенузалары ВД=АС: бізге дәлелдеу керегі де осы еді.
Тік төртбұрыштың белгілері:
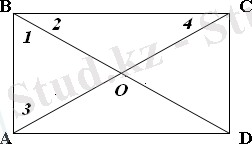 1 белгісі: Егер параллелограмның диагональдары тең болса, онда ол тіктөртбұрыш болады.
1 белгісі: Егер параллелограмның диагональдары тең болса, онда ол тіктөртбұрыш болады.
Берілгені: АВСД параллелограмм
АС=ВД
Дәлелдеу керек:
 А=
А=
 В=
В=
 С=
С=

 =90
0
=90
0
Дәлеледеу:
АС=
 - шарт бойынша, параллелограмм қасиеттері бойынша АО=ОС, ВО=
- шарт бойынша, параллелограмм қасиеттері бойынша АО=ОС, ВО=
 , АО=ОС=ВО. ΔВОС, ΔАОВ- теңбүйірлі үшбұрыштар, бұдан <2=<4. <1=<3. Ал ΔАВС- ның ішкі бұрыштарының қосындысы <3+<1+<2+<4=180
0
, АО=ОС=ВО. ΔВОС, ΔАОВ- теңбүйірлі үшбұрыштар, бұдан <2=<4. <1=<3. Ал ΔАВС- ның ішкі бұрыштарының қосындысы <3+<1+<2+<4=180
0
2 (<1+<2) =180 0
<1+<2=90 0 <АВС=90 0
Онда
 А=
А=
 В=
В=
 С=
С=

 =90
0
теорема дәлелденді.
=90
0
теорема дәлелденді.
2 белгісі: Егер параллелограмның бір бұрышы тік болса, онда ол тіктөртбұрыш болады.
3 белгісі: Егер төртбұрыштың үш бұрышы тік болса, онда ол тік төртбұрыш болады.
Тіктөртбұрыштың төбелері арқылы өтетін шеңбер болады. Оның центрі диагоналдардың қиылысу нүктесі болады.
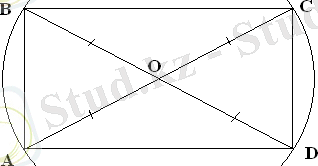
R=
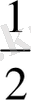 АС=
АС=
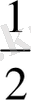 ВД Р=2 (АВ+АД)
ВД Р=2 (АВ+АД)
Есептер:
 1)
1)
Берілгені: АВСД тіктөртбұрыш
АВ=(АД-2, 5) м
Т/К: Р=?
Шешуі: Р=2 (АВ+АД)
АВ=15-2, 5=12, 5м
Р=2 (15-2, 5) =2∙27, 5=55
Жауабы: 55м
2)
В С Берілгені: АВСД тіктөртбұрыш
Р=24 м
АВесе қысқа
АД
А Д Т/К: АВ, АД
Шешуі: АВ=х деп белгілесек АД=2х Р=2(АВ+АД)
12 =3х
х=4
АВ=4м. АД=8м
Жауабы: 4м, 8м
3)
Берілгені:
АД-АВ=3 дм
АД:АВ=5:3
Т/К: АВ, АД-?
Шешуі: АД=5х, АВ=3х
5х-3х=3
2х=3
х=1, 5
АД=5∙1, 5=7, 5 АВ=4, 5
Жауабы: 7, 5м, 4, 5 м
Анықтама: Барлық қабырғалары тең параллелограмм ромб деп аталады.
A
B
C
D
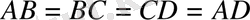
Ромб деген сөйлем параллеллограмның дербес түрі болғандықтан параллелограмның барлық қасиеттері ромбының қасиеттері болады.
Оқушыларға сұрақ қойып ромбының қасиеттерін айтқызу.
Ромбының қарама - қарсы бұрыштары тең.
Ромбының бір қабырғасына іргелес бұрыштарының қосындысы 180 0 қа тең.
Ромбының диагональдары қиылысу нүктесінде тең екіге бөлінеді.
Ромбының диагональі оны өзара тең екі үшбұрышқа бөледі
Теорема: Ромбының диагональдары тік бұрыш жасап қиылысады. Ромбының диагональдары оның бұрыштарының биссекрисалары болады.
A
B
C
D
O
Берілгені : АВСД ромб
Дәлелдеу керек :

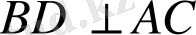
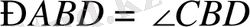
Дәлелдеу:
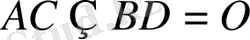
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz