Гейзенбергтің анықтамалмағандық қағидасы

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 3 бет
Таңдаулыға:

Гейзенбергтің анықтамалмағандық қағидасы .

Гейзенбергтің анықталмаушылық принципі

Зат бөлшектерінің толқындық және корпускулалық екі жақты табиғаты - кез келген ұсақ бөлшектерді әрі жарықтың толқындық, әрі фотонның кванттық теориясымен сипаттауға мүмкіншілік береді. Олай болса көзге көрінбейтін микродүние ішіндегі бөлшектердің табиғатын зерттеу үшін классикалық физика ұғымдарын қолданудың мүмкіншілігі болар ма екен деген заңды сұрақ туады.

Классикалық механикада қозғалатын кез келген материалдық нүктенің белгілі бір траекториясы болады және кез келген уақытта оның координаты мен импульсін анықтауға болады. Ал көзге көрінбейтін ұсақ бөлшектері болса (микробөлшектер), өзінің толқындық қасиеті болу себебінен классикалық бөлшектерден ерекше айырмашылығы болады. Микробөлшектердің негізгі айырмашылығы олардың траекториясы болмайды, сондықтан да бір мезгілде бөлшектің координаты мен импульсін дәл өлшеудің мүмкіншілігі жоқ. Олай болса микробөлшектерді макробөлшектерге тән физикалық шамаларымен тек жуықтап қана сипаттауға болады. Осы пікірге байланысты толқындық механикада мынадай принцип бар: электронның (немесе кез келген ұсақ бөлшектердің) орнын және импульсін бір мезгілде дәл өлшеу мүмкін емес. Мысалы, фотонның осі бойынша координатын өлшегендегі қателік болып, оның жылдамдығын өлшеудегі қателік 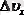болса, онда осы пен 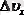көбейтіндісінің шамасы 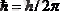тұрақтысынан, яғни Планк

тұрақтысынан кем болмайды: 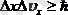немесе 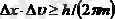. Бұл теңсіздікті басқаша жазып көрсетейік;

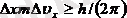http://lib.kstu.kz:8300/tb/books/2015/Fizika/Huanbay%20i%20dr/teory/2.1.files/image015.gif

немесе

http://lib.kstu.kz:8300/tb/books/2015/Fizika/Huanbay%20i%20dr/teory/2.1.files/image017.gif

мұндағы 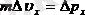- импульсті өлшеудегі қателік, - бөлшектер массасы, 2. 5 теңсіздікті басқа координаттар үшін де жазуға болады, яғни:

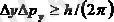http://lib.kstu.kz:8300/tb/books/2015/Fizika/Huanbay%20i%20dr/teory/2.1.files/image023.gif

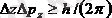http://lib.kstu.kz:8300/tb/books/2015/Fizika/Huanbay%20i%20dr/teory/2.1.files/image025.gif

Осы 2. 5 және 2. 6 теңсіздіктерін бірінші рет 1927 ж. неміс физигі В. Гейзенберг (1901-1976) ұсынған болатын, сондықтан бұлар Гейзенбергтің анықталмаушылық теңсіздіктері деп аталады. Осы қатыстардың физикалық мәнін түсіндірейік.

Егер де координат мәні, яғни -тің мәні дәл өлшенсе, онда импульстің белгілі бір мәні болмайды.

Себебі 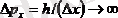ұмтылады. Ал импульстің мәні дәл өлшенсе, онда координаттың белгілі бір мәні болмайды, себебі 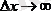ұмтылады.

Сөйтіп ғылыми материалистік тұрғыдан қарағанда траекторияның, координаттың, жылдамдықтың белгілі бір шектері бар болатындықтан, олар материяның ерекше қасиеттерін сипаттай алмайды.

Гейзенбергтің анықталмаушылық теңсіздіктеріндегі Планк тұрақтысы өте аз шама болғандықтан координаттар мен жылдамдықтың анықталмаушылығы тек элементар бөлшектерде ғана анық білінеді де, ірі бөлшектерде байқалмайды.

Енді анықталмаушылық принципті кейбір мысалдарға қолданайық. Мысалы, атомның ішінде қозғалатын электронды қарастырайық, яғни оның координатын анықтамақ болайық. Сонда электронның орны 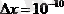м дәлдікпен анықталуы керек, бұл негізгі күйіндегі атомның радиусымен шамалас ( м) . Олай болса, электронның жылдамдығын анықтағанда кететін қателік (12) қатынас бойынша мынаған тең болады:

м/с.

Сөйтіп, атомның ішіндегі электрон жылдамдығының шамасы м/с екен. Сонда атом ішіндегі электрон жылдамдығын анықтаудағы қате сол жылдамдықтың өзіне тең болып отыр. Сондықтан атомның ішінде электрон белгілі бір жылдамдықпен қозғалатын тұйықталған орбитасы бар деуіміз дұрыс емес.

Атом ішіндегі электронның орны мен жылдамдығын бір мезгілде дәл анықтауға болғанымен, оның атомның ішінде берілген нүктеде болу ықтималдығын анықтауға болады. Осы ықтималдық берілген нүктедегі электр зарядының ұзақ уақыттағы орташа тығыздығын сипаттайды. Сөйтіп, электрон бір орнында неғұрлым жиі болып тұрса, оның заряды көп болады да, ал сирек болған орнының заряды аз болады.

Сонымен қатар, кванттық теорияның негізінде уақыт пен энергияның анықталмаушылық қатыстары да қарастырылады, яғни

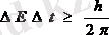http://lib.kstu.kz:8300/tb/books/2015/Fizika/Huanbay%20i%20dr/teory/2.1.files/image042.gif

Сонда белгілі бір жүйенің орташа өмір сүру уақыты болса, онда оны сипаттайтын энергияны дәл өлшеу мүмкін емес. Сол сияқты энергияның белгілі бір мәні болса, онда керісінше уақытты өлшеуде қателіктердің болуы ақиқат. Бұл тәжірибеден спектрлік сызықтардың енділігін өлшей отырып, атомның қозу күйіндегі өмір сүру уақытын білуге болады.

Гейзенбергтің анықталмаушылық қатыстары көптеген ғалымдар арасында, әсіресе буржуазиялық философ талқылауында идеалистік көзқарастар басым болды. Олардың пікірінше, егер зат бөлшектерінің координаттары мен импульсін діл анықтау мүмкін болмаса онда бұл пікірді дүние тануға қолданудың шегі де болмауы керек деді, сонымен қатар кеңістік пен уақытқа байланыссыз микродүниенің өмір сүруі де мүмкін емес.

Ал шын мәнінде, анықталмаушылық қатыстарды біз микродүниенің шегін тану үшін емес, тек классикалық механиканың осы пікірге қолданудың мүмкіндігін ғана көрсетеміз.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.