Stud.kz

Математикалық физика теңдеулері және оларды канондық түрге келтіру


Жұмыс түрі:  Курстық жұмыс
Тегін:  Антиплагиат
Көлемі: 17 бет
Таңдаулыға:   

Ө. Сұлтанғазин атындағы Қостанай мемлекеттік педагогикалық университеті

Жаратылыстану-математика факультеті

Физика-математикалық пәндер кафедрасы

КУРСТЫҚ ЖҰМЫС

Математикалық физиканың негізгі теңдеулері, оларды сыныптау және канондық түрге келтіру

5В011000-Физика

Орындаған: Абдисаматова Г. М.

Ғылыми жетекшісі: Касымова А. Г.

Қостанай 2019

МАЗМҰНЫ

Кіріспе . . . . .
3
Кіріспе . . . . .: 1 Математикалық физика теңдеулері және оларды канондық түрге келтіру . . .
3: 4
Кіріспе . . . . .: 1. 1 Екінші ретті дербес туындылы дифференциалдық теңдеулер. Екінші ретті теңдеулерді сыныптау . . .
3: 4
Кіріспе . . . . .: 1. 2 Теңдеулерді түрлендіру және канондық түрге келтіру . . .
3: 7
Кіріспе . . . . .: 1. 3 Канондық түрге келтіру әдісі сипаттауыштар әдісі . . .
3: 9
Кіріспе . . . . .: 2 Практикалық бөлім . . .
3: 11
Кіріспе . . . . .: 2. 1 Есептерді шығару мысалдары . . .
3: 11
Кіріспе . . . . .: 2. 2 Тақырып бойынша өзіндік жұмыстарға арналған тапсырмалар . . .
3: 18
Кіріспе . . . . .: 2. 3 Тақырып бойынша бақылау сұрақтар . . .
3: 19
Кіріспе . . . . .: Қорытынды . .
3: 21
Кіріспе . . . . .: Пайдаланылған әдебиеттер . . .
3: 22

КІРІСПЕ

Бізді қоршаған орта немесе біздің барлық көретініміз, сезінетініміз және еститінімміз дербес туындылы диффеенциалдық теңдеулер немесе қысқаша айтқанда, математикалық физиканың теңдеулері ақылы сипатталады деп толық сеніммен айтуға болады.

Тарихи тұрғыдан алғанда, оның негізінде дебес туындылы диффенциалдық теңдеулер жататын математикалық модельдің көпшілігі гидрдинамика, аэродинамика және эдектродинамикадағы физикалық процестерді сипаттайтын есептерді шешу үшін құрылған. Сондықтан да, дербес туындылы диффеенциалдық теңдеулер, сонымен қатар, математикалық физиканың теңдеулері деген атқа ие болды.

Қазіргі кезде осы сияқты теңдеулердің көмегімен әртүрлі, мысалы: физикалық, химиялық, биологиялық, экологиялық, экономикалық, т. с. с. табиғи құбылыстар үлгіленеді.

Осымен байланысты, бір қарағанда әртүрлі құбылыстарды, мысалы, жылудың тұтас ортада таралуын, химиялық бөлшектердің диффузиясын, магниттік өрістің жақсы өткізетін ортаға сіңуін және эпидемия толқындарының таралуын, т. с. с. бірдей теңдеулермен сипаттауға болады.

Осыдан математикалық физика теңдеулері қазіргі кезде математиканың үлкен және іс жүзінде, терең облысын құрайтыны ғажап емес.

Қурстық жұмыстың тақырыбы: Математикалық физиканың негізгі теңдеулері, оларды сыныптау және канондық түрге келтіру.

Мақсаты: Математикалық физика теориясының іргелі ұғымдарымен таныстыру, қойылған есептерде шығара білу қабілетін арттыру.

Міндеттері

  • әдебиеттерді зерттеу,
  • тақырып бойынша есептер шығару үлгілерін келтіру,
  • өзіндік тапсырмалар құрастыру.

Курстық жұмыстың құрылымы: кіріспе, екі тараудан, қорытындыдан және әдебиеттер тізімінен тұрады

1 Математикалық физика теңдеулері және оларды канондық түрге келтіру

1. 1 Екінші ретті дербес туындылы дифференциалдық теңдеулер. Екінші ретті теңдеулерді сыныптау

Жалпы жағдайда 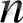тәуелсіз айнамалының 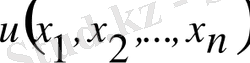белгісіз функциясын және оның дербес туындыларын байланыстыратын дифференциалдық теңдеуді

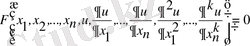(1. 1)

түрінде жазуға болады.

Теңдеудің құрамына кіретін туындылардың ең жоғарғы ретін теңдеудің реті деп атайды. Теңдеуді қанағаттандыратын кез келген дифференциалданатын

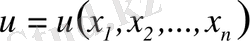
функциясы теңдеудің шешімі деп аталады.

Механиканың және физиканың көптеген есептері екінші ретті дербес туындылы дифференциалдық теңдеулерді зерттеуге әкеледі. Сондықтан біз екінші ретті дербес туындылы теңдеулерді ғана қарастырамыз.

Егер теңдеудің құрамына белгісіз функция және оның туындылары сызықты түрде кіретін болса, онда ол сызықтық теңдеу деп аталады.

Ал егер теңдеу оның құрамындағы жоғары ретті туындылары бойынша ғана сызықты болса, онда ол сызықтылау (квазисызықты ) теңдеу деп аталады.

Оны былай жазуға болады:

(1. 2)

∂

(

)

∑

1

=

∂

∂

∂

і ∂

∂

∂

n

j

i

0

=

х n

u

х 1

u

, . . . ,

,

х 1 , . . . х n, u,

f

+

yj

x

u

n

x

, . . . ,

1

x

ij

a

2

,

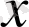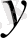Бұл теңдеу екі және тәуелсіз айнымалылары үшін мына түрде жазылады:

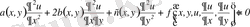(1. 3)

Дербес туындылар үшін төмендегідей де белгілеулерді пайдаланады:

, , , , ,

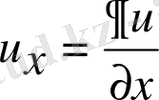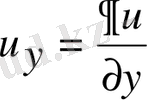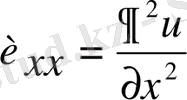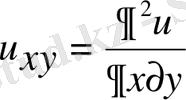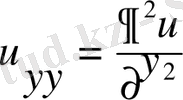т. с. с.

Осы белгілеулерді пайдаланып (1. 3) теңдеуді былай жазуға болады:

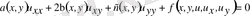(1. 3 / )

Егер (1. 3 / ) теңдеу жоғары ретті 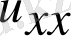, , 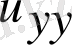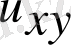дербес туындылары бойынша ғана емес, сонымен қатар белгісіз функциясы мен оның бірінші ретті 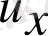және 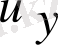туындылары бойынша да сызықты болса, онда ол сызықты теңдеу болады.

Бұл жағдайда (1. 3) теңдеу мына түрде жазылады:

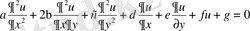(1. 4)

Мұндағы 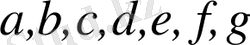- 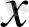және 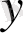тәуелсіз айнымалыларының функциялары. Егер (1. 4) теңдеуінің коэффициенттері 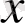пен 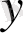ке тәуелді болмаса, онда ол теңдеу коэффициенттері тұрақты сызықтық теңдеу деп аталады. Ал егер 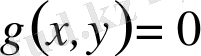болса, онда (1. 4) теңдеу біртекті сызықтық теңдеу деп аталады.

Төмендегі екінші ретті теңдеулер математикалық физиканың негізгі теңдеулері деп аталады:

1) толқындық теңдеу

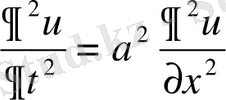
мұндай теңдеуді зерттеуге шектің көлденең тербелістері, стерженнің бойымен тарайтын тербелістер, сымдағы электр тербелістері, біліктің айналмалы тербелістері, газдың тербелістері сияқты есептер әкеледі. Жазықтықтағы толқындық теңдеу

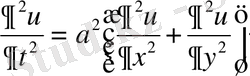
мысалы, мембрананың тербелісін сипаттайды. Ал

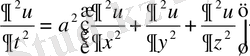
толқындық теңдеуі арқылы акустикалық тербелістер зерттеледі.

Толқындық теңдеулер гиперболалық түрдегі (типтегі) теңдеулерге жатады;

2) жылуөткізгіштік теңдеуі

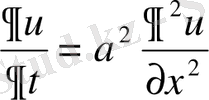
бұл түрдегі теңдеулерді зерттеуге жылудың таралуы, кеуекті ортада сұйық пен газды сүзу туралы есептер және ықтималдықтар теориясының кейбір есептері әкеледі.

Жылуөткізгіштік теңдеуі параболалық түрдегі (типті) теңдеулерге жатады;

  1. Лаплас теңдеуі

жазықтықтағы түрі - ;

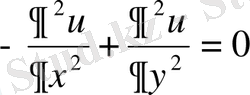кеңістікте - .

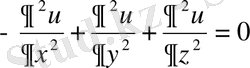Осындай теңдеулер көмегімен электр және магнит өрістерінің есептері, жылудың тұрақтылық күйі, гидродинамика, диффузия және серпімділік теориясының есептері зерттеледі.

Мұндай теңдеулер эллипстік түрдегі (типті) теңдеулерге жатады. Сонымен қатар, математикалық физиканың жиі қолданылатын кейбір теңдеулерін келтіруге болады;

4) Гельмгольц теңдеуі

,

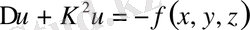бұл жиілігі берілген қалыптасқан периодты тербелістердің амплитудасының теңдеуі;

5) Шредингер теңдеуі

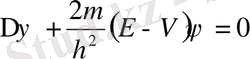- кванттық механиканың теңдеуі.

мұндағы 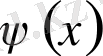-толқындық функция, -бөлшектің массасы, -бөлшектің энергиясы, 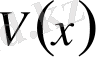-сыртқы күштер өрісінің потенциалы, 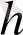-Планк тұрақтысы ;

6) телеграф теңдеуі

,

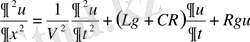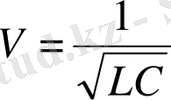
мұндағы 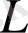-өздік индукция, -сиымдылық, 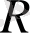-кедергі, -кернеу, 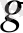-пропорционалдық коэффициент, 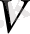-кабель бойынша берілген сигналдың жылдамдығы.


1. 2 Теңдеулерді түрлендіру және канондық түрге келтіру

Жоғарыдағы (1. 3) теңдеуге қайтып оралайық :

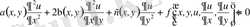
Бұл теңдеуді

,

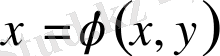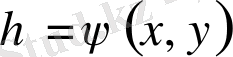
жаңа айнымалыларын пайдаланып берілген теңдеуге эквивалентті теңдеуге түрлендіруге болады.

Мұндағы 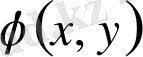және 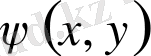- екі рет үздіксіз дифференциалданатын функциялар және түрлендіру анықтауышы (Якобиан) нөлден өзгеше, яғни

.

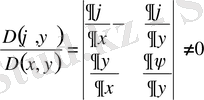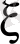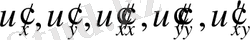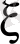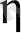Белгісіз u функциясының және жаңа айнымалылары бойынша дербес туындыларын ( 1. 3 ) теңдеуіне қойғанда тағы да бeлгісіз u функциясы мен жаңа және тәуелсіз айнымалыларының екінші ретті сызықтық теңдеуі алынады:

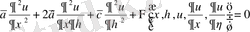
мұнда ,

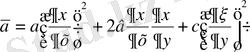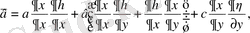
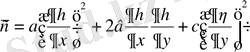
белгілеулері енгізілген, ал Ф функциясы 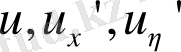бойынша сызықты функция болады. Бұл өрнектерден

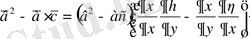
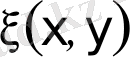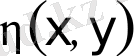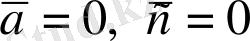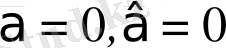екендігіне көз жеткізуге болады. Осыны ескере отырып, және функцияларын 1) 2) 3) 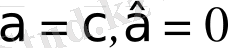шарттарының біреуі ғана орындалатындай етіп алса, онда (1. 3) теңдеуі қарапайым төрге келтіріледі.

Сонымен, (1. 3) теңдеуді қарапайым түрге келтіру үшін жаңа айнымалылардағы мен функцияларын

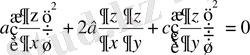
теңдеуінің шешімі болатындай етіп таңдап алу керек екендігі шығады. Ал бұл бірінші ретті сызықтық емес дербес туындылы теңдеу болып табылады. Осындай дербес туындылы теңдеудің шешімі мен қандай да бір жай дифференциалдық теңдеулер жүйесінің жалпы шешімі арасындағы байланыс туралы келесі теоремада айтылады.

Теорема . Берілген облыстың барлық нүктелерінде 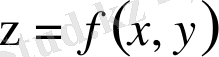функциясы

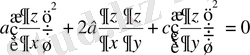
түріндегі дербес туындылы теңдеуді қанағаттандыруы үшін 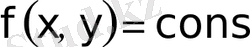функциялар жиыны

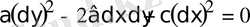
теңдеуінің жалпы интегралы болуы қажетті және жеткілікті. Осыдан, берілген теңдеуді қарапайым түрге келтіру үшін көмекші

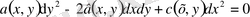(1. 5)

теңдеуін құру керек.

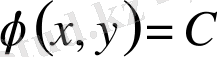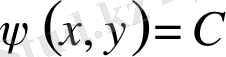Бұл теңдеу (1. 3) теңдеуінің сипаттамалық теңдеуі деп аталады. Ал оның және жалпы интегралдары теңдеудің сипаттауыштары деп аталады. Сипаттамалық (1. 5) теңдеуді екі теңдеу түрінде жазайық:

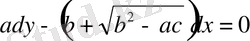
және

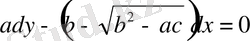
немесе,

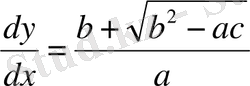(1. 6)

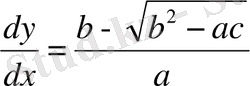(1. 7)

Түбір астындағы өрнек (1. 3) теңдеудің қай түрге жататындығын анықтауға мүмкіндік береді.

Егер қарастырылып отырған облыстың 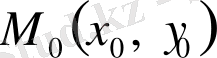нүктесінде

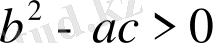болса, онда (1. 3) теңдеу гиперболалық типті,

болса, параболалық типті,

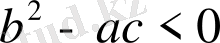болса, эллипстік типті теңдеуге жатады.

Екінші ретті дербес туындылы сызықтық теңдеулердің сипаттауыштары оларды канондық түрге келтіруге пайдаланылады.

1. 3 Канондық түрге келтіру әдісі сипаттауыштар әдісі

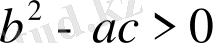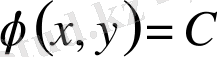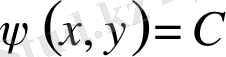1 Гиперболалық типті теңдеу үшін , ал (1. 6) және (1. 7 ) теңдеулерінің оң жақтары нақты және әртүрлі болады. Олардың және жалпы интегралдары сипаттауыштардың нақты жиынын анықтайды.

Енді

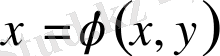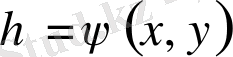, (1. 8)

деп алып (1. 3) теңдеуді мынадай канондық түрге келтіреміз

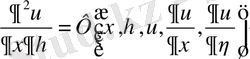(1. 9)

Егер 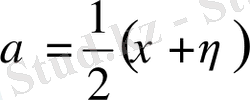, 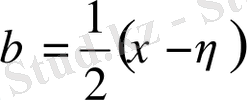деп алатын болсақ, онда

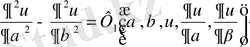(1. 10)

түріндегі канондық теңдеу алынады.

  1. Параболалық типті теңдеулерүшінболады да (1. 6) және (1. 7) теңдеулер бірдей бір теңдеуге айналады. Оның бір ғанажалпы интегралы болады. тәуелсіз болатындай етіп

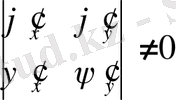
шарты бойынша алады .

Сонда 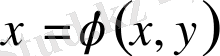және 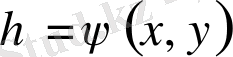арқылы түрлендіріп (1. 3) теңдеуді мынандай канондық түрге келтіреміз:

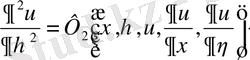(1. 11)

3 Эллипстік типті теңдеулер үшін 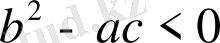болғандықтан, сипаттамалық теңдеудің түбірлері комплекс - түйіндес болады.

Бұл жағдайда жалпы интеграл

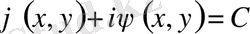
түрінде алынады. Сонда

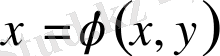, ал 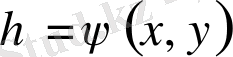деп алғанда (1. 3) теңдеу

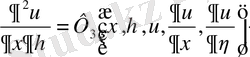
түріне келтіріледі.

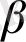Енді жаңадан және айнымалыларын

,

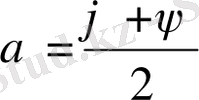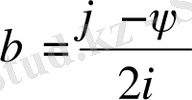
теңдіктері арқылы енгізейік. Онда 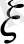мен 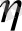айнымалылары

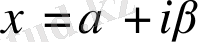және

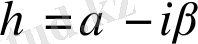
теңдіктерімен анықталады. Осы айнымалылар арқылы түрлендірулерден кейін

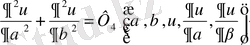(1. 12)

түріндегі эллипстік типті теңдеудің канондық түрін аламыз.

Жоғарыда қарастырылған (1. 3) теңдеуді (1. 9) -(1. 12) канондық түрге келтіру әдісі сипаттауыштар әдісі деп аталады.

2 Практикалық бөлім

2. 1 Есептерді шығару мысалдары

1-есеп.

Дербес туындылы

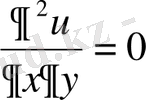(1. 13)

теңдеуінің жалпы шешімін табу керек .

Шешуі Берілген теңдеуді

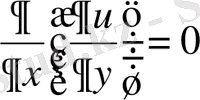
түрінде жазайық. Осыдан 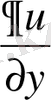туындысының 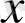бойынша туындысы нөлге тең болғандықтан ол 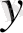ке тәуелді функция екендігі шығады, яғни

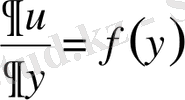
сондықтан .

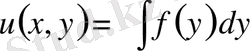Мұндағы кез келген 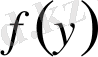функциясының интегралы 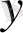-ке тәуелді 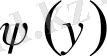функциясы мен тұрақты деп саналатын кез келген 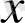-ке тәуелді 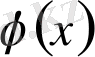функциясының қосындысынан тұрады.

Сонымен берілген теңдеудің жалпы интегралы

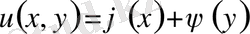(1. 14)

2-есеп.

Екінші ретті

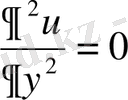(1. 15)

теңдеуінің жалпы шешімін табу керек.

Шешуі Теңдеуді

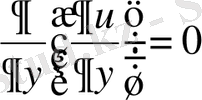
түрінде жазайық. Сонда 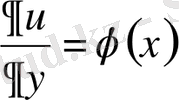, яғни ол тен тәуелсіз функция екендігі көрінеді.

Интегралдаудан кейін u ( x , y ) = ∫ φ ( x ) ∂ y + ψ ( x ) u(x, y) = \int_{}^{}{\varphi(x) \partial y + \psi(x) } , яғни

u ( x , y ) = y φ ( x ) + ψ ( x ) u(x, y) = y\varphi(x) + \psi(x) (1. 16)

шешімін аламыз.

3-есеп.

Берілген

0

y

u

6

x

u

2

y

u

3

y

x

u

4

x

u

2

2

2

2

2

=

∂

∂

+

∂

∂

∂

∂

+

∂

∂

∂

-

∂

∂

теңдеуін канондық түрге келтіру керек.

Шешуі Бұл теңдеуде 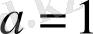, , 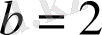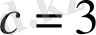болғандықтан

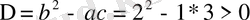
яғни теңдеу гиперболалық типке жатады. Сипаттамалық теңдеуі мына түрде жазылады 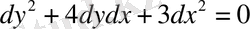, немесе 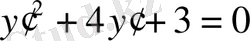. Оның түбірлері 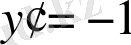, , 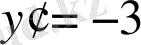болады да бірінші интегралдары (сипаттауыштары) , 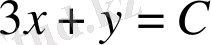түрінде алынады.

Теңдеуді канондық түрге келтіру үшін жаңа айнымалылар енгіземіз

,

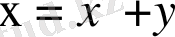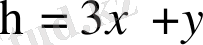
Теңдеуге қойып түрлендіру үшін осы айнымалылардың дербес туындыларын табайық.

Алдымен ескі айнымалылар бойынша туындыларды жаңа айнымалылар бойынша туындылармен өрнектеу формулаларын келтірейік.

Айталық,

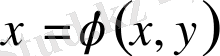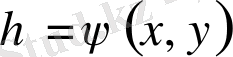, (1. 17)

екі рет үздіксіз дифференциалданатын функциялар болсын. Сонда төмендегідей туынды формулалары алынады:

; ;

;

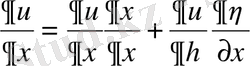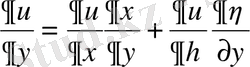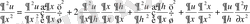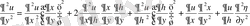
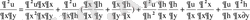
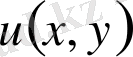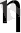Ескерту: функциясын жаңа және айнымалылармен өрнектеу формуласын қарастырайық

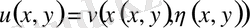(1. 19)

Әдетте (1. 18) формулаларда v-ның орнына u деп ауыстырып жазады. Бірақ та 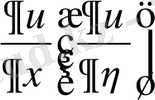туындыларын η=const (ξ =const) сызықтары бойынша алынған

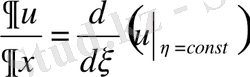
туындысы, ал дұрысында

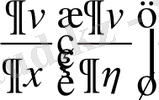
деп ұғу керек.

Өйткені « 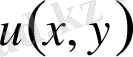функциясының 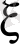немесе 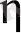бойынша дербес туындысы» дегеннің екінші 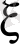немесе 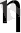координаты алынғанша мағынасы жоқ. . Шынында да, 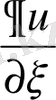туындысы 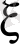айнымалысын ғана емес туындыда ашық көрінбесе де 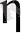айнымалысын таңдап алудан тәуелді.

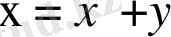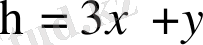Енді мысалымыздағы және жаңа айнымалылары бойынша дербес туындыларды есептейік:

, , ,

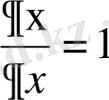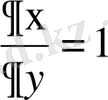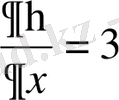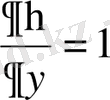
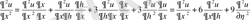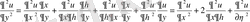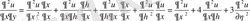
∂ u ∂ x = ∂ u ∂ ξ ∂ ξ ∂ x + ∂ u ∂ η ∂ η ∂ x = ∂ u ∂ ξ + 3 ∂ u ∂ η \frac{\partial u}{\partial x} = \frac{\partial u\partial\xi}{\partial\xi\partial x} + \frac{\partial u\partial\eta}{\partial\eta\partial x} = \frac{\partial u}{\partial\xi} + 3\frac{\partial u}{\partial\eta} ; ∂ u ∂ y = ∂ u ∂ ξ ∂ ξ ∂ y + ∂ u ∂ η ∂ η ∂ y = ∂ u ∂ ξ + ∂ u ∂ η \frac{\partial u}{\partial y} = \frac{\partial u\partial\xi}{\partial\xi\partial y} + \frac{\partial u\partial\eta}{\partial\eta\partial y} = \frac{\partial u}{\partial\xi} + \frac{\partial u}{\partial\eta}

;

;

Осыларды берілген теңдеуге апарып қоямыз:

Осыдан 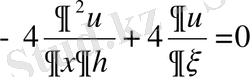, немесе 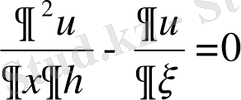- берілген теңдеудің канондық түрін аламыз.

4 есеп.

Берілген

4 ∂ 2 u ∂ x 2 + 4 ∂ 2 u ∂ x ∂ y + ∂ 2 u ∂ y 2 − 2 ∂ u ∂ y = 0 4\frac{\partial^{2}u}{\partial x^{2}} + 4\frac{\partial^{2}u}{\partial x\partial y} + \frac{\partial^{2}u}{\partial y^{2}} - 2\frac{\partial u}{\partial y} = 0

теңдеуін канондық түрге келтіру керек.

Шешуі: Бұл жағдайда a = 4 , b = − 2 , c = 1 a = 4, \ \ b = - 2, \ \ c = 1 және Δ = b 2 − a c = 2 2 − 4 • 1 = 0 \mathrm{\Delta} = b^{2} - ac = 2^{2} - 4 \bullet 1 = 0 болғандықтан, теңдеу параболалық типке жатады. Сипаттамалық теңдеуі 4 d y 2 − 4 d x d y + d x 2 = 0 4dy^{2} - 4dxdy + dx^{2} = 0 , немесе 2 d y − d x = 0 , d y = 1 2 d x , y = 1 2 x + C 2dy - dx = 0, \ dy = \frac{1}{2}dx, \ y = \frac{1}{2}x + C -бірінші интеграл. Сондықтан ξ = y − x 2 \xi = y - \frac{x}{2} деп аламыз. Ал екінші сипаттауыш үшін кез келген η = x \eta = x функциясын алуға болады. Өйткені бұл функциялардың Якобианы нөлге тең болмайды:

ξ x ′ ξ y ′ η x ′ η y ′ = − 1 2 1 1 0 = − 1 ≠ 0 \left \begin{matrix} \xi_{x}' & \xi_{y}' \\ \eta_{x}' & \eta_{y}' \end{matrix} \right = \left \begin{matrix} - \frac{1}{2} & 1 \\ 1 & 0 \end{matrix} \right = - 1 \neq 0

Сонымен ξ = y − x 2 \ \xi = y - \frac{x}{2} , η = x \ \eta = x жаңа айнымалылар бойынша дербес туындыларды есептейміз:

∂ ξ ∂ x = − 1 2 , ∂ ξ ∂ y = 1 , ∂ η ∂ x = 1 , ∂ η ∂ y = 0 \frac{\partial\xi}{\partial x} = - \frac{1}{2}, \ \frac{\partial\xi}{\partial y} = 1, \ \frac{\partial\eta}{\partial x} = 1, \ \frac{\partial\eta}{\partial y} = 0

∂ u ∂ x = ∂ u ∂ ξ ( − 1 2 ) + ∂ u ∂ η • 1 = − 1 2 ∂ u ∂ ξ + ∂ u ∂ η ; ∂ u ∂ y = ∂ u ∂ ξ • 1 + ∂ u ∂ η • 0 = ∂ u ∂ ξ ; \frac{\partial u}{\partial x} = \frac{\partial u}{\partial\xi}\left( - \frac{1}{2} \right) + \frac{\partial u}{\partial\eta} \bullet 1 = - \frac{1}{2}\frac{\partial u}{\partial\xi} + \frac{\partial u}{\partial\eta}; \ \frac{\partial u}{\partial y} = \frac{\partial u}{\partial\xi} \bullet 1 + \frac{\partial u}{\partial\eta} \bullet 0 = \frac{\partial u}{\partial\xi};

∂ 2 u ∂ x 2 = ∂ 2 u ∂ ξ 2 ( − 1 2 ) 2 − 1 2 ∂ 2 u ∂ ξ ∂ η + ∂ 2 u ∂ η ∂ ξ ( − 1 2 ) + ∂ 2 u ∂ η 2 • 1 = 1 4 ∂ 2 u ∂ ξ 2 − ∂ 2 u ∂ ξ ∂ η + ∂ 2 u ∂ η 2 \frac{\partial^{2}u}{\partial x^{2}} = \frac{\partial^{2}u}{\partial\xi^{2}}\left( - \frac{1}{2} \right) ^{2} - \frac{1}{2}\frac{\partial^{2}u}{\partial\xi\partial\eta} + \frac{\partial^{2}u}{\partial\eta\partial\xi}\left( - \frac{1}{2} \right) + \frac{\partial^{2}u}{\partial\eta^{2}} \bullet 1 = \frac{1}{4}\frac{\partial^{2}u}{\partial\xi^{2}} - \frac{\partial^{2}u}{\partial\xi\partial\eta} + \frac{\partial^{2}u}{\partial\eta^{2}}

∂ 2 u ∂ x 2 = ∂ 2 u ∂ ξ 2 ( − 1 2 ) 2 − 1 2 ∂ 2 u ∂ ξ ∂ η + ∂ 2 u ∂ η ∂ ξ ( − 1 2 ) + ∂ 2 u ∂ η 2 • 1 = 1 4 ∂ 2 u ∂ ξ 2 − ∂ 2 u ∂ ξ ∂ η + ∂ 2 u ∂ η 2 \frac{\partial^{2}u}{\partial x^{2}} = \frac{\partial^{2}u}{\partial\xi^{2}}\left( - \frac{1}{2} \right) ^{2} - \frac{1}{2}\frac{\partial^{2}u}{\partial\xi\partial\eta} + \frac{\partial^{2}u}{\partial\eta\partial\xi}\left( - \frac{1}{2} \right) + \frac{\partial^{2}u}{\partial\eta^{2}} \bullet 1 = \frac{1}{4}\frac{\partial^{2}u}{\partial\xi^{2}} - \frac{\partial^{2}u}{\partial\xi\partial\eta} + \frac{\partial^{2}u}{\partial\eta^{2}}

∂ 2 u ∂ y 2 = ∂ 2 u ∂ ξ 2 + ∂ 2 u ∂ η 2 • 0 + ∂ 2 u ∂ η ∂ ξ • 0 = + ∂ 2 u ∂ ξ 2 ; \frac{\partial^{2}u}{\partial y^{2}} = \frac{\partial^{2}u}{\partial\xi^{2}} + \frac{\partial^{2}u}{\partial\eta^{2}} \bullet 0 + \frac{\partial^{2}u}{\partial\eta\partial\xi} \bullet 0 = + \frac{\partial^{2}u}{\partial\xi^{2}};

∂ 2 u ∂ x ∂ y = ∂ 2 u ∂ ξ 2 ( − 1 2 ) + ∂ 2 u ∂ ξ ∂ η • 1 − 1 2 ∂ 2 u ∂ ξ 2 + ∂ 2 u ∂ ξ ∂ η \frac{\partial^{2}u}{\partial x\partial y} = \frac{\partial^{2}u}{\partial\xi^{2}}\left( - \frac{1}{2} \right) + \frac{\partial^{2}u}{\partial\xi\partial\eta} \bullet 1 - \frac{1}{2}\frac{\partial^{2}u}{\partial\xi^{2}} + \frac{\partial^{2}u}{\partial\xi\partial\eta}

Теңдеуге апарып қойып, оның канондық түрін табамыз:

4 ( 1 4 ∂ 2 u ∂ ξ 2 − ∂ 2 u ∂ ξ ∂ η + ∂ 2 u ∂ η 2 ) + 4 ( − 1 2 ∂ 2 u ∂ ξ 2 + ∂ 2 u ∂ ξ ∂ η ) + ∂ 2 u ∂ ξ 2 − 2 ∂ u ∂ ξ = 0 4\left( \frac{1}{4}\frac{\partial^{2}u}{\partial\xi^{2}} - \frac{\partial^{2}u}{\partial\xi\partial\eta} + \frac{\partial^{2}u}{\partial\eta^{2}} \right) + 4\left( - \frac{1}{2}\frac{\partial^{2}u}{\partial\xi^{2}} + \frac{\partial^{2}u}{\partial\xi\partial\eta} \right) + \frac{\partial^{2}u}{\partial\xi^{2}} - 2\frac{\partial u}{\partial\xi} = 0

немесе

4 ∂ 2 u ∂ η 2 − 2 ∂ u ∂ ξ = 0 4\frac{\partial^{2}u}{\partial\eta^{2}} - 2\frac{\partial u}{\partial\xi} = 0

Сонымен ∂ 2 u ∂ η 2 − 1 2 ∂ u ∂ η = 0 \frac{\partial^{2}u}{\partial\eta^{2}} - \frac{1}{2}\frac{\partial u}{\partial\eta} = 0 берілген теңдеудің канондық түрі.

5 есеп.

y 2 ∂ 2 u ∂ x 2 + x 2 ∂ 2 u ∂ y 2 − x 2 y ∂ u ∂ y − y 2 x ∂ u ∂ x = 0 y^{2}\frac{\partial^{2}u}{\partial x^{2}} + x^{2}\frac{\partial^{2}u}{\partial y^{2}} - \frac{x^{2}}{y}\frac{\partial u}{\partial y} - \frac{y^{2}}{x}\frac{\partial u}{\partial x} = 0

теңдеуінің типін анықтап, канондық түрге келтіру керек.

Шешуі: x=0 және y=0 түзулерінде жатпайтын нүктелерде болғандықтан, берілген теңдеу эллипстік типке жатады. Оның сипаттамалық теңдеуін құрайық

y 2 d y 2 + x 2 d x 2 = 0 y^{2}dy^{2} + x^{2}dx^{2} = 0

мұны екі теңдеу түрінде жазуға болады:

( y d y + i x d x ) ( y d y − i x d x ) = 0 (ydy + ixdx) (ydy - ixdx) = 0

Осыдан y 2 + i x 2 = C 1 y^{2} + ix^{2} = C_{1} және y 2 − i x 2 = C 2 y^{2} - ix^{2} = C_{2}\ екі бірінші интегралдарын аламыз. Сондықтан ξ = y 2 \xi = y^{2} және η = x 2 \eta = x^{2} деп алып, дербес туындыларды есептейміз.

ξ x ′ = 0 ξ y ′ = 2 y , η x ′ = 2 x , η y ′ = 0 \xi_{x}' = 0\ \ \xi_{y}' = 2y, \ \eta_{x}' = 2x, \eta_{y}' = 0

∂ u ∂ x = ∂ u ∂ ξ 0 + ∂ u ∂ η 2 x = 2 x ∂ u ∂ η ; ∂ u ∂ y = ∂ u ∂ ξ 2 y + ∂ u ∂ η • 0 = 2 y ∂ u ∂ ξ ; \frac{\partial u}{\partial x} = \frac{\partial u}{\partial\xi}0 + \frac{\partial u}{\partial\eta}2x = 2x\frac{\partial u}{\partial\eta}; \ \frac{\partial u}{\partial y} = \frac{\partial u}{\partial\xi}2y + \frac{\partial u}{\partial\eta} \bullet 0 = 2y\frac{\partial u}{\partial\xi};

∂ 2 u ∂ x 2 = ∂ 2 u ∂ η 2 ( 2 x ) 2 + 2 ∂ u ∂ η = 4 x 2 ∂ 2 u ∂ η 2 + 2 ∂ u ∂ η ; \frac{\partial^{2}u}{\partial x^{2}} = \frac{\partial^{2}u}{\partial\eta^{2}}(2x) ^{2} + 2\frac{\partial u}{\partial\eta} = 4x^{2}\frac{\partial^{2}u}{\partial\eta^{2}} + 2\frac{\partial u}{\partial\eta};

∂ 2 u ∂ y 2 = ∂ 2 u ∂ ξ 2 ( 2 y ) 2 + 2 ∂ u ∂ ξ = 4 y 2 ∂ 2 u ∂ ξ 2 + 2 ∂ u ∂ ξ ; \frac{\partial^{2}u}{\partial y^{2}} = \frac{\partial^{2}u}{\partial\xi^{2}}(2y) ^{2} + 2\frac{\partial u}{\partial\xi} = 4y^{2}\frac{\partial^{2}u}{\partial\xi^{2}} + 2\frac{\partial u}{\partial\xi};

∂ 2 u ∂ x ∂ y = 2 x ∂ 2 u ∂ η ∂ ξ 2 y = 4 x y ∂ 2 u ∂ ξ ∂ η \frac{\partial^{2}u}{\partial x\partial y} = 2x\frac{\partial^{2}u}{\partial\eta\partial\xi}2y = 4xy\frac{\partial^{2}u}{\partial\xi\partial\eta}

Осы мәндерді берілген теңдеуге қойып, оның канондық түріне келеміз

y 2 [ 4 x 2 ∂ 2 u ∂ η 2 + 2 ∂ u ∂ η ] + x 2 [ 4 y 2 ∂ 2 u ∂ ξ 2 + 2 ∂ u ∂ ξ ] − x 2 y • 2 y ∂ u ∂ ξ − y 2 x • 2 x ∂ u ∂ η = 0 , 4 x 2 y 2 ( ∂ 2 u ∂ η 2 + ∂ 2 u ∂ ξ 2 ) = 0 y^{2\ }\left\lbrack 4x^{2}\frac{\partial^{2}u}{\partial\eta^{2}} + 2\frac{\partial u}{\partial\eta} \right\rbrack + x^{2}\left\lbrack 4y^{2}\frac{\partial^{2}u}{\partial\xi^{2}} + 2\frac{\partial u}{\partial\xi} \right\rbrack - \frac{x^{2}}{y} \bullet 2y\frac{\partial u}{\partial\xi} - \frac{y^{2}}{x} \bullet 2x\frac{\partial u}{\partial\eta} = 0, \ \ 4x^{2}y^{2}\left( \frac{\partial^{2}u}{\partial\eta^{2}} + \frac{\partial^{2}u}{\partial\xi^{2}} \right) = 0 немесе 4 x 2 y 2 ≠ 0 4x^{2}y^{2} \neq 0 ге қысқартып:

∂ 2 u ∂ η 2 + ∂ 2 u ∂ ξ 2 = 0 \frac{\partial^{2}u}{\partial\eta^{2}} + \frac{\partial^{2}u}{\partial\xi^{2}} = 0

теңдеуін аламыз.

6 есеп.

Берілген

∂ 2 u ∂ x 2 − 2 s i n x ∂ 2 u ∂ x ∂ y − cos ⁡ 2 x ∂ 2 u ∂ y 2 − c o s x ∂ u ∂ y = 0 \frac{\partial^{2}u}{\partial x^{2}} - 2sinx\frac{\partial^{2}u}{\partial x\partial y} - \cos^{2}x\frac{\partial^{2}u}{{\partial y}^{2}} - cosx\frac{\partial u}{\partial y} = 0

теңдеуінің жалпы шешімін табу керек.

Шешуі: Бұл теңдеу үшін

b 2 − a c = 4 sin ⁡ 2 x − ( − cos ⁡ 2 x ) = 1 > 0 , b^{2} - ac = 4\sin^{2}x - \left( - \cos^{2}x \right) = 1 > 0,

яғни теңдеу гиперболалық типке жатады. Сипаттамалық теңдеуін жазайық:

d y 2 + 2 s i n x d x d y − cos ⁡ 2 x d x 2 = 0 dy^{2} + 2sinxdxdy - \cos^{2}xdx^{2} = 0

немесе

... жалғасы
Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.
Ұқсас жұмыстар
Математикалық физиканың дифференциалдық теңдеулерінің негізгі түрлері
Математикалық физика теңдеулері
ШЕКТЕЛГЕН СТЕРЖЕНЬДЕГІ ЖЫЛУ ӨТКІЗГІШТІК ТЕҢДЕУІНІҢ ҚОРЫТЫНДЫЛАУ ЖӘНЕ ОНЫ ФУРЬЕ ӘДІСІМЕН ИНТЕГРАЛДАУ
Бөлімдердің атаулары
Дербес туындылы сызықтық дифференциалдық теңдеулерді зерттеу
Екінші ретті дербес туындылы дифференциалдық теңдеулер
Эллиптикалық тектес теңдеулер
Статистикалық физика, термодинамика және физикалық кинетика негіздері
Рационал және иррационал теңдеулер мен теңсіздіктерді шешу әдістері
Жазықтықтағы аналитикалық геометрия
Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

google play appstore

instagram tiktok

Ақпарат

Қосымша


Email: info@stud.kz



Реферат Курстық жұмыс Диплом Материал Диссертация Практика Презентация Сабақ жоспары Мақал-мәтелдер 1‑10 бет 11‑20 бет 21‑30 бет 31‑60 бет 61+ бет Негізгі Бет саны Қосымша Іздеу Ештеңе табылмады :( Соңғы қаралған жұмыстар Қаралған жұмыстар табылмады Тапсырыс Антиплагиат Қаралған жұмыстар kz