Математиканың элективті курстарын ұйымдастыру

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 58 бет
Таңдаулыға:

МАЗМҰНЫ

КІРІСПЕ . . .

КІРІСПЕ . . .: 1

: ОРТА МЕКТЕПТЕ ЭЛЕКТИВТІ КУРСТАРДЫ ҰЙЫМДАСТЫРУ МӘСЕЛЕЛЕРІ

КІРІСПЕ . . .: 1. 1

: Орта мектеп математикасындағы элективті курстың маңызы: типтері, мақсаты, міндеттері мен қызметтері . . .

КІРІСПЕ . . .: 1. 2

: Мектеп математика курсында алтын қима элементтері кездесетін бөлімдер . . .

КІРІСПЕ . . .: 2

: ЖОҒАРЫ СЫНЫП ОҚУШЫЛАРЫНА АРНАЛҒАН «ГЕОМЕТРИЯДАҒЫ, ТАБИҒАТТАҒЫ ЖӘНЕ ӨНЕРДЕГІ АЛТЫН ҚИМА» ЭЛЕКТИВТІ КУРСЫН ӘЗІРЛЕУ . . .

КІРІСПЕ . . .: 2. 1

: Түсіндірме хат . . .

КІРІСПЕ . . .: 2. 2

: «Геометриядағы, табиғаттағы және өнердегі алтын қима» тақырыбындағы эллективті курстың оқу-тақырыптық жоспары

КІРІСПЕ . . .: ҚОРЫТЫНДЫ . . .

КІРІСПЕ . . .: ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ . . .

КІРІСПЕ

Жұмыстың өзектілігі : ХХ-ХХІ ғасырлар тоғысында Қазақстанның білім беру саласының өзекті сұрақтарының бірі - оқытудың сапасын арттыру мақсатында білім беру саласында білім жүйесінің тұрақты механизмін қалыптастыру және білім беру жүйесін модернизациялау. Модернизациялаудың құрамды бір бөлігі ол бейіндік оқыту. Жоғары сыныпта бейінді оқытуды қалыптастыру мақсатында элективті курстар, ақпараттық жұмыстар жүргізу.

Бейіндік дайындық негізгі мектеп оқушыларын педагогикалық, психологиялық, ақпаратты және ұйымдастырушылық тұрғыдан қолдау арқылы жоғары сынып оқушыларының болашақта білімдерін жалғастыруда дұрыс жол таңдауға көмектеседі. Элективті курстар білім беру мекемелерінде жаңадан енгізілгендіктен оған қатысты нормативтік құжаттар және әдістемелік материалдар әлі де жеткіліксіз. Көптеген мұғалімдер мектепте бейіндік оқытудың мақсаттары мен міндеттері, оны іске асырудың түрлері мен әдістері туралы толық ақпаратпен қамтамасыз етілмеген; оқушыларға қызықты және пайдалы болатын элективті курстарды құра алмайды. Сондықтан қазіргі кезде элективті курстар бойынша ақпараттарды жүйелеу, және оны өткізудің әдістемелік ерекшеліктерін табу өзекті сұрақтар болып отыр.

Осыдан келіп Алтын қима тақырыбы бойынша элективті курсын жасау мақсаты туындады.

Жұмыстың мақсаты: жалпы білім беретін орта мектептің жоғары сыныптарына арналған «Геометриядағы, табиғаттағы және өнердегі алтын қима» элективті курсын жасау.

Жұмыстың міндеттері:

Элективті курстардың пайда болу және даму тарихымен танысу;
Элективті курстардың мазмұнына қойылатын талаптарды анықтау;
«Геометриядағы, табиғаттағы және өнердегі алтын қима»элективті курсының мазмұнын анықтау;
«Геометриядағы, табиғаттағы және өнердегі алтын қима»элективті курсы бойынша әдістемелік нұсқау жасау.

Жұмыстың нысаны: Геометрия, алгебра

Жұмыстың құрылымы: Дипломдық жұмыс кіріспеден, екі бөлімнен, қорытындыдан және пайдаланылған әдебиеттер тізімінен тұрады. Кіріспеде зерттеудің өзектілігі негізделген, оның негізгі сипаттамалары берілген. Бірінші бөлімде орта мектептің жоғары сыныптарына математикадан элективті курстарды өткізудің мақсаттары, мазмұнын іріктеу, элективті курстардың түрлері мен әдістері қарастырылған. Жоғары сынып оқушыларының психологиялық-педагогикалық ерекшеліктері анықталған. Екінші бөлімінде элективті курсқа түсінік хат жазылған. Берілген элективті курстың мазмұны қысқаша түрде баяндалған және сабақтардың конспектілері ұсынылған. Қорытындысында негізгі тұжырымдары мен нәтижелері көрсетілген.

ОРТА МЕКТЕПТЕ ЭЛЕКТИВТІ КУРСТАРДЫ ҰЙЫМДАСТЫРУ МӘСЕЛЕЛЕРІ

1. 1 Орта мектеп математикасындағы элективті курстың маңызы: типтері, мақсаты, міндеттері мен қызметтері

Қазіргі уақытта мектептегі математикадан білім беруді ұйымдастырудың негізгі ұстанымы - математиканы оқытуды дифференциялдау. Бірақ қазіргі кезде математика курсының мазмұны туындаған талаптарға сәйкес келмейді. Адамға қажетті білім көлемі күрт артып, сабаққа жұмсалған сағат саны азайды. Мектеп пәні ретінде математика оқушыларды өткен ғасырдың аралығында қалдырады және қазіргі заманғы ғылыми жетістіктерді өте аз енгізеді. Бағдарламаның талаптарын іске асырудың және бұрыннан бар мәселелерді шешудің бір жолы - мектепті арнайы білімге көшіру және математикаға элективті курстарды енгізу.

Элективті курс - жоғары сынып оқушылары үшін міндетті курс болып табылады, олар мектеп компоненті есебінен жүзеге асырылады. «electus» сөзі латын тілінен таңдамалы, таңдаулы деген мағынаны береді. Демек, оқу жоспарында «таңдаулы» деп аталатын кез-келген курс таңдалуы керек. Элективті курстар орта мектеп деңгейінде бейіндік білім беру жүйесінде маңызды рөл атқарады. Элективті курстар, ең алдымен, әрбір студенттің жеке білім беру мүдделерін, қажеттіліктері мен бейімділігін қанағаттандыруға байланысты. Дәл осылар жеке білім беру бағдарламаларының қалыптасуының маңызды құралы және сонымен қатар әрбір оқушының таңдауына тығыз байланысты, білім мазмұны олардың қызығушылығына, қабілеттеріне¸келесі өмірлік жоспарларына тәуелді.

Білім беру жүйесіндегі элективті курстардың бұл рөлі олардың функциялары мен міндеттерінің кең ауқымын анықтайды. Сонымен қатар, элективті курстар білім берудің ішкі мамандануына үлес қосуы керек, сондай-ақ, оқушылардың білім беру бағытын дамытуға мүмкіндік береді. Өйткені білім беру жүйесіндегі ең басты міндеттердің бірі - адамның дайындығына қайта бағыттау, өз қабілеттеріне және мүмкіндіктеріне сәйкес жеке даму траекториясын өз бетімен таңдап, жауапкершілікпен шешім қабылдауға және қазіргі өзгеретін әлемде тиімді жұмыс істеуге мүмкіндік береді.

Таңдау бойынша курстар ақпараттық бейімделуі және нақты бейінмен белсенді түрде байланысуы, оқу жағдайларын модельдеу және оған тән проблемалар болуы керек. Элективті курстар мектеп компоненті есебінен жүзеге асырылады және келесі мақсаттарға ие болады:

математика бойынша бірыңғай мемлекеттік емтихан тапсыру үшін базалық деңгейде жұмыс істеуге немесе қосымша дайындықтан өтуге мүмкіндік беретін ең төменгі жалпы білім беру деңгейінде оқитын математика пәнінің негізгі білім мазмұнын дамыту;
математика пәнінің бейіндік курсының мазмұнын қосу оны толығымен тереңдетуге мүмкіндік беретін жоғарғы құрылымы;
таңдалған бейіннен тыс, адам қызметінің түрлі салаларында оқушылардың түрлі білім беру мүдделеріне қанағаттанушылық;
математиканы терең зерттеу арқылы математикалық ойлауды дамыту, тұлғалық қасиеттерді тәрбиелеу.

Элективті курстар мектеп білімін жетілдіруде үлкен рөл атқарады. Олар жаңа мазмұнды іздестіруге және тәжірибелік тексеруге, оқытудың жаңа әдістеріне, сондай-ақ зерттелетін материалдардың көлемін және күрделілігін өзгертуге мүмкіндік береді. Яғни, элективті курстар математиканы негізгі пән ретінде зерттеуге мүмкіндік береді немесе ішкі міндетті пән ретінде оқуға және білім траекториясын құрайды.

Математикадағы элективті курстардың типологиясы

Зерттеу барысында жүргізген педагогикалық, әдістемелік әдебиеттерді талдау элективті курстардың бірнеше типологиясы бар екенін көрсетті:

І. Тапсырмалар бойынша:

Таңдау бойынша курстар бірқатар тапсырмаларды орындайды:

1. Оқушыға одан әрі оқу бағытын және онымен байланысты кәсіби қызметтің белгілі бір түрін таңдауға немесе бас тартуға жағдай жасау;

2. Мұқият зерттеу үшін білім беру саласын таңдаған жоғары сынып оқушысына онымен байланысты қызмет түрлерінің алуан түрлілігін көруге көмектесу;

3. Оқушыларға дәстүрлі білім беру бағдарламасында ұсынылмайтын білім саласына қызығушылығын қанағаттандыру;

4. Оқу материалдарының қосымша бөлімдерімен таныстыру.

II. Келесі типология шартты түрде «Заттпен байланыс орнату арқылы» белгіленуі мүмкін:

Сурет 1. 1 - Элективті курстың байланыс орнатуы

Сонымен, оқу жоспарына кірмейтін «Пәнмен байланыс» элективті курстары пәндік, пәнаралық, элективті пәндер болып бөлінеді.

III. Мазмұны бойынша:

Сурет 1. 2 - Мазмұны бойынша элективті курстың түрлері

Математиканың элективті курстарын ұйымдастыру

Қазіргі таңда орта мектептің 7-сыныбынан бастап элективті курстар өткізу ұсынылады. Оқушылар тобы параллель сыныптарда жасалады, сонымен қатар жүйелі түрде оқушылардың бірлескен топтарын құруға болады. Элективті курс табысты өту үшін мүмкін болса, оларды мектеп кестесіне қосу, сабақтардың үзілуіне жол бермеу керек. Элективті курстарды өткізу мұғалімдердің дайындық деңгейіне жоғары талап қояды. Көптеген жағдайларда жоғары және орта арнайы оқу орындарының оқытушылары элективті курстар өткізуге шақырылады. Математиканың 9-сыныпқа дейінгі элективті курсын таңдау және қатысу еркін, ал 10-11 сыныптарда курстарға қатысу міндетті. Оқушыларға талаптар мектепте оқытылатын кез-келген пән сияқты: сабаққа міндетті түрде қатысу, үй тапсырмалары, жинақылық, мектептегі тәртіп және т. б. қамтиды.

Элективті курстардың келесі түрлері мына міндеттерді шешеді:

1. Сынақ (олар белгілі бір қызметтегі адам жұмысына тән әрекеттермен танысуға бағытталған, факультативтік курстармен салыстыруға болады, танымал ғылыми әдебиеттерді, кәсіптік лицей оқулықтарын және т. б. пайдалануға болады) .

2. Бағыт-бағдар беру (мысалы, экономикалық бейінге арналған «процентке арналған есептер» элективті курсы) ; білім беруде белгілі ғылыми әдебиеттерді, кәсіптік білім беру оқулықтарын, мектеп оқулықтары үшін қосымша тарауларды, жоғары оқу орындарына арналған оқулықтарды және т. б. пайдалануға болады.

3. Ортақ мәдениет (мысалы, кез келген бейін үшін «Алтын қима», «Сәулет саласындағы қисық» элективті курсы) .

4. Тереңдететін (осы элективті курстарда қосымша секцияны тереңдетіп зерттеу жүргізіледі; білім беру үшін факультативтік курстарға арналған тақырыптар мен тапсырмаларды, мектеп оқулықтары үшін қосымша тарауларды, жоғары білім беруге дайындық бойынша оқу құралдарын және т. б. ) [1]

Элективті курстарға қойылатын талаптар:

Артықшылық (олардың көп болуы керек) ;
Қысқа мерзімділік (6-16 сағат) ;
Мазмұнның түпнұсқалығы, атауы;
Курс белгілі бір нәтижемен аяқталуы;
Стандартты емес;
Элективті курстар әдетте, авторлық сипатта болады.

Оқу жоспары - оқу курсының мақсат, мазмұн, ерекшеліктерінің нәтижелігін бағалайтын нормативтік құжат. Элективті курстардың құрылымдық элементтері:

Титулдық бет;
Түсіндірме хат;
Мазмұны;
Әдістемелік бөлім;
Қосымша;
Бағдарламаны сараптау

Титулдық бет.

Өкілетті орган, курстың тақырыбы, курсты кім жүргізетіндігі жазылады.

2. Түсіндірме хат

Бағдарламаның өзектілігі, бағдарламаның қажеттілігін негіздеу (зерттелетін компоненттің маңыздылығы, негізгі курста оқудың болмауы, жас ерекшелігі, ғылыммен байланысы және т. б. ) ;
Бағдарламаның мақсаттары мен міндеттері (қызығушылықты дамыту, мамандық таңдауға көмектесу және т. б. ), мақсат нәтижелі болуы керек (жоба құру және т. б. ) ;
Логиканың мазмұнын таңдау негіздемесі (бағдарлама элементтері бір-бірімен байланысты болу керек, мазмұны бөлектенуі керек) ;
Интерактивті және пәнаралық байланыстарды көрсету;
Уақытша және материалдық ресурстардың сипаттамасы (бағдарлама типтік жабдықты қарастырады, экскурсияны қажет етеді және т. б. ) ;

- Бағдарлама мәтініне техникалық нұсқаулар (барлығы үшін бір мәтін, жоғары деңгейдегілерге - басқа) ;

3. Мазмұны

- Тақырыптың аты, сағат көрсетіледі;

- Демонстрациялар, практикалық және экскурсиялар тізімі беріледі;

4. Әдістемелік бөлім

- Әдістемелік ұсыныстар;

- Оқыту нәтижесінде алынған білімдер мен дағдыларға қойылатын талаптар;

- Құзыретті дамыту;

- Бақылау формалары мен әдістері;

- Ұсынылған әдебиеттер тізімі.

5. Қосымша

- Тақырыптық жоспарлау;

- Дидактикалық материал;

- Электронды презентациялар мен дискеттер;

6. Бағдарламаны сараптау

Бағдарламаның сараптамасы мектеп әдістемелік кеңесінде жүзеге асырылады;

Элективті курстар математикалық үйірмелерді, факультативтерді жаңа мазмұнмен ғана емес, оны ашудың жаңа тәсілдермен толықтырады. Сондай-ақ, элективті курстар олимпиадаларға дайындау, университетке түсу және т. б. үлкен мүмкіндіктер береді.

Кез-келген элективті курстар осы курсқа сәйкес келетін белгілі бір тапсырмалар жиынтығынсыз мүмкін емес. Элективті курстың міндеттері оқушылардың ойлау мәдениетін дамытудың, математиканың практикалық қосымшаларында оқушылардың дағдыларын қалыптастырудың қажетті құралдары ретінде пайдаланылады.

Міндеттерді іріктеу үшін элективті курстың мазмұнын меңгеруге бағытталған келесі принциптер белгіленеді:

1. Сабақтастық принципі. Тапсырмалар математикадағы (тұжырым-дамалар, теоремалар, қызмет көрсету әдістері және т. б. ) оқыту мазмұны тапсырманың мазмұны бойынша «енгізілген» болғандықтан, сабақтастық байланыстарды орнатуға үлес қосатынын ескеріңіз. Тапсырмалардың көмегімен әртүрлі ұғымдар, пікірлер, түрлі тақырыптар мен пәндер мен математиканың негізгі курсы мен элективті курстар арасында өзара байланыс орнатылады.

2. Теорияның практикамен байланыс принципі. Оқу барысында тапсырмалар теорияны тәжірибемен байланыстыратын құрал ретінде әрекет етуі керек, ал тәжірибе білімнен алдын ала немесе оны сүйемелдеуі мүмкін және оны жасай алады.

3. Толықтыру принципі, яғни міндеттер тізбегінде математикалық идеяларды толығымен көрсетуге ұмтылу, сондай-ақ ғылымның түрлі салаларына (физика, экономика және т. б. ) қатысты мысалдар беру, пәнаралық байланыстарды орнату.

4. Қарама қайшылық принципі тапсырмаларды іріктеуде бастапқы кезеңде тапсырмалардың қарама-қарсы түрлерін қабылдау, сол тапсырмалардың қайталануын болдырмау үшін. Бұл жағдайда, тапсырма оң және теріс жауаптармен бірге болуы керек.

5. Ғылыми білім әдістерін меңгеру негізінен тапсырмаларды шешуде басты рөл болып табылады. Сондықтан тапсырмалар жүйесі эвристикалық әдістермен оқытуды қамтуы тиіс. Аудиторияда есптерді шешу барысында оқушыларға негізгі эвристикалық әдістерді үйрету ұсынылады. Математикалық оқыту тәсілдерін зерттеуде эвристикалық әдістердің арасында жиі кездесетіні: ұқсастық, индукция, модельдеу әдісі және т. б.

6. Зерттеу дағдыларын қалыптастыру қағидаты. Оқу зерттеу жұмыстары арқылы білім беру міндеттерін жүзеге асырумен байланысты, оқушыларға шығармашылық ізденістің өзіндік жаңа білімін ұсынатын танымдық қызмет түрін түсінеміз. Оқу зерттеу жұмыстары бірнеше негізгі кезеңдерден тұрады: 1. проблемалық есеп; 2. гипотеза; 3. гипотезаны дәлелдеу немесе жоққа шығару. Көбінесе оқу зерттеу жұмыстарындағы қиындықтар мұғалімнің өзінен қалыптасады. Гипотезаны дәлелдеу немесе жоққа шығару, әдетте, математикалық фактіге тиісті гипотезаны дәлелдеуге келеді.
оқушылардың өзіндік эвристикалық белсенділігі гипотезамен байланысты.
Оқу зерттеу жұмыстарында гипотезаны жасау ұқсастық, салыстыру, шектеулі жағдайларды зерттеу, байқау, түйсік, тәжірибесі мен қорытындысына негіздейді [2] .

Элективті курстар мектепте уақытпен жүзеге асырылатындықтан,
оқу орнының құрамдас бөлігіне енгізілгенін ескеріледі. Сондықтан элективті курстарға бөлінген уақыт ішінде жеке профильдердің шамамен оқыту бағдарламасы 10-11 сыныптардағы сабақтар оқу тәжірибесін, жобаларын және ғылыми-зерттеу жұмыстарын ұйымдастыруға арналған. Сонымен қатар, элективті курстың шеңберінде оқытуды ұйымдастыру сыныптың кем дегенде екі кіші топқа бөлінуін білдіреді.

Математикадан элективті курстың мазмұны

Элективті курстардың мазмұны мұғалім әзірлеген бағдарламамен анықталады және «Математикадағы таңдаулы сұрақтар», «Қолданбалы математика» және «Қызықты математика», «Экономикадағы математика» және т. б. секцияларды қарастырады.

Элективті курстар бойынша тарихи материалдар

Математиканың тарихына негізгі курстарға қарағанда (әсірісе гуманитарлық пәндерде) элективті курстарда көбірек көңіл аударуға болады.

«Комбинаториканың элементтері және ықтималдықтар теориясы» элективті курсында тарихтың рөлі өте үлкен. Статистикалық ақпаратты өңдеудің маңыздылығына (туу мен өлім статистикасы, сақтандыру компанияларының қызметі және т. б. ) ықтималдық теориясын дамытудың алғашқы әрекеті ретінде қоғам дамуының қажеттіліктерін көрсету, ықтималдық теориясының негізгі түсініктері болатын қарапайым математикалық модель ретінде құмар ойындардың рөліне назар аудару.

Элективті курстардың бағдарламасы көбінесе авторлық болып табылатындықтан, оны меңгеру үшін оқушыдан материалды тыңдау және қабылдау, конспекті оңай жасау, сонымен қатар қосымша әдебиеттерді қолдана білуді талап етеді. Екінші жағынан, элективті курстар өздігінен жұмыс істеу дағдыларын дамытады, сондықтан ғылыми-зерттеу жұмыстарын ұйымдастыруға ерекше назар аудару керек. Осы мақсатта бағдарламада түрлі семинарлар болуы тиіс:

ғылыми мәтінмен топтық жұмыс жасау, одан кейін негізгі түсініктерді анықтау, мәселені оқшаулау, зерттеудің мақсаттары мен міндеттерін анықтау үшін ұжымдық талдау жасау;
кітапханада жұмыс істеу, каталогтар арқылы берілген тақырып бойынша әдебиеттерді таңдау;
компьютерлік сыныпта жұмыс істеу, электронды энциклопедиялар мен анықтамалықтарды пайдалану, ақпаратты таңдау үшін интернет серверлерін пайдалану;
осы мәселе бойынша көпшілік алдында сөз сөйлеу.

Алтын қима немесе «керемет пропорцияны» ежелгі және орта ғасыр математиктері кесіндінің бөлігі деп атады, яғни кесіндінің ұзындығының оның үлкен бөлігінің ұзындығына қатынасы, үлкен бөліктің ұзындығының кішіге қатынасындай болады. Бұл қатынас тең немесе жуықтап 0, 618. болсын, яғни «алтын қиманың» кесіндісі.

(1. 1)

Сурет 1. 3 - «Алтын қиманың» кесіндісі

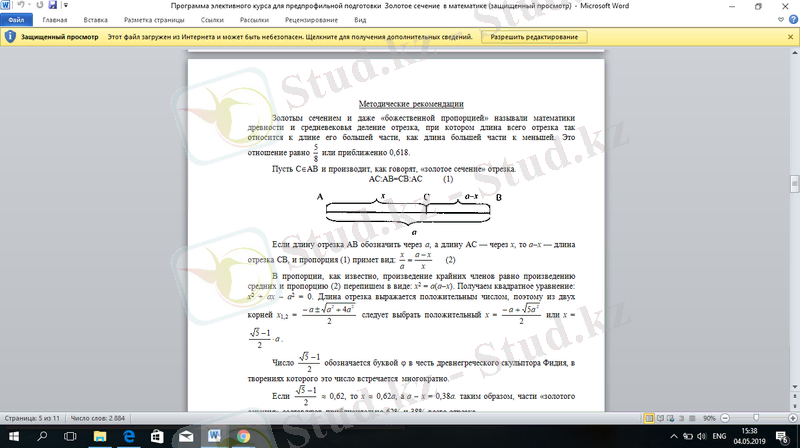
Егер АВ кесіндісін а арқылы белгілесек, АС кесіндісін х арқылы, сонда а- х - СВ кесіндісінің ұзындығы, және (1. 1) пропорция осындай түрге келеді:

(1. 2)

Пропорцияда, белгілі болғандай, шеткі мүшелерінің көбейтіндісі ортаңғы мүшелерінің көбейтіндісіне тең және (1. 2) пропорциясын мына түрде жазамыз: 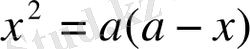. Квадраттық теңдеу аламыз: 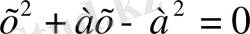. Кесіндінің ұзындығы оң сан болуы керек, сондықтан екі түбірден 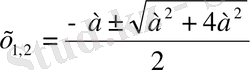оң мәнін ғана аламыз 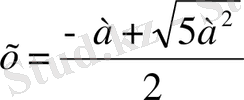немесе .

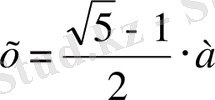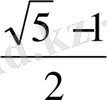саны ежелгі грек мүсіншісі Фидияның құрметіне $\varphi$ әріпімен белгіленеді, оның шығармаларында бұл сан жиі кездеседі. Егер 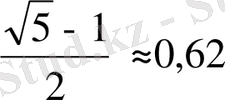, онда 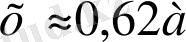, ал 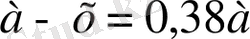осылай, кесіндінің «алтын қима» бөлігін шамамен 62% және 38% құрайды.

Сурет 1. 4 - Тікбұрышты үшбұрышта «алтын қиманы» тұрғызу

Геометриялық «алтын қиманы» келесі жолмен салуға болады: АВ кесіндісін салып, В нүктесінде АВ - ға перпендикуляр жүргіземіз, оған D нүктесін мына жолмен қоямыз, 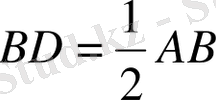болатындай. Ары қарай, А және D нүктелерін қосып, DЕ=AE аламыз. С нүктесі ізделінді, ол АВ кесіндісінде «алтын қима» жасайды. Негізінде Пифагор теоремасы бойынша 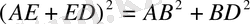екенін байқаймыз, ал салған кезде 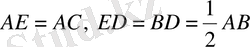. Бұл теңдеуден 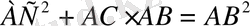, бұл жерден (1. 1) теңдеуді алу оңай.

1. 2 Мектеп математика курсында алтын қима элементтері

Жалпы білім беретін мекемелерге арналған авторлары В. Ф. Бутузов, С. Б. Кадомцев, В. В. Прасоловтың 8-сынып геометрия оқулығында 6 тарау: үшбұрыштады шешу тарауы, 16-параграф, 71-тақырыбында алтын қима элементтері туралы алғашқы ұғым беріледі. Кітапта төмендегідей қарастырылады.

АВ кесіндісін және онда жатқан М нүктесін қарастырайық. Егер 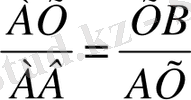(сурет 1. 5) болған жағдайда АМ және МВ кесінділері алтын қима құрайды делінеді, яғни кесіндінің үлкен бөлігінің жалпы кесіндіге қатынасы, кіші бөліктің үлкен бөлікке қатынасына тең.

Сурет 1. 5 - «Алтын қиманың» кесіндісі

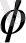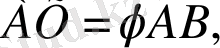
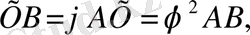
Бұл қатынаc гректің (фи) әріпімен белгіленеді. 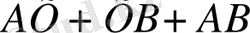болса, онда 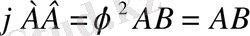, 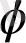үшін квадраттық теңдеу 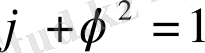орындалып, оның он түбірі 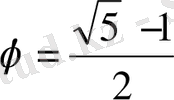тең болады.

Алтын қима сұлулық пен кемелдікке көп көңіл бөлген ежелгі гректерге де белгілі болатын. Олар бұл бөліктер алтын қима құраған жағдайда екі бөлікке бөлінген бөлікті көру ең жоғары үйлесім сезімін тудырадындығын дәлелдеді. Қайта өрлеу дәуірінде алтын қима тіпті «құдайдың пропорциясы» деп аталды. Тіптен алтын қима пропорцияларын адам денесінің құрылымынан да кездестіруге болады. Бұл бақылау түрі мүсіншілерде кеңінен қолданылады. Мысалға, атақты Аполлон Бельведерскийдің мүсінінде алтын қима элементтері көптеп кездеседі. Тіптен АМ:МВ қатынасын білдіретін 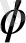әріпі де кездейсоқ бұлай аталмаған - бұл өзінің туындыларында алтын қиманы жүйелі түрде пайдаланған атақты ежелгі грек мүсіншісі Фидияның есімінің бірінші әріпі. Алтын қима архитектурада да жиі кездеседі.

Есеп. Берілген АВ кесіндісінде алтын қима тұрғызу.

Шешуі. В нүктесі арқылы АВ кесіндісіне (сурет 1. 6) перпендикуляр сәуле жүргіземіз және одан АВ -ның жартысына тең ВС кесіндісін аламыз. Содан кейін С центрі болатын ВС радиусымен шеңбер жүргіземіз және оның АС кесіндісімен қиылысу нүктесін D деп белгілейміз. М ізделінді нүктесі центрі А , АD радиусы болатын және АВ кесіндісінде шеңбердің қиылысу нүктесі болып табылады.

Негізінде, Пифогор теоремасы бойынша

Осы жерден 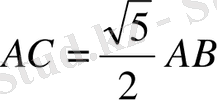, сондықтан

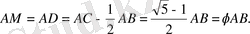
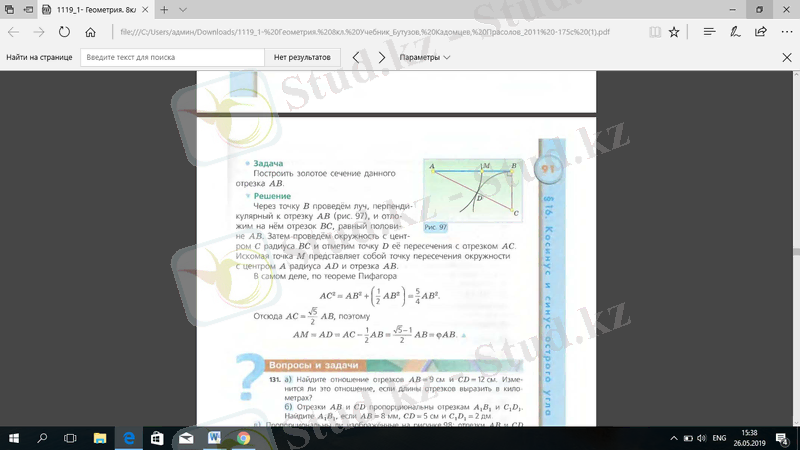
Сурет 1. 6 - АВ кесіндісінде алтын қима тұрғызу

Осылайша, элективті сабақтар оқушыларға әртүрлі қызығушылықтарды, ойлау мәдениетін, математикалық мәдениетті, білімін өз бетінше қалыптастыруға және дамытуға, оқушылардың тәуелсіз ғылыми-зерттеу жұмыстарын жүргізуге үйретуге және қазіргі заманның ғылыми жетістіктермен танысуға мүмкіндік береді. Бұдан басқа, олар оқушылардың ішкі әлеуетін ашуға, олардың өзін-өзі дамытуға жағдай жасайды. Элективті курс оқушының қабілетіне байланысты жеке қатынас жасау арқылы, олардың танымдық және өмірлік қызығушылықтарын толығымен қанағаттандырады. Элективті курстар Қазақстан, Ресей, Сингапур, Ұлыбритания, АҚШ және тағы басқа мемлекеттердің үздік білім орталықтары мен кәсіпорындарының базасында өткізіледі: Колмогоров ат. СУНЦ, Джонс Хопкинс Университеті Талантты Жастар Орталығы (CTY), The Bell Educational Services Ltd, International House Belfast Ltd, В. Н. Чаломей ат. Халықаралық ғарыш мектебі, FIF Technologies LLP, Ұлыбритания Корольдік институты, «Фитохимия» Халықаралық ғылыми-өндірістік холдинг» АҚ, Қазақ Ауыл шаруашылығы өнімін қайта өңдеу ғылыми-зерттеу институты.

2 ЖОҒАРЫ СЫНЫП ОҚУШЫЛАРЫНА АРНАЛҒАН «ГЕОМЕТРИЯ, ТАБИҒАТ ЖӘНЕ ӨНЕРДЕГІ АЛТЫН ҚИМА» ЭЛЛЕКТИВТІ КУРСЫН ӘЗІРЛЕУ

2. 1 Түсінік хат

«Геометриядағы, табиғаттағы және өнердегі алтын қима» элективті курсы оқушыларға табиғат пен өнердің осы феноменінің құрылымының негізіне қандай принциптер жатады деген сұрақты зерттеуге мүмкіндік береді.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.