МЕКТЕП МАТЕМАТИКА КУРСЫНДАҒЫ ЫҚТИМАЛДЫҚТАР ТЕОРИЯСЫ

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 67 бет
Таңдаулыға:

ДипломДЫҚ жұмыс
Тақырыбы: Ықтималдықтар теориясының олимпиадалық есептерін шешу әдістері

5В010900- Математика мамандығы бойынша

Орындаған: Дузелбаев M. C.

КІРІСПЕ

Тақырыптың өзектілігі. XXI ғасырда адамзат білім мен өнерде, техникалық прогресте үлкен жетістіктерге жетті. Бұның барлығында білімнің үлесі зор.
Еліміздің жаңаша дамуының шешуші факторы ретінде білім беру саласына қойылып отырған басты талап - әлемдік стандарттар деңгейіндегі сапалы білім беру қызметін көрсетуге қол жеткізу.
Білім алу саласында әрбір жеке тұлға өзінің белсенді, танымдық және шығармашылық іс-әрекеттерін дамытуы қажет. Оның айқын бір жолы - ғылыми шығармашылық ізденіс болып табылады.
Білім өркениеттіліктің әрі өлшемі, әрі тетігі болып табылатындықтан кез-келген мемлекеттің рухани және әлеуметтік дәрежесі білім деңгейіне байланысты бағаланады.
Республикамыздың білім беру жүйесінің даму бағытындағы негізгі мәселелердің бірі, уақыт талабына сай білім сапасын жақсарту, әлемдік стандарт деңгейіндегі білім беру болып табылады. Қазақстанның әлемдегі бәсекеге барынша қабілетті 50 елдің қатарына енуінің негізгі міндеті, жоғары мамандандырылған, білікті де білімді адамзат ғылыми технологияны оңай меңгеріп, нарықтық экономикада өзін-өзі басқара алатын және алған білімін өмірде пайдалана білетін болса, тек сол уақытта ғана жүзеге асыру мүмкін екендігі түсінікті.
Шынында да, әлемнің дамыған елдеріндегі білім беру жүйесі - білім дағдыларын механикалық түрде беру емес, ақпараттық зияткерлік ресурстарды өз беттерінше тауып, талдап және қолдана білетін, жедел өзгеріп отыратын техникалық прогресс, инновациялық өрлеу жағдайында өзін-өзі ашып көрсете алатын, нарықтық талап-талпыныстарға еркін бейімделе алатын жеке тұлғаны қалыптастыруға басымдық беретіндігі белгілі.
Бүгінгі таңдағы тәуелсіз мемлекетіміздің білім саласындағы басты мақсаты жан-жақты дамыған, шығармашылықпен жұмыс жасай білетін, өздігінен білім алу жолдарын таңдай алатын білімді де білікті жеке тұлға болу міндеті тұр. Кез-келген қоғамға дарынды адамдар керек, және қоғамның міндеті сондай адамдардың қабілетін дамыту. Өкінішке орай, кез-келген адам өз дарынын аша алмайды. Бәрі отбасына және мектепке байланысты. Отбасының міндеті баланың дарынын ертерек байқау болса, мектептің міндеті баланы қолдап, сол дарынын әрі қарай ашу, дамыту болып келеді. Әсіресе мектепте оқушының өзіндік шығармашылығының негізі қаланады. Кез-келген мұғалім мектеп оқулығын қызықсыз көріп, одан да терең ғылыми кітаптарды, энциклопедияларды оқитын, өздігінен ізденетін, әр түрлі салада өз сұрақтарына жауап іздейтін дарынды балаға жолығады. Сондықтан да оқушыға жол көрсету, оның өмірлік жоспарлары мен армандарына көмектесу мектепте жүзеге асу керек. Мұндай оқушыларды әр түрлі шығармашылық жұмыстармен, ғылыми жобалармен айналыстырып, олимпиадаларға, сайыстарға қатыстыру керек. Бұл оқушының жетістіктеріне басқалардың көз жұма қарамайтындығын, оған көңіл бөлетінін көрсетеді, осылайша оқушының қабілетін көрсетуге мүмкіндік туады. Оқушыларды жеке тұлға етіп тәрбиелеуде математика пәнінің де алатын орны, салмағы зор.
Мектептегі математика пәні мазмұнын жан-жақты зерттеп, орынды қолдану оқушылардың жалпы мәдени даму деңгейінің, білімінің жоғары болуына тікелей әсер ететіні сөзсіз.
Математика сабағында есеп шығару оқыту үрдісінің ең маңызды түрі болып табылады. Өйткені, есеп шығару арқылы оқушы математикалық теорияны меңгереді және логикалық ойлаумен шығармашылық қабілеті дамиды.
Мәселенің зерттелу деңгейі: Ықтималдықтар теориясының олимпиадалық есептерін шығару әдістері мен жолдары көптеген педагогтардың, ғалымдардың, әдіскерлердің: Олимпиадалық есептерді шығару әдістері мен жолдары көптеген педагогтардың, ғалымдардың, әдіскерлердің: Колмогоров А.Н., Шарыгин И.Ф., Гусев В.А., Агаханов Н.Х., Терешин Д.А., Фарков А.В., Галкин Е.В., Гальперин Г.А., Құрманалин Х.М., Күнғожин А.М., Байсалов Е.Р., Елеусізов Д.А., Ырысбек М., И.Р.Высоцкий, Ю.А.Цимбалов, И.Яковлев, И.В.Ященко еңбектерінде келтірілген. [4]
Алайда, ықтималдықтар теориясының олимпиадалық есептерін шығарылу жолдары жеткіліксіз зерттелгендігінен осы тақырып зерттеуге таңдалып алынды.
Бұл зерттеу жұмысымызда мектеп оқушыларының математикалық олимпиадаларында кездесетін ықтималдықтар теориясының олимпиадалық шешудің әртүрлі тәсілдері көрсетіледі.
Осы айтылғандар біздің зерттеу жұмысымыздың көкейкестілігін анықтап, зерттеу тақырыбын Ықтималдықтар теориясының олимпиадалық есептерін шешу әдістері - деп тұжырымдауға негіз болды.
Зерттеу мақсаты: математикалық олимпиадаларда кездесетін ықтималдықтар теориясының есептерін шешудің әдіс - тәсілдерін жүйелеп, сұрыптау және жиі қолданылатын негізгі тәсілдерін көрсету.
Зерттеу нысаны - орта мектептегі математика курсын оқыту үрдісі
Зерттеу пәні: оқулықтардағы және әр түрлі деңгейдегі математикалық олимпиадаларда кездесетін ықтималдықтар теориясы тақырыбына берілген есептер.
Зерттеу міндеттері:
а) зерттеу тақырыбы бойынша математикалық, әдістемелік әдебиеттерді оқып, танысу
ә) олимпиадаларда кездесетін ықтималдықтар теориясының есептерін шешудің тиімді әдіс - тәсілдерін талдап, жүйелеу
б) педагогикалық эксперимент бөлімінде болашақта Ықтималдықтар теориясы және математикалық статистика атты арнайы курс сабақтарында оқушыларды олимпиадаға дайындау мүмкіндіктерін көрсету.
Мәселенің деректік көзі: зерттеу проблемасы бойынша педагогтардың, математик - әдіскерлердің еңбектері, мектеп оқулықтары, математикалық олимпиадаға арналған әдістемелік әдебиеттер, математикалық интернет сайттар.
Зерттеудің әдістері, әдіснамалық негіздері: Математикалық олимпиадаларға арналған оқу-әдістемелік құралдарды оқу, зерттеу, жүйелеу және зерделеу, тәжірибелік-әдістемелік жұмыстарды жүргізу.
Зерттеудің жетекші идеясы: олимпиадалық есептерді шешуді үйрету арқылы оқушылардың ықтималдық теориясына қызығушылығы мен ынтасын арттырып, оқу сапасын жақсартуға болады.
Практикалық маңыздылығы: зерттеу нәтижелерін әдістемелік құралдарды дайындағанда, математиканы оқыту барысында оқушылардың ой-өрісін дамытуда, мектеп мұғалімдерінің білімін жетілдіру курстарында пайдалануға болады. Дайындалған арнайы курс жоспарын мектеп мұғалімдері өздерінің күнделікті іс-тәжірибелерінде қолдана алады.
Диплом жұмысының мақұлдануы. Диплом жұмысының негізгі мәселелері математика және математиканы оқыту әдістемесі кафедрасының отырысында тыңдалып, мақұлданды.
Диплом жұмысының құрылымы. Диплом жұмысы кіріспеден, екі тараудан, қорытындыдан, пайдаланылған әдебиеттер тізімінен тұрады.

1 МЕКТЕП МАТЕМАТИКА КУРСЫНДАҒЫ ЫҚТИМАЛДЫҚТАР ТЕОРИЯСЫ
1.1 Ықтималдықтар теориясының негізгі түсініктері және теоремалары
Ықтималдықтар теориясы өз бастауын XVII ғасырдан алады. Алдымен азартты ойындар пайда болды. Араб тілінде азар деген сөз қиын деген мағына береді. Арабтар азар деп лақтырылған ойын сүйегінің екеуінде де 6 ұпайдан түсүін айтады екен. Куб түріндегі ойын құралы ол кезде піл сүйегінен жасалатын болғандықтан ойын сүйегі деген атау сол заманнан қалыптасып қалған. Ықтималдықтар теориясы жөніндегі алғашқы жұмыстар XVII ғасырда басталды. Еуропа елдерінде адамды құнықтыратын әр түрлі ойындардың кең таралуына байланысты әр ойыншы өзінің жеңілмеу ықтималдықдығын алдын ала анықтауға тырысты. Сол кездегі математиктер де бұл мәселеге назар аудардып, бірнеше рет қайталанатын кездейсоқ оқиғалар туралы заңдылықтар ашуға талпынды. Бұл мәселеге алғашқы болып еңбектерін ұсынған: француз оқымыстысы Блез Паскаль, Пьер Ферма, голландиялық Христиан Гюйгенс, швецариялық математик Яков Бернулли болды. Француздың атақты математиктері Пьер Ферма мен Блез Паскальдың азартты ойындар жөніндегі зерттеулері ықтималдықтар теориясының негізін қалады. Кейіннен сақтандыру жұмыстарында және демография саласында ықтималдықтар теориясы өз қолданысын тапты. Жаратылыстану ғылымдары мен техниканың дамуы ықтималдықтар теориясына жаңа мәселелер қойды. Ықтималдықтар теориясының дамуын Бернулли, Муавр, ГауссЛаплас, Пуассон еңбектері көп әсер етті. XIX ғасырдың екінші жартысыннан бастап бұл саланың дамуына зор әсер еткен В.Я.Буняковский бастаған математиктер мектебі: П.Л.Чебышев, А.А.Марков, С.Н. Бернштейн, А.Н. Колмогоров секілді орыс ғалымдары үлкен үлес қосты. XVIII ғасыр аяғы мен XIX ғасыр басында ағылшын оқымыстысы А.Муавр, Л.Эйлер, Н.Бернулли, француз П.Лаплас, С.Пуассон, неміс К.Гаусс геодезия мен астраномияның өркендеуіне қатысты өлшеу қателіктерін бағалау, ату теориясындағы снарядтардың жағдайларын анықтау үшін ықтималдықтар теориясының рөлін көрсету мақсатында ғылыми жұмыстар жүргізді. XIX ғасыр ортасында Ф. Гальтон, Л.Больцман, А.Кетле, А.М.Ляпунов, П.Л.Чебышев, А.К.Калмогоров сияқты ғалымдар жиындар теориясы, шақты айнымалылы функциялар теориясы, функционалдық анализ сияқты жоғары математикалық жаңа табыстарына сүйенетін ықтималдықтар теориясының өркендеуіне негіз салды. Ықтималдықтар теориясының дамуына байланысты оның адамзат өмірінде қолдану мүмкіндігі артты. Жалпы алғанда ықтималдықтар теориясының әдісі ғылымның барлық саласына өз үлесін қосады. Ықтималдылық теориясы - математика тарауы, мұнда бір кездейсоқ оқиғаның берілген ықтималдықтары бойынша, қалай да болмасын алғашқымен байланысты болып келетін басқа кездейсоқ оқиғаның ықтималдығын табады. Ықтималдықтар теориясы құмар ойындар мен француз математигі және жазушысы Блез Паскальдің ол жөніндегі ойларының нәтижесінде пайда болды. Паскаль Ферм хаттарында ықтималдықтар теориясының негіздері алғаш рет баяндалған.
Ықтималдылық теориясының тамыры ғасырлар тереңінде жатыр. Көне Қытай,Индия, Египет, Грекия сияқты елдерде халық санағын жүргізу барысында, тіпті жауларының санын анықтау кезінде де ықтималдылық тұжырымдардың элементтері қолданылғандығы белгілі.Бірақ та бұл теорияның ғылым болып қалыптасуын XVII ғасырға жатқызады. біз тарихи романдардан білеміз, бұл корольдер мен мушкетерлердің, керемет ханымдар мен текті кавалерлердің кезеңі. Бір қызығы сол, осындай бір тарихи тұлғаның біреуінің есімімен осы ықтималдылық теориясының басталуы байланысты екен.
Математика - нақты ғылым,бір қарағанда кездейсоқтыққа ешқандай қатысы жоқ. Бірақ, осы кездейсоқтықтың сандық сипаттамасын, ықтималдық ұғымын берген басқа емес,осы математика. Ықтималдықтар теориясы өмірдегі кездейсоқтықтарды зерттеп, олардың заңдылықтарын ашады. Ықтималдықтар теориясының тарихына шолу Ықтималдықтар теориясы өз бастауын XVII ғасырдан алады.Алдымен азартты ойындар пайда болды.Араб тілінде азар деген сөз қиын деген мағына береді. Арабтар азар деп лақтырылған ойын сүйегінің екеуінде де 6 ұпайдан түсүін айтады екен. Куб түріндегі ойын құралы ол кезде піл сүйегінен жасалатын болғандықтан ойын сүйегі деген атау сол заманнан қалыптасып қалған.Ықтималдықтар теориясы жөніндегі алғашқы жұмыстар XVII ғасырда басталды. Еуропа елдерінде адамды құнықтыратын әр түрлі ойындардың кең таралуына байланысты әр ойыншы өзінің жеңілмеу ықтималдықдығын алдын ала анықтауға тырысты. Сол кездегі математиктер де бұл мәселеге назар аудардып,бірнеше рет қайталанатын кездейсоқ оқиғалар туралы заңдылықтар ашуға талпынды. Бұл мәселеге алғашқы болып еңбектерін ұсынған: француз оқымыстысы Блез Паскаль, Пьер Ферма,голландиялық Христиан Гюйгенс, швецариялық математик Яков Бернулли болды.
Француздың атақты математиктері Пьер Ферма мен Блез Паскальдың азартты ойындар жөніндегі зерттеулері ықтималдықтар теориясының негізін қалады. Кейіннен сақтандыру жұмыстарында және демография саласында ықтималдықтар теориясы өз қолданысын тапты. Жаратылыстану ғылымдары мен техниканың дамуы ықтималдықтар теориясына жаңа мәселелер қойды.
Ықтималдықтар теориясының дамуын Бернулли, Муавр, Гаусс, Лаплас,
Пуассон еңбектері көп әсер етті. XIX ғасырдың екінші жартысыннан бастап бұл саланың дамуына зор әсер еткен В.Я. Буняковский бастаған математиктер мектебі: П.Л.Чебышев, А.А.Марков, С.Н. Бернштейн, А.Н. Колмогоров секілді орыс ғалымдары үлкен үлес қосты. XVIII ғасыр аяғы мен XIX ғасыр басында ағылшын оқымыстысы А.Муавр,орыс оқымыстылары Л.Эйлер, Н.Бернулли, Д.Бернулли, француз П.Лаплас, С.Пуассон, неміс К.Гаусс геодезия мен астраномияның өркендеуіне қатысты өлшеу қателіктерін бағалау, ату теориясындағы снарядтардың жағдайларын анықтау үшін ықтималдықтар теориясының рөлін көрсету мақсатында ғылыми жұмыстар жүргізді.XIX ғасыр ортасында Ф.Гальтон, Л.Больцман, А.Кетле, А.М.Ляпунов, П.Л.Чебышев, А.К.Калмогоров сияқты оқымыстылар жиындар теориясы, шақты айнымалылы функциялар теориясы, функционалдық анализ сияқты жоғары математикалық жаңа табыстарына сүйенетін ықтималдықтар теориясының өркендеуіне негіз салды.

1.1.1 Ықтималдықтың классикалық, статистикалық, геометриялық анықтамалары

Ықтималдықтар теориясы тек кездейсоқ оқиғалар және олардың пайда болу мүмкіндіктерін қарастыратын математиканың бір бөлімі болып табылады. Сонымен қатар, ықтималдықтар теориясы қандай да бір оқиғаның шығуын алдын-ала анықтай алмайды, бірақ оның көмегімен көп рет қайталанған оқиғаның заңдылығын анықтауға болады. Оқиғалар 3 түрге бөлінеді: ақиқат, мүмкін емес және кездейсоқ.
Тәжірибе барысында міндетті түрде орындалатын оқиғаларды ақиқат оқиғалар деп атайды.
Тәжірибе кезінде пайда болмайтын оқиға мүмкін емес оқиға деп аталады.
Тәжірибе барысында орындалуы да, орындалмауы да мүмкін оқиға кездейсоқ деп аталады.
Оқиғалар латын алфавитінің бас әріптерімен A,B,C, ... арқылы белгіленеді.
Тәжірибе барысында екі оқиғаның бірі пайда болып, екіншісі пайда болмайтын оқиғалар үйлесімсіз деп аталады.
Тәжірибе кезінде мүмкін оқиғалардың әйтеуір біреуінің пайда болуы ақиқат болса, онда оқиғалар жалғыз мүмкіндікті оқиғалар деп аталады. Егер A,B,C,... оқиғалары жалғыз мүмкіндікті болса, онда олар толық топты құрайды.
Егер жалғыз мүмкіндікті екі оқиға толық топты құраса, онда олар қарама-қарсы оқиғалар деп аталады. A оқиғасына қарама-қарсы оқиғаны A деп белгіленеді.
Тәжірибе мен оқиға ұғымдарының айырмашылығын қарастырайық. Өмірде, тұрмыста, ғылымда жүргізілетін бақылаулар, сынақтар, экспери-менттерді тәжірибе деп атаймыз. Тәжірибенің нәтижесі оқиға болады.
1-мысал. Теңге бір рет лақтырылады. Бұл тәжірибе. Тәжірибенің нәтижесі оқиға болып есептеледі.
А оқиғасы - елтаңба жағының шығуы.
В оқиғасы-цифр жағының шығуы. Мұнда A және B үйлесімсіз (тоғыспайтын), қарама-қарсы оқиғалар және толық топ құрайды.
2-мысал. Жәшікте тек ақ шарлар бар. жәшіктен ақ шар алу - бұл ақиқат оқиға, ал жәшіктен қара шар алу - бұл мүмкін емес оқиға.
3-мысал. Жәшікте ақ, қара және қызыл шар бар. Бір шар алынады. Бұл тәжірибе болса, ал тәжірибенің нәтижесі мынадай оқиғалар болуы мүмкін.
А - ақ шар алынды.
В - қара шар алынды.
С - қызыл шар алынды.
Бұл оқиғалар үйлесімсіз оқиғалар және толық топ құрайды. Бірақ бұл оқиғалар қарама-қарсы оқиғалар бола алмайды. Қарама-қарсы оқиғаларда тек екі оқиға толық топ құрастырады. Ал біз қарастырып отырған жағдайда үш оқиға бар.
Мына мысалды қарастырайық. Жәшікте 6 стандартты және 4 стандартты емес зат бар. Жәшіктен бір зат алынған. Стандартты затты алу мүмкіндігі стандартты емес затты алуға қарағанда көп екені айқын. Бұл мүмкіндікті сипаттайтын сан ықтималдық деп аталады.
Анықтама. A оқиғасының ықтималдығы дегеніміз - осы оқиғаға қолайлы жағдайлар санының барлық жағдайлар санына қатынасы.
А оқиғасының ықтималдықтығы былай белгіленеді P(A). Сонымен,

P(A)=mn . (1.1)

Ықтималдықтың бұл анықтамасын классикалық анықтама немесе Лаплас моделі дейміз.Енді P(A) ықтималдығының қасиеттерін қарастырайық.
1. P(A) ықтималдығы теріс емес функция, яғни P(A)=0.
2. P(A) әрқашан 0=P(A)=1.
3. Қиылыспайтын (үйлесімсіз) A және B оқиғалары үшін, P(A+B) аддитивті функция, яғни PAB=PA+P(B).
Бұл үшінші қасиетті ықтималдықтарды қосу теоремасы немесе ықтималдықтарды қосу заң деп атайды.
Ықтималдықтың статистикалық анықтамасы. Қандай да бір оқиғаның ықтималдығын анықтау үшін оның орындалу жиілігін санау керек.
Жүргізілген n экспериментте берілген оқиға қанша рет орындалғанын абсолюттік жиілік көрсетеді.
Эксперименттің қандай үлесінде оқиғаның орындалғанын салыстырмалы жиілік не жиілік көрсетеді, ол абсолюттік жиіліктің эксперимент санына қатынасы.
ω=nm (1.2)

Оқиғаның орындалу жиілігі мен ықтималдығын ажырата білу керек. Ықтималдық туралы сөз болғанда n - барлық оқиғалар саны, m - қарастырып отырған оқиғаның орындалу саны. Ал жиілік жайлы айтылғанда, n - барлық жүргізілген тәжірибе саны, ал m - оқиғаның пайда болу саны.
Басқаша айтқанда оқиғаның жиілігі статистикалық ықтималдық деп аталады. Осы екі әр түрлі ұғымдардың тәуелділігі үлкен сандар заңы деп аталады. Мұнда кездейсоқ оқиғаның ықтималдығы ретінде көптеп жүргізілген тәжірибенің салыстырмалы жиілігін алуға болады. Тәжірибе неғұрлым көп жүргізілсе жиілігі бойынша оқиғаның ықтималдығын соғұрлым нақты анықтауға болады.
4-мысал. Ойын сүйегі 50 рет лақтырылды. Эксперименттің нәтижелерін кестеге енгізейік. Абсолюттік және салыстырмалы жиіліктерді есептейік.
Құрылған кестені пайдаланып абсолюттік және салыстырмалы жиіліктердің қасиеттерін анықтау керек.

1.1-Кесте. Ойын сүйегін лақтырғандағы нәтижелер

Шығу
Абсолюттік жиілік
Салыстырмалы жиілік
1 ұпай түсті
9
0,18
2 ұпай түсті
6
0,12
3 ұпай түсті
8
0,16
4 ұпай түсті
11
0,22
5 ұпай түсті
9
0,18
6 ұпай түсті
7
0,14
Эксперименттің барлық саны
50
1

1-қасиет. Абсолюттік жиіліктің қосындысы эксперимент санына тең.
2-қасиет. Салыстырмалы жиіліктің қосындысы 1-ге тең.
Ықтималдықтың геометриялық анықтамасы. Ықтималдықтар теориясының дамуының басында-ақ шектелген тең мүмкіндікті оқиғалар тобын құрастыруға негізделген ықтималдық теориясының класскалық анықтамасының жеткіліксіз болатыны ескерілген. Сол уақыттың өзінде-ақ жеке мысалдар қарастыру бұл анықтамаға біршама өзгерістер енгізіп оны ойша шектеусіз көп нәтижелер жағдайына лайықтап құру қажет болды. Мұнда да қайсыбір оқиғалардың тең мүмкінділігі түсінігі негізгі рөл атқарды.
Айталық жазықтықта қайсыбір G аймақ және тиісті шекарасы белгіленген g аймақ болсын. G аймаққа тәуекел деп лақтырылған нүктенің g аймаққа түсуінің ықтималдығы неге тең болады?
Лақтырылған нүкте G аймақтың кез келген нүктесіне түсуі мүмкін,ал осы аймақтың қандай да бір бөлігіне түсу ықтималдығы осы бөліктің өлшеміне пропорционал болады да оның орналасуына және түріне тәуелді болмайды.
Тәуекел деп лақтырылған нүктенің G аймақтың g бөлігіне түсу ықтималдығы деп Pg=m(g)m(G) қатынасын айтады.

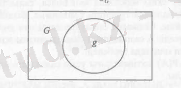
1-сурет
Анықтама. g облысына лақтырылған кездейсоқ нүктенің осы облысқа түсу ықтималдығы g өлшемнің G облыс өлшеміне қатынасына тең, яғни

Pg=g.өлшG.өлш . (1.3)

Мұнда да ықтималдықтың классикалық анықтамасы сияқты үш қасиет орын алады.
1. Pg теріс таңбалы емес, яғни Pg=0.
2. Ақиқат оқиға ықтималдығы бірге тең, яғни PG=1.
3. Қос-қостан үйлесімсіз оқиғалар қосындысының ықтималдығы олардың ықтималдықтарының қосындысына тең.
Геометриялық ықтималдықты анықтауға мысал қарастырайық.
5-мысал. Ұзындығы 20 см кесіндінің ішіне ұзындығы 10 см кіші кесінді орналастырылған. Үлкен кесіндіге кездейсоқ қойылған нүкте кіші кесіндіге түсетінің ықтималдығын тап. Нүктенің кесіндіге түсетінінің ықтималдығы кесіндінің ұзындығына пропорционал және оның орналасуына тәуелді емес.
Шешуі: Бұл есепті шығару үшін ықтималдықтың геометриялық анықтамасының формуласын қолданамыз. Мұнда үлкен кесіндінің ұзындығы L=20 см, ал осы ұзын кесіндінің ішінде жатқан кіші кесіндінің ұзындығы l=10 см. Формулаға сәйкес,
P=lL=1020=12 .
Жауабы: 12

1.1.2 Комбинаторика элементтері

Комбинаторика - берілген жиындағы элементтерден қандай да бір шартқа бағынатын әртүрлі қанша комбинация құрастыруға болады деген сұрақты қарастыратын математика саласын комбинаторика деп атайды.
Комбинаторика ұғымы XVI - ғасырда пайда болған. Ол кезде карта, сүйек ойыны, лотереялар сияқты құмарлық ойындар үлкен орын алған. Сондықтан алғашқыда комбинаторикалық есептер негізінен құмарлық ойындарға қатысты болған. Комбинаториканың дамуы Я.Бернулли, Лейбниц, Эйлер есімдерімен тығыз байланысты. Соңғы жылдары комбинаторика жедел даму үстінде. Комбинаторикалық әдістер транспорттық есептер шешуде, кестелер, өндірістік жоспарлар құрастыруда және өнімді өткізу мәселесінде қолданылады. Комбинаториканың негізгі ұғымдары көптеген ықтималдық есептерінің, сызықтық программалаудың, статистиканың негізі болып табылады. Сонымен қатар, комбинаторика автоматтар теориясында, экономикалық есептерде, биология және генетикада қолданылады.
Қандай да бір заттардан тұратын бір немесе бірнеше жиын берілсін. Осы заттардан, берілген шарттарды қанағаттандыратын комбинациялар құру талар етілсін. Мүмкін болатын барлық комбинациялар санын табу есептері, комбинаториканың есептері деп аталады. Ықтималдықтарды анықтауға қатысты көптеген есептерді шешкенде комбинаториканың формулаларын қолдану қажет болады. Сондықтан олардың төмендегі негізгі үш түріне тоқталамыз.
Алмастырулар. Бір-бірінен айырмашылығы тек элементтерінің орналасу ретінде ғана болатын комбинацияларды алмастырулар деп атайды.
Берілген n элементті қанша әдіспен осы n элементтердің қандай да бір тізбегі түрінде орналастыруға болады? Бұл сұраққа жауап беру үшін дербес жағдайлардан басталық. Әрбір элементті қазақ алфавитінің әріптерімен белгілейік. ә, у элементтері берілсе оларды әртүрлі ретпен орналастырып, әу және уә тізбектерін аламыз. Бұларды ә және у элементтерінен жасалған алмастырулар деп атайды. Демек, екі элементтен жасалған алмастырулар саны екіге тең. с,т,ү элементтері берілсін. Орналасу реттерін өзгертіп сүт, түс, үтс, стү, тсү, үст алмастыруларын аламыз, олардың саны 6-ға тең. е, к, ш, і элементтері берілсін. Төрт элементтен құралған алмастырулар санын табу үшін төмендегіше пайымдау жүргіземіз. Осы төрт элементтің кез келген біреуі алмастырудың бірінші орнында келуі мүмкін, ал қалған үшеуінен алты түрлі алмастыру құрылатынын көрдік. Сонымен, алмастырудың жалпы саны 6·4=24-ке тең болады, (ешкі,шекі,кеші,ішек,...). Бұл мысалдардан мынадай зандылықты байқауға болады: екі элементтен 2!=2 алмастыру, үш элементтен 3!=6 алмастыру, ал төрт элементтен 4!=24 алмастыруды құрастыруға болады екен.
Енді n-1 элементтен құралатын алмастырудың санын Pn-1- мен белгілейік те оны жоғарыдағы заңдылық бойынша Pn-1=n-1! түрінде жазалық. Онда берілген n элементтің кез келген біреуі, алмастырудың бірінші орнында келуі мүмкін, ал қалған n-1-інен құралған алмастырудың саны Pn-1=n-1!. Ендеше, берілген n элементтен құралған алмастырулар саны Pn=nn-1! . Бұл пайымдаулар n элементтен құралған алмастырулар санын беретін

Pn=n! (1.4)
формуланың дәлелдеуі болады.
2-анықтама. Егер алмастырудың бір немесе бірнеше элементтері, алмастыруда бірнеше рет қайталанатын болса, онда оны қайталамалы алмастырулар деп атайды.
1-мысал. "ана" сөзін беретін үш әріптен алты алмастыру құрауға болады: ана, наа, аан, ана, наа, аан. Бірақ, бұлардың соңғы үшеуі алдыңғы үшеуіне тең.
Үш элементтен бір элементі екі рет қайталанатын алмастырулар санын C3(2)-мен белгілейік.
C32=3!2!=3.
2-мысал. "анна" сөзін беретін төрт әріптен 24 алмастыру құрауға болады. Бірақ, мұндағы "н" және "а" әріптері екі реттен қайталанады. Сондықтан, 24 алмастырудың: нана, ннаа, наан, анна, анан, аанн алты алмастыруынан басқаларында осылар қайталанады. Төрт элементтен екеуі, екі реттен қайталанатын алмастырулар санын C42,2-мен белгілесе, онда:
C42,2=4!2!2!=6.
Орналастырулар. Берілген әртүрлі n элементтен m элемент бойынша орналасу деп бір-бірінен айырмашылығы не құрамында ,не орналасу ретінде не екеуінде де болатын комбинацияларды айтады. n элементтен m -нен жасалған орналастырулар саны Anm арқылы белгілеп, мына формуламен есептейді:
Anm=n!n-m! .
Мысал. 1, 2, 3, 4, 5 цифрлар арқылы цифрлары қайталанбайтын қанша а) екі таңбалы; б) үш таңбалы; в) төрт таңбалы; г) бес таңбалы сандар құрастыруға болады?
Шешуі: а) екі таңбалы сандар саны - 5 элементтен 2-ден алынған қайталанбайтын орналастырулар болады, онда формула бойынша:
A52=5!3!=1206=20.
б) үш таңбалы сандар саны - 5 элементтен 3-тен алынған қайталанбайтын орналастырулар болады, яғни формула бойынша
A53=5!2!=1202=60.
в) төрт таңбалы сандар саны - 5 элементтен 4-тен алынған қайталанбайтын орналастырулар
A54=5!1!=120.
г) бес таңбалы сандар саны да A54=5!1!=120 тең болады.
2-анықтама. Егер бір таңдамада бір элемент 2, 3, ...n рет қайталанса, онда оны n элементтен m элементті қайталанатын орналастырулар деп атайды. Оны былай белгілеп Anm, мынадай формула арқылы есептейді:

Anm=nm. (1.5)

1-мысал: 1, 2, 3, 4, 5 цифрлар арқылы цифрлары қайталанатын неше екі таңбалы, үш таңбалы, төрт таңбалы, бес таңбалы сандар құрастыруға болады.
Шешуі: Cанның цифрлары қайталанатын болғандықтан, екі таңбалы санның бірінші, екінші цифрын да бес әдіспен алуға болады. Онда көбейту ережес бойынша цифрлары қайталанатын екі таңбалы санды 25 әдіспен құрастыруға болады. Сондықтан формуласы бойынша:
A55=5∙5∙5∙5∙5=25.
Терулер. Берілген әртүрлі n элементтен m элемент бойынша терулер деп бір-бірінен айырмашылығы тек қана құрамында болатын комбинацияларды айтады.
n элементтен m-нен жасалған терулер саны Cnm арқылы белгіленеді. Терулер ұғымы орналастырулармен және алмастырулармен тығыз байланысқан. Шынында да, n элементтен m-нен жасалған орналастырудан айырмашылығы орналасу ретінде ғана болғандарын шығарып тастасақ, онда n элементтен m -нен жасалған терулер қалады, яғни Cnm=AnmPm . Керісінше егер әрбір теруде барлық мүмкін болған алмастыруларды орындап қоссақ, n элементтен m -нен жасалған барлық орналастырулар саны шығады, яғни

Anm=CnmPm. (1.6)
Сонымен,

Cnm=AnmPm=nn-1n-2∙... ∙[n-m-1]m!=n!n-m!m! . (1.7)

Терудің формуласы арқылы дәлелденетін екі қасиетін келітрейік:
1. Cnm=Cnn-m (симметриялық қасиеті);
2. Cn+1m=Cnm+Cnm+1 ( рекуренттік байланыс).
Мысал. Комиссия мүшелерін таңдау. Бөлімде 8 қызметкерлер бар, оның бесеуін интентарь есеп жүргізу комиссиясының мүшелері етіп жіберуге тиіс. Комиссияны қанша тәсілмен таңдауға болады?
Шешуі: Комиссияны таңдаудың тәсілдерінің саны 8 ден 5 элементтер бойынша терулердің санына тең, яғни:
C85=8∙7∙6∙5∙41∙2∙3∙4∙5=56.

1.1.3 Тәуелді және тәуелсіз оқиғалар
Ықтималдықтар теориясында оқиғаларды элементар оқиғаларға бөліп қана қоймай, оқиғалардың өқара тәуелділігі мен тәуелсіздігінің де жігін ажыратып қарастырады.
A оқиғасы B оқиғасынан тәуелсіз деген нені білдіреді? Егер A оқиғасының ықтималдығы пайда болғанына немесе пайда болмағанына қарай өзгермейтін болса, онда A оқиғасы B оқиғасынан тәуелсіз деп аталады. Басқаша айтқанда P(A) ықтималдығы A оқиғасының B оқиғасы орындалды деп есептегендегі ықтималдығы PAB-ға тең. Сондықтан,

PA=PAB=P(AB)P(B) (1.7)
яғни,
PA=P(AB)P(B),
осыдан,
PAB=PAPB.
Сонымен "A оқиғасы B-ден тәуелсіз" дегеніміз PA, PA, P(AB) ықтималдықтары үшін PAB=PAPB теңдігі орындалады дегенді білдіреді. Сонымен A оқиғасы A-ден тәуелсіз болса, онда симметриялы түрде A оқиғасыда B оқиғасынан тәуелсіз болады.
1-мысал. Екі тиын тасталды. Бірінішсінде "елтаңба" немесе "сан" жағының шығуы, екінші жағында " елтаңба" немесе "сан " жағының шығуына ешқандай әсер етпейді. Демек бірінші тиынның "елтаңба" жағының шығуы - A оқиғасы, екініш тиынның "елтаңба " жағының шығуы B-оқиғасынан тәуелсіз және керісінше, B оқиғасы A-оқиғасынан тәуелсіз, яғни A,B өзара тәуелсіз оқиғалар.
2-мысал. 36 карталық жиыннан бір карта таңдамай алынған. A - алынған картаның тұз болу оқиғасы, ал B-алынған картаның қызыл түсті болу оқиғасы. A және B оқиғалары өзара тәуелсіз.
PA=436=19; PB=1836=12 .
Егер A оқиғасының ықтималдығы B оқиғасының пайда болғанына немесе пайда болмағанына қарай өзгеретін болса, онда A оқиғасы B оқиғасына тәуелді деп аталды.
3-мысал. Кәсіпорынның жасайтын бұйымдарынан кез келген бір бұйым таңдамай алынған.А-алынған бұйым ақаусыз, В-алынған бұйым бірінші сортты. Онда B оқиғасы жүзеге асса, A оқиғасы міндетті түрде жүзеге асады. Сондай-ақ A оқиғасы жүзеге асса, B оқиғасы пайда болмайды. Демек A, B және A, B оқиғалары арасында тәуелділік байқалады.
4-мысал. Ойын сүйегі тасталды. A-жұп ұпайлардың шығу оқиғасы. B-үштен үлкен ұпайлардың шығу оқиғасы. Мұнда A және B оқиғаларының арaсында тәуелділік бар. A оқиғасы пайда болды деп, A-ның ықтималдылығын есептесек PA=23, егер ешбір қосымша мәліметсіз A оқиғасының ықтималдылығын есептесек: PA=36=0,5.

1.1.4 Шартты ықтималдық

Кез келген оқиға белгілі бір шарттар жиынтығы орындалғанда ғана пайда болуы немесе пайда болмауы мүмкін. Бірақ, кейбір жағдайларда, аталған шарттар жиынтығына қосымша, А оқиғасының пайда болу ықтималдығы басқа бір В оқиғасының пайда болғанына немесе болмағанына байланысты болатыны белгілі. Мұндай жағдайда А оқиғасы В оқиғасына тәуелді.
Көртеген жағдайларда кейбір оқиғалардың ықтималдықтарынан басқа басқа бір кезедейсоқ оқиғаның пайда болған.
Анықтама. A оқиғасының B оқиғасы пайда болды деген шарттағы ықтималдығы шартты ықтималдық деп аталады және ол былай белгіденеді: P(AB) немесе PB(A).
Айталық тәжірибе n рет жүргізілген болып олардан n1-інде B оқиғасы пайда болсын. Ал сол n1-дің m1-інде A оқиғасы пайда болсын. P(AB) ықтималдықты есептеу үшін n1 тәжірибе жүргізілген деп қабылдаймыз, себебі алғашқы шарттар жиынтығында B оқиғасы пайда болды деген шартқа қосылды, сондықтан n-нің ішіндегі B пайда болмаған жағдайды алып тастаймыз. Онда:
PAB=m1n1 . (1.8)
Шартты ықтималдық ұғымы тек тәуелді оқиғаларға ғана тән, егер екі оқиға тәуелсіз болса, онда олардың ықтималдықтары да бірін-бірі өзгертпейді, яғни
PBA=P(A) , PAB=P(B)
1-мысал. Бірінен кейін бірі екі тиын тасталды. A кемінде бір елтаңбаның шығу оқиғасы, B кемінде бір сан жағының шығу оқиғасы. Элементар оқиғалардың жалпы саны 4: EC,EE,CE,CC. A оқиғасының шартсыз ықтималдығы PA=34 ; ал A оқиғасының B оқиғасы пайда болды деген шарттағы ықтималдығы PAB=23 .
1.1.6 Толық ықтималдық формуласы
Күрделі оқиғалар ықтималдығын есептегенде ықтималдықтарды қосу, көбейту теоремаларын қолдануға тура келеді. Толық ықтималдық формуласы ықтималдықтарды қосу және көбейту теоремаларының салдары болып табылады. Осы формула әртүрлі жағдайда әртүрлі ықтималдықпен өтетін оқиғаның ықтималдығын анықтауға мүмкінлік береді, ал қарастырылған оқиғалардың пайда болуының шартты ықтималдықтары әрбір орындалатын жағдайларда белгілі болуы тиіс.
H1,H2,H3,...,Hn- оқиғалары қос-қостан үйлесімсіз және олардың бірігуі элементар оқиғалар кеңістігі Ω-ны құрайтын болсын. Hj-оқиғаларын гипотезалар (болжамдар) деп те атайды. Онда кез келген A оқиғасы Hj оқиғаларының біреуімен ғана бірігіп орындалады. Осы берілгендер бойынша

A=AH1+AH2+ ...+AHn. (1.9)
AHj оқиғалары да қос-қостан үйлесімсіз болғандықтан, олардың ықтималдықтарының қосындысы A-ның ықтималдығын береді:
PA=PAH1+PAH2+ ...+PAHn. (1.10)
Ал әрбір Hj үшін
PAHJ=PAHJPHJ. (1.11)
Сондықтан жоғарыдағы теңдікті былай жазамыз:
PA=PAH1PH1+PAH2PH2+ ...+PAHnPHn. (1.12)
Алынған теңдікті толық ықтималдық формуласы деп атайды.
1-мысал. Біркелкі үш типті 10 жәшік бар. Бірінші типтегі 4 жәшіктің әрқайсысында 25 жоғары сапалы, 15 сапалы бөлшек бар, екінші типтегі 3 жәшіктің әрқайсысында 22 жоғары сапалы және 8 сапалы бөлшек бар, үшінші типтегі 3 жәшіктің әрқайсысында 20 жоғары сапалы және 20 сапалы бөлшек бар. Бөлшек сапасын анықтау үшін кез келген жәшікті алып, одан кез келген бір бөлшек алады. Алынған бөлшектің жоғары сапалы болу ықтималдығын анықтау керек.
Шешуі: Алынған жоғары сапалы бөлшек A оқиғасы болсын. Жоғары сапалы бөлшек алу үшін алдымен 10 жәшіктің кез келген біреуін аламыз, ал бірінші типтегі жәшік (H1 оқиғасы), екінші типтегі жәшік (H2 оқиғасы), үшінші типтегі жәшік (H3 оқиғасы) болуы мүмкін. Мұндағы H1,H2,H3-гипотезалар болып табылады. Олардың сәйкесінше ықтималдықтары:
PH1=410=0,4,
PH2=310=0,3,
PH3=310=0,3.
Жоғары сапалы бөлшек пайда болуы, яғни A оқиғасының пайда болу ықтималдығы :
PAH1=2540=0,625,
PAH2=2230≈0,7,
PAH3=2040=0,5.
Сонда толық ықтималдық формуласы (1.12) бойынша :
PA=0,4∙0,25+0,3∙0,7+0,3∙0.5=0,61.
2-мысал. Ішіне шарлар салынған үш түрлі бірдей жәшікті алайық. Олардың біріншісінің ішінде 2 ақ және 1 қара шар, ал екіншісінде 3 ақ және 1 қара шар, ал үшіншісінде 2 ақ және 2 қара шар бар. Кез келген жәшіктің біреуін аламыз,ішінен кез келген бір шар аламыз, сол алынған шардың ақ болуының ықтималдығын табыңыз.
Шешуі: Айталық H1 оқиғасы бірінші жәшіктің, H2 оқиғасы екінші жәшіктің, H3 оқиғасы үшінші жәшіктің алынуы болсын. A оқиғасы алынған шардың ақ болу ықтималдығы. Есептің шарты бойынша H1,H2,H3 болжамдары тең мүмкіндікті оқиғалар болады:
PH1=PH2=PH3=13 .
Ал A оқиғасының шартты ықтималдығы толық ықтималдықтың формуласы бойынша
PA=13∙23+13∙14+13∙12=2336 .
Жауабы:

1.1.7 Бернулли формуласы
Саны n рет қайталанатын қандайда бір сынау жүргізілсін. Мұның әрқайсысында A оқиғасы пайда болуы да, пайда болмауы да мүмкін. Соның өзінде мына шарт орындалсын: әр сынауда A оқиғасының пайда болу ықтималдығы p=P(A) тұрақты, яғни ол не сынау ретінде, не алдыңғы сынаулар нәтижесіне тәуелді емес. Бұл шарт сынаулар тізбегі тәуелсіз екендігін көрсетеді. Осы шартты қанағаттандыратын сынаулар тізбегін тәуелсіз сынауларды қайталау схемасы немесе Бернулли схемасы деп атайды. Мұндай қарапайым схеманы тұңғыш құрастырған-Швецария ғалымы Я.Бернулли (1654-1705) еді. Ал сынауларды тәуелсіз дегенде біз оқиғаның пайда болу (болмау) ықтималдығы бір сынаудан екінші сынауға өткенде өзгермейді және оқиға басқа сынауларда пайда болды ма,не пайда болмады ма оған байланысты емес деп түсінетін боламыз. Бұл келтірілген мысалдарда сынау нәтижесі тек екі қарама-қарсы оқиғаның бірі ғана пайда болып, ал әрбір сынауда оқиғаның пайда болу ықтималдығы бірдей болады. Тәуелсіз сынаулардың мүмкіндік нәтижесі екіден артық және олардың ықтималдықтары әр түрлі болуы да мүмкін.
Теорема. Егер әрбір сынауда оқиғаның пайда болу ықтималдығы тұрақты p=P(A)- ға тең болса, онда n рет тәуелсіз сынау жүргізілгенде ол оқиғаның дәл m рет пайда болу ықтималдығы мына форомуламен анықталады
Pnm=Cnm∙pm∙qn-m (1.13)
Алынған формуланы Бернулли формуласы деп атайды. Осыдан n сынақта оқиғасының m1 және m2 аралығындаорындалу ықтималдығы
Pn(m1=m=m2=Pnm1+Pnm1+1+P2(m2) (1.14)
теңдігімен анықталады. Ал оқиғаның n сынақта кем дегенде бір рет орындалу ықтималдығы
Pnm=1=1-qn, q=1-p; (1.16)
формуласымен анықталады;
тәуелсіз n сынақтарда A оқиғасының m реттен кем пайда болуының ықтималдығы :
Pn0+Pn1+Pn2+ ...+Pnm-1; (1.17)
тәуелсіз n сынақтарда A оқиғасының m реттен артық пайда болуының ықтималдығы:
Pnm+1+Pnm+2+Pnm+3+ ...+Pnn; (1.18)
тәуелсіз n сынақтарда A оқиғасының кем дегенде m рет пайда болуының ықтималдығы:
Pnm+Pnm+1+Pnm+2+ ...+Pnn. (1.19)
1-мысал. Нысанаға 10 рет оқ атылды.Әрқайсысының нысанаға тию ықтималдығы 13-ке тең болса, онда атылған тәуелсіз 10 оқтың нақ төртеуінің нысанаға тию ықтималдығын табыңыздар.
Шешуі: Есеп шарты бойынша сынау саны n=10. Әрбір сынаудағы оқиғаның пайда болу ықтималдығы p=P(A)=13, q=23, m=4. Бернулли формуласына қойып есептесек,
Pnm=P104=C104∙134∙236=210∙134∙236=0 ,22760.
2-мысал. Нысанаға 6 рет оқ атылды. Әр атқан сайын нысанаға тию ықтималдығы 0,4-ке тең. Мына ықтималдықтарды табу керек.
a) нысанаға оқ бір рет дәл тиді;
б) нысанаға оқ тию саны 4-тен кем емес;
в) нысанаға ең болмағанда бір рет оқ тиді.
Шешуі: a) Бернулли формуласын пайдаланамыз. Есептің шарты бойынша n=6, m=1, p=0,4, q=1-0,4=0,6.
Сонда P61=C61∙p1∙q5=6∙0,4∙(0,6)5=0,1836.
б) нысанаға тиген оқ саны 4-тен кем емес оқиғасын A әрпімен белгілеп, 4, 5 және 6 рет тию ықтималдықтарын есептейміз
PA=P64+P65+P66≈0,1382+0,3686+0,0041 =0,5109 .
в) іздеп отырған оқиға ықтималдығын P(B) арқылы белгілеп, мынаны табамыз
PB=1-q6=1-0,66=1-0,0467=0,9533.

1.1.8 Кездейсоқ шама және оның сандық сипаттамалары
Ықтималдықтар теориясындағы негізгі ұғымдардың бірі кездейсоқ шамалар ұғымы. Бұл ұғымды түсіндіруді мысалдардан бастайық.
1-мысал. Ойын кубигін лақтырғанда ойын санының пайда болуын алдын ала айта алмаймыз. Бұл мысалда ұпай саны - кездейсоқ шама,куб жақтарының көрсететін 1,2,3,4,5,6 сандары-кездейсоқ шаманың қабылдайтын мүмкін мәндері.
2-мысал. Кез келген мақта қауашығында неше шит болуы мүмкін? Қауашақта неше шит болуын алдын ала айта алмаймыз, яғни бұл кездейсоқ шама. Ал қауашақтағы шит саны 1,2,3,4,...,n сол кезедйсоқ шаманың қабылдайтын мүмкін мәндері.
3мысал.Қоладағы лотореяның ұтыс мөлшерін білмейміз.Лотореяның ұтыс мөлшері-кездейсоқ шама, ал оның ұту мөлшерінің түрлі мәндері-сол кедейсоқ шама қабылдайтын мүмкін мәндері.
Анықтама. Сынау нәтижесінде қандай да бір мүмкін мәнді қабыдайтын шаманы кездейсоқ шама деп атайды.
Яғни кездейсоқ шама сан мәндерін қабылдайды. Бірақ дәл қандай мән қабылдайтынын алдын ала айта алмаймыз. Кездейсоқ шамаларды: X,Y,Z,..., арқылы бас әріптермен ал олардың қабылдайтын мәндерін x,y,z,..., кіші әріптермен белгілейміз. Қабылдайтын мәндер жиынына орай кездейсоқ шамаларды екі топқа бөледі: дискретті және үздіксіз.
0, 1, 2, ...,100 мүмкін мәндерінің біреуін қабылдайтын 100 жаңа туған нәрестелер ішіндегі ұл балалар саны, ойын сүйегін лақтырғанда түсетін ұпайлар саны т.с.с дискретті кездейсоқ шама болады.
Дискретті кездейсоқ шаманы сипаттау үшін, ең алдымен оның қабылдайтын мүмкін мәндерін, сонымен қатар бұл шаманың әр түрлі мәндерінің қаншалықты жиі кездесетінін білу керек. Бұл жиілік оның жеке мәндерінің ықтималдығын сипаттайды. Сонымен Х кездейсоқ шама мына x1,x2,...,xn мәндерінің біреуін қабылдайды, мұнда, x1x2...xn яғни X=xii=1,2,...,n теңдігімен өрнектелетін оқиға тәуелсіз және жалғыз мүмкіндікті болады. Сондықтан, p1+p2+...+pn=1.
Анықтама. Кездейсоқ шаманың мәндері мен осы мәндерді қабылдау ықтималдықтарының арасындағы байланысты орнататын қатынасты кездейсоқ шаманың үлестірім (таралу) заңы деп аталады.
Оны мынадай таблица арқылы береді.
1.2- Кесте. Кнздейсоқ шаманың үлестірімі

X
x1
x2
...
xk
P
p1
p2
...
pk

Кездейсоқ шамасының сандық сипаттамасы.
Дискретті кездейсоқ шаманың арифметикалық ортасы, таралу центрі немесе шашырау центрі деп аталатын сандық сипатын математикалық күтуі деп атайды.
Мүмкін мәндері x1,x2,...,xn болатын X - кездейсоқ шамасының сәйкес ықтималдықтары p1,p2,...,pn болсын.
Анықтама. Кездейсоқ дискретті X шамасының математикалық күтуі деп, оның барлық қабылдайтын мүмкін мәндері мен оларға сәйкес ыктималдықтарының көбейтіндісінің қосындысын айтады. X шамасының математикалық күтуі MX арқылы белгіленеді.

MX=x1p1+x2p2+ ... +xnpn. (1.20)

Егер дискретті кездейсоқ шаманың мүмкін мәндері шексіз болса, онда математикалық күту қатар болып табылады

MX=x1p1+x2p2+ ... +xnpn+ ...i=1infinityxipi (1.21)

1-қасиет. Тұрақты шаманың математикалық күтуі сол тұрақтының өзіне тең:
MC=0

2-қасиет. Тұрақты көбейткішті математикалық күту таңбасының алдына шығаруға болады:
MCX=CM(X)

3-қасиет. n кездейсоқ шаманың қосындысының математикалық күтуі осы шамалардың математикалық күтулерінің қосындысына тең:

MX1+X2+ ... +Xn=MX1+MX2+ ...+M(Xn)

4-қасиет. n кездейсоқ тәуелсіз шамалардың көбейтіндісінің математикалық күтуі осы шамалардың математикалық күтулерінің көбейтіндісіне тең

MX1∙X2∙ ... ∙Xn=MX1∙MX2∙...∙M(Xn)

1-мысал. Дискретті кездейсоқ шама X- бір ұтыс кұнының математикалық күтуін табу керек.
Шешуі: формуланы қолданамыз.

1.3-Кесте

X
5000
1000
500
200
100
0
P
0,002
0,01
0,025
0,1
0,15
0,713

MX=5000∙0,002+1000∙0,01+500∙0,025+2 00∙0,1+100∙0,15+0∙0,713=97,5 теңге.
Анықтама. Кездейсоқ шама мен оның математикалық күтуінің айырымының квадратының математикалық күтуін X кездейсоқ ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.